1、2020-2021 学年学年北京市东城区二校联考北京市东城区二校联考九年级上九年级上期中数学试卷期中数学试卷 一、选择题（本题共一、选择题（本题共 16 分，每小题分，每小题 2 分）分） 1下列图案中，是中心对称图形的是（ ） A B C D 2如图，点 A，B，C 在O 上，若AOB70，则ACB 的度数为（ ） A35 B40 C50 D70 3当 x0 时，函数 y的图象位于（ ） A第三象限 B第一、二、三象限 C第二、四象限 D第二象限 4将抛物线 y2x2向右平移 1 个单位，再向上平移 3 个单位，得到的抛物线是（ ） Ay2（x+1）2+3 By2（x1）2+3 Cy2（x+
2、1）23 Dy2（x1）23 5如图，O 的半径为 5，AB 为弦，OCAB，垂足为 E，如果 CE2，那么 AB 的长是（ ） A4 B8 C6 D10 6如图，PA、PB 是O 的切线，A、B 分别为切点，PO 交圆于点 C，若APB60，PC6，则 AC 的 长为（ ） A4 B C D 7如图，直线 y12x 和抛物线 y2x2+4x，当 y1y2时，x 的取值范围是（ ） A0 x2 Bx0 或 x2 Cx0 或 x4 D0 x4 8已知 O，如图， （1）作O 的直径 AB； （2）以点 A 为圆心，AO 长为半径画弧，交O 于 C，D 两点； （3）连接 CD 交 AB 于点 E
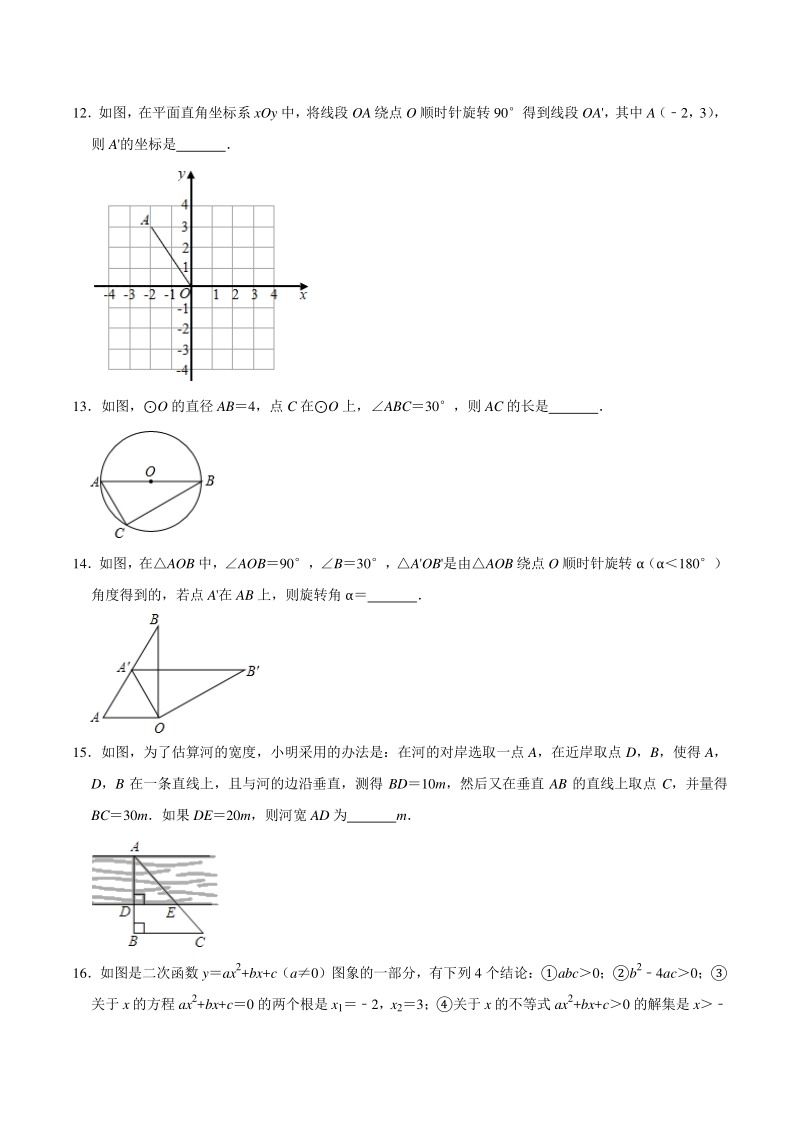
3、，连接 AC，BC 根据以上作图过程及所作图形，有下面三个推断： CEDE；BE3AE；BC2CE其中正确的推断的个数是（ ） A0 个 B1 个 C2 个 D3 个 二、填空题（本题共二、填空题（本题共 16 分，每小题分，每小题 2 分）分） 9在平面直角坐标系 xOy 中，点（4，5）关于原点的对称点坐标是 10已知在ABC 中，C90，AB6，BC5，则 sinA 11小云家开了一个小文具店，今年一月份的利润是 2250 元，三月份的利润是 1000 元，计算这个文具店 这两个月利润的平均下降率设这两个月利润的平均下降率为 x，则可列方程得 12如图，在平面直角坐标系 xOy 中，将线
4、段 OA 绕点 O 顺时针旋转 90得到线段 OA，其中 A（2，3） ， 则 A的坐标是 13如图，O 的直径 AB4，点 C 在O 上，ABC30，则 AC 的长是 14如图，在AOB 中，AOB90，B30，AOB是由AOB 绕点 O 顺时针旋转 （180） 角度得到的，若点 A在 AB 上，则旋转角 15如图，为了估算河的宽度，小明采用的办法是：在河的对岸选取一点 A，在近岸取点 D，B，使得 A， D，B 在一条直线上，且与河的边沿垂直，测得 BD10m，然后又在垂直 AB 的直线上取点 C，并量得 BC30m如果 DE20m，则河宽 AD 为 m 16如图是二次函数 yax2+bx
5、+c（a0）图象的一部分，有下列 4 个结论：abc0；b24ac0； 关于 x 的方程 ax2+bx+c0 的两个根是 x12，x23；关于 x 的不等式 ax2+bx+c0 的解集是 x 2其中正确的结论是 三、解答题（本题共三、解答题（本题共 68 分）分） 17 （5 分）解方程：2x23x20 18 （5 分）如图，AB 是O 的直径，弦 CDAB 于点 H，A30，CD4，求O 的半径的长 19 （5 分）如图，正方形 ABCD 的边长为 4，E 是 CD 中点，点 P 在射线 AB 上，过点 P 作线段 AE 的垂线 段，垂足为 F （1）求证：PAFAED； （2）连接 PE，
6、若存在点 P 使PEF 与AED 相似，直接写出 PA 的长 20 （5 分）二次函数 yax2+bx+c（a，b，c 是常数，a0）的自变量 x 与函数值 y 的部分对应值如下表： x 3 2 1 0 1 y ax2+bx+c 4 4 m 根据以上列表，回答下列问题： （1）直接写出 c，m 的值； （2）求此二次函数的解析式 21 （5 分）关于 x 的一元二次方程（k2）x24x+20 有两个不相等的实数根 （1）求 k 的取值范围； （2）如果符合条件的最大整数 k 是一元二次方程 k2+mk+10 的根，求 m 的值 22 （5 分）如图，在平面直角坐标系 xOy 中，直线 yx+3
7、 与函数 y（x0）的图象交于点 A（1，m） ， 与 x 轴交于点 B （1）求 m，k 的值； （2）过动点 P（0，n） （n0）作平行于 x 轴的直线，交函数 y（x0）的图象于点 C，交直线 y x+3 于点 D 当 n2 时，求线段 CD 的长； 若 CDOB，结合函数的图象，直接写出 n 的取值范围 23 （6 分）如图，在ABC 中，ABAC，以 AC 为直径的O 与 BC 交于点 D，DEAB，垂足为 E，ED 的延长线与 AC 的延长线交于点 F （1）求证：DE 是O 的切线； （2）若O 的半径为 2，BE1，求 CF 的长 24 （6 分）某超市销售一款洗手液，这款洗
8、手液成本价为每瓶 16 元，当销售单价定为每瓶 20 元时，每天 可售出 60 瓶市场调查反应：销售单价每上涨 1 元，则每天少售出 5 瓶若设这款洗手液的销售单价上 涨 x 元，每天的销售量利润为 y 元 （1）每天的销售量为 瓶，每瓶洗手液的利润是 元； （用含 x 的代数式表示） （2）若这款洗手液的日销售利润 y 达到 300 元，则销售单价应上涨多少元？ （3）当销售单价上涨多少元时，这款洗手液每天的销售利润 y 最大，最大利润为多少元？ 25 （6 分）有这样一个问题：探究函数 yx24|x|+3 的图象与性质 小丽根据学习函数的经验，对函数 yx24|x|+3 的图象与性质进行了
9、探究 下面是小丽的探究过程，请补充完整： （1）函数 yx24|x|+3 的自变量 x 的取值范围是 （2）如图，在平面直角坐标系 xOy 中，画出了函数 yx24|x|+3 的部分图象，用描点法将这个函数的 图象补充完整： （3）对于上面的函数 yx24|x|+3，下列四个结论： 函数图象关于 y 轴对称； 函数既有最大值，也有最小值； 当 x2 时，y 随 x 的增大而增大，当 x2 时，y 随 x 的增大而减小； 函数图象与 x 轴有 2 个公共点 所有正确结论的序号是 （4）结合函数图象，解决问题： 若关于 x 的方程 x24|x|+3k 有 4 个不相等的实数根，则 k 的取值范围是
10、 26 （6 分）在平面直角坐标系 xOy 中，抛物线 ymx2+2mx3 与 x 轴交于 A，B 两点（点 A 在点 B 左侧） ， 与 y 轴交于点 C，AB4 （1）直接写出抛物线的对称轴为直线 ，点 A 的坐标为 ； （2）求抛物线的解析式（化为一般式） ； （3）若将抛物线 ymx2+2mx3 沿 x 轴方向平移 n（n0）个单位长度，使得平移后的抛物线与线段 AC 恰有一个公共点，结合函数图象，回答下列问题： 若向左平移，则 n 的取值范围是 若向右平移，则 n 的取值范围是 27 （7 分）如图 1，ABC 和DEF 都是等腰直角三角形，A90，E90，DEF 的顶点 D 恰 好
11、落在ABC 的斜边 BC 中点，把DEF 绕点 D 旋转，始终保持线段 DE、DF 分别与线段 AB、AC 交于 M、N，连接 MN 在这个变化过程中，小明通过观察、度量，发现了一些特殊的数量关系 （1）于是他把DEF 旋转到特殊位置，验证自己的猜想如图 2，当 MNBC 时， 通过计算BMD 和NMD 的度数，得出BMD NMD（填，或） ； 设 BC2，通过计算 AM，MN，NC 的长度，其中 NC ，进而得出 AM、MN、NC 之间的 数量关系是 （2）在特殊位置验证猜想还不够，还需要在一般位置进行证明 请你对（1）中猜想的线段 AM、MN、NC 之间的数量关系进行证明 28 （7 分）
12、在平面直角坐标系 xOy 中，O 的半径为 1，对于O 和O 外的点 P，给出如下的定义：若在 O 上存在一点 Q，使得 P、Q 两点间的距离小于或等于 1，则称 P 为O 的近距点 （1）在点 P1（1，1） ，P2（，） ，P3（0，） ，P4（2，1）中，O 的近距点是 ； （2）若直线 l：yx+b 上存在O 的近距点，求 b 的取值范围； （3）若点 P 在直线 yx+1 上，且点 P 是O 的近距点，求点 P 横坐标 xP的取值范围 参考答案与试题解析参考答案与试题解析 一、选择题（本题共一、选择题（本题共 16 分，每小题分，每小题 2 分）分） 1下列图案中，是中心对称图形的是
13、（ ） A B C D 【分析】根据中心对称图形定义：把一个图形绕某一点旋转 180，如果旋转后的图形能够与原来的图 形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心进行分析即可 【解答】解：A、不是中心对称图形，故此选项不合题意； B、不是中心对称图形，故此选项不合题意； C、不是中心对称图形，故此选项不合题意； D、是中心对称图形，故此选项符合题意； 故选：D 2如图，点 A，B，C 在O 上，若AOB70，则ACB 的度数为（ ） A35 B40 C50 D70 【分析】直接根据圆周角定理即可得出结论 【解答】解：AOB70， ACBAOB35， 故选：A 3当 x0 时，函数
14、 y的图象位于（ ） A第三象限 B第一、二、三象限 C第二、四象限 D第二象限 【分析】先根据反比例函数的性质判断出函数 y的图象所在的象限，再根据各象限内点的坐标特点 判断出 x0 时函数图象所在的象限即可 【解答】解：反比例函数 y中 k50， 此函数的图象位于一、三象限， 当 x0 时函数的图象在第三象限 故选：A 4将抛物线 y2x2向右平移 1 个单位，再向上平移 3 个单位，得到的抛物线是（ ） Ay2（x+1）2+3 By2（x1）2+3 Cy2（x+1）23 Dy2（x1）23 【分析】易得原抛物线的顶点及平移后抛物线的顶点，根据平移不改变抛物线的二次项系数可得新的抛 物线解
15、析式 【解答】解：由题意得原抛物线的顶点为（0，0） ， 平移后抛物线的顶点为（1，3） ， 新抛物线解析式为 y2（x1）2+3， 故选：B 5如图，O 的半径为 5，AB 为弦，OCAB，垂足为 E，如果 CE2，那么 AB 的长是（ ） A4 B8 C6 D10 【分析】连接 OA，由于半径 OCAB，利用垂径定理可知 AB2AE，又 CE2，OC5，易求 OE，在 RtAOE 中利用勾股定理易求 AE，进而可求 AB 【解答】解：连接 OA， 半径 OCAB， AEBEAB， OC5，CE2， OE3， 在 RtAOE 中，AE4， AB2AE8， 故选：B 6如图，PA、PB 是O
16、的切线，A、B 分别为切点，PO 交圆于点 C，若APB60，PC6，则 AC 的 长为（ ） A4 B C D 【分析】如图，设 CP 交O 于点 D，连接 AD由切线的性质易证AOP 是含 30 度角的直角三角形， 所以该三角形的性质求得半径2；然后在等边AOD 中得到 ADOA2；最后通过解直角ACD 来求 AC 的长度 【解答】解：如图，设 CP 交O 于点 D，连接 AD设O 的半径为 r PA、PB 是O 的切线，APB60， OAAP，APOAPB30 OP2OA，AOP60， PC2OA+OC3r6，则 r2， 易证AOD 是等边三角形，则 ADOA2， 又CD 是直径， CA
17、D90， ACD30， ACADcot302 故选：C 7如图，直线 y12x 和抛物线 y2x2+4x，当 y1y2时，x 的取值范围是（ ） A0 x2 Bx0 或 x2 Cx0 或 x4 D0 x4 【分析】联立两函数解析式求出交点坐标，再根据函数图象写出抛物线在直线下方部分的 x 的取值范围 即可 【解答】解：由，解得或， 两函数图象交点坐标为（0，0） ， （2，4） ， 由图可知，y1y2时，x 的取值范围是 x0 或 x2 故选：B 8已知 O，如图， （1）作O 的直径 AB； （2）以点 A 为圆心，AO 长为半径画弧，交O 于 C，D 两点； （3）连接 CD 交 AB 于
18、点 E，连接 AC，BC 根据以上作图过程及所作图形，有下面三个推断： CEDE；BE3AE；BC2CE其中正确的推断的个数是（ ） A0 个 B1 个 C2 个 D3 个 【分析】连接 OC，根据作图过程可得，再根据垂径定理即可判断； 根据作图过程可得 ACOAOC，即AOC 是等边三角形，再根据等边三角形的性质即可判断； 可以根据直角三角形 30 度角所对直角边等于斜边的一半，也可以根据三角形相似对应边成比例得结 论 【解答】解：如图，连接 OC， AB 是O 的直径， ACB90， 以点 A 为圆心，AO 长为半径画弧，交O 于 C，D 两点， ， 根据垂径定理，得 ABCE，CEDE，
19、 所以正确； ACOAOC， AOC 是等边三角形， ABCE， AEOE， BEBO+OE3AE， 正确； 方法一： CAO60，ACB90，CBE30， BC2CE 所以正确 方法二： 由ACECBE， AC：AEBC：CE2：1， BC2CE， 所以正确， 故选：D 二、填空题（本题共二、填空题（本题共 16 分，每小题分，每小题 2 分）分） 9在平面直角坐标系 xOy 中，点（4，5）关于原点的对称点坐标是 （4，5） 【分析】利用关于原点对称点的坐标特点可得答案 【解答】解：点（4，5）关于原点的对称点坐标是（4，5） ， 故答案为： （4，5） 10已知在ABC 中，C90，AB
20、6，BC5，则 sinA 【分析】根据三角函数的定义解决问题即可 【解答】解：如图， C90，BC5，AB6， sinA 故答案为： 11小云家开了一个小文具店，今年一月份的利润是 2250 元，三月份的利润是 1000 元，计算这个文具店 这两个月利润的平均下降率 设这两个月利润的平均下降率为 x， 则可列方程得 2250 （1x） 21000 【分析】直接利用一元二次方程中下降率求法得出方程即可 【解答】解：设这两个月利润的平均下降率为 x，则可列方程得： 2250（1x）21000 故答案为：2250（1x）21000 12如图，在平面直角坐标系 xOy 中，将线段 OA 绕点 O 顺时
21、针旋转 90得到线段 OA，其中 A（2，3） ， 则 A的坐标是 （3，2） 【分析】根据题意画出图形，即可解决问题 【解答】解：如图，观察图象可知，A（3，2） 故答案为（3，2） 13如图，O 的直径 AB4，点 C 在O 上，ABC30，则 AC 的长是 2 【分析】根据圆周角定理得出ACB90，进而利用直角三角形中 30所对直角边等于斜边一半，求 出即可 【解答】解：直径 AB4， ACB90， 点 C 在O 上，ABC30， ACAB2， 故答案为：2 14如图，在AOB 中，AOB90，B30，AOB是由AOB 绕点 O 顺时针旋转 （180） 角度得到的，若点 A在 AB 上，
22、则旋转角 60 【分析】根据旋转的性质得出 OAOA，得出OAA是等边三角形则AOA60，则可得出 答案 【解答】解：AOB90，B30， A60 AOB是由AOB 绕点 O 顺时针旋转 角度得到的， OAOA OAA是等边三角形 AOA60，即旋转角 的大小是 60 故答案为：60 15如图，为了估算河的宽度，小明采用的办法是：在河的对岸选取一点 A，在近岸取点 D，B，使得 A， D，B 在一条直线上，且与河的边沿垂直，测得 BD10m，然后又在垂直 AB 的直线上取点 C，并量得 BC30m如果 DE20m，则河宽 AD 为 20 m 【分析】证出ADE 和ABC 相似，然后根据相似三角
23、形对应边成比例列式求解即可 【解答】解：ABDE，BCAB， DEBC， ADEABC， ，即， 解得：AD20m 故答案为：20 16如图是二次函数 yax2+bx+c（a0）图象的一部分，有下列 4 个结论：abc0；b24ac0； 关于 x 的方程 ax2+bx+c0 的两个根是 x12，x23；关于 x 的不等式 ax2+bx+c0 的解集是 x 2其中正确的结论是 【分析】根据抛物线开口方向，对称轴的位置以及与 y 轴的交点可对减小判断；利用抛物线与 x 轴的 交点个数可对进行判断；根据二次函数的性质可对进行判断；利用图象则可对进行判断 【解答】解：抛物线开口向下，交 y 轴的正半轴
24、， a0，c0， ， ba0， abc0，所以错误； 抛物线与 x 轴有 2 个交点， b24ac0， 即 b24ac，所以正确； 抛物线 yax2+bx+c 经过点（2，0） ， 而抛物线的对称轴为直线 x， 点（2，0）关于直线 x的对称点（3，0）在抛物线上， 关于 x 的一元二次方程 ax2+bx+c0 的两根是 x12，x23，所以正确 由图象可知当2x3 时，y0， 不等式 ax2+bx+c0 的解集是2x3，所以错误； 故答案为 三、解答题（本题共三、解答题（本题共 68 分）分） 17 （5 分）解方程：2x23x20 【分析】利用因式分解法把原方程化为 x20 或 2x+10
25、，然后解两个一次方程即可 【解答】解： （x2） （2x+1）0， x20 或 2x+10， 所以 x12，x2 18 （5 分）如图，AB 是O 的直径，弦 CDAB 于点 H，A30，CD4，求O 的半径的长 【分析】连接 BC，由圆周角定理和垂径定理得出ACB90，CHDHCD2，由直角三角形 的性质得出 AC2CH4，ACBC4，AB2BC，得出 BC4，AB8，求出 OA4 即可 【解答】解：连接 BC，如图所示： AB 是O 的直径，弦 CDAB 于 H， ACB90，CHDHCD2，AHC90， A30， AC2CH4， 在 RtABC 中，A30， ACBC4，AB2BC， B
26、C4，AB8， OA4， 即O 的半径长是 4 19 （5 分）如图，正方形 ABCD 的边长为 4，E 是 CD 中点，点 P 在射线 AB 上，过点 P 作线段 AE 的垂线 段，垂足为 F （1）求证：PAFAED； （2）连接 PE，若存在点 P 使PEF 与AED 相似，直接写出 PA 的长 2 或 5 【分析】 （1）根据两角对应相等两三角形相似证明即可 （2）分两种情形：当 PAPB2 时，易知 PEAD，此时DAEPEF，DPFE90，可得 PEFEAD当AEDPEF，DPFE 时，ADEPFE，分别求解即可 【解答】 （1）证明：在正方形 ABCD 中，D90，CDAB， A
27、EDPAF， PFAE， DPFA90， PAFAED （2）解：当 PAPB2 时，DEEC，APPB， PEAD，此时DAEPEF，DPFE90，可得PEFEAD 当AEDPEF，DPFE 时，ADEPFE， CDAB， AEDEAPAEP， PAPE， PFAE， AFFE， AD4，DEEC2，D90， AE2， AF， PAFAED， ， ， PA5， 综上所述，满足条件的 PA 的值为 2 或 5 20 （5 分）二次函数 yax2+bx+c（a，b，c 是常数，a0）的自变量 x 与函数值 y 的部分对应值如下表： x 3 2 1 0 1 y ax2+bx+c 4 4 m 根据以
28、上列表，回答下列问题： （1）直接写出 c，m 的值； （2）求此二次函数的解析式 【分析】 （1）根据表格中对应值可知对称轴的值和抛物线与 y 轴的交点，即可求得 c 的值，根据抛物线 的对称性即可求得 m 的值； （2）直接利用待定系数法求出二次函数解析式即可 【解答】解： （1）根据图表可知： 二次函数 yax2+bx+c 的图象过点（0，4） ， （2，4） ， 对称轴为直线 x1，c4， （3，）的对称点为（1，） ， m； （2）对称轴是直线 x1， 顶点为（1，） ， 设 ya（x+1）2+， 将（0，4）代入 ya（x+1）2+得， a+4， 解得 a， 这个二次函数的解析式为
29、 y（x+1）2+ 21 （5 分）关于 x 的一元二次方程（k2）x24x+20 有两个不相等的实数根 （1）求 k 的取值范围； （2）如果符合条件的最大整数 k 是一元二次方程 k2+mk+10 的根，求 m 的值 【分析】 （1）根据一元二次方程的定义和判别式的意义得到 k20 且（4） 24（k2） 20， 然后求出两不等式的公共部分即可； （2）满足条件的 k 的值为 3，然后把 k3 代入 k2+mk+10 得 9+3m+10，然后解关于 m 的方程即可 【解答】解： （1）根据题意得 k20 且（4）24（k2）20， 解得 k4 且 k2； （2）符合条件的最大整数 k3，
30、把 k3 代入 k2+mk+10 得 9+3m+10，解得 m 22 （5 分）如图，在平面直角坐标系 xOy 中，直线 yx+3 与函数 y（x0）的图象交于点 A（1，m） ， 与 x 轴交于点 B （1）求 m，k 的值； （2）过动点 P（0，n） （n0）作平行于 x 轴的直线，交函数 y（x0）的图象于点 C，交直线 y x+3 于点 D 当 n2 时，求线段 CD 的长； 若 CDOB，结合函数的图象，直接写出 n 的取值范围 【分析】 （1） 先利用一次函数解析式确定 m 的值得到 A 点坐标， 然后把 A 点坐标代入 y得到 k 的值； （2） 利用 C、 D 的纵坐标都为
31、2 得到 C 点和 D 点的横坐标， 然后求两横坐标之差得到线段 CD 的长； 先确定（3，0） ，由于 C、D 的纵坐标都为 n，根据一次函数和反比例函数图象上点的坐标特征可表 示出 C（，n） ，D（n3，n） ，讨论：当点 C 在点 D 的右侧时，先利用 CDOB 得到（n3）3， 解得 n12，n22（舍去） ，再结合图象可判断当 0n2 时，CDOB；当点 C 在点 D 的左侧时， 先利用 CDOB 得到 n33，解得 n13+，n23（舍去） ，再结合图象可判断当 n 3+时，CDOB 【解答】解： （1）直线 yx+3 经过点 A（1，m） ， m1+34， 反比例函数的图象经过
32、点 A（1，4） ， k144； （2）当 n2 时，点 P 的坐标为（0，2） ， 当 y2 时，2，解得 x2， 点 C 的坐标为（2，2） ， 当 y2 时，x+32，解得 x1， 点 D 的坐标为（1，2） ， CD2（1）3； 当 y0 时，x+30，解得 x3，则 B（3，0） 当 yn 时，n，解得 x， 点 C 的坐标为（，n） ， 当 yn 时，x+3n，解得 xn3， 点 D 的坐标为（n3，n） ， 当点 C 在点 D 的右侧时， 若 CDOB，即（n3）3，解得 n12，n22（舍去） ， 当 0n2 时，CDOB； 当点 C 在点 D 的左侧时， 若 CDOB，即 n
33、33，解得 n13+，n23（舍去） ， 当 n3+时，CDOB， 综上所述，n 的取值范围为 0n2 或 n3+ 23 （6 分）如图，在ABC 中，ABAC，以 AC 为直径的O 与 BC 交于点 D，DEAB，垂足为 E，ED 的延长线与 AC 的延长线交于点 F （1）求证：DE 是O 的切线； （2）若O 的半径为 2，BE1，求 CF 的长 【分析】 （1）如图，连结 OD，欲证 DE 是O 的切线，只需证得 ODED； （2）求出 AE，证AEDDEB，求出 DE，证FODFAE，求得 FD，由勾股定理求得 FO，根据 线段和差可求得 CF 【解答】 （1）证明：如图，连接 OD
34、，AD， AC 是直径， ADBC， 又在ABC 中，ABAC， BDCD， AOOC， ODAB， 又DEAB， DEOD， OD 为O 半径， DE 是O 的切线； （2）解：O 的半径为 2，ABAC， ACAB2+24， BE1， AE413， 过 O 作 OHAB 于 H， 则四边形 ODEH 是矩形， EHOD2， AH1， AHAO， AOH30， BAC60， AF2AE6， CFAFAC2 DEAB，ADBC， AEDBEDADB90， DAE+ADE90，ADE+BDE90， DAEBDE， AEDDEB， ， ， 解得：DE， ODAB， FODFAE， ， ， 解得：F
35、D2， 在 RtFOD 中，FO4， CFFOOC422 24 （6 分）某超市销售一款洗手液，这款洗手液成本价为每瓶 16 元，当销售单价定为每瓶 20 元时，每天 可售出 60 瓶市场调查反应：销售单价每上涨 1 元，则每天少售出 5 瓶若设这款洗手液的销售单价上 涨 x 元，每天的销售量利润为 y 元 （1）每天的销售量为 （605x） 瓶，每瓶洗手液的利润是 （4+x） 元； （用含 x 的代数式表示） （2）若这款洗手液的日销售利润 y 达到 300 元，则销售单价应上涨多少元？ （3）当销售单价上涨多少元时，这款洗手液每天的销售利润 y 最大，最大利润为多少元？ 【分析】 （1）根
36、据题意列代数式即可得到结论； （2）根据题意列方程，解方程即可得到结论； （3）根据题意列函数解析式，根据二次函数的性质即可得到结论 【解答】解： （1）每天的销售量为（605x）瓶，每瓶洗手液的利润是（4+x）元； 故答案为： （605x） ； （4+x） ； （2）根据题意得， （605x） （4+x）300， 解得：x16，x22， 答：销售单价应上涨 2 元或 6 元； （3）根据题意得，y（605x） （4+x）5（x12） （x+4）5（x4）2+320， 答：当销售单价上涨 4 元时，这款洗手液每天的销售利润 y 最大，最大利润为 320 元 25 （6 分）有这样一个问题：探究
37、函数 yx24|x|+3 的图象与性质 小丽根据学习函数的经验，对函数 yx24|x|+3 的图象与性质进行了探究 下面是小丽的探究过程，请补充完整： （1）函数 yx24|x|+3 的自变量 x 的取值范围是 任意实数 （2）如图，在平面直角坐标系 xOy 中，画出了函数 yx24|x|+3 的部分图象，用描点法将这个函数的 图象补充完整： （3）对于上面的函数 yx24|x|+3，下列四个结论： 函数图象关于 y 轴对称； 函数既有最大值，也有最小值； 当 x2 时，y 随 x 的增大而增大，当 x2 时，y 随 x 的增大而减小； 函数图象与 x 轴有 2 个公共点 所有正确结论的序号是
38、 （4）结合函数图象，解决问题： 若关于 x 的方程 x24|x|+3k 有 4 个不相等的实数根，则 k 的取值范围是 1k3 【分析】 （1）根据函数解析式可以写出 x 的取值范围； （2）根据函数图象的特点，可以得到该函数关于 y 轴对称，从而可以画出函数的完整图象； （3）根据函数图象可以判断各个小题中的结论是否成立； （4）根据函数图象，可以写出关于 x 的方程 x24|x|+3k 有 4 个不相等的实数根时，k 的取值范围 【解答】解： （1）函数 yx24|x|+3， x 的取值范围为任意实数， 故答案为：任意实数； （2）由函数 yx24|x|+3 可知，x0 和 x0 时的函
39、数图象关于 y 轴对称，函数图象如右图所示； （3）由图象可得， 函数图象关于 y 轴对称，故正确； 函数有最小值，但没有最大值，故错误； 当 x2 时，y 随 x 的增大而增大，当 x2 时，y 随 x 的增大而减小，故正确； 函数图象与 x 轴有 4 个公共点，故错误； 故答案为：； （4）由图象可得， 关于 x 的方程 x24|x|+3k 有 4 个不相等的实数根，则 k 的取值范围是1k3， 故答案为：1k3 26 （6 分）在平面直角坐标系 xOy 中，抛物线 ymx2+2mx3 与 x 轴交于 A，B 两点（点 A 在点 B 左侧） ， 与 y 轴交于点 C，AB4 （1）直接写出
40、抛物线的对称轴为直线 x1 ，点 A 的坐标为 （3，0） ； （2）求抛物线的解析式（化为一般式） ； （3）若将抛物线 ymx2+2mx3 沿 x 轴方向平移 n（n0）个单位长度，使得平移后的抛物线与线段 AC 恰有一个公共点，结合函数图象，回答下列问题： 若向左平移，则 n 的取值范围是 0n4 若向右平移，则 n 的取值范围是 0n2 【分析】 （1）由对称轴为直线 x，可求解； （2）将点 B 坐标代入可求解； （3）设向左平移后的解析式为：y（x+1+n）24，设向右平移后的解析式为：y（x+1n）24， 利用特殊点代入可求解 【解答】解： （1）抛物线 ymx2+2mx3 的对
41、称轴为直线 x1，AB4， 点 A（3，0） ，点 B（1，0） ， 故答案为：x1， （3，0） ； （2）抛物线 ymx2+2mx3 过点 B（1，0） ， 0m+2m3， m1， 抛物线的解析式：yx2+2x3， （3）如图， yx2+2x3（x+1）24， 设向左平移后的解析式为：y（x+1+n）24， 把 x3，y0 代入解析式可得：0（3+1+n）24， n0（舍去） ，n4， 向左平移，则 n 的取值范围是 0n4； 设向右平移后的解析式为：y（x+1n）24， 把 x0，y3 代入解析式可得：3（1n）24， n0（舍去） ，n2， 向右平移，则 n 的取值范围是 0n2， 故
42、答案为：0n4；0n2 27 （7 分）如图 1，ABC 和DEF 都是等腰直角三角形，A90，E90，DEF 的顶点 D 恰 好落在ABC 的斜边 BC 中点，把DEF 绕点 D 旋转，始终保持线段 DE、DF 分别与线段 AB、AC 交于 M、N，连接 MN 在这个变化过程中，小明通过观察、度量，发现了一些特殊的数量关系 （1）于是他把DEF 旋转到特殊位置，验证自己的猜想如图 2，当 MNBC 时， 通过计算BMD 和NMD 的度数，得出BMD NMD（填，或） ； 设 BC2，通过计算 AM，MN，NC 的长度，其中 NC ，进而得出 AM、MN、NC 之间的 数量关系是 AM+MNC
43、N （2）在特殊位置验证猜想还不够，还需要在一般位置进行证明 请你对（1）中猜想的线段 AM、MN、NC 之间的数量关系进行证明 【分析】 （1）由“SAS”可证BMDCND，可得BMDDNC，由外角的性质和平行线的性 质可证BMDCNDBDMCMN； 由等腰三角形的性质可求 BMBDNC，再求出 AM2，MNAM22，即可得 结论； （2）在 CN 上截取 CHAM，连接 AD，DH，由“SAS”可证AMDCHD，可得 MDDH，ADM CDH，再由“SAS”可证MDNHDN，可得 MNHN，可得结论 【解答】解： （1）ABC 和DEF 都是等腰直角三角形，A90，E90， BCEDF45
44、，ABAC，BCAB， MNBC， AMNB45ANMC，DMNBDM， AMAN， BMCN， 点 D 是 BC 中点， BDCD， 在BMD 和CND 中， ， BMDCND（SAS） ， BMDDNC， MDBC+DNCMDN+BDM， BDMCND， BMDCNDBDMCMN， 故答案为：； BC2，BCAB， ABAC2， BMDCNDBDM， BDBMBC， NC， AM2， AMAN，A90， MNAM22， AM+MN2+22NC， 故答案为：；AM+MNNC； （2）如图 1，在 CN 上截取 CHAM，连接 AD，DH， ABC 是等腰直角三角形，点 D 是 BC 中点，
45、ADCD，BADACD45，ADBC， 又AMCH， AMDCHD（SAS） ， MDDH，ADMCDH， ADM+ADNMDN45， ADN+CDH45， HDN45MDN， 在MDN 和HDN 中， ， MDNHDN（SAS） ， MNHN， NCCH+NHAM+MN 28 （7 分）在平面直角坐标系 xOy 中，O 的半径为 1，对于O 和O 外的点 P，给出如下的定义：若在 O 上存在一点 Q，使得 P、Q 两点间的距离小于或等于 1，则称 P 为O 的近距点 （1）在点 P1（1，1） ，P2（，） ，P3（0，） ，P4（2，1）中，O 的近距点是 P1 ； （2）若直线 l：yx
46、+b 上存在O 的近距点，求 b 的取值范围； （3）若点 P 在直线 yx+1 上，且点 P 是O 的近距点，求点 P 横坐标 xP的取值范围 【分析】 （1）按照新定义，利用构成三角形三边的关系，逐个验证即可求解； （2）如图 1，平移直线 l 至图示与半径为 2 的圆相切的位置，即 l 和 l的位置，当直线 l 位于图示 l 和 l之间的位置时，直线 l：yx+b 上存在O 的近距点，进而求解； （3）直线 yx+1 与半径为 1 的圆交于点 E、F，则点 P 点在 BE 和 CF 之间的位置时，符合题意，进而 求解 【解答】解： （1）由题意得：OQ1， P1（1，1） ，P2（，）
47、，P3（0，） ，P4（2，1）的坐标知，点 P2、P3都不在圆 O 外，故不符 合题意； 对于 P1，OP1，则 OP1OQP1QOP1+OQ，即1P1Q+1， 故存在 P1Q1，故点 P1符合题意； 同理可得 OP4，则1P4Q+1， 故不存在 P4Q1，故点 P4符合题意； 故答案为 P1； （2）如图 1，平移直线 l 至图示与半径为 2 的圆相切的位置，即 l 和 l的位置， 当直线 l 位于图示 l 和 l之间的位置时，直线 l：yx+b 上存在O 的近距点， 设直线 l 与圆切于点 A，则OAB 为等腰直角三角形，则 OBOA2b， 同理当直线 l 处于 l的位置时，b2， 故 b 的取值范围为2b2； （3）如图 2，作半径为 2 的同心圆 O，与直线 yx+1 交于点 B、C， 设直线 yx+1 与半径为 1 的圆交于点 E、F，则点 P 点在 BE 和 CF 之间的位置时，符合题意， 设点 B 的坐标为（x，x+1） ， 过点 B 作 BHy 轴于点 H，连接 OB、OC， 在 RtOBH 中，OB2
