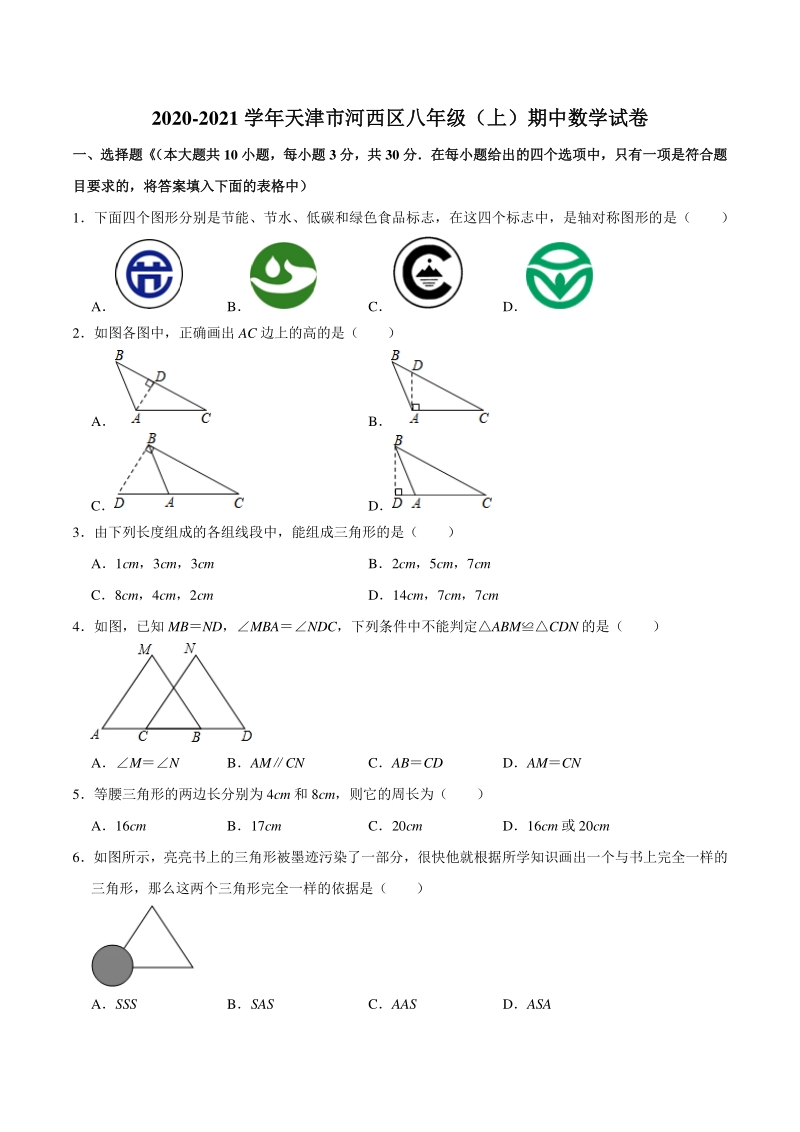
1、2020-2021 学年天津市河西区八年级（上）期中数学试卷学年天津市河西区八年级（上）期中数学试卷 一、选择题 （本大题共一、选择题 （本大题共 10 小题，每小题小题，每小题 3 分，共分，共 30 分在每小题给出的四个选项中，只有一项是符合题分在每小题给出的四个选项中，只有一项是符合题 目要求的，将答案填入下面的表格中）目要求的，将答案填入下面的表格中） 1下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（ ） A B C D 2如图各图中，正确画出 AC 边上的高的是（ ） A B C D 3由下列长度组成的各组线段中，能组成三角形的是（ ） A1cm
2、，3cm，3cm B2cm，5cm，7cm C8cm，4cm，2cm D14cm，7cm，7cm 4如图，已知 MBND，MBANDC，下列条件中不能判定ABMCDN 的是（ ） AMN BAMCN CABCD DAMCN 5等腰三角形的两边长分别为 4cm 和 8cm，则它的周长为（ ） A16cm B17cm C20cm D16cm 或 20cm 6如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的 三角形，那么这两个三角形完全一样的依据是（ ） ASSS BSAS CAAS DASA 7下列说法中，错误的是（ ） A三角形中至少有一个内角不小于 6
3、0 B三角形的角平分线、中线、高均在三角形的内部 C三角形两边之差小于第三边 D多边形的外角和等于 360 8如果 n 边形的内角和是它外角和的 3 倍，则 n 等于（ ） A6 B7 C8 D9 9如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相 等，凉亭的位置应选在（ ） AABC 的三条中线的交点 BABC 三条角平分线的交点 CABC 三条高所在直线的交点 DABC 三边的中垂线的交点 10点（1，2m1）关于直线 xm 的对称点的坐标是（ ） A （2m1，1） B （1，2m1） C （1，12m） D （2m1，2m1） 二、填空题（本大
4、题共二、填空题（本大题共 6 小题，每小题小题，每小题 3 分，共分，共 18 分）分） 11木工师傅在做完门框后为防止变形，常如图所示那样钉上两条斜拉的木板条，这样做的数学依据 是 12如图，ABAC，要使ABEACD，依据 ASA，应添加的一个条件是 13ABC 中，A：B：C1：3：5，则C 14在ABC 中，AC 的垂直平分线交 AC 于 E，交 BC 于 D，ABC 的周长是 17cm，AC5cm，ABD 的 周长是 cm 15如图，在等边ABC 中，BDCE，AD 与 BE 相交于点 F，则AFE 16如图，在ABC 中，A64，ABC 与ACD 的平分线交于点 A1，则A1 ；A
5、1BC 与 A1CD 的平分线相交于点 A2，得A2；An1BC 与An1CD 的平分线相交于点 An，要使An的 度数为整数，则 n 的值最大为 三、解答题（本大题共三、解答题（本大题共 7 小题，共小题，共 52 分，解答应写出文字说明、演算步骤或推理过程）分，解答应写出文字说明、演算步骤或推理过程） 17 （6 分）已知：CAB 求作：CAB 的角平分线 AD （尺规作图，保留作图痕迹，不写作法） 18 （6 分）已知：如图，已知ABC 中，其中 A（0，2） ，B（2，4） ，C（4，1） （1）画出与ABC 关于 y 轴对称的图形A1B1C1； （2）写出A1B1C1各顶点坐标； （
6、3）求ABC 的面积 19 （6 分）如图所示，BADCAD，ABAC求证：BDCD 20 （8 分）已知 AE、AD 分别是ABC 的高和角平分线，且B46，C60，求DAE 的度数 21 （8 分）如图，已知平面直角坐标系中，AOB 是等腰直角三角形，点 A 坐标为（2，3） ，求点 B 的坐 标 22 （8 分）如图，点 C 在线段 AB 上，ADEB，ACBE，ADBC，CF 平分DCE试探索 CF 与 DE 的位置关系，并说明理由 23 （10 分）如图 1，ABC 的边 BC 在直线 l 上，ACBC，且 ACBC，EFP 的边 FP 也在直线 l 上， 边 EF 与边 AC 重合
7、，且 EFFP （1）在图 1 中，请你写出 AB 与 AP 所满足的数量关系和位置关系并说明理由； （2）将EFP 沿直线 l 向左平移到图 2 的位置时，EP 交 AC 于点 Q，连接 AP，BQ猜想并写出 BQ 与 AP 所满足的数量关系和位置关系，并证明你的猜想； （3） 将EFP 沿直线 l 向左平移到图 3 的位置时， EP 的延长线交 AC 的延长线于点 Q， 连接 AP， BQ 你 认为（2）中所猜想的 BQ 与 AP 的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说 明理由 2020-2021 学年天津市河西区八年级（上）期中数学试卷学年天津市河西区八年级（上）
8、期中数学试卷 参考答案与试题解析参考答案与试题解析 一、选择题 （本大题共一、选择题 （本大题共 10 小题，每小题小题，每小题 3 分，共分，共 30 分在每小题给出的四个选项中，只有一项是符合题分在每小题给出的四个选项中，只有一项是符合题 目要求的，将答案填入下面的表格中）目要求的，将答案填入下面的表格中） 1下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（ ） A B C D 【分析】结合轴对称图形的概念进行求解即可 【解答】解：A、不是轴对称图形，本选项不符合题意； B、是轴对称图形，本选项符合题意； C、不是轴对称图形，本选项不符合题意； D、不是
9、轴对称图形，本选项不符合题意 故选：B 2如图各图中，正确画出 AC 边上的高的是（ ） A B C D 【分析】根据三角形高的定义，过点 B 与 AC 边垂直，且垂足在边 AC 上，然后结合各选项图形解答 【解答】解：根据三角形高线的定义，只有 D 选项中的 BE 是边 AC 上的高 故选：D 3由下列长度组成的各组线段中，能组成三角形的是（ ） A1cm，3cm，3cm B2cm，5cm，7cm C8cm，4cm，2cm D14cm，7cm，7cm 【分析】利用三角形的三边关系进行判断即可 【解答】解：A、1+33，能组成三角形，故此选项符合题意； B、2+57，不能组成三角形，故此选项不
10、符合题意； C、2+48，不能组成三角形，故此选项不符合题意； D、7+714，不能组成三角形，故此选项不符合题意； 故选：A 4如图，已知 MBND，MBANDC，下列条件中不能判定ABMCDN 的是（ ） AMN BAMCN CABCD DAMCN 【分析】根据三角形全等的判定定理，有 AAS、SSS、ASA、SAS 四种逐条验证即可 【解答】解：A、MN，符合 ASA，能判定ABMCDN，故 A 选项不符合题意； B、AMCN，得出MABNCD，符合 AAS，能判定ABMCDN，故 D 选项不符合题意 C、ABCD，符合 SAS，能判定ABMCDN，故 B 选项不符合题意； D、根据条件
11、 AMCN，MBND，MBANDC，不能判定ABMCDN，故 C 选项符合题意； 故选：D 5等腰三角形的两边长分别为 4cm 和 8cm，则它的周长为（ ） A16cm B17cm C20cm D16cm 或 20cm 【分析】根据等腰三角形的性质，本题要分情况讨论当腰长为 4cm 或是腰长为 8cm 两种情况 【解答】解：等腰三角形的两边长分别为 4cm 和 8cm， 当腰长是 4cm 时，则三角形的三边是 4cm，4cm，8cm，4cm+4cm8cm 不满足三角形的三边关系； 当腰长是 8cm 时，三角形的三边是 8cm，8cm，4cm，三角形的周长是 20cm 故选：C 6如图所示，亮
12、亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的 三角形，那么这两个三角形完全一样的依据是（ ） ASSS BSAS CAAS DASA 【分析】根据图象，三角形有两角和它们的夹边是完整的，所以可以根据“角边角”画出 【解答】解：根据题意，三角形的两角和它们的夹边是完整的，所以可以利用“角边角”定理作出完全 一样的三角形 故选：D 7下列说法中，错误的是（ ） A三角形中至少有一个内角不小于 60 B三角形的角平分线、中线、高均在三角形的内部 C三角形两边之差小于第三边 D多边形的外角和等于 360 【分析】 根据三角形的内角和定理可判定 A 选项； 由三角形的角
13、平分线， 高线， 中的性质可判定 B 选项； 由三角形的三边关系可判定 C 选项，由多边形的外角和定理可判定 D 选项 【解答】解：三角形中至少有一个内角不小于 60，故 A 选项说法正确； 三角形的角平分线、中线、均在三角形的内部，锐角三角形的高再三角形的内部，钝角三角形的高在三 角形的外部，故 B 选项说法错误； 三角形的任意两边之差小于第三边，故 C 选项说法正确； 多边形的外角和等于 360，故 D 选项说法正确， 故选：B 8如果 n 边形的内角和是它外角和的 3 倍，则 n 等于（ ） A6 B7 C8 D9 【分析】根据多边形内角和公式 180（n2）和外角和为 360可得方程
14、180（n2）3603，再解 方程即可 【解答】解：由题意得：180（n2）3603， 解得：n8， 故选：C 9如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相 等，凉亭的位置应选在（ ） AABC 的三条中线的交点 BABC 三条角平分线的交点 CABC 三条高所在直线的交点 DABC 三边的中垂线的交点 【分析】由于凉亭到草坪三条边的距离相等，所以根据角平分线上的点到边的距离相等，可知是ABC 三条角平分线的交点由此即可确定凉亭位置 【解答】解：凉亭到草坪三条边的距离相等， 凉亭选择ABC 三条角平分线的交点 故选：B 10点（1，2m1）关于直
15、线 xm 的对称点的坐标是（ ） A （2m1，1） B （1，2m1） C （1，12m） D （2m1，2m1） 【分析】根据关于直线 xm 的对称点的横坐标的中点在直线上，纵坐标相等解答 【解答】解：点（1，2m1）关于直线 xm 的对称点的坐标为（2m1，2m1） ， 故选：D 二、填空题（本大题共二、填空题（本大题共 6 小题，每小题小题，每小题 3 分，共分，共 18 分）分） 11木工师傅在做完门框后为防止变形，常如图所示那样钉上两条斜拉的木板条，这样做的数学依据是 三 角形具有稳定性 【分析】根据三角形具有稳定性进行解答 【解答】解：木工师傅在做完门框后为防止变形，常如图所示那
16、样钉上两条斜拉的木板条，这样做的数 学依据是三角形具有稳定性， 故答案为：三角形具有稳定性 12如图，ABAC，要使ABEACD，依据 ASA，应添加的一个条件是 CB 【分析】添加CB，再加上公共角AA，已知条件 ABAC 可利用 ASA 判定ABEACD 【解答】解：添加CB， 在ACD 和ABE 中， ABEACD（ASA） 故答案为：CB 13ABC 中，A：B：C1：3：5，则C 100 【分析】设Cx，根据A：B：C1：3：5 可知B3x，C5x，由三角形内角和定理即可 求出 x 的值，进而得出C 的值 【解答】解：设Cx， A：B：C1：3：5， B3x，C5x， A+B+C18
17、0， x+3x+5x180，解得 x20， C5x520100 故答案为：100 14在ABC 中，AC 的垂直平分线交 AC 于 E，交 BC 于 D，ABC 的周长是 17cm，AC5cm，ABD 的 周长是 12 cm 【分析】由 DE 是 AC 的垂直平分线，根据线段垂直平分线的性质，可得 ADCD，继而可得ABD 的 周长AB+BC，又由ABC 的周长是 17cm 及 AC5cm，即可求得 AB+BC12cm，从而可得，ABD 的周长 【解答】解：DE 是 AC 的垂直平分线， ADCD， ABC 的周长是 17cm，AC5cm， AB+BC175112（cm） ， ABD 的周长为
18、：AB+BD+ADAB+BD+CDAB+BC12cm 故答案为：12 15如图，在等边ABC 中，BDCE，AD 与 BE 相交于点 F，则AFE 60 【分析】利用等边三角形的性质结合全等三角形的判定方法得出ABDBCE，进而求出ABF+ CBEAFE 即可得出答案 【解答】解：ABC 是等边三角形， ABDC，ABBC， 在ABD 和BCE 中， ， ABDBCE（SAS） ， BADCBE， ABF+BAFAFE， ABF+CBEAFE60 故答案为：60 16如图，在ABC 中，A64，ABC 与ACD 的平分线交于点 A1，则A1 32 ；A1BC 与A1CD 的平分线相交于点 A2
19、，得A2；An1BC 与An1CD 的平分线相交于点 An，要使An 的度数为整数，则 n 的值最大为 6 【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得ACDA+ABC，A1CD A1+A1BC，根据角平分线的定义可得A1BCABC，A1CDACD，然后整理得到A1 A，由A1CDA1+A1BC，ACDABC+A，而 A1B、A1C 分别平分ABC 和ACD，得到 ACD2A1CD，ABC2A1BC，于是有A2A1，同理可得A12A2，即A22A2，因 此找出规律 【解答】解：由三角形的外角性质得，ACDA+ABC，A1CDA1+A1BC， ABC 的平分线与ACD 的平分线交
20、于点 A1， A1BCABC，A1CDACD， A1+A1BC（A+ABC）A+A1BC， A1A6432； A1B、A1C 分别平分ABC 和ACD， ACD2A1CD，ABC2A1BC， 而A1CDA1+A1BC，ACDABC+A， A2A1， A1A， 同理可得A12A2， A2A， A2nAn， An（）nA， An的度数为整数， n6 故答案为：32，6 三、解答题（本大题共三、解答题（本大题共 7 小题，共小题，共 52 分，解答应写出文字说明、演算步骤或推理过程）分，解答应写出文字说明、演算步骤或推理过程） 17 （6 分）已知：CAB 求作：CAB 的角平分线 AD （尺规作图
21、，保留作图痕迹，不写作法） 【分析】直接利用角平分线的坐标得出射线 AD 【解答】解：如图所示：AD 即为所求 18 （6 分）已知：如图，已知ABC 中，其中 A（0，2） ，B（2，4） ，C（4，1） （1）画出与ABC 关于 y 轴对称的图形A1B1C1； （2）写出A1B1C1各顶点坐标； （3）求ABC 的面积 【分析】 （1）根据轴对称变换的性质作图； （2）根据关于 y 轴对称的点的坐标特点解答； （3）根据矩形的面积公式和三角形的面积公式计算 【解答】解： （1）所作图形如图所示； （2）A1（0，2） ，B1（2，4） ，C1（4，1） ； （3）SABC342341221
22、23225 19 （6 分）如图所示，BADCAD，ABAC求证：BDCD 【分析】证明ABDACD（SAS） ，即可得出结论 【解答】证明：在ABD 和ACD 中， ， ABDACD（SAS） ， BDCD 20 （8 分）已知 AE、AD 分别是ABC 的高和角平分线，且B46，C60，求DAE 的度数 【分析】 先根据三角形的内角和定理得到BAC 的度数， 再利用角平分线的性质可求出DACBAC， 而EAC90C，然后利用DAEDACEAC 进行计算即可 【解答】解：在ABC 中，B46，C60 BAC180BC180466074 AD 是的角平分线 AE 是ABC 的高 AEC90 在
23、AEC 中，EAC180AECC180906030 DAEDACEAC37307 21 （8 分）如图，已知平面直角坐标系中，AOB 是等腰直角三角形，点 A 坐标为（2，3） ，求点 B 的坐 标 【分析】过 A 作 ACy 轴于 C，过 B 作 BDy 轴于 D，证明ACOODB（AAS） ，得 ACOD2， OCBD3，即可得出答案 【解答】解：过 A 作 ACy 轴于 C，过 B 作 BDy 轴于 D，如图所示： 则ACOBDO90， CAO+AOC90， 点 A 坐标为（2，3） ， AC2，OC3， AOB 是等腰直角三角形， OAOB，AOB90， AOC+BOD90， CAOB
24、OD， 在ACO 和ODB 中， ， ACOODB（AAS） ， ACOD2，OCBD3， 点 B 的坐标为（3，2） 22 （8 分）如图，点 C 在线段 AB 上，ADEB，ACBE，ADBC，CF 平分DCE试探索 CF 与 DE 的位置关系，并说明理由 【分析】根据平行线性质得出AB，根据 SAS 证ACDBEC，推出 DCCE，根据等腰三角形 的三线合一定理推出即可 【解答】解：CFDE，CF 平分 DE，理由是： ADBE， AB， 在ACD 和BEC 中 ， ACDBEC（SAS） ， DCCE， CF 平分DCE， CFDE 23 （10 分）如图 1，ABC 的边 BC 在直
25、线 l 上，ACBC，且 ACBC，EFP 的边 FP 也在直线 l 上， 边 EF 与边 AC 重合，且 EFFP （1）在图 1 中，请你写出 AB 与 AP 所满足的数量关系和位置关系并说明理由； （2）将EFP 沿直线 l 向左平移到图 2 的位置时，EP 交 AC 于点 Q，连接 AP，BQ猜想并写出 BQ 与 AP 所满足的数量关系和位置关系，并证明你的猜想； （3） 将EFP 沿直线 l 向左平移到图 3 的位置时， EP 的延长线交 AC 的延长线于点 Q， 连接 AP， BQ 你 认为（2）中所猜想的 BQ 与 AP 的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，
26、请说 明理由 【分析】 （1）由题意可得ABC 与EFP 是全等的等腰直角三角形，可得BACCAP45，AB AP，可得 APAB，APAB； （2）求出 CQCP，根据 SAS 证BCQACP，推出 APBQ，CBQPAC，根据三角形内角和 定理求出CBQ+BQC90，推出PAC+AQG90，求出AGQ90即可； （3）证明相等时思路同（1） ，证明垂直时，延长 QB 交 AP 于点 N，则PBNCBQ，借助全等得到 的角相等，得出APC+PBN90，进一步可得出结论 【解答】解： （1）APAB，APAB， ACBC，且 ACBC，边 EF 与边 AC 重合，且 EFFP ABC 与EFP
27、 是全等的等腰直角三角形， BACCAP45，ABAP， BAP90， APAB，APAB； （2）BQ 与 AP 所满足的数量关系是 APBQ，位置关系是 APBQ，理由如下： 延长 BQ 交 AP 于 G， 由（1）知，EPF45，ACP90， PQC45QPC， CQCP， 在BCQ 和ACP 中， ， BCQACP（SAS） ， APBQ，CBQPAC， ACB90， CBQ+BQC90， CQBAQG， AQG+PAC90， AGQ1809090， APBQ； （3）成立，理由如下： 如图，EPF45， CPQ45， 又ACBC， CQPCPQ45， CQCP， 在 RtBCQ 和 RtACP 中， ， RtBCQRtACP（SAS） ， BQAP， 如图 3，延长 QB 交 AP 于点 N， 则PBNCBQ， RtBCQRtACP， BQCAPC， 在 RtBCQ 中，BQC+CBQ90， APC+PBN90， PNB90， QBAP
