 浙江省宁波市慈溪市2020-2021学年八年级上学期数学期中考试试卷(解析版)
浙江省宁波市慈溪市2020-2021学年八年级上学期数学期中考试试卷(解析版)
《浙江省宁波市慈溪市2020-2021学年八年级上学期数学期中考试试卷(解析版)》由会员分享,可在线阅读,更多相关《浙江省宁波市慈溪市2020-2021学年八年级上学期数学期中考试试卷(解析版)(16页珍藏版)》请在七七文库上搜索。
1、浙江省宁波市慈溪市浙江省宁波市慈溪市 2020-2021 学年八年级上学期数学期中考试试卷学年八年级上学期数学期中考试试卷 一、选择题(每题一、选择题(每题 3 分,共分,共 30 分)分) 1.下列图案是轴对称图形的有( ) A. 1 个 B. 2 个 C. 3 个 D. 4 个 2.要求画 ABC 的边 AB 上的高,下列画法中,正确的是( ) A. B. C. D. 3.在数学表达式: - 中,是一元一次不等式 的有 ( ) A. 1 个 B. 2 个 C. 3 个 D. 4 个 4.如图,已知 ABC 的六个元素,则下面甲、乙、丙三个三角形中和 ABC 全等的图形是( ) A. 甲和乙
2、 B. 乙和丙 C. 只有乙 D. 只有丙 5.已知 ABC 的三个边之比为 3:4:5,则这个三角形是( ) A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形 6.下列叙述错误的是( ) A. 所有的命题都有条件和结论 B. 所有的命题都是定理 C. 所有的定理都是命题 D. 所有的公理都是真命题 7.如图是一株美丽的勾股树, 其中所有的四边形都是正方形, 所有的三角形都是直角三角形 若正方形 A, B,C,D 的边长分别是 3,5,2,3,则最大正方形 E 的面积是( ) A. 13 B. 26 C. 47 D. 94 8.若关于 x 的方程 的解是正数,则 a 的取
3、值范围是( ) A. B. C. a 为任何实数 D. a 为大于 0 的数 9.如图, DAC和 EBC均是等边三角形, AE、 BD分别与CD、 CE交于点M、 N, 有如下结论: ACEDCB; CM=CN;AC=DN其中,正确结论的个数是( ) A. 3 个 B. 2 个 C. 1 个 D. 0 个 10.关于 x 的不等式组 有四个整数解,则 a 的取值范围是( ) A. B. C. D. 二、填空题(每题二、填空题(每题 4 分,共分,共 24 分)分) 11. ABC 中, C=90,若 BC=12,AB=13,则 AC=_ 12.某电器商场促销,海尔某型号冰箱的售价是 2500
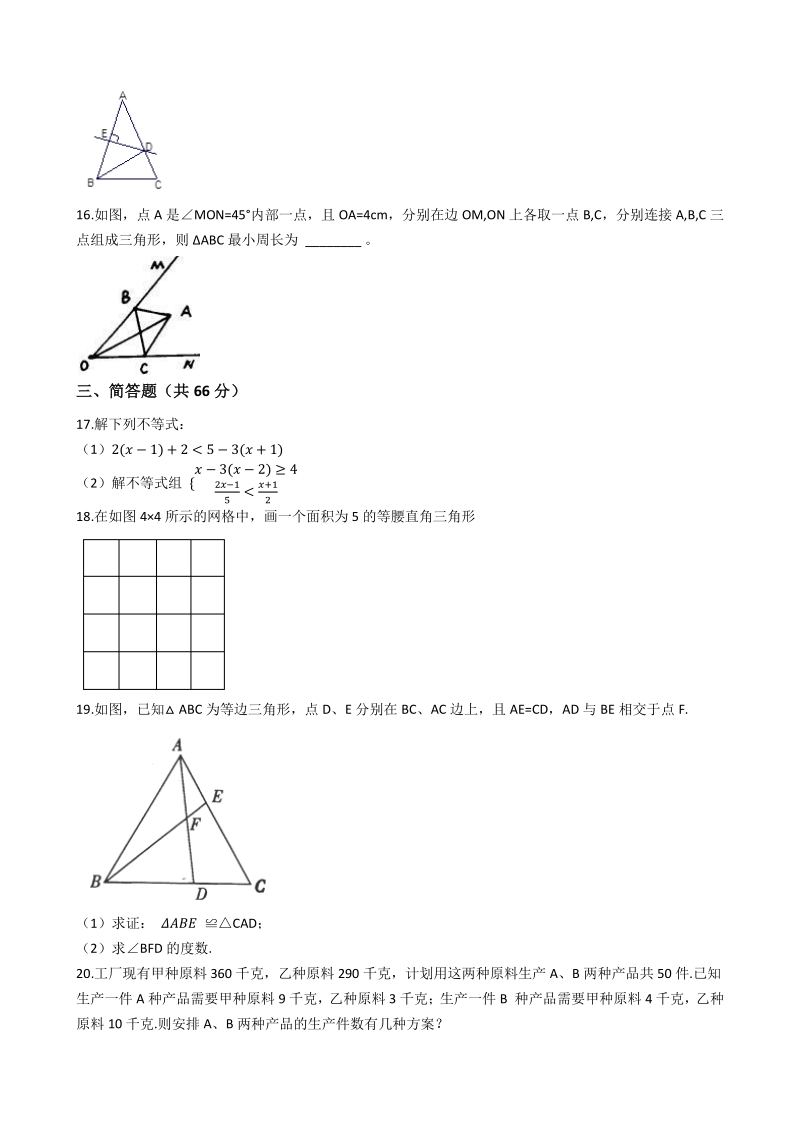
4、 元,进价是 1800 元,商场为保证利润率不低于 5%, 则海尔该型号冰箱最多降价_元. 13. ABC 中,如果两条直角边分别为 5,12,则斜边上的高线是_ 14.如图, ABC 的三边 AB, BC,CA 的长分别为 20,30,40, 其三条角平分线将 ABC 分为三个三角形, 则 SABO: SBCO:SAOC等于_。 15.如图,在 ABC 中,AB=AC,AB 的中垂线 DE 交 AC 于点 D,交 AB 于点 E,如果 BC=10, BDC 的周长 为 22,那么 AB=_ 16.如图,点 A 是MON=45内部一点,且 OA=4cm,分别在边 OM,ON 上各取一点 B,C
5、,分别连接 A,B,C 三 点组成三角形,则 ABC 最小周长为 _ 。 三、简答题(共三、简答题(共 66 分)分) 17.解下列不等式: (1) (2)解不等式组 18.在如图 44 所示的网格中,画一个面积为 5 的等腰直角三角形 19.如图,已知 ABC 为等边三角形,点 D、E 分别在 BC、AC 边上,且 AE=CD,AD 与 BE 相交于点 F. (1)求证: CAD; (2)求BFD 的度数. 20.工厂现有甲种原料 360 千克,乙种原料 290 千克,计划用这两种原料生产 A、B 两种产品共 50 件.已知 生产一件 A 种产品需要甲种原料 9 千克,乙种原料 3 千克;生
6、产一件 B 种产品需要甲种原料 4 千克,乙种 原料 10 千克.则安排 A、B 两种产品的生产件数有几种方案? 21.如图,在 Rt ABC 中,C=90,BC=6cm,AC=8cm,按图中所示方法将 BCD 沿 BD 折叠,使点 C 落在 AB 边的 C点,那么 ADC的面积是多少平方厘米? 22.老师请同学在一张长为 17cm,宽为 16cm 的长方形纸板上剪下一个腰长为 10cm 的等腰三角形(要求等 腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边上)请你帮同学们计算剪下的 等腰三角形的面积。 23.如图,在等腰 中,C=90,F 是 AB 边上的中点,点 D、E
7、分别在 AC、BC 边上运动,且保持 .连接 DE、DF、EF.在此运动变化的过程中,下列结论:求证 是等腰直角三角形; 24.定义:在三角形 ABC 中,若 BC=a,AC=b,AB=c,a,b,c 满足,ac+a2=b2则称这个三角形为“类勾股三角形”。 请根据以上定义解决下列问题: (1)命题:“直角三角形都是类勾股三角形”是_(填“真”或“假”)命题。 (2)如图(a)若等腰三角形 ABC“类勾股三角形”,其中 AB=BC,ACAB,请求A 的度数。 (3)如图(b),在三角形 ABC 中,B=2A,且CA 当A=32时,你能把这个三角形分成两个等腰三角形吗?若能请在(b)图中画出分割
8、线,并标注被分 割后的两个等腰三角形的顶角度数;若不能,请说明理由。 请证明三角形 ABC 为“勾股类三角形” 答案解析答案解析 一、选择题(每题 3 分,共 30 分) 1.【答案】 B 【考点】轴对称图形 【解析】【解答】解:第一、第四是轴对称图形,第二、第三是旋转对称图形。 故答案为:B 【分析】根据轴对称图形的概念,逐个判断即可。 2.【答案】 C 【考点】三角形的角平分线、中线和高 【解析】【解答】解:过点 C 作 AB 边的垂线,正确的是 C. 故答案为:C. 【分析】根据三角形的高的定义可知, ABC 的边 AB 上的高, 应从边 AB 所对的顶点 C 向 AB 或其延长 线作垂
9、线,顶点与垂足之间的线段长即为边 AB 上的高. 3.【答案】 A 【考点】一元一次不等式的定义 【解析】【解答】解:-30 是不等式,不是一元一次不等式; 4x+3y0 是二元一次不等式,不是一元一次不等式; x=3 是方程,不是一元一次不等式; x2+2xy+y2是三项式,不是一元一次不等式; x5 是一元一次不等式; x+2y+3 是二元一次不等式,不是一元一次不等式; 是一元一次不等式的有 1 个. 故答案为:A. 【分析】一元一次不等式:含有一个未知数,且未知数的次数是 1,未知数的系数不为 0,左右两边为整 式的不等式;依此逐一分析即可得出答案. 4.【答案】B 【考点】全等三角形
10、的判定 【解析】 【解答】解:图甲不符合三角形全等的判定定理,即图甲和 ABC 不全等; 图乙符合 SAS 定理, 即图乙和 ABC 全等; 图丙符合 AAS 定理,即图丙和 ABC 全等; 故选 B 【分析】全等三角形的判定定理有 SAS,ASA,AAS,SSS,根据定理逐个判断即可 5.【答案】 B 【考点】勾股定理的逆定理 【解析】【解答】解:依题可设三角形三边长分别是 3a,4a,5a, (3a)2+(4a)2=(5a)2 , 这个三角形是直角三角形, 故答案为:B. 【分析】根据题意可设三角形三边长分别是 3a,4a,5a,根据勾股定理逆定理即可得出答案. 6.【答案】 B 【考点】
11、定义、命题及定理的概念 【解析】【解答】解:A、 所有的命题都有条件和结论是正确的,A 不符合题意; B、所有的命题不一定是定理,是错误的,B 符合题意; C、 所有的定理都是命题,是正确的, C 不符合题意; D、 所有的公理都是真命题,是正确的, D 不符合题意; 故答案为:B. 【分析】命题:我们把用语言、符号或式子表达的,可以判断真假的陈述句;再由命题与定理、公理的 关系逐一分析即可得出答案. 7.【答案】C 【考点】勾股定理 【解析】【解答】解:如图, 根据勾股定理的几何意义,可得 A、B 的面积和为 S1 , C、D 的面积和为 S2 , S1+S2=S3 , 于是 S3=S1+S


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 浙江省 宁波市 慈溪市 2020 2021 学年 年级 上学 数学 期中考试 试卷 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-164065.html