1、2021 中考数学一轮专题训练：正方形及四边形综合问题中考数学一轮专题训练：正方形及四边形综合问题 一、选择题（本大题共一、选择题（本大题共 10 道小题）道小题） 1. 下列说法错误的是 ( ) A.平行四边形的对边相等 B.对角线相等的四边形是矩形 C.对角线互相垂直的平行四边形是菱形 D.正方形既是轴对称图形又是中心对称图形 2. 下列说法，正确的个数有 ( ) 正方形既是菱形又是矩形;有两个角是直角的四边形是矩形;菱形的对角线相等;对角 线互相垂直平分且相等的四边形是正方形. A.1 个 B.2 个 C.3 个 D.4 个 3. 小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方
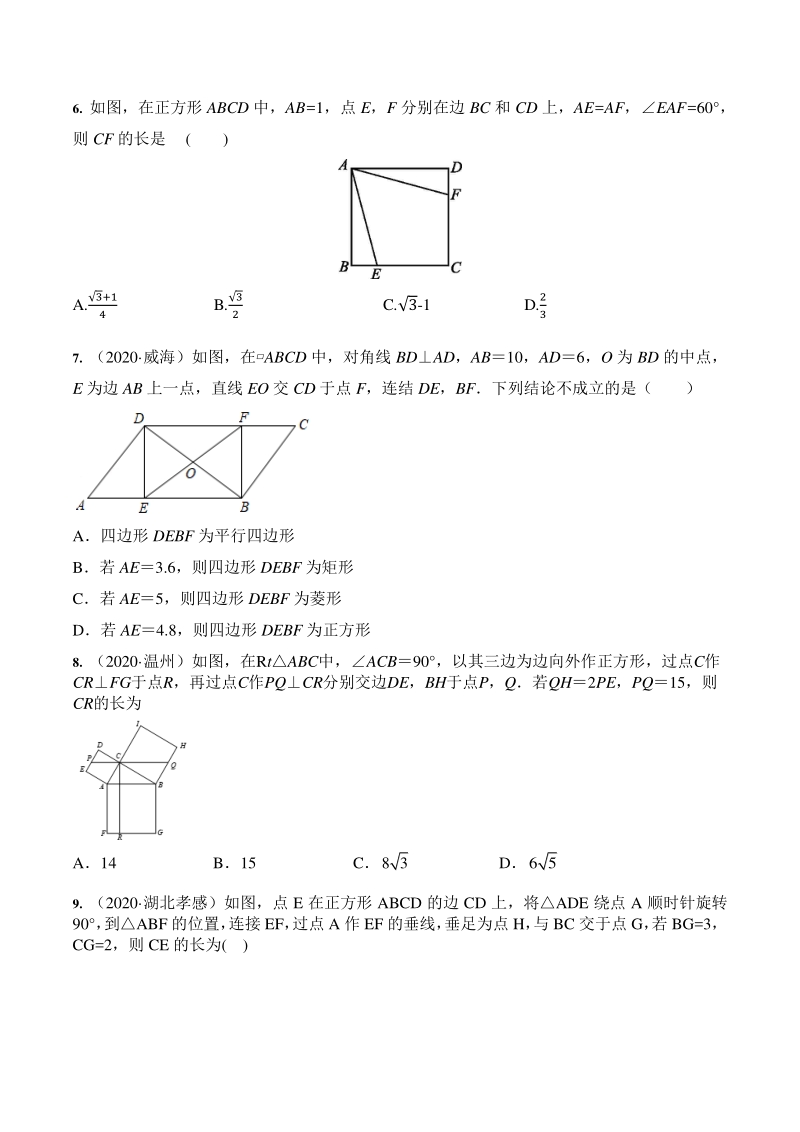
2、形，她对折了 ( ) A.1 次 B.2 次 C.3 次 D.4 次 4. 如图，四边形 ABCD 是边长为 5 的正方形，E 是 DC 上一点，DE=1，将 ADE 绕着点 A 顺 时针旋转到与 ABF 重合，则 EF= ( ) A.41 B.42 C.52 D.213 5. 如图，正方形 ABCD 的边长为 9，将正方形折叠，使顶点 D 落在 BC 边上的点 E 处，折痕 为 GH，若 BEEC21，则线段 CH 的长是( ) A. 3 B. 4 C. 5 D. 6 6. 如图，在正方形 ABCD 中，AB=1，点 E，F 分别在边 BC 和 CD 上，AE=AF，EAF=60 ， 则 C
3、F 的长是 ( ) A.3+1 4 B. 3 2 C.3-1 D.2 3 7. （2020 威海）如图，在ABCD 中，对角线 BDAD，AB10，AD6，O 为 BD 的中点， E 为边 AB 上一点，直线 EO 交 CD 于点 F，连结 DE，BF下列结论不成立的是（ ） A四边形 DEBF 为平行四边形 B若 AE3.6，则四边形 DEBF 为矩形 C若 AE5，则四边形 DEBF 为菱形 D若 AE4.8，则四边形 DEBF 为正方形 8. （2020 温州）如图，在RtABC中，ACB90 ，以其三边为边向外作正方形，过点C作 CRFG于点R，再过点C作PQCR分别交边DE，BH于点
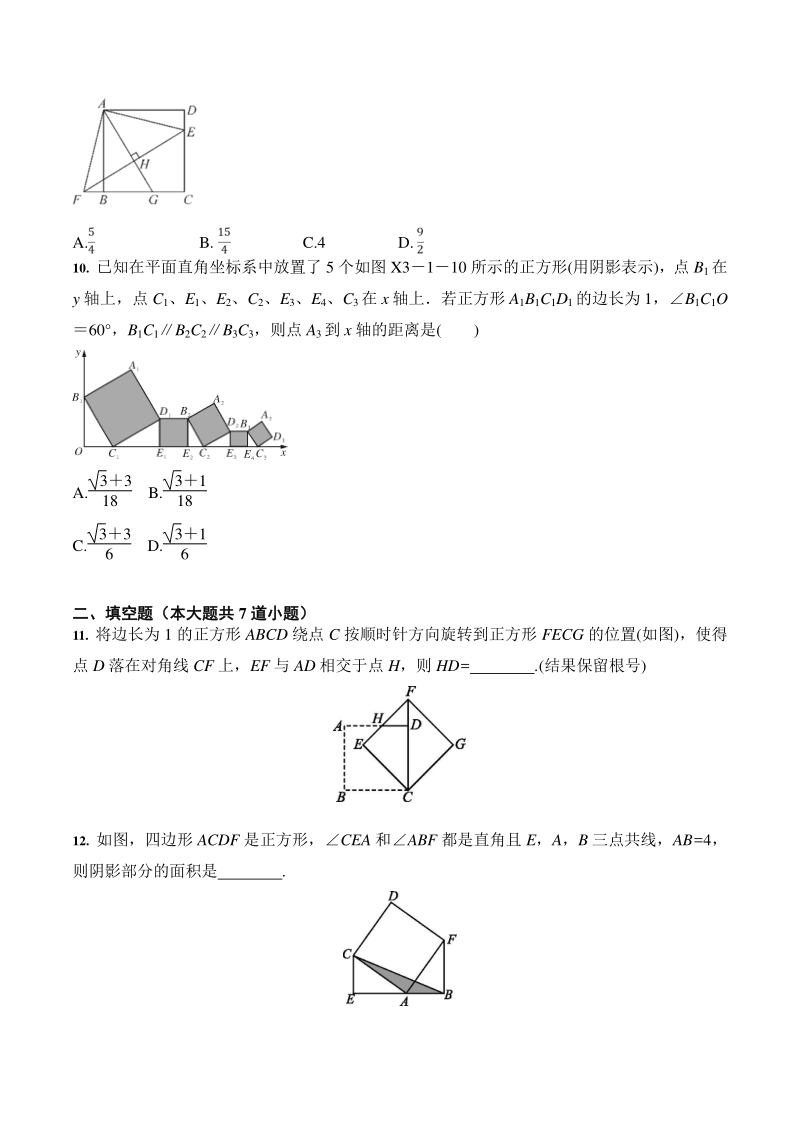
4、P，Q若QH2PE，PQ15，则 CR的长为 A14 B15 C8 3 D6 5 9. （2020 湖北孝感）如图，点 E 在正方形 ABCD 的边 CD 上，将ADE 绕点 A 顺时针旋转 90 ， 到ABF 的位置， 连接 EF， 过点 A 作 EF 的垂线， 垂足为点 H， 与 BC 交于点 G， 若 BG=3， CG=2，则 CE 的长为( ) A. B. C.4 D. 10. 已知在平面直角坐标系中放置了 5 个如图 X3110 所示的正方形(用阴影表示)，点 B1在 y 轴上，点 C1、E1、E2、C2、E3、E4、C3在 x 轴上若正方形 A1B1C1D1的边长为 1，B1C1O
5、 60 ，B1C1B2C2B3C3，则点 A3到 x 轴的距离是( ) A. 33 18 B. 31 18 C. 33 6 D. 31 6 二、填空题（本大题共二、填空题（本大题共 7 道小题）道小题） 11. 将边长为 1 的正方形 ABCD 绕点 C 按顺时针方向旋转到正方形 FECG 的位置(如图)，使得 点 D 落在对角线 CF 上，EF 与 AD 相交于点 H，则 HD= .(结果保留根号) 12. 如图，四边形 ACDF 是正方形，CEA 和ABF 都是直角且 E，A，B 三点共线，AB=4， 则阴影部分的面积是 . 13. 以正方形 ABCD 的边 AD 为边作等边三角形 ADE
6、，则BEC 的度数是 . 14. 如图，在正方形 ABCD 中，AC 为对角线，点 E 在 AB 边上，EFAC 于点 F，连接 EC， AF=3，若 EFC 的周长为 12，则 EC 的长为 . 15. 如图，正方形 ABCD 的边长为 2 2，对角线 AC，BD 相交于点 O，E 是 OC 的中点，连接 BE，过点 A 作 AMBE 于点 M，交 BD 于点 F，则 FM 的长为_ 16. 七巧板是一种古老的中国传统智力游戏，被誉为“东方魔板”.由边长为 42的正方形 ABCD 可以制作一副如图所示的七巧板，现将这副七巧板在正方形 EFGH 内拼成如图所示的“拼 搏兔”造型(其中点 Q，R
7、 分别与图中的点 E，G 重合，点 P 在边 EH 上)，则“拼搏兔”所在正 方形 EFGH 的边长是 . 17. 如图，正方形 ABCD 的面积为 3 cm2，E 为 BC 边上一点，BAE30 ，F 为 AE 的中点， 过点 F 作直线分别与 AB，DC 相交于点 M，N.若 MNAE，则 AM 的长等于_cm. 三、解答题（本大题共三、解答题（本大题共 4 道小题）道小题） 18. 如图， 在正方形 ABCD 中， 点 E 是 BC 的中点， 连接 DE， 过点 A 作 AGED 交 DE 于点 F， 交 CD 于点 G. (1)求证: ADGDCE; (2)连接 BF，求证:AB=FB
8、. 19. 如图，已知正方形 ABCD 与正方形 CEFG，M 是 AF 的中点，连接 DM，EM. (1)如图，点 E 在 CD 上，点 G 在 BC 的延长线上，判断 DM，EM 的数量关系与位置关系， 请直接写出结论. (2)如图，点 E 在 DC 的延长线上，点 G 在 BC 上，(1)中结论是否仍然成立?请证明你的结论. 20. 如图，在直角梯形 ABCD 中，AD90 ，AB8 cm，CD10 cm，AD6 cm，点 E 从点 A 出发，沿 ADC 方向运动，运动速度为 2 cm/s，点 F 同时从点 A 出发，沿 AB 方 向运动，运动速度为 1 cm/s.设运动时间为 t(s)
9、， CEF 的面积为 S(cm2) (1)当 0t3 时，t_，EF 10. (2)当 0t3 时(如图)，求 S 与 t 的函数关系式，并化为 Sa(th)2k 的形式，指出当 t 为何 值时，S 有最大值，最大值为多少？ (3)当 3t8 时(如图)，求 S 与 t 的函数关系式，并求出当 t 为何值时，S 有最大值，最大值为 多少？ 21. （2020 河南）将正方形ABCD的边AB绕点A逆时针旋转至AB，记旋转角为a.连接BB，过 点D作DE垂直于直线BB，垂足为点E，连接DB，CE. (1)如图1，当a=60 时，DEB的形状为 ，连接BD，可求出 BB CE 的值为 ； (2)当0
10、 a360 且a90时，(1)中的两个结论是否仍然成立?如果成立，请仅就图2的情形 进行证明；如果不成立，请说明理由； 当以点B、E、C、D为顶点的四边形是平行四边形时，请直接写出 BE B E 的值. 答案答案 一、选择题（本大题共一、选择题（本大题共 10 道小题）道小题） 1. 【答案】【答案】B 2. 【答案】【答案】B 3. 【答案】【答案】B 4. 【答案】【答案】D 解析由旋转的性质可知， ADEABF， BF=DE=1，FC=6，CE=4，EF=2+ 2=52=213.故选:D. 5. 【答案】【答案】B 【解析】设 CHx，BEEC21，BC9，EC3，由折叠可知，EH DH
11、9x，在 RtECH 中，由勾股定理得：(9x)232x2，解得：x4. 6. 【答案】【答案】C 解析连接 EF.AE=AF，EAF=60 ， AEF 为等边三角形，AE=EF.四 边形 ABCD 为正方形， B=D=C=90 ， AB=AD， Rt ABERt ADF(HL)， BE=DF， EC=CF.设 CF=x， 则 EC=x， AE=EF=2+ 2=2x， BE=1-x.在 Rt ABE 中， AB2+BE2=AE2， 1+(1-x)2=(2x)2，解得 x=3-1(舍负).故选 C. 7. 【答案】【答案】：O 为 BD 的中点， OBOD， 四边形 ABCD 为平行四边形， D
12、CAB， CDOEBO，DFOOEB， FDOEBO（AAS） ， OEOF， 四边形 DEBF 为平行四边形， 故 A 选顶结论正确， 若 AE3.6，AD6， ， 又， ， DAEBAD， DAEBAD， AEDADB90 故 B 选项结论正确， AB10，AE5， BE5， 又ADB90 ， DEAB5， DEBE， 四边形 DEBF 为菱形 故 C 选项结论正确， AE3.6 时，四边形 DEBF 为矩形，AE5 时，四边形 DEBF 为菱形， AE4.8 时，四边形 DEBF 不可能是正方形 故 D 不正确 故选：D 8. 【答案】【答案】A 【解析】 本题主要考查了相似三角形和正方
13、形的性质， 由题意知CDPCBQ， 所以 CDDP CBBQ ， 即 2 CDCDPE CBCBPE ，解得：BC2CD，所以 CQ2CP，则 CP5，CQ10，由于 PQAB，所 以CBABCQDCP，则 tanBCQtanDCPtanCBA 1 2 ，不妨设 DPx，则 DC2x， 在 RtDCP 中， 22 (2 )25xx， 解得 x 5.DC25， BC45， 所以 AB10， ABC 的斜边上的高 2 54 5 4 10 AC BC AB ,所以 CR14，所以因此本题选 A 9. 【答案】【答案】B 【解析】由旋转的性质得ABFADE，BF=DE，AF=AE，又AHEF，FH=E
14、H， 四边形 ABCD 是正方形，C=90 ，EFC=EFC，FHGFCE， FGFH FEFC ， BG=3，CG=2，BC=5，设 EC=x，则 BF=DE=5-x，FG=BG+BF=3+5-x=8-x， CF=BC+BF=5+5-x=10-x，EF= 22 ECCF=，FH= 22 (10) 2 xx , 22 22 (10) 8 2 10 (10) xx x x xx ，解得：x= 15 4 .故选 B. 10. 【答案】【答案】 7 2，0 D 解析：过小正方形的一个顶点 D3 作 FQx 轴于点 Q，过点 A3作 A3F FQ 于点 F. 正方形 A1B1C1D1的边长为 1，B1
15、C1O60 ，B1C1B2C2B3C3， B3C3E460 ，D1C1E130 ，E2B2C230 ， D1E11 2D1C1 1 2，D1E1B2E2 1 2 ， cos30 B2E2 B2C2 1 2 B2C2，解得：B2C2 3 3 . B3E4 3 6 ，cos30 B3E4 B3C3. 解得：B3C31 3. 则 D3C31 3. 根据题意得出： D3C3Q30 ，C3D3Q60 ，A3D3F30 ， D3Q1 2 1 3 1 6， FD3D3A3 cos30 1 3 3 2 3 6 . 则点 A3到 x 轴的距离 FQD3QFD31 6 3 6 31 6 . 二、填空题（本大题共二
16、、填空题（本大题共 7 道小题）道小题） 11. 【答案】【答案】2-1 解析四边形 ABCD 为正方形， CD=1，CDA=90 ， 边长为 1 的正方形 ABCD 绕点 C 按顺时针方向旋转到正方形 FECG 的位置，使得点 D 落在 对角线 CF 上， CF=2，CFE=45 ， DFH 为等腰直角三角形，DH=DF=CF-CD=2-1. 故答案为2-1. 12. 【答案】【答案】8 解析四边形 ACDF 是正方形， AC=AF，CAF=90 ，CAE+BAF=90 ， 又CAE+ECA=90 ， ECA=BAF，则在 ACE 和 FAB 中， = = 90， = ， = ， ACEFA
17、B(AAS)，AB=CE=4， 阴影部分的面积=1 2AB CE= 1 2 4 4=8. 13. 【答案】【答案】30 或 150 解析如图， ADE 是等边三角形， DE=DA，DEA=1=60 . 四边形 ABCD 是正方形， DC=DA，2=90 . CDE=150 ，DE=DC， 3=1 2(180 -150 )=15 . 同理可求得4=15 . BEC=30 . 如图， ADE 是等边三角形， DE=DA，1=2=60 ， 四边形 ABCD 是正方形， DC=DA，CDA=90 . DE=DC，3=30 ， 4=1 2(180 -30 )=75 . 同理可求得5=75 . BEC=3
18、60245=150 . 故答案为 30 或 150 . 14. 【答案】【答案】5 解析四边形 ABCD 是正方形，AC 为对角线， FAE=45 ，又EFAC， AFE=90 ，AEF=45 ， EF=AF=3， EFC 的周长为 12， FC=12-3-EC=9-EC， 在 Rt EFC 中，EC2=EF2+FC2， EC2=9+(9-EC)2， 解得 EC=5. 15. 【答案】【答案】 5 5 【解析】四边形 ABCD 为正方形，AOBO，AOFBOE90 ， AMBE，AFOBFM，FAOEBO，在 AFO 和 BEO 中， AOFBOE AOBO FAOEBO ， AFOBEO(A
19、SA)，FOEO，正方形 ABCD 的边长为 2 2，E 是 OC 的中点，FO EO1BF，BO2，在 RtBOE 中，BE 1222 5，由FBMEBO，FMB EOB，可得 BFMBEO，FM EO BF BE，即 FM 1 1 5，FM 5 5 . 16. 【答案】【答案】45 解析如图，连接 EG，作 GMEN 交 EN 的延长线于 M. 在 Rt EMG 中，GM=4，EM=2+2+4+4=12， EG=2+ 2=122+ 42=410， EH= 2 =45. 17. 【答案】【答案】2 3 3 或 3 3 【解析】如解图，过 N 作 NGAB，交 AB 于点 G，四边形 ABCD
20、 为正方形，ABADNG 3 cm，在 RtABE 中，BAE30 ，AB 3 cm，BE1 cm， AE2 cm， F为AE的中点， AF1 2AE1 cm， 在RtABE和RtNGM中， ABNG AENM， RtABERtNGM(HL)，BEGM，BAEMNG30 ，AEBNMG60 ， AFM90 ，即 MNAE，在 RtAMF 中，FAM30 ，AF1 cm，AM AF cos30 1 3 2 2 3 3 cm，由对称性得到 AMBMABAM 32 3 3 3 3 cm，综上，AM 的长等于 2 3 3 或 3 3 cm. 解图 三、解答题（本大题共三、解答题（本大题共 4 道小题）
21、道小题） 18. 【答案】【答案】 证明:(1)四边形 ABCD 是正方形， ADG=C=90 ，AD=DC， 又AGDE，DAG+ADF=90 =CDE+ADF，DAG=CDE， ADGDCE(ASA). (2)如图，延长 DE 交 AB 的延长线于 H， E 是 BC 的中点，BE=CE. 又C=HBE=90 ，DEC=HEB， DCEHBE(ASA)，BH=DC=AB，即 B 是 AH 的中点. 又AFH=90 ， Rt AFH 中，BF=1 2AH=AB. 19. 【答案】【答案】 解:(1)结论:DMEM，DM=EM. 解析延长 EM 交 AD 于 H. 四边形 ABCD 是正方形，
22、四边形 EFGC 是正方形， ADE=DEF=90 ， AD=CD， ADEF， MAH=MFE， AM=MF，AMH=FME， AMHFME， MH=ME，AH=EF=EC，DH=DE， EDH=90 ， DMEM，DM=ME. (2)结论不变.DMEM，DM=EM. 证明:延长 EM 交 DA 的延长线于 H. 四边形 ABCD 是正方形，四边形 EFGC 是正方形， ADE=DEF=90 ， AD=CD， ADEF， MAH=MFE， AM=MF，AMH=FME， AMHFME， MH=ME，AH=EF=EC， DH=DE， EDH=90 ， DMEM，DM=ME. 20. 【答案】【答
23、案】 (1) 2； 【解法提示】根据题意知，AFt，AE2t，A90 ，AF2AE2EF2，即 t2 (2t)2( 10)2，解得：t 2(负值舍去) (2)当 0t3 时，如解图，过点 C 作 CPAB，交 AB 延长线于点 P， 解图 AD90 ， 四边形 APCD 是矩形， 则 CPAD6 cm， AB8 cm，AD6 cm， BF(8t)cm，DE(62t)cm， 则 SS梯形ABCDS AEFS CBFS CDE 1 2 (810) 6 1 2 t 2t 1 2 (8t) 6 1 2 (62t) 10 t213t (t13 2 )2169 4 ， 即 S(t13 2 )2169 4
24、， 当 t13 2 时，S 随 t 的增大而增大， 当 t3 时，S 取得最大值，最大值为 30； (3)当 3t8 时，如解图，过点 F 作 FQCD 于点 Q， 解图 由AD90 ，知四边形 ADQF 是矩形， FQAD6 cm， ADDE2t，AD6 cm，CD10 cm， CE(162t)cm， 则此时 S1 2 (162t) 6486t， 60， S 随 t 的增大而减小， 当 t3 时，S 取得最大值，最大值为 30cm2 21. 【答案】【答案】 解： (1)等腰直角三角形，2. (2)两个结论仍成立. 证明:连接BD.AB=AB，BAB=a，ABB=90- 2 a ， BAD=
25、a-90 ，AD=AB，ABD=135- 2 a ，EBD=ABD-ABB=45. DEBB，EDB=EBD=45，DEB是等腰直角三角形， DB DE = 2. 四边形ABCD为正方形， BD CD = 2，BDC=45 . DB DE = BD CD ， EDB=BDC， EDB+EDB=BDC+EDB， 即BDB=CDE.BDBEDC， 2 BBBD CECD = ； 3或1.思路提示：分两种情况. 情形一，如图，当点B在BE上时，由 BB CE = 2，设BB=2m，CE=2m. CEBD，CE=BD，BD= 2m，在等腰直角三角形DEB中，斜边BD=2m， BE=DE=m，于是得到
26、BE B E 2 =3 mm m + =. 情形二，如图，当点B在BE延长线上时，由 BB CE = 2，设BB=2m，CE=2m. CEBD，CE=BD，BD= 2m，在等腰直角三角形DEB中，斜边BD=2m，BE=DE= m。于是得到 BE B E =1 m m =. 综上所述， BE B E 的值是3或1. 【解析】（1）ABB是等边三角形，ABD是等腰三角形，且ABD=75， DBE=45，结合DEBE，可得DEB是等腰直角三角形.连接BD，BDC=45 ，易得 BDB=CDE,结合2 DE BD DC BD ,BDBEDC， 2 CE BB BC BD . （2） 结论成立， 证明方法与（1）一样；（3）分两种情况：当点B在BE上时和当点B在BE延长线上时.
