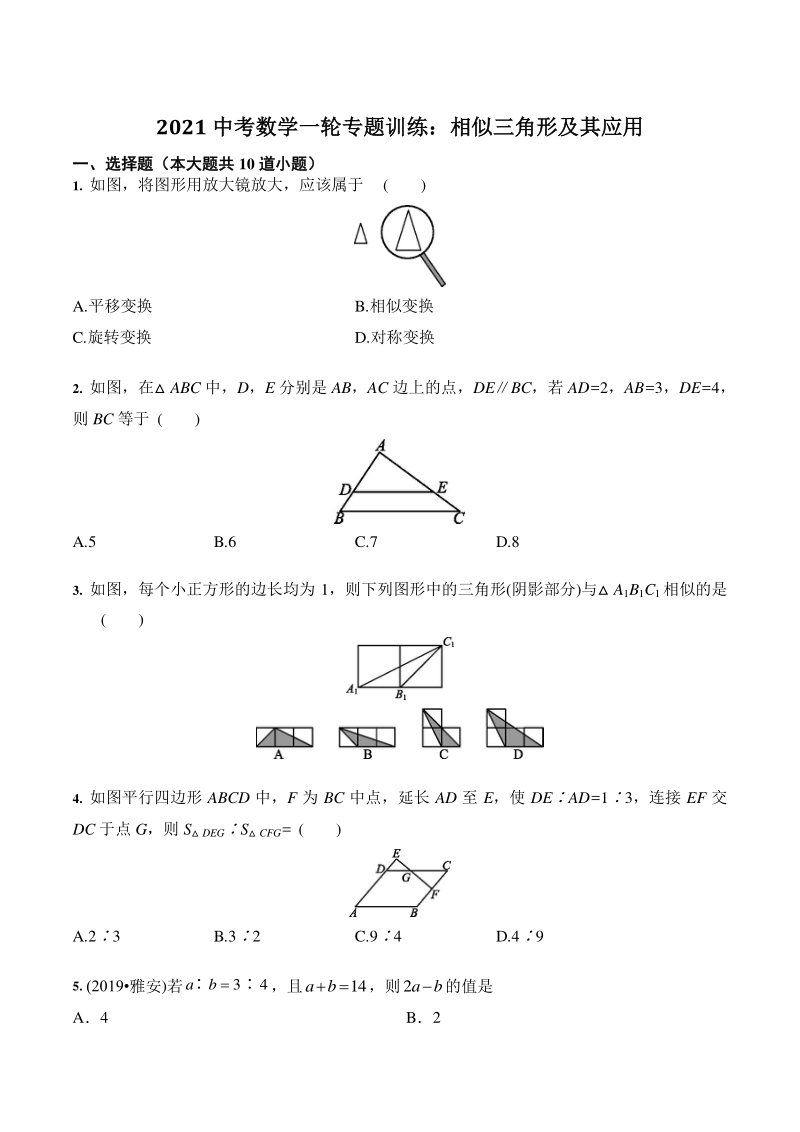
1、2021 中考数学一轮专题训练：相似三角形及其应用中考数学一轮专题训练：相似三角形及其应用 一、选择题（本大题共一、选择题（本大题共 10 道小题）道小题） 1. 如图，将图形用放大镜放大，应该属于 ( ) A.平移变换 B.相似变换 C.旋转变换 D.对称变换 2. 如图，在 ABC 中，D，E 分别是 AB，AC 边上的点，DEBC，若 AD=2，AB=3，DE=4， 则 BC 等于 ( ) A.5 B.6 C.7 D.8 3. 如图，每个小正方形的边长均为 1，则下列图形中的三角形(阴影部分)与 A1B1C1相似的是 ( ) 4. 如图平行四边形 ABCD 中，F 为 BC 中点，延长
2、AD 至 E，使 DEAD=13，连接 EF 交 DC 于点 G，则 S DEGS CFG= ( ) A.23 B.32 C.94 D.49 5. (2019雅安)若，且，则的值是 A4 B2 34ab 14a b 2a b C20 D14 6. 如图所示，P 是菱形 ABCD 的对角线 AC 上一动点，过 P 垂直于 AC 的直线交菱形 ABCD 的边于 M、N 两点，设 AC2，BD1，APx，AMN 的面积为 y，则 y 关于 x 的函数图 象的大致形状是( ) 7. 如图，长、宽均为 3，高为 8 的长方体容器，放置在水平桌面上，里面盛有水，水面高为 6，绕底面一棱进行旋转倾斜后，水面
3、恰好触到容器口边缘，图是此时的示意图，则图中 水面高度为 ( ) A.24 5 B.32 5 C.1234 17 D.2034 17 8. （2020 营口）如图，在 ABC 中，DEAB，且 CD BD = 3 2 ，则 CE CA 的值为（ ） A 3 5 B 2 3 C 4 5 D 3 2 9. （2020 重庆A卷） 如图， 在平面直角坐标系中， ABC的顶点坐标分别是A （1,2） ,B （1,1） ， C（3,1），以原点为位似中心，在原点的同侧画DEF，使DEF与ABC成位似图形，且相 似比为2:1，则线段DF的长度为（ ） A5 B2 C4 D2 5 A E CD B 10.
4、(2019贵港)如图，在中，点，分别在，边上， 若，则线段的长为 A B C D5 二、填空题（本大题共二、填空题（本大题共 7 道小题）道小题） 11. (2019郴州)若，则_ 12. （2020 吉林） 如图， 在ABC中，D，E分别是边AB，AC的中点 若ADE的面积为 1 2 则 四边形DBCE的面积为_ 13. （2020 郴州）郴州） 在平面直角坐标系中， 将AOB以点O为位似中心，3 2 为位似比作位似变换， 得到 11OB A.已知)3 , 2(A，则点 1 A的坐标是 ABCDEABACDEBCACDB 2ADBD6BC CD 2 33 2 2 6 3 2 xy x y x
5、 14. (2020绥化)在平面直角坐标系中，ABC 和A1B1C1的相似比等于 1 2 ，并且是关于原点 O 的位似图形，若点 A 的坐标为(2，4)，则其对应点 A1的坐标是_ 15. （2020深圳）如图，在四边形 ABCD 中，AC 与 BD 相交于点 O，ABCDAC90 ， tanACB1 2， BO OD 4 3，则 SABD SCBD_ 16. 如图，在 RtABC 中，ACB90 ，AC3， BC4， CDAB，垂足为 D， E 为 BC 的中点，AE 与 CD 交于点 F，则 DF 的长为_ 17. (2019伊春)一张直角三角形纸片ABC，90ACB，10AB，6AC ，
6、点D为BC边上 的任一点，沿过点D的直线折叠，使直角顶点C落在斜边AB上的点E处，当BDE是直角三 角形时，则CD的长为_ 三、解答题（本大题共三、解答题（本大题共 4 道小题）道小题） 18. 如图，在锐角三角形 ABC 中，点 D，E 分别在边 AC，AB 上，AGBC 于点 G，AFDE 于点 F，EAFGAC. (1)求证： ADEABC； (2)若 AD3，AB5，求AF AG的值 O D C B A F E D B CA 19. （2020丽水）如图，在ABC 中，AB42，B45 ，C60 （1）求 BC 边上的高线长 （2）点 E 为线段 AB 的中点，点 F 在边 AC 上，
7、连结 EF，沿 EF 将AEF 折叠得到PEF 如图 2，当点 P 落在 BC 上时，求AEP 的度数 如图 3，连结 AP，当 PFAC 时，求 AP 的长. 20. 已知：在等边ABC 中，D、E 分别是 AC、BC 上的点，且BAECBD60，DH AB，垂足为点 H. (1)如图，当点 D、E 分别在边 AC、BC 上时，求证：ABEBCD； (2)如图，当点 D、E 分别在 AC、CB 延长线上时，探究线段 AC、AH、BE 的数量关系； (3)在(2)的条件下，如图，作 EKBD 交射线 AC 于点 K，连接 HK，交 BC 于点 G，交 BD 于点 P，当 AC6，BE2 时，求
8、线段 BP 的长 21. 如图，四边形 ABCD 内接于圆 O，BAD90 ，AC 为直径，过点 A 作圆 O 的切线交 CB 的延长线于点 E，过 AC 的三等分点 F(靠近点 C)作 CE 的平行线交 AB 于点 G，连接 CG. (1)求证：ABCD； (2)求证：CD2BE BC； (3)当 CG 3，BE9 2，求 CD 的长 答案答案 一、选择题（本大题共一、选择题（本大题共 10 道小题）道小题） 1. 【答案】【答案】B 2. 【答案】【答案】B 解析DEBC， ADEABC， = ，即 2 3= 4 ，解得 BC=6，故选 B. 3. 【答案】【答案】B 解析根据勾股定理分别
9、表示出已知三角形的各边长，同理利用勾股定理表示出 四个选项中阴影三角形的各边长，利用三边长对应成比例的两个三角形相似可得结果， A1B1C1各边长分别为 1，2，5，选项 A 中阴影三角形三边长分别为:2，5，3，三边不 与已知三角形各边对应成比例， 故两三角形不相似;选项 B 中阴影三角形三边长分别为:2， 2， 10，三边与已知三角形的各边对应成比例，故两三角形相似;选项 C 中阴影三角形三边长分 别为:1，5，22，三边不与已知三角形各边对应成比例，故两三角形不相似;选项 D 中阴影 三角形三边长分别为:2， 5，13， 三边不与已知三角形各边对应成比例， 故两三角形不相似， 故选 B.
10、 4. 【答案】【答案】D 解析因为四边形 ABCD 是平行四边形，所以 AD=BC.因为 DEAD=13，F 为 BC 中点， 所以 DECF=23， 因为平行四边形 ABCD 中， DECF， 所以 DEGCFG， 相似比为 23，所以 S DEGS CFG=49.故选 D. 5. 【答案】【答案】A 【解析】由 ab=34 知，所以 34ba 4 3 a b 所以由得到：， 解得所以 所以故选 A 6. 【答案】【答案】C 【解析】本题考查菱形的性质、相似三角形的性质、函数的图象和二次函数的图 象和性质. 解题思路： 设 AC、 BD 交于点 O， 由于点 P 是菱形 ABCD 的对角线
11、 AC 上一动点， 所以 0 x2.当 0 x1 时，AMNABDAP AO MN BD x 1 MN 1 MNxy1 2x 2.此二次函 数的图象开口向上， 对称轴是 x0， 此时 y 随 x 的增大而增大. 所以 B 和 D 均不符合条件 当 1x2 时，CMNCBDCP CO MN BD 2x 1 MN 1 MN2xy1 2x(2x) 1 2x 2x.此 二次函数的图象开口向下，对称轴是 x1，此时 y 随 x 的增大而减小. 所以 A 不符合条件 综 上所述，只有 C 是符合条件的 7. 【答案】【答案】A 解析如图所示.设 DM=x，则 CM=8-x， 根据题意得:1 2(8-x+8
12、) 3 3=3 3 6，解得 x=4，DM=4. D=90 . 由勾股定理得: BM=2+ 2=42+ 32=5. 过点 B 作 BH水平桌面于 H，HBA+ABM=ABM+DBM=90 ， HBA=DBM， AHB=D=90 ， ABHMBD， = ，即 8 =3 5，解得 BH= 24 5 ，即水面高度为24 5 . 8. 【答案】【答案】A 【解析】利用平行截割定理求 CE CA 的值DEAB， CE AE = CD BD = 3 2 ，CE+AE=AC， CE CA = 3 5 9. 【答案】【答案】D 【解析】A（1,2）,B（1,1），C（3,1），AB=1，BC=2,AC= 5.
13、DEF与ABC成位似 图形，且相似比为2，DF=2AB=2 14a b 4 14 3 a a 6a8b 22 6 84a b 10. 【答案】【答案】C 【解析】设， ， ， ， ， ， ， 设， ， 故选 C 二、填空题（本大题共二、填空题（本大题共 7 道小题）道小题） 11. 【答案】【答案】 【解析】， 故 2y=x，则，故答案为： 12. 【答案】【答案】 3 2 【解析】点D，E分别是边AB，AC的中点， 1 /, 2 DE BC DEBC ADEABC 2 1 () 4 ADE ABC SDE SBC ，即4 ABCADE SS 2ADxBDx3ABx DEBCADEABC DE
14、ADAE BCABAC 2 63 DEx x 4DE 2 3 AE AC ACDBADEB ADEACD AA ADEACD ADAEDE ACADCD 2AEy3ACy 2 3 ADy yAD 6ADy 24 6 y CDy 2 6CD 1 2 3 2 xy x 223xyx 1 2 y x 1 2 又 1 2 ADE S， 1 42 2 ABC S 则四边形DBCE的面积为 13 2 22 ABCADE SS. 故答案为： 3 2 13. 【答案】【答案】（ ，2） 【解析】将AOB 以点 O 为位似中心，为位似比作位似变换，得到A1OB1，A（2，3） ， 点 A1的坐标是： （ 2，
15、3） ，即 A1（，2） 故答案为： （，2） 14. 【答案】【答案】(4，8)或(4，8) 【解析】ABC 和A1B1C1 的相似比等于 1 2，A1B1C1 和ABC 的相似比等于 2因 此将点 A(2，4)的横、纵坐标乘以2 即得点 A1 的坐标，点 A1 的坐标是(4，8)或(4， 8) 15. 【答案】【答案】 3 32 【解析】法 1：过 B 点作 BE/AD 交 AC 于点 E，则ADOEBO，由DAC90 ，得到 BE AD， AO OE OD OB 3 4，由 tanACB 1 2，可得 CE2BE4AE， S ABD SCBD AO OC 3 4(34)4 3 32 法
16、2：如图，过点 D 作 DMBC，交 CA 的延长线于点 M，延长 BA 交 DM 于点 N，得到ABC ANM，OBCODM，进而得出对应边成比例，AB BC AN NMtanACB 1 2， BC DM OB OD 4 3；又ABCDAC90 ，BACNAD90 ，BACBCA90 ，NAD BCA，ABCDAN，得出对应边之间关系，AB BC DN NA 1 2，设 ABa，DNb，则 O D C B A E BC2a，NA2b，MN4b，得 DM3 2a，4bb 3 2a，即 b 3 10a，进而表示三角形的面积， 得到S ABD SCBD 1 2ABDN 1 2BCNB ab 2a(
17、a2b) 3 10a 2 2a16 10a 3 32 16. 【答案】【答案】 54 85 【解析】本题考查平行线分线段成比例定理，相似三角形的判定与性质已知ACB90 ， AC3， BC4， 由勾股定理， 得 AB5 CDAB， 由三角形的面积， 得 CD AC BC AB 12 5 易 得 ABCACDCBD， 由相似三角形对应边成比例， 得 AD AC AC AB 9 5 ， BD BC BC AB 16 5 过点 E 作 EGAB 交 CD 于点 G， 由平行线分线段成比例， 得 DG 1 2 CD 6 5 ， EG 8 5 ， 所以 DFAD GFEG ，即 9 5 68 55 DF
18、 DF ，所以 DF，故答案为 54 85 17. 【答案】【答案】3或 24 7 【解析】分两种情况： 若90DEB，则90AEDC，CDED， 连接AD，则RtRtACDEAD， G F E D B CA 6AEAC，10 64BE ， 设CDDEx，则8BDx ， RtBDE中， 222 DEBEBD， 222 4(8)xx， 解得3x ，3CD； 若90BDE，则90CDEDEFC，CDDE， 四边形CDEF是正方形，90AFEEDB，AEFB ， AEFEBD， AFEF EDBD ， 设CDx，则EFDFx，6AFx ，8BDx ， 6 8 xx xx ，解得 24 7 x ， 2
19、4 7 CD ， 综上所述，CD的长为3或 24 7 ，故答案为：3或 24 7 三、解答题（本大题共三、解答题（本大题共 4 道小题）道小题） 18. 【答案】【答案】 【思维教练】(1)要证 ADEABC，现已知EADCAB，故只需找另一组对角相等或 夹角的两边对应成比例 由题干条件易知EAFGAC， AFEAGC， 故 AEFACG， AEFC， 由两角对应相等即可得证； (2)由(1)中的结论， 利用相似三角形的性质求解即可 (1)证明：在 ABC 中，AGBC 于点 G，AFDE 于点 F， AFEAGC90 ， 在 AEF 和 ACG 中， AFEAGC，EAFGAC， AEFAC
20、G，AEFC.(2 分) 在 ADE 和 ABC 中， AEDC，EADCAB， ADEABC；(4 分) (2)解：由(1)知 ADEABC， AD AB AE AC 3 5，(6 分) 又AEFACG，AF AG AE AC 3 5.(8 分) 19. 【答案】【答案】 解： （1）如图 1 中，过点 A 作 ADBC 于 D 在 RtABD 中，ADABsin4544 （2）如图 2 中， AEFPEF， AEEP， AEEB， BEEP， EPBB45 ， PEB90 ， AEP180 90 90 如图 3 中，由（1）可知：AC， PFAC，PFA90 ，AEFPEF，AFEPFE4
21、5 ， AFEB，EAFCAB，AEFACB， AF AB = AE AC，即 AF 42 = 22 83 3 ，AF23，在 RtAFP，AFFP， AP= 2AF26 20. 【答案】【答案】 (1)证明：证明：ABC 为等边三角形， ABCCCAB60，ABBC， 在ABE 和BCD 中， BAECBD ABBC ABEBCD ， ABEBCD(ASA)； (2)解：解：ABC 为等边三角形， ABCCAB60，ABBC， ABEBCD18060120. 在ABE 和BCD 中， BAECBD ABBC ABEBCD ， ABEBCD(ASA)， BECD. DHAB， DHA90， C
22、AB60， ADH30， AD2AH， ACADCD2AHBE； (3)解：解：如解图，作 DSBC 延长线于点 S，作 HMAC 交 BC 于点 M， 解图 AC6，BE2， 由(2)得 AH4，BH2, 与(1)同理可得 BECD2，CE8， SCDACB60， CDS30， CS1，SD 3，BS7， BD2BS2SD272(3)2， BD2 13， EKBD， CBDCEK， CB CE CD CK BD EK， CKCDCE CB 28 6 8 3，EK CEBD CB 82 13 6 8 13 3 . HMAC， HMBACB60， HMB 为等边三角形，BMBHHM2， CMCB
23、BM4， 又HMAC， HMGKCG， HM KC MG CG， 即 3 8 2 MG 4MG，MG 12 7 ，BG26 7 ，EG40 7 ， EKBD， GBPGEK， BP EK GB GE， BP26 13 15 . 21. 【答案】【答案】 (1)证明：AC 为直径， ABCADC90 ， ABCBAD90 ， BCAD， BCACAD， 又ACCA， ABCCDA(AAS)， ABCD； (2)证明：AE 为O 的切线且 O 为圆心， OAAE， 即 CAAE， EABBAC90 ， 而BACBCA90 ， EABBCA， 而EBAABC， EBAABC， EB AB BA BC， AB2BE BC， 由(1)知 ABCD， CD2BE BC； (3)解：由(2)知 CD2BE BC， 即 CD29 2BC， FGBC 且点 F 为 AC 的三等分点， G 为 AB 的三等分点， 即 CDAB3BG， 在 Rt CBG 中，CG2BG2BC2， 即 3(1 3CD) 2BC2， 将代入，消去 CD 得， BC21 2BC30， 即 2BC2BC60， 解得 BC3 2或 BC2(舍)， 将代入得，CD3 3 2 .
