1、2021 中考数学专题训练中考数学专题训练：等腰三角形等腰三角形 一、选择题（本大题共一、选择题（本大题共 10 道小题）道小题） 1. 若等腰三角形的顶角为 50 ，则它的底角度数为 ( ) A.40 B.50 C.60 D.65 2. 如图所示，线段 AC 的垂直平分线交线段 AB 于点 D，A=50 ，则BDC= ( ) A.50 B.100 C.120 D.130 3. （2020 福建）如图，AD是等腰三角形ABC的顶角平分线，5BD，则CD等于（ ） A.10 B.5 C.4 D.3 4. 如图，在ABC 中，ABAC5，BC6，点 M 为 BC 的中点，MNAC 于点 N，则 M
2、N 等于( ) A. 6 5 B. 9 5 C. 12 5 D. 16 5 5. (2019梧州)如图，DE是ABC的边AB的垂直平分线，D为垂足，DE交AC于点E，且 85ACBC， ，则BEC的周长是 A12 B13 C14 D15 6. （2020 河南）如图，在ABC中，AB=BC=3，BAC=30 ，分别以点A，C为圆心，AC的 长为半径作弧，两弧交于点D，连接DA，DC，则四边形ABCD的面积为( ) A.6 3 B.9 C.6 D. 3 3 7. 如图，在五边形 ABCDE 中，ABACADAE，且 ABED，EAB120 ，则BCD 的 度数为( ) A150 B160 C13
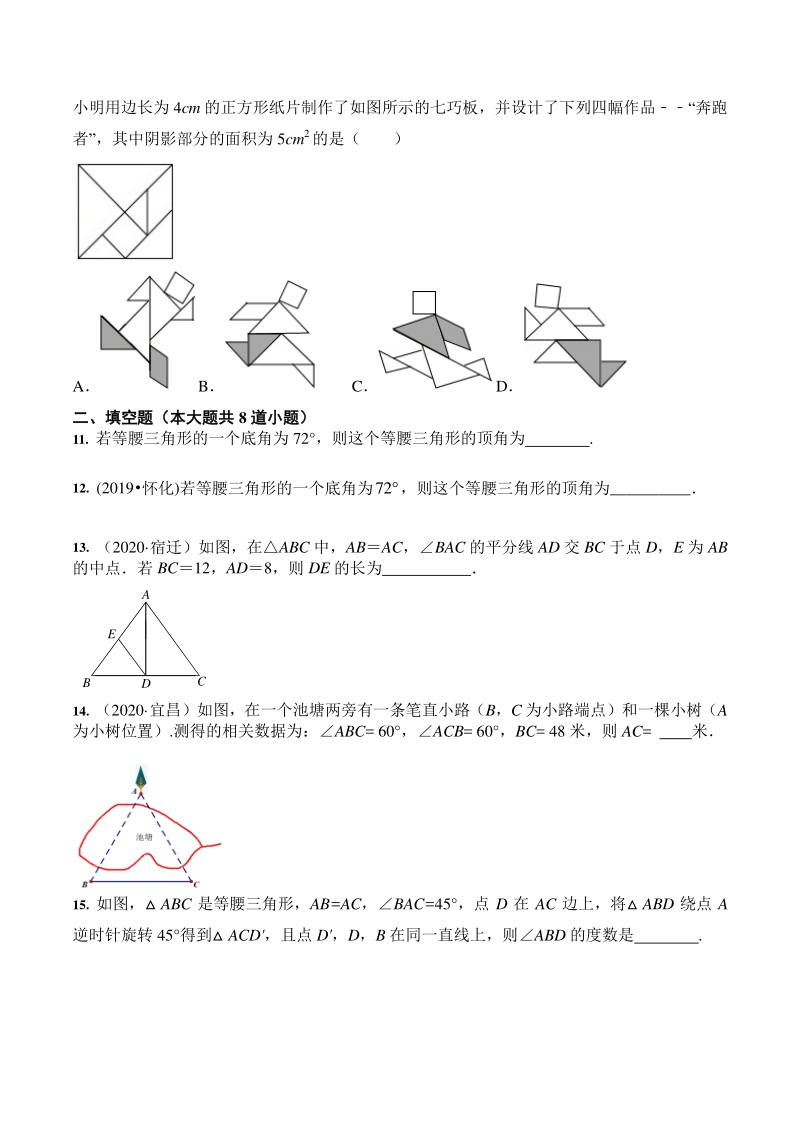
3、0 D60 8. (2020 荆门)如图 3，ABC 中，ABAC，BAC120 ，BC23，D 为 BC 的中点，AE 1 4 AB，则EBD 的面积为( ) A 3 3 4 B 3 3 8 C 3 4 D 3 8 9. (2019广西)如图， 在ABC中，,40ACBCA， 观察图中尺规作图的痕迹， 可知BCG 的度数为 A40 B45 C50 D60 10. （2020 烟台）七巧板是我们祖先的一项创造，被誉为“东方魔板”在一次数学活动课上， D E C A B 小明用边长为 4cm 的正方形纸片制作了如图所示的七巧板，并设计了下列四幅作品“奔跑 者”，其中阴影部分的面积为 5cm2的是
4、（ ） AB C D 二、填空题（本大题共二、填空题（本大题共 8 道小题）道小题） 11. 若等腰三角形的一个底角为 72 ，则这个等腰三角形的顶角为 . 12. (2019怀化)若等腰三角形的一个底角为72，则这个等腰三角形的顶角为_ 13. （2020 宿迁）如图，在ABC 中，ABAC，BAC 的平分线 AD 交 BC 于点 D，E 为 AB 的中点若 BC12，AD8，则 DE 的长为 14. （2020 宜昌）如图，在一个池塘两旁有一条笔直小路（B，C 为小路端点）和一棵小树（A 为小树位置）.测得的相关数据为：ABC= 60 ，ACB= 60 ，BC= 48 米，则 AC= 米
5、15. 如图， ABC 是等腰三角形，AB=AC，BAC=45 ，点 D 在 AC 边上，将 ABD 绕点 A 逆时针旋转 45 得到 ACD，且点 D，D，B 在同一直线上，则ABD 的度数是 . E D C B A 16. （2020 贵阳） （4 分）如图，ABC 中，点 E 在边 AC 上，EBEA，A2CBE，CD 垂直于 BE 的延长线于点 D，BD8，AC11，则边 BC 的长为 17. （2020 湖北孝感） 某型号飞机的机翼形状如图所示， 根据图中数据计算 AB 的长为_ 米 （结果保留根号） 18. 如图，在 ABC 中，若 ABAC8，A30 ，则 S ABC_ 三、解答
6、题（本大题共三、解答题（本大题共 6 道小题）道小题） 19. 如图，在 ABC 中，AB=AC，ADBC 于点 D. (1)若C=42 ，求BAD 的度数; (2)若点 E 在边 AB 上，EFAC 交 AD 的延长线于点 F.求证:AE=FE. 20. （2020 广东）如题20图，在ABC中，点D、E分别是AB、AC边上的点，BD=CE，ABE= ACD，BE与CD相交于点F求证：ABC是等腰三角形 21. 如图，在 ABC 中，ABAC，ABC60 ，延长 BA 至点 D，延长 CB 至点 E，使 BE AD，连接 CD，AE，延长 EA 交 CD 于点 G. (1)求证： ACECB
7、D； (2)求CGE 的度数 22. 如图，已知BE、CF分别为ABC中B、C的平分线，AMBE于M，ANCF于N， 求证：MNBC 23. 如图，已知等腰直角三角形 ABC，点 P 是斜边 BC 上一点(不与 B，C 重合)，PE 是 ABP 的外接圆O 的直径 (1)求证： APE 是等腰直角三角形； (2)若O 的直径为 2，求 PC2PB2的值 F E C A B D N M E F C B A 24. 如图，AB 为O 的直径，C 为圆外一点，AC 交O 于点 D，BC2CD CA，ED BD ，BE 交 AC 于点 F. (1)求证：BC 为O 的切线； (2)判断 BCF 的形状
8、并说明理由； (3)已知 BC15，CD9，BAC36 ，求BD 的长度(结果保留 ). 答案答案 一、选择题（本大题共一、选择题（本大题共 10 道小题）道小题） 1. 【答案】【答案】D 2. 【答案】【答案】B 3. 【答案】【答案】B 【解析】本题考查了等腰三角形三线合一的性质，AD是等腰三角形ABC的顶角平分线， 5BD，CD=BD=5，因此本题选 B 4. 【答案】【答案】C 【解析】此题应首先连接 AM，则 AMBC. AM AC2CM24，然后由 三角形面积： SACM1 2AMCM.SACM 1 2ACMN.得： AMCMACMN.MN 12 5 .也可 以利用ACMMCN.
9、得：AC CM AM MN.MN AMCM AC 12 5 . 5. 【答案】【答案】B 【解析】DE是ABC的边AB的垂直平分线，AEBE， 85ACBC， ，BEC 的周长是：13BEECBCAEECBCACBC故选 B 6. 【答案】【答案】D 【解析】分别以点A、C为圆心，AC的长为半径作弧，两弧交于点D， AD=AC=CD，ACD是等边三角形，DAC=60 . AB=BC，AD=CD，连接BD交AC于点E，BD垂直平分AC，AEB=90 . BAC=30 ， AB= 3，BE= 3 2 ，AE= 3 2 ，AC=3 在RtADE中，DAC=60 ，AED=90 ，AE= 3 2 ，D
10、E= 3 3 2 ，BD= 33 32 3 22 +=， 四边形ABCD的面积为：33332 2 1 7. 【答案】【答案】A 解析 ABED， E180 EAB180 120 60 . 又ADAE， ADE 是等边三角形 EAD60 .BADEABEAD120 60 60 .ABACAD，B ACB， ACDADC.在四边形 ABCD中， BCDBADC1 2(360 BAD) 1 2 (360 60 )150 . 故选 A. 8. 【答案】【答案】B 【解析】连结 ADBC 1 2 (180 A)30 由等腰三角形的“三线合一”可知 AD BCADBD tanB3 3 3 1SABC 1
11、2 BC AD 1 2 23 13AE 1 4 AB，S EBD 3 4 SABD 3 8 SABC 3 3 8 故选 B 9. 【答案】【答案】C 【解析】由作法得CGAB，ABAC，CG平分ACB，AB ， 1804040100ACB， 1 50 2 BCGACB故选 C 10. 【答案】【答案】最小的等腰直角三角形的面积= 1 8 脳 1 2 脳421（cm2） ，平行四边形面积为 2cm2，中 等的等腰直角三角形的面积为 2cm2，最大的等腰直角三角形的面积为 4cm2，则 A、阴影部分的面积为 2+24（cm2） ，不符合题意； B、阴影部分的面积为 1+23（cm2） ，不符合题意
12、； C、阴影部分的面积为 4+26（cm2） ，不符合题意； D、阴影部分的面积为 4+15（cm2） ，符合题意 故选：D 二、填空题（本大题共二、填空题（本大题共 8 道小题）道小题） 11. 【答案】【答案】36 解析等腰三角形的一个底角为 72 ， 这个等腰三角形的顶角为 180 -72 2=36 . 12. 【答案】【答案】36 【解析】等腰三角形的一个底角为72，等腰三角形的顶角180727236， 故答案为：36 13. 【答案】【答案】5 【解析】 ABAC， BAC 的平分线 AD 交 BC 于点 D， ADBC， BDCD 1 2 BC6 在 RtABD 中， 由勾股定理，
13、 得 AB 22 68 10 又E 为 AB 的中点， DE 1 2 AB5 故 答案为 5 14. 【答案】【答案】48 【解析】 ABC=60 ， ACB=60 ， A=180 60 60 =60 ， ABC 是等边三角形， AB=BC=AC，BC=48，AC=48 15. 【答案】【答案】22.5 解析根据题意可知 ABDACD，BAC=CAD=45 ，AD=AD， ADD=ADD=180-45 2 =67.5 . D，D，B 三点在同一直线上， ABD=ADD-BAC=22.5 . 16. 【答案】【答案】45 【解析】 解： 延长 BD 到 F， 使得 DFBD， CDBF， BCF
14、 是等腰三角形， BCCF， 过点 C 点作 CHAB，交 BF 于点 HABDCHD2CBD2F，HFHC， BD8，AC11，DHBHBDACBD3，HFHC835， 在 RtCDH，由勾股定理可知：CD4，在 RtBCD 中，BC= 82+ 42=45， 故答案为：45 17. 【答案】【答案】（ 5 3 3 -1.6） 【解析】如图，过点 A 作 AMCM 于 M，则 CM=5m，在 RtBCM 中，BCM30 ,所以 BM=CM tan30 = 5 3 3 .由题意可知DCN 是等腰直角三角形，所以 CN=CD=3.4m,所以 MN=5-3.4=1.6(m),因为AMN 是等腰直角三
15、角形，所以 MN=AM=1.6m，所以 AB=BM-AM= （ 5 3 3 -1.6）m.故答案为（ 5 3 3 -1.6） 18. 【答案】【答案】16 解析 如图，过点 C 作 CDAB，垂足为 D， 则 ADC 是含 30 角的直角三角形，那么 DC1 2AC4，S ABC 1 2AB DC 1 2 8 416. 三、解答题（本大题共三、解答题（本大题共 6 道小题）道小题） 19. 【答案】【答案】 解:(1)(方法一):AB=AC，C=42 ， B=C=42 ， BAC=180 -B-C=180 -42 -42 =96 . ADBC， BAD=1 2BAC= 1 2 96 =48 .
16、 (方法二):AB=AC，C=42 ， B=C=42 . ADBC 于点 D，ADB=90 ， BAD=180 -90 -42 =48 . (2)证明:EFAC，CAF=F， AB=AC，ADBC，CAF=BAF， F=BAF，AE=FE. 20. 【答案】【答案】 证明：在BFD 和CFE 中，ABE=ACD，DFB=CFE，BD=CE， BFDCFE（AAS）.DBF=ECF.ABE=ACDDBF+ABE=ECF+ ACD. ABC=ACB. AB=AC. ABC 是等腰三角形. 【解析】先利用三角形边边角的判定方法证明DBF=ECF，再根据等式的性质，加上相等 角得到ABC=ACB，等角
17、对等边，得到 AB=AC.根据等腰三角形定义得到 ABC 是等腰 三角形. 21. 【答案】【答案】 解：(1)证明：ABAC，ABC60 ， ABC 是等边三角形 ABCBAC，ACBABC60 . BEAD，BEBCADAB， 即 CEBD. 在 ACE 和 CBD 中， CEBD， ACECBD， ACCB， ACECBD(SAS) (2)由(1)知 ACECBD，ED. BAEDAG， EBAEDDAG， 即CGEABC. ABC60 ， CGE60 . 22. 【答案】【答案】 延长AM、AN交BC于点Q、R 由等腰三角形三线合一可得AMQM、ANRN 再由三角形中位线可得MNBC
18、23. 【答案】【答案】 【思路分析】(1)因为 PE 是直径，所以PAE90 ，要证 PAE 是等腰直角三角形，只要证 PAEA， 由已知得PBA45 ， 而PEA 与PBA 是同弧所对的圆周角， 所以PEAPBA， 问题得证；(2)由(1)得 PACEAB，所以 PCBE，因为 PE 是直径，所以PBE90 ，所 以 PC2PB2BE2PB2PE24. 解图 (1)证明：如解图，ABC 是等腰直角三角形， ACAB，CAB90 ，PBA45 ， 在O 中，PEA 与PBA 都是AP 所对的圆周角， PEAPBA45 ， PE 为O 的直径， PAE90 ，(4 分) PAE 为等腰直角三角
19、形且 APAE；(5 分) (2)PAECAB90 ， CABPABPAEPAB， CAPBAE， CAPBAE(SAS)，(8 分) CABE45 ， PBEPBAABE90 (10 分) 在 Rt PBE 中，PC2PB2PE24.(12 分) 24. 【答案】【答案】 (1)证明：证明：BC2CD CA， BC CA CD BC， CC， CBDCAB， CBDBAC， 又AB 为O 的直径， ADB90 ， 即BACABD90 ， ABDCBD90 ， 即 ABBC， 又AB 为O 的直径， BC 为O 的切线； (2)解：解： BCF 为等腰三角形 证明如下：ED BD ， DAEBAC， 又CBDCAB， BACCBD， CBDDAE， DAEDBF， DBFCBD， BDF90 ， BDCBDF90 ， BDBD， BDFBDC， BFBC， BCF 为等腰三角形； (3)解：解：由(1)知，BC 为O 的切线， ABC90 BC2CD CA， ACBC 2 CD 152 9 25， 由勾股定理得 AB AC2BC225215220， O 的半径为 rAB 2 10， BAC36 ， BD 所对圆心角为 72 . 则BD 7210 180 4.
