1、第第 4 章几何图形初步解答题精选章几何图形初步解答题精选 1 （2019 秋西城区期末）对于平面内给定射线 OA，射线 OB 及MON，给出如下定义：若由射线 OA、 OB 组成的AOB 的平分线 OT 落在MON 的内部或边 OM、 ON 上， 则称射线 OA 与射线 OB 关于MON 内含对称例如，图 1 中射线 OA 与射线 OB 关于MON 内含对称 已知：如图 2，在平面内，AOM10，MON20 （1）若有两条射线 OB1，OB2的位置如图 3 所示，且B1OM30，B2OM15，则在这两条射线 中，与射线 OA 关于MON 内含对称的射线是 ； （2）射线 OC 是平面上绕点
2、O 旋转的一条动射线，若射线 OA 与射线 OC 关于MON 内含对称，设 COMx，求 x 的取值范围； （3）如图 4，AOEEOH2FOH20，现将射线 OH 绕点 O 以每秒 1的速度顺时针旋转， 同时将射线 OE 和 OF 绕点 O 都以每秒 3的速度顺时针旋转设旋转的时间为 t 秒，且 0t60若 FOE 的内部及两边至少存在一条以 O 为顶点的射线与射线 OH 关于MON 内含对称， 直接写出 t 的取值 范围 2 （2020 春东城区校级期末）已知：如图，O 是直线 AB 上的一点，COD90，OC 平分AOE， BOD30，求DOE 的度数 3 （2019 秋密云区期末）如图
3、，点 O 在直线 AB 上，OC 是AOD 的平分线 （1）若BOD50，则AOC 的度数为 （2）设BOD 的大小为 ，求AOC（用含 的代数式表示） （3）作 OEOC，直接写出EOD 与EOB 之间的数量关系 4 （2019 秋北京期末）如图，请度量出需要的数据，并计算阴影部分的面积 5 （2019 秋通州区期末）如图，以直线 AB 上一点 O 为端点作射线 OC，使AOC70，在同一个平面 内将一个直角三角板的直角顶点放在点 O 处 （注：DOE90） （1）如图 1，如果直角三角板 DOE 的一边 OD 放在射线 OA 上，那么COE 的度数为 ； （2）如图 2，将直角三角板 DO
4、E 绕点 O 按顺时针方向转动到某个位置，如果 OC 恰好平分AOE，求 COD 的度数； （3）如图 3，将直角三角板 DOE 绕点 O 任意转动，如果 OD 始终在AOC 的内部，请直接用等式表示 AOD 和COE 之间的数量关系 6 （2019 秋海淀区期末）阅读下面材料： 小聪遇到这样一个问题：如图 1，AOB，请画一个AOC，使AOC 与BOC 互补 小聪是这样思考的：首先通过分析明确射线 OC 在AOB 的外部，画出示意图，如图 2 所示：然后通过 构造平角找到AOC 的补角COD， 如图 3 所示：进而分析要使AOC 与BOC 互补，则需BOCCOD 因此，小聪找到了解决问题的方
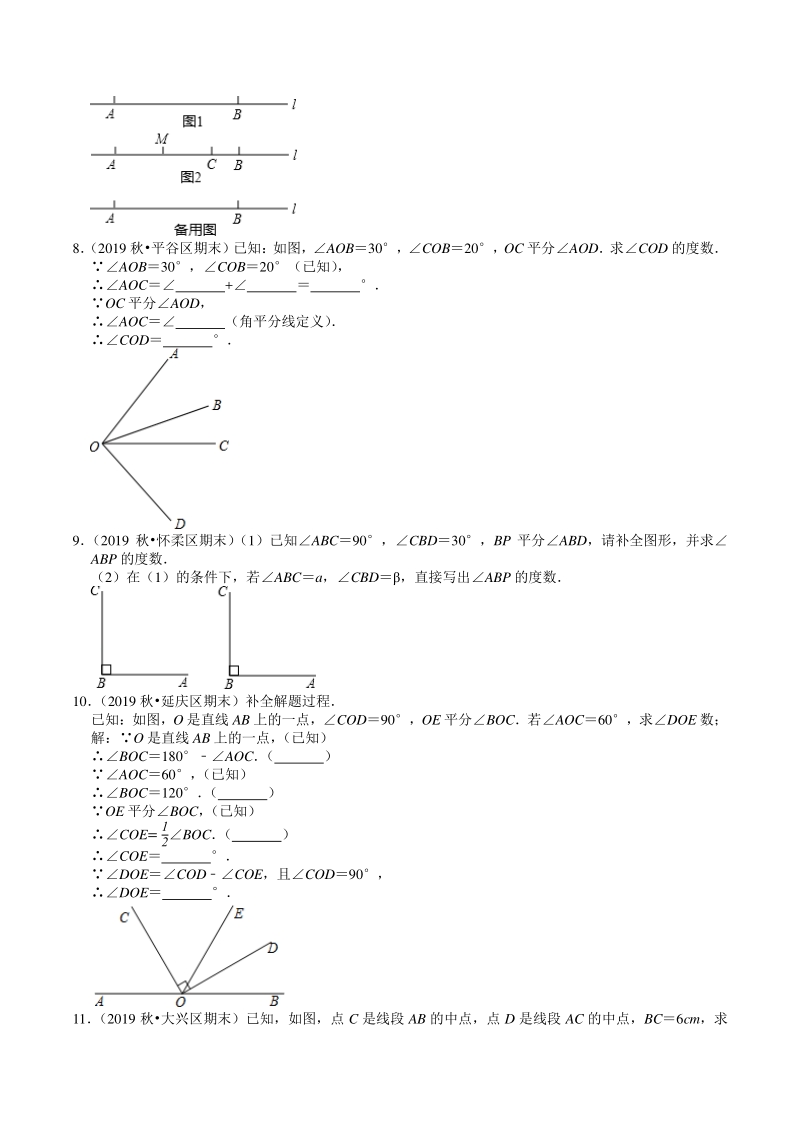
5、法：反向延长射线 OA 得到射线 OD，利用量角器画出BOD 的平分线 OC，这样就得到了BOC 与AOC 互补 （1）小聪根据自己的画法写出了已知和求证，请你完成证明： 已知：如图 3，点 O 在直线 AD 上，射线 OC 平分BOD 求证：AOC 与BOC 互补 （2）参考小聪的画法，请在图 4 中画出一个AOH，使AOH 与BOH 互余 （保留画图痕迹） （3）已知EPQ 和FPQ 互余，射线 PM 平分EPQ，射线 PN 平分FPQ若EPQ（0 90） ，直接写出锐角MPN 的度数是 7 （2019 秋门头沟区期末）阅读材料，并回答问题： 材料：数学课上，老师给出了如下问题 已知，点
6、A、B、C 均在直线 l 上，AB8，BC2，M 是 AC 的中点，求 AM 的长 小明的解答过程如下： 解：如图 2， AB8，BC2， ACABBC826 M 是 AC 的中点， AM= 1 2 = 1 2 63（） 小芳说： “小明的解答不完整” 问题： （1）小明解答过程中的“”为 ； （2）你同意小芳的说法吗？如果同意，请将小明的解答过程补充完整；如果不同意，请说明理由 8 （2019 秋平谷区期末）已知：如图，AOB30，COB20，OC 平分AOD求COD 的度数 AOB30，COB20（已知） ， AOC + OC 平分AOD， AOC （角平分线定义） COD 9 （2019
7、 秋怀柔区期末） （1）已知ABC90，CBD30，BP 平分ABD，请补全图形，并求 ABP 的度数 （2）在（1）的条件下，若ABCa，CBD，直接写出ABP 的度数 10 （2019 秋延庆区期末）补全解题过程 已知：如图，O 是直线 AB 上的一点，COD90，OE 平分BOC若AOC60，求DOE 数； 解：O 是直线 AB 上的一点， （已知） BOC180AOC （ ） AOC60， （已知） BOC120 （ ） OE 平分BOC， （已知） COE= 1 2BOC （ ） COE DOECODCOE，且COD90， DOE 11 （2019 秋大兴区期末）已知，如图，点 C
8、是线段 AB 的中点，点 D 是线段 AC 的中点，BC6cm，求 线段 BD 的长 请将以下求解过程补充完整： 因为点 C 是线段 AB 的中点， 所以 ， 因为 BC6cm， 所以 AC cm， 因为点 D 是线段 AC 的中点， 所以 DC 所以 DC cm 所以 BD cm 12 （2019 秋石景山区期末） 已知： 射线 OC 在AOB 的内部， AOC： BOC8： 1， COD2COB， OE 平分AOD （1）如图，若点 A，O，B 在同一条直线上，OD 是AOC 内部的一条射线，请根据题意补全图形，并 求COE 的度数； （2）若BOC（018） ，直接写出COE 的度数（用
9、含 的代数式表示） 13 （2019 秋东城区期末）根据题意，补全解题过程： 如图，AOB90，OE 平分AOC，OF 平分BOC求EOF 的度数 解：因为 OE 平分AOC，OF 平分BOC 所以EOC= 1 2AOC，FOC= 1 2 所以EOFEOC = 1 2（AOC ） = 1 2 14 （2019 秋昌平区期末）已知线段 AB，点 C 在直线 AB 上，D 为线段 BC 的中点 （1）若 AB8，AC2，求线段 CD 的长 （2）若点 E 是线段 AC 的中点，直接写出线段 DE 和 AB 的数量关系是 15 （2019 秋西城区期末）24、已知：如图，O 是直线 AB 上一点，O
10、D 是AOC 的平分线，COD 与 COE 互余求证：AOE 与COE 互补 请将下面的证明过程补充完整： 证明：O 是直线 AB 上一点 AOB180 COD 与COE 互余 COD+COE90 AOD+BOE OD 是AOC 的平分线 AOD （理由： ） BOECOE（理由： ） AOE+BOE180 AOE+COE180 AOE 与COE 互补 16 （2019 秋丰台区期末）如图，货轮 O 在航行过程中，发现灯塔 A 在它北偏东 60的方向上，同时，在 它南偏西 20、 西北 （即北偏西 45） 方向上又分别发现了客轮 B 和海岛 C， 仿照表示灯塔方位的方法， 画出表示客轮 B 和
11、海岛 C 方向的射线 17 （2019 秋丰城市期末）已知正方体的展开图如图所示，如果正方体的六个面分别用字母 A，B，C，D， E，F 表示，当各面上的数分别与它对面的数互为相反数，且满足 B1，Ca22a+1，D1，E 3a+4，F2a 时，求 A 面表示的数值 18 （2019 秋丰润区期末）如图，O 是直线 AB 上的一点，COD 是直角，OE 平分BOC （1）若AOC30时，则DOE 的度数为 ； （2）将图中的COD 绕顶点 O 顺时针旋转至图的位置，其它条件不变，探究AOC 和DOE 的 度数之间的关系，写出你的结论，并说明理由； （3）将图中的COD 绕顶点 O 顺时针旋转至
12、图的位置，其他条件不变直接写出AOC 和DOE 的度数之间的关系： 19 （2019 秋门头沟区期末）已知：如图，OC 是AOB 的平分线 （1）当AOB60时，求AOC 的度数； （2）在（1）的条件下，过点 O 作 OEOC，请在图中补全图形，并求AOE 的度数； （3）当AOB 时，过点 O 作 OEOC，直接写出AOE 的度数 （用含 的代数式表示） 20 （2018 秋延庆区期末）如图，点 O 是直线 AB 上一点，BOC120，OD 平分AOC （1）求COD 的度数 请你补全下列解题过程 点 O 为直线 AB 上一点， AOB BOC120， AOC OD 平分AOC， COD=
13、 1 2AOC COD （2）若 E 是直线 AB 外一点，满足COE：BOE4：1，直接写出BOE 的度数 21 （2018 秋密云区期末）已知：如图，AC2BC，D 为 AB 中点，BC3，求 CD 的长 请你补全下面的解题过程： 解：AC2BC，BC3 AC ABAC+BC BD= 1 2 CDBDBC 22 （2018 秋石景山区期末）已知：如图，点 C 在线段 AB 上，点 M、N 分别是 AC、BC 的中点 （1）若 AC8，CB6，求线段 MN 的长； （2）若 ACa，MNb，则线段 BC 的长用含 a，b 的代数式可以表示为_ 解： （1）AC8，CB6， ABAC+CB14
14、 点 M、N 分别是 AC、BC 的中点， MC AC，NC BC ， （填推理依据） MN （2）线段 BC 的长用含 a，b 的代数式可以表示为 23 （2018 秋丰台区期末）如图，CAB+ABC90，AD 平分CAB，与 BC 边交于点 D，BE 平分 ABC 与 AC 边交于点 E （1）依题意补全图形，并猜想DAB+EBA 的度数等于 ； （2）证明以上结论 证明：AD 平分CAB，BE 平分ABC， DAB= 1 2CAB， EBA （理由： ） CAB+ABC90， DAB+EBA （ + ） 24 （2018 秋昌平区期末）补全解题过程 已知：如图，AOB40，BOC60，O
15、D 平分AOC 求BOD 的度数 解：AOCAOB+ ， 又AOB40，BOC60， AOC OD 平分AOC， AOD AOC（ ） AOD50 BODAOD BOD 25 （2018 秋平谷区期末）已知直线 AB 上一点 O，以 O 为端点画射线 OC，作AOC 的角平分线 OD，作 BOC 的角平分线 OE； （1）按要求完成画图； （2）通过观察、测量你发现DOE ； （3）补全以下证明过程： 证明：OD 平分AOC（已知） DOCAOC OE 平分BOC（已知） EOCBOC AOC+BOC DOEDOC+EOC（AOC+BOC） 26 （2018 秋房山区期末）填空，完成下列说理过
16、程： O 是直线 AB 上一点，COD90，OE 平分BOC （1）如图 1，若AOC50，求DOE 的度数； 解：O 是直线 AB 上一点， AOC+BOC180 AOC50， BOC130 OE 平分BOC（已知） ， COE= 1 2BOC（ ） COE COD90，DOE DOE （2） 将图 1 中COD 按顺时针方向转至图 2 所示的位置， OE 仍然平分BOC， 试猜想AOC 与DOE 的度数之间的关系为： 27 （2018 秋北京期末）分类讨论是一种非常重要的数学方法，如果一道题提供的已知条件中包含几种情 况，我们可以分情况讨论来求解例如：若|x|3，|y|2 求 x+y 的值
17、 情况若 x3，y2 时，x+y5 情况若 x3，y2 时，x+y1 情况 若 x3，y2 时，x+y1 情况若 x3，y2 时，x+y5 所以，x+y 的值为 1，1，5，5 几何的学习过程中也有类似的情况： 如图，点 O 是直线 AB 上的一点，将一直角三角板如图摆放，过点 O 作射线 OE 平分BOC当直角三 角板绕点 O 继续顺时针旋转一周回到图 1 的位置时， 在旋转过程中你发现AOC 与DOE （0AOC 180，0DOE180）之间有怎样的数量关系？ 情况（1）如图 1，当 0AOD90时，若AOC40，则DOE 度数是 ； 情况（2）如图 2，当AOC 是钝角时，使得直角边 O
18、C 在直线 AB 的上方，若AOC160，其他条件 不变，则DOE 的度数是 ； 情况（3）若AOC，在旋转过程中你发现AOC 与DOE 之间有怎样的数量关系？请你直接用含 的代数式表示DOE 的度数； 28 （2018 秋通州区期末）如图是一个正方体的展开图，标注了字母 A，C 的面分别是正方体的正面和底 面，其他面分别用字母 B，D，E，F 表示已知 Akx+1，B3x2，C1，Dx1，E2x1，F x （1）如果正方体的左面与右面所标注字母代表的代数式的值相等，求出 x 的值； （2）如果正面字母 A 代表的代数式与对面字母代表的代数式的值相等，且 x 为整数，求整数 k 的值 29 （
19、2018 秋北京期末）如图，点 A，B，C 是平面上三个点 （1）按下列要求画图： 画线段 AB；画射线 CB；反向延长线段 AB；连接 AC （2）请你测量点 B 到直线 AC 的距离，大约是 cm （精确到 0.1cm） 30 （2018 秋顺义区期末）阅读材料并回答问题： 阅读材料： 数学课上，老师给出了如下问题： 如图 1，AOB120，OC 平分AOB若COD20，请你补全图形，并求BOD 的度数 以下是小明的解答过程： 解：如图 2， AOB120，OC 平分AOB BOC AOB COD20， BOD 小敏说： “我觉得这个题有两种情况，小明考虑的是 OD 在BOC 内部的情况，
20、事实上 OD 还可能在 AOC 的内部” 完成以下问题： （1）请你将小明的解答过程补充完整； （2）根据小敏的想法，请你在图 1 中画出另一种情况对应的图形，此时BOD 的度数为 31 （2018 秋海淀区期末）已知点 C 在线段 AB 上，点 M 为 AB 的中点，AC8，CB2 （1）如图 1，求 CM 的长； （2）如图 2，点 D 在线段 AB 上，若 ACBD，判断点 M 是否为线段 CD 的中点，并说明理由 32 （2018 秋朝阳区期末）填空，完成下列说理过程 如图，AOB90，COD90，OA 平分DOE，若BOC20，求COE 的度数 解：因为AOB90 所以BOC+AOC
21、90 因为COD90 所以AOD+AOC90 所以BOCAOD （ ） 因为BOC20 所以AOD20 因为 OA 平分DOE 所以 2AOD （ ） 所以COECODDOE 33 （2018 秋西城区期末）已知：如图，点 A，点 B，点 D 在射线 OM 上，点 C 在射线 ON 上，O+OCA 90，O+OBC90，CA 平分OCD 求证：ACDOBC 请将下面的证明过程补充完整： 证明：O+OCA90，O+OBC90， OCA （理由： ） CA 平分OCD ACD （理由： ） ACDOBC （理由： ） 34 （2018 秋门头沟区期末）填空，完成下列说理过程 如图，已知点 A，O，
22、B 在同一条直线上，OE 平分BOC，DOE90 求证：OD 是AOC 的平分线； 证明：如图，因为 OE 是BOC 的平分线， 所以BOECOE （ ） 因为DOE90 所以DOC+ 90 且DOA+BOE180DOE 所以DOC+ DOA+BOE 所以 所以 OD 是AOC 的平分线 第第 4 章几何图形初步解答题精选章几何图形初步解答题精选 参考答案与试题解析参考答案与试题解析 一解答题（共一解答题（共 34 小题）小题） 1 【解答】解： （1）AOB1在MON 的外部， 射线 OA、OB1组成的AOB1的平分线在MON 的外部， OB1不是与射线 OA 关于MON 内含对称的射线，
23、B2OM15，AOM10， AOB225， 射线 OA、OB2组成的AOB2的平分线在MON 的内部， OB2是与射线 OA 关于MON 内含对称的射线， 故答案为：OB2； （2）由（1）可知，当 OC 在直线 OA 的下方时，才有可能存在射线 OA 与射线 OC 关于MON 内含对 称， COMx，AOM10，MON20， AOC（x+10），AON30， 射线 OA 与射线 OC 关于MON 内含对称， 10 1 2（x+10）30， 10 x50； （3）AOEEOH2FOH20， HOM50，HON70，EOM30，FOM40， 若射线 OE 与射线 OH 关于MON 内含对称， 5
24、0t 330+50 2 70t， 20t30； 若射线 OF 与射线 OH 关于MON 内含对称， 50t 50+340 2 70t， 22.5t32.5， 综上所述：20t32.5 2 【解答】解：BOD30，COD90， AOC90BOD60 OC 平分AOE， COEAOE60 DOECODCOE30 3 【解答】解： （1）点 O 在直线 AB 上， AOD+BOD180， BOD50， AOD180BOD18050130， OC 是AOD 的平分线， AOC= 1 2AOD= 1 2 13065， 故答案为：65； （2）点 O 在直线 AB 上， AOD+BOD180， BOD，
25、AOD180BOD180， OC 是AOD 的平分线， AOC= 1 2AOD= 1 2 （180）90 1 2； （3）OE 在 AB 的上面，如图， OC 是AOD 的平分线， DOCAOC= 1 2AOD， OCOE， EOD90COD90 1 2AOD， EOB90AOC90 1 2AOD， EODEOB； OE 在 AB 的下面，如图， 同 OE 在 AB 上面的方法得，EODEOB 4 【解答】解：测量可得半圆半径为 2cm，扇形半径为 4cm S半圆3.142226.28（cm2） ， S扇形3.1442412.56（cm2） ， S阴影12.566.286.28 （cm2） 5
26、 【解答】解： （1）COEDOEAOC907020， 故答案为：20 （2）OC 平分AOE，AOC70， COEAOC70， DOE90， CODDOECOE907020 （3）COEAOD20或COE20+AOD 理由如下： 当 OD 始终在AOC 的内部时，有AOD+COD70，COE+COD90， COEAOD907020， COEAOD20或COE20+AOD 6 【解答】解： （1）证明：点 O 在直线 AD 上， AOB+BOD180 即AOB+BOC+COD180 AOC+COD180 OC 平分BOD， BOCCOD AOC+BOC180 AOC 与BOC 互补 （2）如图
27、所示即为所求作的图形 （3）如图， EPQ 和FPQ 互余， 射线 PM 平分EPQ， 射线 PN 平分FPQ 锐角MPN 的度数是 45 EPQ 和FPQ 互余， 射线 PM 平分EPQ， 射线 PN 平分FPQ 若EPQ， PQ 平分FPF 则锐角MPN 的度数是|45| 故答案为：45或|45| 7 【解答】解： （1）小明解答过程中的“”为线段中点的定义； 故答案为：线段中点的定义； （2）我同意小芳的说法，将小明的解答补充如下： 如图： AB8，BC2， ACAB+BC8+210 M 是 AC 的中点， = 1 2 = 1 2 10 = 5 8 【解答】证明：AOB30，COB20（
28、已知） ， AOCAOB+COB50 OC 平分AOD（已知） ， AOCCOD50（角平分线定义 ） 故答案为：AOB；COB；50；COD；50 9 【解答】 （1）解：符合题意的图形有两个， 如图， ABC90，CBD30， ABDABCCBD60 BP 平分ABD， = 1 2 = 30 如图， ABC90，CBD30， ABDABC+CBD120 BP 平分ABD， = 1 2 = 60 综上，ABP 的度数为 30或 60 （2）由（1）可知： ABCa，CBD， ABP= + 2 或 2 10 【解答】解：O 是直线 AB 上的一点， （已知） BOC180AOC （平角定义）
29、AOC60， （已知） BOC120 （等量代换） OE 平分BOC， （已知） COE= 1 2 （角平分线定义） COE60 DOECODCOE，且COD90， DOE30 故答案为：平角定义；等量代换；角平分线定义；60；30 11 【解答】解：因为点 C 是线段 AB 的中点， 所以 ACBC， 因为 BC6cm， 所以 AC6cm， 因为点 D 是线段 AC 的中点， 所以 DC= 1 2AC 所以 DC3cm 所以 BDCD+BD9cm， 故答案为：ACBC，6，1 2AC，3，CD+BD，9 12 【解答】解： （1）补全图形，如图所示： 点 A、O、B 在同一条直线上， AOC
30、+BOC180（平角的定义） AOC：BOC8：1， BOC20，AOC160 COD2COB， COD40 AOD180COBCOD120 OE 平分AOD， EOD= 1 2AOD60（角平分线的定义） EOCEOD+DOC60+40100 （2）当射线 OD 在AOC 的内部时，EOC5； 当射线 OD 在AOC 的外部时，EOC3 答：COE 的度数为：5 或 3 13 【解答】解：因为 OE 平分AOC，OF 平分BOC 所以EOC= 1 2AOC，FOC= 1 2 =BOC 所以EOFEOCFOC = 1 2（AOCBOC） = 1 2AOB 45 故答案为：BOC、FOC、BOC
31、、AOB、45 14 【解答】解： （1）如图 1，当 C 在点 A 右侧时， AB8，AC2， BCABAC6， D 是线段 BC 的中点， = 1 2 = 3； 如图 2，当 C 在点 A 左侧时， AB8，AC2， BCAB+AC10， D 是线段 BC 的中点， = 1 2 = 5； 综上所述，CD3 或 5； （2）AB2DE，理由是： 如图 3，当 C 在点 A 右侧时， E 是 AC 的中点，D 是 BC 的中点， AC2EC，BC2CD， ABAC+BC2EC+2CD2ED； 如图 4，当 C 在点 A 左侧时， 同理可得：ABBCAC2CD2CE2（CDCE）2DE 15 【
32、解答】证明：O 是直线 AB 上一点 AOB180 COD 与COE 互余 COD+COE90 AOD+BOE90 OD 是AOC 的平分线 AODCOD（理由：角平分线的定义） BOECOE（理由：等式性质） AOE+BOE180 AOE+COE180 AOE 与COE 互补 故答案为：90；COD； 角平分线的定义；等式性质 16 【解答】解：如图所示， 17 【解答】解：根据题意 E 面和 F 面的数互为相反数， 3a+4+2a0， a3， 把 a3 代入 Ca22a+1， 解得：C2， A 面与 C 面表示的数互为相反数， A 面表示的数值是 2 18 【解答】解： （1）由已知得BO
33、C180AOC150， 又COD 是直角，OE 平分BOC， DOECOD 1 2BOC90 1 2 15015； （2）AOC2DOE； 理由：COD 是直角，OE 平分BOC， COEBOE90DOE， 则得AOC180BOC1802COE1802（90DOE） ， 所以得：AOC2DOE； （3）AOC3602DOE； 理由：OE 平分BOC， BOE2COE， 则得AOC180BOE1802COE1802（DOE90） ， 所以得：AOC3602DOE； 故答案为： （1）15； （3）AOC3602DOE 19 【解答】解： （1）OC 是AOB 的平分线（已知） ， AOC= 1
34、2AOB， AOB60， AOC30 （2）OEOC， EOC90， 如图 1， AOECOE+COA90+30120 如图 2， AOECOECOA903060 （3）AOE90+ 1 2 或AOE90 1 2 20 【解答】解： （1）点 O 为直线 AB 上一点， AOB180 BOC120， AOC60 OD 平分AOC， COD= 1 2AOC COD30 故答案为：180；60；30； （2）分情况讨论： 当 OE 在BOC 的内部时，COE+BOE120， COE：BOE4：1， 5BOE120， 即BOE24； OE 在BOC 的外部时，COE+BOE360120240， CO
35、E：BOE4：1， BOE240548， COE192（不合题意，舍去） ； OE 在BOC 外部时， BOE120340 故BOE 的度数为 24或 40 21 【解答】解：AC2BC，BC3 AC6， ABAC+BC9， 又D 为 AB 中点 BD= 1 2AB4.5， CDBDBC1.5 故答案为 6，9，D 为 AB 中点，AB，4.5，1.5 22 【解答】解： （1）AC8，CB6， ABAC+CB14 点 M、N 分别是 AC、BC 的中点， MC= 1 2AC，NC= 1 2BC（线段中点的定义） ， MN= 1 2（AC+BC）7； （2）理由如下：点 M、N 分别是 AC、
36、BC 的中点， MC= 1 2AC，NC= 1 2BC， MNMC+NC= 1 2AC+ 1 2BCb， ACa， BC2ba， 线段 BC 的长用含 a，b 的代数式可以表示为 2ba 故答案为：1 2， 1 2，线段中点的定义， 1 2（AC+BC） ，7，2ba 23 【解答】解： （1）补全图形，并猜想DAB+EBA 的度数等于 45； （2）证明：AD 平分CAB，BE 平分ABC， DAB= 1 2CAB， EBA= 1 2CBA （理由：角平分线的定义） CAB+ABC90， DAB+EBA= 1 2 （CAB+ABC）45 故答案为：45，1 2CAB，角平分线的定义， 1 2
37、，CAB，ABC，45 24 【解答】解：AOCAOB+BOC， 又AOB40，BOC60， AOC100 OD 平分AOC， AOD= 1 2AOC（角平分线定义） AOD50 BODAODAOB BOD10 故答案为：BOC，100，角平分线定义，AOB，10 25 【解答】解： （1）如图所示， （2）通过观察、测量你发现DOE90； （3）OD 平分AOC（已知） ， DOC= 1 2AOC（ 角平分线定义 ） ， OE 平分BOC（已知） ， EOC= 1 2BOC（角平分线定义 ） ， AOC+BOC180， DOEDOC+EOC= 1 2 （AOC+BOC）90 故答案为：90，
38、角平分线定义，角平分线定义，180，90 26 【解答】解： （1）O 是直线 AB 上一点， AOC+BOC180 AOC50， BOC130 OE 平分BOC（已知） ， COE= 1 2BOC（角平分线定义） COE65 COD90，DOECODCOE DOE25， 故答案为：角平分线定义，65，COD，COE，25； （2）DOE= 1 2AOC， 理由：O 是直线 AB 上一点， AOC+BOC180 BOC180AOC， OE 平分BOC（已知） ， COE= 1 2BOC（角平分线定义） ， COD90，DOECODCOE DOE90 1 2（180AOC）= 1 2AOC 故答
39、案为：DOE= 1 2AOC 27 【解答】解： （1）AOC+BOC180，AOC40， BOC140， OE 平分BOC， COE= 1 2BOC 70， COD90， DOECODCOE20； 故答案为：20； （2）AOC+BOC180，AOC160， BOC18016020； OE 平分BOC， COE= 1 2BOC10， COD90， DOE901080； 故答案为：80； （3） DOE= 1 2AOC= 2（0AOC180） ， DOE180 1 2AOC180 2（0DOE 180） 28 【解答】解： （1）正方体的左面 B 与右面 D 代表的代数式的值相等， x13x2
40、， 解得 x= 1 2； （2）正面字母 A 代表的代数式与对面 F 代表的代数式的值相等， kx+1x， （k1）x1， x 为整数， x，k1 为1 的因数， k11， k0 或 k2， 综上所述，整数 k 的值为 0 或 2 29 【解答】解： （1）如图所示： （2）根据测量可得，点 B 到直线 AC 的距离，大约是 1.5cm， 故答案为：1.5 30 【解答】解： （1）如图 2，AOB120，OC 平分AOB BOC= 1 2AOB60 COD20， BOD602040 故答案为：1 2；60；40； （2）如图 1，AOB120，OC 平分AOB BOC= 1 2AOB60 C
41、OD20， BOD60+2080 故答案为：80 31 【解答】解： （1）方法一： AC8，CB2， ABAC+CB10， 点 M 为线段 AB 的中点， = 1 2 = 5， CMBMCB523 或方法二： CMACAM853 （2）点 M 是线段 CD 的中点，理由如下： 方法一： BDAC8， 由（1）可知，DMDBMB853 DMMC3， 由图可知，点 M 是线段 CD 的中点 方法二： ACBD， ACDCBDDC， ADCB 点 M 为线段 AB 的中点， AMMB， AMADMBCB， DMMC 由图可知，点 M 是线段 CD 的中点 32 【解答】解：因为AOB90 所以BO
42、C+AOC90 因为COD90 所以AOD+AOC90 所以BOCAOD （同角的余角相等） 因为BOC20 所以AOD20 因为 OA 平分DOE 所以DOE2AOD40 （角平分线的定义） 所以COECODDOE50 故答案为：同角的余角相等，DOE，40，角平分线的定义，50 33 【解答】证明：O+OCA90，O+OBC90， OCAOBC （理由：同角的余角相等） CA 平分OCD ACDOCA （理由：角平分线的定义） ACDOBC （理由：等量代换） 故答案为：OBC，同角的余角相等，OCA，角平分线的定义，等量代换 34 【解答】证明：如图，因为 OE 是BOC 的平分线， 所以BOECOE（角平分线定义） 因为DOE90， 所以DOC+COE90， 且DOA+BOE180DOE90 所以DOC+COEDOA+BOE 所以DOCDOA 所以 OD 是AOC 的平分线 故答案为：角平分线定义；COE；90；COE；DOC；DOA
