1、第第 22 章二次函数解答题精选章二次函数解答题精选(2) 1 （2019 秋东城区期末）为迎接国庆节，某商店购进了一批成本为每件 30 元的纪念商品，经调查发现， 该商品每天的销售量 y（件）与销售单价 x（元）满足一次函数关系，其图象如图所示 （1）求该商品每天的销售量 y 与销售单价 x 的函数关系式； （2）若商店按不低于成本价，且不高于 60 元的单价销售，则销售单价定为多少元，才能使销售该商品 每天获得的利润 w（元）最大？最大利润是多少？ 2 （2019 秋东城区期末）二次函数 yax2+bx+c（a，b，c 是常数，a0）的自变量 x 与函数值 y 的部分对 应值如表： x 2
2、 1 0 1 2 y ax2+bx+c t m 2 2 n 根据以上列表，回答下列问题： （1）直接写出 c 的值和该二次函数图象的对称轴； （2）写出关于 x 的一元二次方程 ax2+bx+ct 的根； （3）若 m1，求此二次函数的解析式 3 （2019 秋铁西区期末）抛物线 yax2+bx+c 上部分点的横坐标 x，纵坐标 y 的对应值如下表： x 3 2 1 0 1 y 0 4 3 0 （1）把表格填写完整； （2）根据上表填空： 抛物线与 x 轴的交点坐标是 和 ； 在对称轴右侧，y 随 x 增大而 ； 当2x2 时，则 y 的取值范围是 （3）确定抛物线 yax2+bx+c 的解析
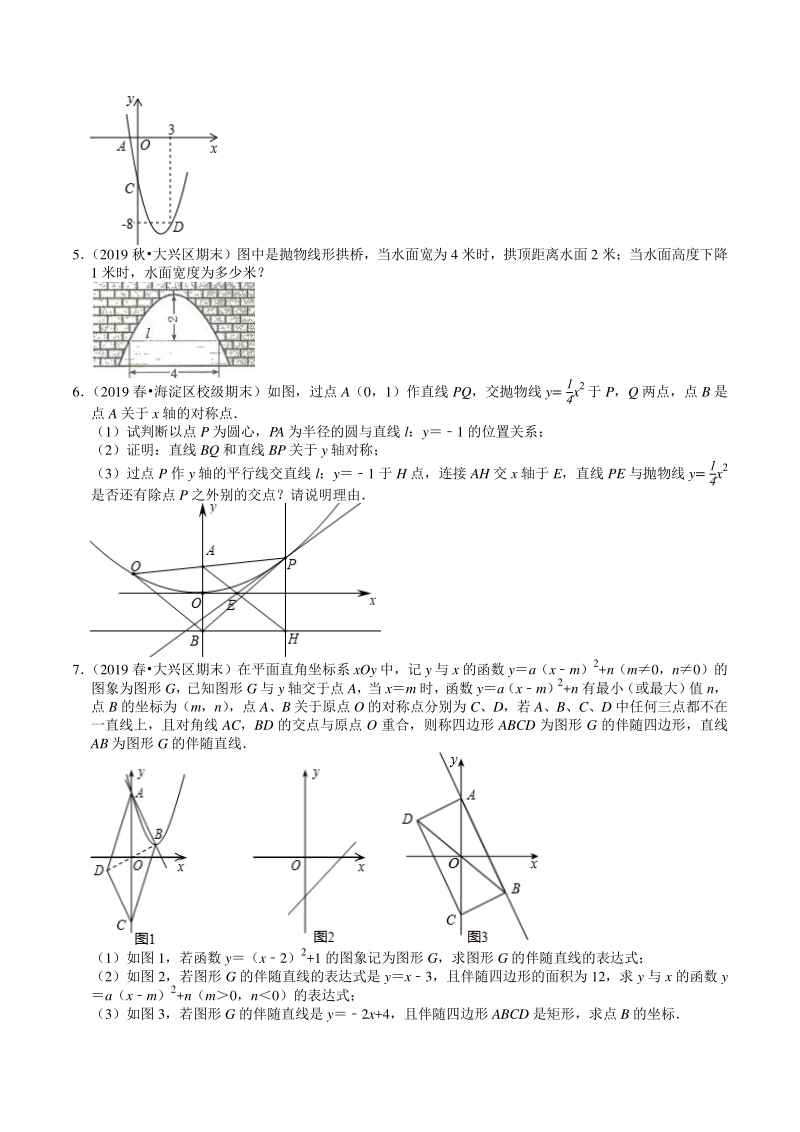
3、式； 4（2019 秋西湖区校级期末） 二次函数 yax2+bx+c 的部分图象如图所示， 其中图象与 x 轴交于点 A （1， 0） ，与 y 轴交于点 C（0，5） ，且经过点 D（3，8） （1）求此二次函数的解析式； （2）将此二次函数的解析式写成 ya（xh）2+k 的形式，并直接写出顶点坐标以及它与 x 轴的另一个 交点 B 的坐标 （3）利用以上信息解答下列问题：若关于 x 的一元二次方程 ax2+bx+ct0（t 为实数）在1x3 的范围内有解，则 t 的取值范围是 5 （2019 秋大兴区期末）图中是抛物线形拱桥，当水面宽为 4 米时，拱顶距离水面 2 米；当水面高度下降 1
4、 米时，水面宽度为多少米？ 6 （2019 春海淀区校级期末）如图，过点 A（0，1）作直线 PQ，交抛物线 y= 1 4x 2 于 P，Q 两点，点 B 是 点 A 关于 x 轴的对称点 （1）试判断以点 P 为圆心，PA 为半径的圆与直线 l：y1 的位置关系； （2）证明：直线 BQ 和直线 BP 关于 y 轴对称； （3）过点 P 作 y 轴的平行线交直线 l：y1 于 H 点，连接 AH 交 x 轴于 E，直线 PE 与抛物线 y= 1 4x 2 是否还有除点 P 之外别的交点？请说明理由 7 （2019 春大兴区期末）在平面直角坐标系 xOy 中，记 y 与 x 的函数 ya（xm
5、）2+n（m0，n0）的 图象为图形 G，已知图形 G 与 y 轴交于点 A，当 xm 时，函数 ya（xm） 2+n 有最小 （或最大） 值 n， 点 B 的坐标为（m，n） ，点 A、B 关于原点 O 的对称点分别为 C、D，若 A、B、C、D 中任何三点都不在 一直线上，且对角线 AC，BD 的交点与原点 O 重合，则称四边形 ABCD 为图形 G 的伴随四边形，直线 AB 为图形 G 的伴随直线 （1）如图 1，若函数 y（x2）2+1 的图象记为图形 G，求图形 G 的伴随直线的表达式； （2）如图 2，若图形 G 的伴随直线的表达式是 yx3，且伴随四边形的面积为 12，求 y 与
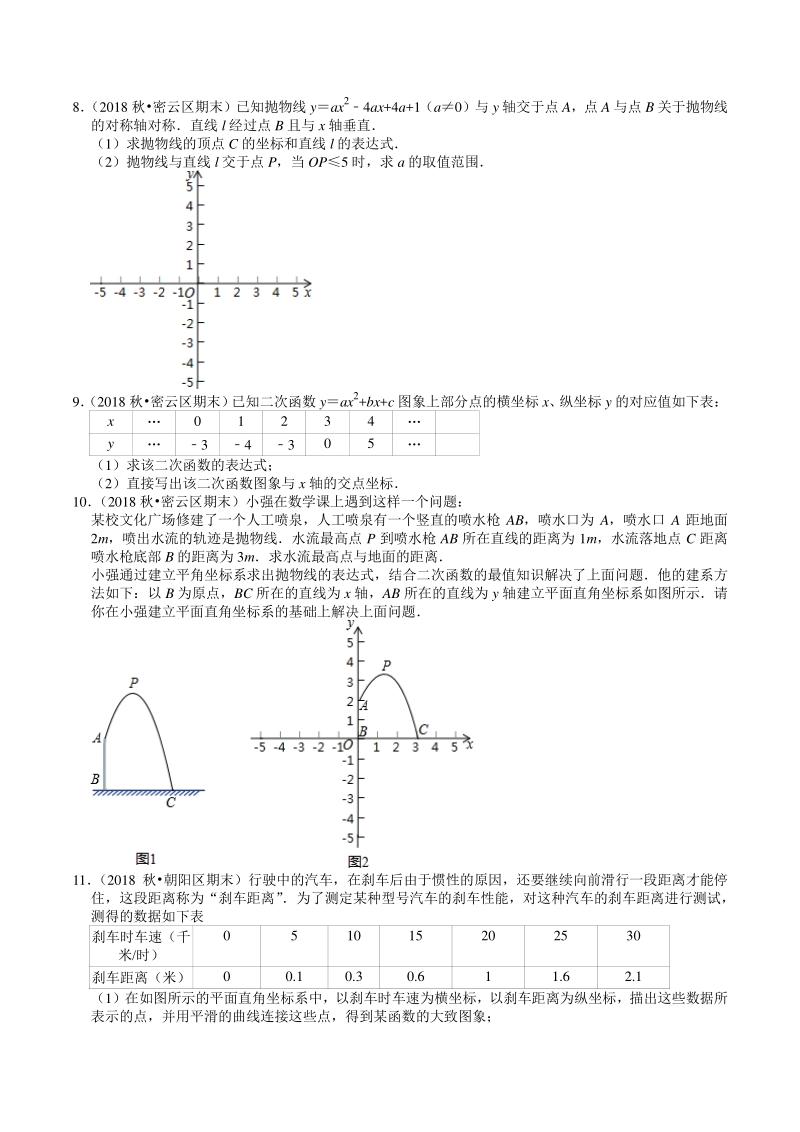
6、 x 的函数 y a（xm）2+n（m0，n0）的表达式； （3）如图 3，若图形 G 的伴随直线是 y2x+4，且伴随四边形 ABCD 是矩形，求点 B 的坐标 8 （2018 秋密云区期末）已知抛物线 yax24ax+4a+1（a0）与 y 轴交于点 A，点 A 与点 B 关于抛物线 的对称轴对称直线 l 经过点 B 且与 x 轴垂直 （1）求抛物线的顶点 C 的坐标和直线 l 的表达式 （2）抛物线与直线 l 交于点 P，当 OP5 时，求 a 的取值范围 9 （2018 秋密云区期末） 已知二次函数 yax2+bx+c 图象上部分点的横坐标 x、 纵坐标 y 的对应值如下表： x 0
7、1 2 3 4 y 3 4 3 0 5 （1）求该二次函数的表达式； （2）直接写出该二次函数图象与 x 轴的交点坐标 10 （2018 秋密云区期末）小强在数学课上遇到这样一个问题： 某校文化广场修建了一个人工喷泉，人工喷泉有一个竖直的喷水枪 AB，喷水口为 A，喷水口 A 距地面 2m，喷出水流的轨迹是抛物线水流最高点 P 到喷水枪 AB 所在直线的距离为 1m，水流落地点 C 距离 喷水枪底部 B 的距离为 3m求水流最高点与地面的距离 小强通过建立平角坐标系求出抛物线的表达式，结合二次函数的最值知识解决了上面问题他的建系方 法如下：以 B 为原点，BC 所在的直线为 x 轴，AB 所在
8、的直线为 y 轴建立平面直角坐标系如图所示请 你在小强建立平面直角坐标系的基础上解决上面问题 11 （2018 秋朝阳区期末）行驶中的汽车，在刹车后由于惯性的原因，还要继续向前滑行一段距离才能停 住，这段距离称为“刹车距离” 为了测定某种型号汽车的刹车性能，对这种汽车的刹车距离进行测试， 测得的数据如下表 刹车时车速（千 米/时） 0 5 10 15 20 25 30 刹车距离（米） 0 0.1 0.3 0.6 1 1.6 2.1 （1）在如图所示的平面直角坐标系中，以刹车时车速为横坐标，以刹车距离为纵坐标，描出这些数据所 表示的点，并用平滑的曲线连接这些点，得到某函数的大致图象； （2）测量
9、必然存在误差，通过观察图象估计函数的类型，求出一个大致满足这些数据的函数表达式； （3）一辆该型号汽车在高速公路上发生交通事故，现场测得刹车距离约为 40 米，已知这条高速公路限 速 100 千米/时，请根据你确定的函数表达式，通过计算判断在事故发生时，汽车是否超速行驶 12 （2018 秋朝阳区期末）在平面直角坐标系 xOy 中，抛物线 yax2+（12a）x2（a0）与 y 轴交于 点 C，当 a1 时，该抛物线与 x 轴的两个交点为 A，B（点 A 在点 B 左侧） （1）求点 A，B，C 的坐标； （2）若该抛物线与线段 AB 总有两个公共点，结合函数的图象，求 a 的取值范围 13
10、（2018 秋海淀区期末）在平面直角坐标系 xOy 中，已知抛物线 G：y4x28ax+4a24，A（1，0） ， N（n，0） （1）当 a1 时， 求抛物线 G 与 x 轴的交点坐标； 若抛物线 G 与线段 AN 只有一个交点，求 n 的取值范围； （2）若存在实数 a，使得抛物线 G 与线段 AN 有两个交点，结合图象，直接写出 n 的取值范围 14 （2018 秋石景山区期末）在平面直角坐标系 xOy 中，直线 ykx+b（k0）与抛物线 yax24ax+3a 的对称轴交于点 A（m，1） ，点 A 关于 x 轴的对称点恰为抛物线的顶点 （1）求抛物线的对称轴及 a 的值； （2）横、
11、纵坐标都是整数的点叫做整点记直线 ykx+b（k0）与抛物线围成的封闭区域（不含边界） 为 W 当 k1 时，直接写出区域 W 内的整点个数； 若区域 W 内恰有 3 个整点，结合函数图象，求 b 的取值范围 15 （2018 秋西城区期末）小明利用函数与不等式的关系，对形如（xx1） （xx2）（xxn）0 （n 为正整数）的不等式的解法进行了探究 （1）下面是小明的探究过程，请补充完整： 对于不等式 x30，观察函数 yx3 的图象可以得到如表格： x 的范围 x3 x3 y 的符号 + 由表格可知不等式 x30 的解集为 x3 对于不等式（x3） （x1）0，观察函数 y（x3） （x1
12、）的图象可以得到如表表格： x 的范围 x3 1x3 x1 y 的符号 + + 由表格可知不等式（x3） （x1）0 的解集为 对于不等式（x3） （x1） （x+1）0，请根据已描出的点画出函数 y（x3） （x1） （x+1）的图 象； 观察函数 y（x3） （x1） （x+1）的图象补全下面的表格： x 的范围 x3 1x3 1x1 x1 y 的符号 + 由表格可知不等式（x3） （x1） （x+1）0 的解集为 小明将上述探究过程总结如下：对于解形如（xx1） （xx2）（xxn）0（n 为正整数）的不等式， 先将 x1，x2，xn按从大到小的顺序排列，再划分 x 的范围，然后通过列表
13、格的办法，可以发现表格中 y 的符号呈现一定的规律，利用这个规律可以求这样的不等式的解集 （2）请你参考小明的方法，解决下列问题： 不等式（x6） （x4） （x2） （x+2）0 的解集为 不等式（x9） （x8） （x7）20 的解集为 16 （2018 秋通州区期末）在平面直角坐标系 xOy 中，抛物线 yax24ax+m（a0）与 x 轴的交点为 A、 B， （点 A 在点 B 的左侧） ，且 AB2 （1）求抛物线的对称轴及 m 的值（用含字母 a 的代数式表示） ； （2）若抛物线 yax24ax+m（a0）与 y 轴的交点在（0，1）和（0，0）之间，求 a 的取值范围； （3）
14、横、纵坐标都是整数的点叫做整点若抛物线在点 A，B 之间的部分与线段 AB 所围成的区域内（包 括边界）恰有 5 个整点，结合函数的图象，直接写出 a 的取值范围 17 （2018 秋平谷区期末）在平面直角坐标系 xOy 中，抛物线 yax2+bx+3（a0）经过（1，0） ，且与 y 轴交于点 C （1）直接写出点 C 的坐标 ； （2）求 a，b 的数量关系； （3）点 D（t，3）是抛物线 yax2+bx+3 上一点（点 D 不与点 C 重合） 当 t3 时，求抛物线的表达式； 当 3CD4 时，求 a 的取值范围 18 （2018 秋东城区期末）在平面直角坐标系 xOy 中，抛物线的表
15、达式为 y2x2+4mx2m2+2m，线段 AB 的两个端点分别为 A（1，2） ，B（3，2） （1）若抛物线经过原点，求出 m 的值； （2）求抛物线顶点 C 的坐标（用含有 m 的代数式表示） ； （3）若抛物线与线段 AB 恰有一个公共点，结合函数图象，求出 m 的取值范围 19 （2018 秋石景山区期末）小明用篱笆围出一块周长为 12m 的矩形空地做生物试验，已知矩形的一边长 为 x（单位：m） ，面积为 y（单位：m2） （1）求 y 与 x 的函数表达式，并写出自变量 x 的取值范围； （2）当 x 为何值时，矩形的面积最大？并求出此最大面积 20 （2018 秋丰台区期末）小
16、哲的姑妈经营一家花店，随着越来越多的人喜爱“多肉植物” ，姑妈也打算销 售“多肉植物” 小哲帮助姑妈针对某种“多肉植物”做了市场调查后，绘制了以下两张图表： （1）如果在三月份出售这种植物，单株获利 元； （2）请你运用所学知识，帮助姑妈求出在哪个月销售这种多肉植物，单株获利最大？（提示：单株获利 单株售价单株成本） 21 （2018 秋东城区期末）已知二次函数 yax2+bx+c（a0）自变量 x 的部分取值及对应的函数值 y 如表 所示： x 2 1 0 1 2 y 3 2 3 6 11 （1）写出此二次函数图象的对称轴； （2）求此二次函数的表达式 22 （2018 秋门头沟区期末）已知
17、二次函数 yx24x+3 （1）用配方法将其化为 ya（xh）2+k 的形式； （2）在所给的平面直角坐标系 xOy 中，画出它的图象 23 （2018 秋顺义区期末）某商店购进一批单价为 8 元的商品，如果按每件 10 元出售，那么每天可销售 100 件，为提高利润，欲对该商品进行涨价销售经调查发现，这种商品的销售单价每提高 1 元，其销 售量相应减少 10 件，将销售价定为多少时，才能使每天所获销售利润最大？最大利润是多少？ 24 （2018 秋门头沟区期末）如果抛物线 yx2+2x+2k4 与 x 轴有两个不同的公共点 （1）求 k 的取值范围； （2）如果 k 为正整数，且该抛物线与
18、x 轴的公共点的横坐标都是整数，求 k 的值 25 （2018 秋西城区期末）已知一个二次函数图象上部分点的横坐标 x 与纵坐标 y 的对应值如表所示： x 3 2 1 0 1 y 0 3 4 3 0 （1）求这个二次函数的表达式； （2）在给定的平面直角坐标系中画出这个二次函数的图象； （3）当4x2 时，直接写出 y 的取值范围 26 （2018 秋西城区期末）一名同学推铅球，铅球出手后行进过程中离地面的高度 y（单位：m）与水平距 离 x（单位：m）近似满足函数关系 y= 1 12x 2+2 3x+c，其图象如图所示已知铅球落地时的水平距离为 10m （1）求铅球出手时离地面的高度； （
19、2）在铅球行进过程中，当它离地面的高度为11 12m 时，求此时铅球的水平距离 27 （2018 秋西城区期末）如图，直线 l：y2x+m 与 x 轴交于点 A（2，0） ，抛物线 C1：yx2+4x+3 与 x 轴的一个交点为 B（点 B 在点 A 的左侧） ，过点 B 作 BD 垂直 x 轴交直线 l 于点 D （1）求 m 的值和点 B 的坐标； （2）将ABD 绕点 A 顺时针旋转 90，点 B，D 的对应点分别为点 E，F 点 F 的坐标为 ； 将抛物线 C1向右平移使它经过点 F，此时得到的抛物线记为 C2，直接写出抛物线 C2的表达式 28 （2018 秋西城区期末）在平面直角坐
20、标系 xOy 中，已知抛物线 yax24ax+3a （1）求抛物线的对称轴； （2）当 a0 时，设抛物线与 x 轴交于 A，B 两点（点 A 在点 B 左侧） ，顶点为 C，若ABC 为等边三角 形，求 a 的值； （3）过 T （0，t） （其中1t2）且垂直 y 轴的直线 l 与抛物线交于 M，N 两点若对于满足条件的 任意 t 值，线段 MN 的长都不小于 1，结合函数图象，直接写出 a 的取值范围 29 （2018 秋怀柔区期末）已知二次函数 yx22x3 （1）将 yx22x3 化成 ya（xh）2+k 的形式； （2）求该二次函数图象的顶点坐标 30 （2018 秋平谷区期末）二
21、次函数 yax22ax3（a0）的图象经过点 A （1）求二次函数的对称轴； （2）当 A（1，0）时， 求此时二次函数的表达式； 把 yax22ax3 化为 ya（xh）2+k 的形式，并写出顶点坐标； 画出函数的图象 31 （2018 秋昌平区期末）在平面直角坐标系 xOy 中，抛物线 ymx24mx+4m2 的顶点为 M （1）顶点 M 的坐标为 （2）横、纵坐标都是整数的点叫做整点若 MNy 轴且 MN2 点 N 的坐标为 ； 过点 N 作 y 轴的垂线 l，若直线 l 与抛物线交于 P、Q 两点，该抛物线在 P、Q 之间的部分与线段 PQ 所围成的区域（包括边界）恰有七个整点，结合函
22、数图象，求 m 的取值范围 32 （2018 秋北京期末）如图是抛物线型拱桥，当拱顶离水面 8m 时，水面宽 AB 为 12m当水面上升 6m 时达到警戒水位，此时拱桥内的水面宽度是多少 m？ 下面给出了解决这个问题的两种方法，请补充完整： 方法一：如图 1，以点 A 为原点，AB 所在直线为 x 轴，建立平面直角坐标系 xOy， 此时点 B 的坐标为（ ， ） ，抛物线的顶点坐标为（ ， ） ， 可求这条抛物线所表示的二次函数的解析式为 当 y6 时，求出此时自变量 x 的取值，即可解决这个问题 方法二：如图 2，以抛物线顶点为原点，对称轴为 y 轴，建立平面直角坐标系 xOy， 这时这条抛
23、物线所表示的二次函数的解析式为 当 y 时，求出此时自变量 x 的取值为 ，即可解决这个问题 第第 22 章二次函数解答题精选章二次函数解答题精选(2) 参考答案与试题解析参考答案与试题解析 一解答题（共一解答题（共 32 小题）小题） 1 【解答】解： （1）设 y 与 x 的函数关系式为 ykx+b（k0） ， 将（30，100） 、 （45，70）代入，得 30 + = 100 45 + = 70 解得 = 2 = 160 故函数关系式为 y2x+160 答：该商品每天的销售量 y 与销售单价 x 的函数关系式为 y2x+160 （2）由题意，得 w（x30） （2x+160） 2（x5
24、5）2+1250 20， 故当 x55 时，w 随 x 的增大而增大， 又 30 x60， 当 x55 时，w 取得最大值，最大值为 1250 元 答：销售单价定为 55 元，才能使销售该商品每天获得的利润 w（元）最大，最大利润是 1250 元 2 【解答】解： （1）根据图表可知： 二次函数 yax2+bx+c 的图象过点（0，2） ， （1，2） ， 对称轴为直线 x= 0+1 2 = 1 2，c2； （2）根据二次函数的对称性可知： （2，t）关于对称轴 x= 1 2的对称点为（3，t） ， 即2 和 3 是关于 x 的方程 ax2+bx+ct 的两个根； （3）若 m1，则抛物线经过
25、点（1，1） ， （0，2） ， （1，2） ， 代入 yax2+bx+c 得 + = 1 = 2 + + = 2 ， 解得 = 1 2 = 1 2 = 2 ， 此二次函数的解析式为 y= 1 2x 21 2x2 3 【解答】解： （1）x3，y0；x1，y0， 抛物线的对称轴为直线 x1， x0 和 x2 时，y3； （2）抛物线与 x 轴的交点坐标是（3，0）和（1，0） ； 设抛物线解析式为 ya（x+3） （x1） ， 把（0，3）代入得 33a，解得 a1， 抛物线解析式为 y（x+3） （x1） ，即 yx22x+3， 抛物线的顶点坐标为（1，4） ，抛物线开口向下， 在对称轴右侧
26、，y 随 x 增大而减小； 当 x2 时，y3；当 x2 时，y44+35， 当2x2 时，则 y 的取值范围是5y4 （3）由（2）得抛物线解析式为 yx22x+3， 故答案为（3，0） 、 （1，0） ；减小；5y4 4 【解答】解： （1）根据题意得， + = 0 = 5 9 + 3 + = 8 ， 分别代入、得， ab5， 3a+b1， +得，4a4， 解得 a1， 把 a1 代入得，1b5， 解得 b4， 方程组的解是 = 1 = 4 = 5 ， 此二次函数的解析式为 yx24x5； （2）yx24x5x24x+445（x2）29， 二次函数的解析式为 y（x2）29， 顶点坐标为（
27、2，9） ， 对称轴为 x2， 设另一点坐标为 B（a，0） ， 则1+a22， 解得 a5， 点 B 的坐标是 B（5，0） ； （3）由（1）可知二次函数解析式为 yx24x5， 即 y（x2）29， x1 时，y990， x3 时，y198， 关于 x 的一元二次方程 ax2+bx+ct0（t 为实数）在1x3 的范围内有解相当于 yax2+bx+c 与 直线 yt 的交点的横坐标， 当9t0 时，在1x3 的范围内有解 故答案为：9t0 5 【解答】解：建立平面直角坐标系如图： 则抛物线顶点 C 坐标为 （0， 2） ， 设抛物线解析式 yax2+2， 将 A 点坐标 （2， 0） 代
28、入， 可得： 04a+2， 解得：a0.5， 故抛物线解析式为 y0.5x2+2， 当水面下降 1 米，通过抛物线在图上的观察可转化为： 当 y1 时，对应的抛物线上两点之间的距离，也就是直线 y1 与抛物线相交的两点之间的距离， 将 y1 代入抛物线解析式得出：10.5x2+2， 解得：x6， 所以水面宽度为 26米 6 【解答】解： （1）以点 P 为圆心，PA 为半径的圆与直线 l：y1 的位置关系为相切 设点 P （m， 1 4m 2） ， 点 P 到直线 l： y1 的距离为 d=1 4 2+1， 则 PA=( 0)2+ (1 4 2 1)2= 1 4 2+1， d= 1 4m 2（
29、1）=1 4 2 +1， PAd 以点 P 为圆心，PA 为半径的圆与直线 l：y1 相切； （2）如图，过点 P 作 PH直线 l 于 H，作 PAy 轴于 M，过点 Q 作 QGl 于 G，QNy 轴于 N， 则：QGBQNAQNBGBNHBMPMAPHB90 四边形 BGQN、BHPM 均为矩形， BNQG，BMPH 由（1）知：PAPH，QAQG QABN，PABM PAMQAN PAMQAN = = BMPBNQ90 BMPBNQ PBMQBN 直线 BQ 和直线 BP 关于 y 轴对称； （3）除点 P 之外无别的交点 P（m，1 4 2） ，H（m，1） ，A（0，1） 设直线
30、AH 解析式为 ykx+b，则 + = 1 = 1 ，解得 = 2 = 1 直线 AH 解析式为 y= 2 x+1，令 y0，得 x= 2， E（ 2 ，0） 设直线 PE 解析式为 ykx+b，则 + = 1 4 2 2 + = 0 ，解得 = 1 2 = 1 4 2 直线 PE 解析式为 y= 1 2 x 1 4 2， 联立方程组 = 1 2 1 4 2 = 1 4 2 ，得1 4 2= 1 2 x 1 4 2， x22mx+m20 （2m）24m20 直线 PE 与抛物线 y= 1 4x 2 有且只有一个交点，即除点 P 之外无别的交点 7 【解答】解： （1）针对函数 y（x2）2+1
31、， 当 x2 时，此函数有最小值 1， B（2，1） ， 当 x0 时，y22+15， A（0，5） ， 设所求伴随直线的表达式为 ykx+b（k0） 则1 = 2 + ， 5 = . 解，得 = 2， = 5. 所以函数 y（x2）2+1 的伴随直线的表达式是 y2x+5； （2）如图 2，作 BEAC 于点 E， 由题意知，OCOA，OBOD， 四边形 ABCD 是平行四边形 A（0，3） ，C（0，3） AC6 平行四边形 ABCD 的面积为 12， SABC6 即= 1 2 = 6， BE2； m0，即顶点 B 在 y 轴的右侧，且在直线 yx3 上， B（2，1） 又图形 G 经过点
32、 A（0，3） ， = 1 2， = 1 2( 2) 2 1； （3）如图 3，作 BFx 轴于点 E， 由已知得：A（0，4） ，C（0，4） ， B（m，n）在直线 y2x+4 上， n2m+4，即点 B 的坐标为（m，2m+4） ， 矩形 ABCD， OCOB4， OC2OB2， 在 RtOEB 中，42m2+（2m+4）2， 5m216m0， m10（不合题意，舍去） ，2= 16 5 ， = 12 5 ， 点 B 的坐标为(16 5 ， 12 5 ) 8 【解答】解： （1）由 yax24ax+4a+1 得， yax24ax+4a+1a（x2）2+1， 抛物线的顶点 C 的坐标（2，
33、1） ， A（0，4a+1） ，点 A 与点 B 关于抛物线的对称轴对称， B（4，4a+1） ， 直线 l 经过点 B 且与 x 轴垂直， 直线 l 的表达式：x4； （2）设直线 l 与 x 轴交于点 Q，连接 OP OP5 时，OQ4， PQ3 当 OP5 时，PQ3 如图 1，a0 时，二次函数开口向上，点 A 位于 y 轴正半轴 4a+13， a 1 2， a 的取值范围为：0 1 2； 如图 2，a0 时，二次函数开口向下，点 A 位于 y 轴负半轴 （4a+1）3， a1， a 的取值范围为：1a0 综上，a 的取值范围为：1a 1 2，且 a0 9 【解答】解： （1）抛物线经
34、过点（0，3） ， （2，3） ， （1，4） ， 抛物线的对称轴为直线 x1，顶点坐标为（1，4） ， 设抛物线解析式为 ya（x1）24， 把（0，3）代入得 a（01）243，解得 a1， 抛物线解析式为 y（x1）24； （2）抛物线与 x 轴的一个交点坐标为（3，0） ， 而抛物线的对称轴为直线 x1， 抛物线与 x 轴的另一个交点坐标为（1，0） ， 即该二次函数图象与 x 轴的交点坐标为（1，0） ， （3，0） 10 【解答】解：由已知可得：A（0，2） ，B（3，0） ，抛物线对称轴为直线 x1， 设抛物线表达式为：yax2+bx+c， 则 = 2 9 + 3 + = 0 2
35、 = 1 ， 解得： = 2 3 = 4 3 = 2 ， 抛物线的表达式为：y= 2 3x 2+4 3x+2= 2 3（x1） 2+8 3， 当 x1 时，y 有最大值为：8 3， 水流到底面的最高距离为8 3m 11 【解答】解： （1）如图所示： （2）该图象可能为抛物线，猜想该函数为二次函数， 图象经过原点， 设二次函数的表达式为：yax2+bx（x0） ， 选取（20，1）和（10，0.3）代入表达式，得：400 + 20 = 1 100 + 10 = 0.3， 解得： = 1 500 = 1 100 ， 二次函数的表达式为：y= 1 500 x 2+1 100 x（x0） ， （3）
36、当 x100 时，y2140， 汽车已超速行驶 12 【解答】解： （1）当 a1 时，抛物线为 yx2x2， 点 C 的坐标为（0，2） ， 令，x2x20，解得 x11，x22， A 在点 B 左侧， A（1，0） ，B（2，0） ； （2）当 x0 时，yax2+（12a）x22；当 x2 时，yax2+（12a）x20， 所以抛物线 yax2+（12a）x2（a0）必过点 C 点和 B 点； 当 a0，当 x1 时，y0 时，抛物线与线段 AB 总有两个公共点，即 a1+2a20，解得 a1； 当 a0 时，当顶点为 B 点时，（12a）24a （2）0，解得 a= 1 2，则 a 1
37、 2时抛物线与 线段 AB 总有两个公共点， 综上所述，a 的取值范围为 a1 或 a 1 2 13 【解答】解： （1）把 a1 代入二次函数表达式得：y4x28x， 令 y0，即 4x28x0，解得：x0 或 2， 即抛物线 G 与 x 轴的交点坐标为： （2，0） 、 （0，0） ； 抛物线 G 与线段 AN 只有一个交点， 则 x1 时，y0（已经成立） ，xn 时，y0，且 n1， 4n28n0，解得：0n2， 故：0n2； （2）由知，抛物线 G 与线段 AN 有两个交点， 则 x1 时，y0，xn 时，y0， 即：4 + 8 + 4 2 4 0 2 2 + 2 1 0，解得： 0
38、或 2 1或 + 1， 即：n 的取值范围为：n3 或 n1 14 【解答】解： （1）变形得：ya（x24x）+3aa（x2）2a， 对称轴为 x2， 点 A 的坐标为（2，1）可得抛物线顶点为（2，1） ， 把点 A 坐标代入抛物线可得：a1 （2）当 k1 时，yx+b，把 A（2，1）代入得12+b， 解得：b3， yx3， 如图 1， 区域 W 内的整点个数为 2 个，分别为（2，0）与（1，1） 如图 2， i若 k0， 当直线过（1，2） ， （2，1）时，b3 当直线过（0，4） ， （2，1）时，b4 4b3， ii若 k0，由对称性可得：1b2 b 的取值范围是：4b3 或
39、 1b2 15 【解答】解： （1）由表格可知不等式（x3） （x1）0 的解集为 x3 或 x1， 故答案为：x3 或 x1； 图象如右图所示， 当1x1 时， （x3） （x1） （x+1）0，当 x1 时， （x3） （x1） （x+1）0， 由表格可知不等式（x3） （x1） （x+1）0 的解集为 x3 或1x1， 故答案为：+，x3 或1x1； （2）不等式（x6） （x4） （x2） （x+2）0 的解集为 x6 或 2x4 或 x2， 故答案为：x6 或 2x4 或 x2； 不等式（x9） （x8） （x7）20 的解集为 x9 或 x8 且 x7， 故答案为：x9 或 x8
40、且 x7 16 【解答】解： （1）由抛物线 yax24ax+m（a0）可知：对称轴为直线 x= 4 2 =2， AB2，点 A 在点 B 的左侧， A（1，0） ，B（3，0） ， 把 A（1，0）代入 yax24ax+m（a0）中，得 a4a+m0， m3a； （2）抛物线 yax24ax+m（a0）与 y 轴的交点在（0，1）和（0，0）之间， a0， 当抛物线经过点（0，1）时，可得 a= 1 3， a 的取值范围是 1 3a0； （3）yax24ax+ma（x2）24a+m， 顶点（2，4a+m） ， 线段 AB 上有三个整点（1，0） ， （2，0） ， （3，0） ， 当 a0
41、时，由题意得：34a+m2， m3a， 34a+3a2， 2a3， 当 a0 时，由题意得：24a+m3， m3a， 24a+3a3， 3a2 综上，a 的取值范围：2a3 或3a2 17 【解答】解： （1）由题意得：点 C 的坐标（0，3） ； 故答案为： （0，3） ； （2）把（1，0）代入抛物线 yax2+bx+3 中， 得：a+b+30； （3）把（3，3）和（1，0）代入抛物线 yax2+bx+3 中， 得9 + 3 + 3 = 3 + + 3 = 0 ，解得： = 3 2 = 9 2 ， 抛物线的表达式为：y= 3 2x 29 2x+3； 抛物线经过 C（0，3）和 D（t，3
42、）两点， 对称轴是：x= 1 2CD，CDx 轴， 抛物线 yax2+bx+3（a0）经过（1，0） ， 分两种情况： 当 a0 时， 3CD4， 3 2 2 2， 由（2）知：ba3， 3 2 +3 2 2， 1a 3 2； 当 a0 时， 3CD4， 2 2 3 2， 由（2）知：ba3， 2 +3 2 3 2， 0.75a0.6， 综上，a 的取值范围是 1a 3 2或0.75a0.6 18 【解答】解： （1）抛物线 y2x2+4mx2m2+2m 经过原点， 2m2+2m0， 解得 m10，m21； （2）y2x2+4mx2m2+2m2（x22mx+m2）+2m2（xm）2+2m， 顶
43、点 C 的坐标为（m，2m） ； （3）由顶点 C 的坐标可知，抛物线的顶点 C 在直线 y2x 上移动 当抛物线过点 A 时，m2 或 1； 当抛物线过点 B 时，m2 或 5 所以 m2 时，抛物线与线段 AB 有两个公共点，不符合题意 结合函数的图象可知，m 的取值范围为 1m5 且 m2 19 【解答】解： （1）由题意得：yx（6x）x2+6x， 0 6 0， 自变量的取值范围为：0 x6； （2）变形得：y（x3）2+9， 当 x3 时，函数 y 有最大值 又0 x6， 当 x3 时，函数 y 的最大值为 9， 答：当 x 为 3m 时，矩形的面积最大，此最大面积为 9m2 20
44、【解答】解： （1）从左图看，3 月份售价为 5 元，从右图看，3 月份的成本为 4 元， 则每株获利为 541（元） ， 故：答案为 1； （2）设直线的表达式为：y1kx+b（k0） ， 把点（3，5） 、 （6，3）代入上式得： 5 = 3 + 3 = 6 + ，解得： = 2 3 = 7 ， 直线的表达式为：y1= 2 3x+7； 设：抛物线的表达式为：y2a（xm）2+n， 顶点为（6，1） ，则函数表达式为：y2a（x6）2+1， 把点（3，4）代入上式得： 4a（36）2+1，解得：a= 1 3， 则抛物线的表达式为：y2= 1 3（x6） 2+1， y1y2= 2 3x+7 1
45、 3（x6） 21= 1 3x 2+10 3 x6， 1 30， x5 时，函数取得最大值， 故：5 月销售这种多肉植物，单株获利最大 21 【解答】解： （1）当 x2 时，y3；当 x0 时，y3， 二次函数图象的对称轴为直线 x= 2+0 2 ，即 x1 （2）将（1，2） ， （0，3） ， （1，6）代入 yax2+bx+c，得： + = 2 = 3 + + = 6 ， 解得： = 1 = 2 = 3 ， 此二次函数的表达式为 yx2+2x+3 22 【解答】解： （1）yx24x+3 x24x+2222+3（x2）21； （2） ）y（x2）21， 顶点坐标为（2，1） ，对称轴方
46、程为 x2 函数二次函数 yx24x+3 的开口向上，顶点坐标为（2，1） ，与 x 轴的交点为（3，0） ， （1，0） ， 其图象为： 23 【解答】解：设销售单价定为 x 元（x10） ，每天所获利润为 y 元， 则 y10010（x10） （x8） 10 x2+280 x1600 10（x14）2+360 所以将销售定价定为 14 元时，每天所获销售利润最大，且最大利润是 360 元 24 【解答】解： （1）根据题意得224（2k4）0， 解得 k 5 2； （2）k 5 2， 正整数 k 的值为 1，2， 当 k1 时，抛物线解析式为 yx2+2x2，当 y0 时，x2+2x20，
47、解得 x11+3，x213， 该抛物线与 x 轴的公共点的横坐标不是整数； 当 k2 时，抛物线解析式为 yx2+2x，当 y0 时，x2+2x0，解得 x10，x22，该抛物线与 x 轴的 公共点的横坐标为 0 和2， k 的值为 2 25 【解答】解： （1）由题意可得二次函数的顶点坐标为（1，4） ， 设二次函数的解析式为：ya（x+1）24， 把点（0，3）代入 ya（x+1）24，得 a1， 故抛物线解析式为 y（x+1）24，即 yx2+2x3； （2）如图所示： （3）y（x+1）24， 当 x4 时，y（4+1）245， 当 x2 时，y3， 又对称轴为 x1， 当4x2 时，
48、y 的取值范围是3y5 26 【解答】解： （1）根据题意，将（10，0）代入 y= 1 12x 2+2 3x+c，得： 1 12 102+ 2 3 10+c0， 解得 c= 5 3， 即铅球出手时离地面的高度5 3m； （2）将 y= 11 12代入 1 12x 2+2 3x+ 5 3 = 11 12， 整理，得：x28x90， 解得：x19，x21（舍） ， 此时铅球的水平距离为 9m 27 【解答】解： （1）将 A（2，0）代入 y2x+m，得：02（2）+m， 解得：m4 当 y0 时，有 x2+4x+30， 解得：x13，x21， 又点 B 在点 A 的左侧， 点 B 的坐标为（3，0） （2）当 x3 时，y2x42， 点 D 的坐标为（3，2） ， BD2，AB1 依照题意画出图形，则 EFBD2，OFAEAB1， 又点 A 的坐标为（2，0） ， 点 F 在 y 轴正半轴上， 点 F 的坐标为（0，1） yx2+4x+3（
