1、第第 22 章二次函数选择题精选章二次函数选择题精选 1 （2020 春海淀区校级期末）二次函数 yx2+px+q，当 0 x1 时，设此函数最大值为 8，最小值为 t，w st， （s 为常数）则 w 的值（ ） A与 p、q 的值都有关 B与 p 无关，但与 q 有关 C与 p、q 的值都无关 D与 p 有关，但与 q 无关 2 （2020 春海淀区校级期末）抛物线 y4x2向上平移 1 个单位长度得到的抛物线的解析式为（ ） Ay4x21 By4x2+1 Cy4（x+1）2 Dy4（x1）2 3 （2020 春海淀区校级期末）将抛物线 y（x3） （x5）先绕原点 O 旋转 180，再向
2、右平移 2 个单位 长度，所得抛物线的解析式为（ ） Ayx24x3 Byx212x35 Cyx2+12x+35 Dyx2+4x+3 4 （2019 秋通州区期末）如图，在平面直角坐标系 xOy 中，点 A（2，2） ，B（0，3） ，C（3，3） ，D （4，2） y 是关于 x 的二次函数，抛物线 y1经过点 A，B，C抛物线 y2经过点 B，C，D，抛物线 y3 经过点 A，B，D，抛物线 y4经过点 A，C，D，则下列判断其中正确的是（ ） 四条抛物线的开口方向均向下； 当 x0 时，四条抛物线表达式中的 y 均随 x 的增大而增大； 抛物线 y1的顶点在抛物线 y2顶点的上方； 抛物
3、线 y4与 y 轴交点在点 B 的上方 A B C D 5 （2019 秋大兴区期末）抛物线 y（x1）24 的顶点坐标为（ ） A （4，1） B （1，4） C （1，4） D （1，4） 6 （2019 秋大兴区期末）将二次函数 y2x2的图象向右平移 2 个单位，再向下平移 3 个单位，得到的函 数图象的表达式是（ ） Ay2（x+2）2+3 By2（x+2）23 Cy2（x2）23 Dy2（x2）2+3 7 （2019 秋石景山区期末）已知抛物线 yax2+bx+c（a0）上部分点的横坐标 x 与纵坐标 y 的对应值如 下表： x 2 1 0 1 2 3 y 4 0 2 2 0 4
4、下列结论： 抛物线开口向下； 当 x1 时，y 随 x 的增大而减小； 抛物线的对称轴是直线 x= 1 2； 函数 yax2+bx+c（a0）的最大值为 2 其中所有正确的结论为（ ） A B C D 8 （2019 秋平谷区期末）二次函数 ykx2+2x+1 的部分图象如图所示，则 k 的取值范围是（ ） Ak1 Bk1 Ck1 D0k1 9 （2019 秋北京期末）小悦乘座中国最高的摩天轮“南昌之星” ，从最低点开始旋转一圈，她离地面的高 度 y（米）与旋转时间 x（分）之间的关系可以近似地用二次函数来刻画经测试得出部分数据如表根 据函数模型和数据，可推断出南昌之星旋转一圈的时间大约是（
5、） x（分） 13.5 14.7 16.0 y（米） 156.25 159.85 158.33 A32 分 B30 分 C15 分 D13 分 10 （2019 秋顺义区期末）抛物线 yax2+bx+c 经过点（1，0） ，且对称轴为直线 x1，其部分图象如图 所示对于此抛物线有如下四个结论：abc0；2a+b0；9a3b+c0；若 mn0，则 xm 1 时的函数值小于 xn1 时的函数值其中正确结论的序号是（ ） A B C D 11 （2019 秋顺义区期末）关于下列二次函数图象之间的变换，叙述错误的是（ ） A将 y2x2+1 的图象向下平移 3 个单位得到 y2x22 的图象 B将 y
6、2（x1）2的图象向左平移 3 个单位得到 y2（x+2）2的图象 C将 y2x2的图象沿 x 轴翻折得到 y2x2的图象 D将 y2（x1）2+1 的图象沿 y 轴翻折得到 y2（x+1）21 的图象 12 （2019 秋西城区期末）下列关于抛物线 yx2+bx2 的说法正确的是（ ） A抛物线的开口方向向下 B抛物线与 y 轴交点的坐标为（0，2） C当 b0 时，抛物线的对称轴在 y 轴右侧 D对于任意的实数 b，抛物线与 x 轴总有两个公共点 13 （2019 秋门头沟区期末）将抛物线 y2x2先沿 x 轴向右平移 2 个单位长度，再向上平移 3 个单位长度 后得到新的抛物线，那么新抛
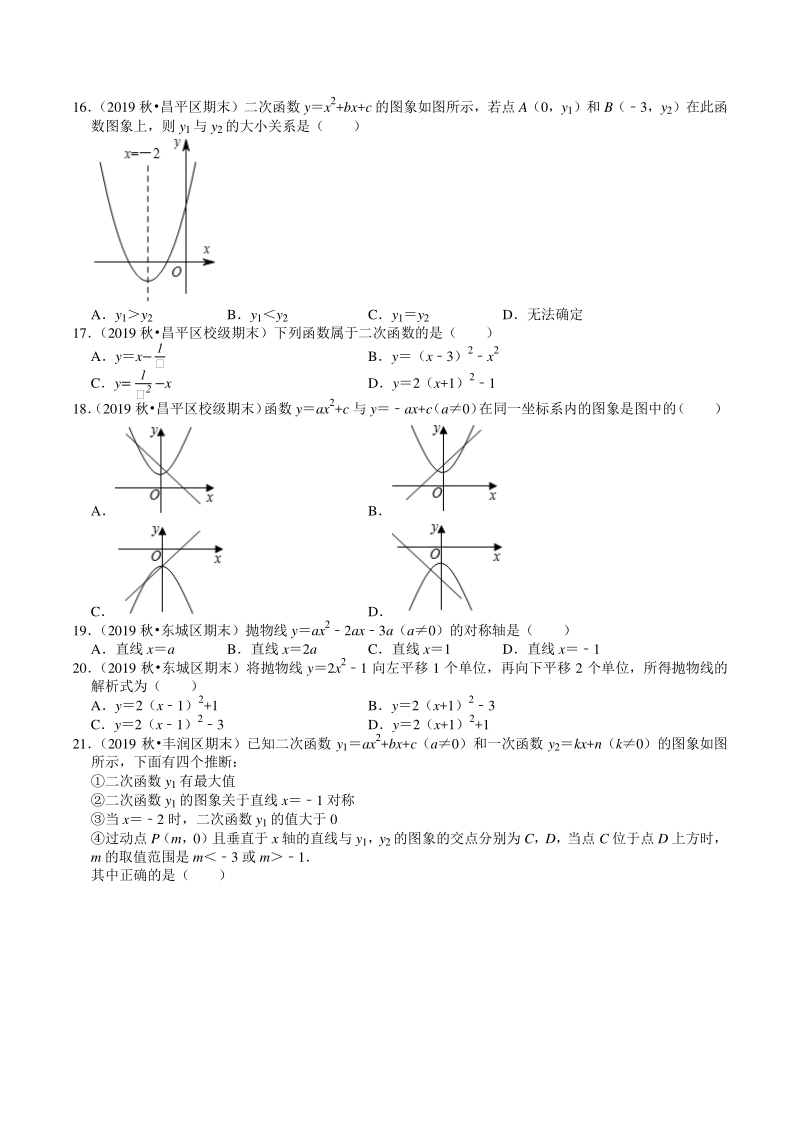
7、物线的表达式为（ ） Ay2（x+2）2+3 By2（x+2）23 Cy2（x2）23 Dy2（x2）2+3 14 （2019 秋西城区期末）在平面直角坐标系中，将抛物线 yx2向右平移 2 个单位长度，向上平移 1 个 单位长度，得到抛物线（ ） Ay（x2）2+1 By（x2）21 Cy（x+2）2+1 Dy（x+2）21 15 （2019 秋西城区期末）A（ 1 2，y1） ，B（1，y2） ，C（4，y3）三点都在二次函数 y（x2） 2+k 的 图象上，则 y1，y2，y3的大小关系为（ ） Ay1y2y3 By1y3y2 Cy3y1y2 Dy3y2y1 16 （2019 秋昌平区期
8、末）二次函数 yx2+bx+c 的图象如图所示，若点 A（0，y1）和 B（3，y2）在此函 数图象上，则 y1与 y2的大小关系是（ ） Ay1y2 By1y2 Cy1y2 D无法确定 17 （2019 秋昌平区校级期末）下列函数属于二次函数的是（ ） Ayx 1 By（x3）2x2 Cy= 1 2 x Dy2（x+1）21 18（2019 秋昌平区校级期末） 函数 yax2+c 与 yax+c （a0） 在同一坐标系内的图象是图中的 （ ） A B C D 19 （2019 秋东城区期末）抛物线 yax22ax3a（a0）的对称轴是（ ） A直线 xa B直线 x2a C直线 x1 D直线
9、 x1 20 （2019 秋东城区期末）将抛物线 y2x21 向左平移 1 个单位，再向下平移 2 个单位，所得抛物线的 解析式为（ ） Ay2（x1）2+1 By2（x+1）23 Cy2（x1）23 Dy2（x+1）2+1 21 （2019 秋丰润区期末）已知二次函数 y1ax2+bx+c（a0）和一次函数 y2kx+n（k0）的图象如图 所示，下面有四个推断： 二次函数 y1有最大值 二次函数 y1的图象关于直线 x1 对称 当 x2 时，二次函数 y1的值大于 0 过动点 P（m，0）且垂直于 x 轴的直线与 y1，y2的图象的交点分别为 C，D，当点 C 位于点 D 上方时， m 的取
10、值范围是 m3 或 m1 其中正确的是（ ） A B C D 22 （2019 秋密云区期末）抛物线 yx22 的顶点坐标为（ ） A （0，2） B （2，0） C （0，2） D （2，0） 23 （2019 秋昌平区校级期末）已知二次函数 yax2+bx+c 的图象如右图所示，则 a、b、c 满足（ ） Aa0，b0，c0 Ba0，b0，c0 Ca0，b0，c0 Da0，b0，c0 24 （2019 秋昌平区校级期末）若 y（m+1） 265是二次函数，则 m（ ） A7 B1 C1 或 7 D以上都不对 25 （2018 秋密云区期末）如图所示，点 A，B，C 是抛物线 yax2+bx
11、+c（a0） （x 为任意实数）上三点， 则下列结论： 2 =2 函数 yax2+bx+c 最大值大于 4 a+b+c2，其中正确的有（ ） A B C D 26 （2018 秋密云区期末）将抛物线 yx2向右平移 2 个单位，再向下平移 1 个单位，则平移后抛物线的 顶点坐标是（ ） A （2，1） B （2，1） C （2，1） D （2，1） 27 （2018 秋石景山区期末）将抛物线 yx2向下平移 2 个单位长度，得到的抛物线为（ ） Ayx2+2 Byx22 Cy（x2）2 Dy（x+2）2 28 （2018 秋顺义区期末）在平面直角坐标系 xOy 中，将抛物线 y2x2先向左平移
12、 3 个单位长度，再向下 平移 4 个单位长度后所得到的抛物线的表达式为（ ） Ay2（x+3）24 By2（x3）24 Cy2（x+3）2+4 Dy2（x3）2+4 29 （2018 秋平谷区期末）若二次函数 ykx24x+1 的图象与 x 轴有交点，则 k 的取值范围是（ ） Ak4 Bk4 Ck4 且 k0 Dk4 且 k0 30 （2018 秋西城区期末）下列关于二次函数 y2x2的说法正确的是（ ） A它的图象经过点（1，2） B它的图象的对称轴是直线 x2 C当 x0 时，y 随 x 的增大而减小 D当 x0 时，y 有最大值为 0 31 （2018 秋西城区期末）抛物线 y3（x
13、1）2+5 的顶点坐标是（ ） A （3，5） B （1，5） C （3，1） D （1，5） 32 （2018 秋平谷区期末）已知抛物线 yax2+bx+c（a0）与 x 轴交于点 A（1，0） ，对称轴为 x1， 与 y 轴的交点 B 在（0，2）和（0，3）之间（包含这两个点）运动有如下四个结论：抛物线与 x 轴 的另一个交点是（3，0） ；点 C（x1，y1） ，D（x2，y2）在抛物线上，且满足 x1x21，则 y1y2； 常数项 c 的取值范围是 2c3；系数 a 的取值范围是1a 2 3上述结论中，所有正确结论的序 号是（ ） A B C D 33 （2018 秋怀柔区期末）如图
14、，一条抛物线与 x 轴相交于 M，N 两点（点 M 在点 N 的左侧） ，其顶点 P 在线段 AB 上移动，点 A，B 的坐标分别为（2，3） ， （1，3） ，点 N 的横坐标的最大值为 4，则点 M 的横坐标的最小值为（ ） A1 B3 C5 D7 34 （2018 秋昌平区期末）科学家为了推测最适合某种珍奇植物生长的温度，将这种植物分别放在不同温 度的环境中，经过一定时间后，测试出这种植物高度的增长情况，部分数据如下表： 温度 t/ 5 3 2 植物高度增长量 h/mm 34 46 41 科学家推测出 h（mm）与 t 之间的关系可以近似地用二次函数来刻画已知温度越适合，植物高度增长 量
15、越大，由此可以推测最适合这种植物生长的温度为（ ） A2 B1 C0 D1 35 （2018 秋朝阳区期末）抛物线 y（x+2）21 的对称轴是（ ） Ax1 Bx1 Cx2 Dx2 36 （2018 秋北京期末） 心理学家发现： 课堂上， 学生对概念的接受能力 s 与提出概念的时间 t （单位： min） 之间近似满足函数关系 sat2+bt+c（a0） ，s 值越大，表示接受能力越强如图记录了学生学习某概念 时 t 与 s 的三组数据，根据上述函数模型和数据，可推断出当学生接受能力最强时，提出概念的时间为 （ ） A8min B13min C20min D25min 37 （2018 秋昌
16、平区期末）二次函数 yx22x，若点 A（1，y1） ，B（2，y2）是它图象上的两点，则 y1 与 y2的大小关系是（ ） Ay1y2 By1y2 Cy1y2 D不能确定 38 （2018 秋丰台区期末）将二次函数 yx24x+1 化成 ya（xh）2+k 的形式为（ ） Ay（x4）2+1 By（x4）23 Cy（x2）23 Dy（x+2）23 39 （2018 秋丰台区期末） 二次函数 yax2+bx+c （a0） 的图象如图所示， 那么下列说法正确的是 （ ） Aa0，b0，c0 Ba0，b0，c0 Ca0，b0，c0 Da0，b0，c0 40 （2018 秋门头沟区期末）二次函数 y
17、x2的对称轴是（ ） A直线 y1 B直线 x1 Cy 轴 Dx 轴 第第 22 章二次函数选择题精选章二次函数选择题精选 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 40 小题）小题） 1 【解答】解：二次函数 yx2+px+q（x+ 2） 2+42 4 ， 该抛物线的对称轴为 x= 2，且 a10， 当 x= 2 0， 当 x1 时，二次函数有最大值为：1+p+q8，即 p+q7， 当 x0 时，二次函数有最小值为：qt，即 t7p， 当 x= 2 1， 当 x0 时，二次函数有最大值为：q8， 当 x1 时，二次函数有最小值为：1+p+qt，即 t9+p， 当 0 2
18、 1 2 此时当 x1 时，函数有最大值 1+p+q8， 当 x= 2时，函数有最小值 q 2 4 =t，即 t7p 2 4 ， 1 2 2 1，当 x0 时，函数有最大值 q8，当 x= 2时，函数有最小值 q 2 4 =t，即 t8 2 4 ， x= 2 = 1 2，当 x0 或 1 时函数有最大值 q8， 当 x= 2时，函数有最小值 q 2 4 =t，即 t8 2 4 wst， w 的值与 p 有关，但与 q 无关， 故选：D 2 【解答】解：抛物线 y4x2向上平移 1 个单位长度得到抛物线的解析式为 y4x2+1， 故选：B 3 【解答】解：y（x3） （x5）（x4）21此时，该
19、抛物线顶点坐标是（4，1） 将该抛物线绕坐标原点 O 旋转 180后的顶点坐标是（4，1） 再向右平移 2 个单位长度后的顶点坐标 是（2，1） 所以此时抛物线的解析式为：y（x+2）2+1x24x3 故选：A 4 【解答】解：根据已知条件利用待定系数法可得： y1= 1 2（x 3 2） 2+33 8 ， y2= 5 4（x 3 2） 2+93 16， y3= 5 8（x1） 2+29 8 ， y4（x1）2+7x2+2x+6 y4 与 y 轴交点为（0，6） 四条抛物线的开口方向均向下； 当 x0 时，四条抛物线表达式中的 y 均随 x 的增大而增大； 抛物线 y1的顶点在抛物线 y2顶点
20、的下方； 抛物线 y4与 y 轴交点在点 B 的上方 所以正确 故选：A 5 【解答】解：抛物线 y（x1）24， 该抛物线的顶点坐标为（1，4） ， 故选：D 6 【解答】解：由“左加右减”的原则可知，将二次函数 y2x2的图象先向右平移 2 个单位所得函数的解 析式为：y2（x2）2； 由“上加下减”的原则可知，将二次函数 y2（x2）2的图象先向下平移 3 个单位所得函数的解析式 为：y2（x2）23 故选：C 7 【解答】解：由表格可知， + = 0 + + = 2 = 2 解得 = 1 = 1 = 2 抛物线的解析式为 yx2+x+2， a10，抛物线开口向下，正确； 抛物线的对称轴
21、是直线 x= 0+1 2 = 1 2，故正确， 抛物线的顶点坐标是（1 2， 9 4） ，故错误， 故选：A 8 【解答】解：观察二次函数 ykx2+2x+1 的部分图象可知： k0，且 44k0 即 k1， 解得 0k1 故选：D 9 【解答】解：最值在自变量大于 13.5 小于 14.7 之间， 所以最接近摩天轮转一圈的时间的是 15230 分钟 故选：B 10 【解答】解：观察图象可知： a0，b0，c0，abc0， 所以错误； 对称轴为直线 x1， 即 2 = 1，解得 b2a，即 2ab0， 所以错误； 抛物线 yax2+bx+c 经过点（1，0） ，且对称轴为直线 x1， 抛物线与
22、 x 轴的另一个交点为（3，0） ， 当 a3 时，y0，即 9a3b+c0， 所以正确； mn0， m1n11， 由 x1 时，y 随 x 的增大而减小知 xm1 时的函数值小于 xn1 时的函数值，故正确； 故选：D 11 【解答】解：A、将 y2x2+1 的图象向下平移 3 个单位得到 y2x22 的图象，故 A 选项不符合题 意； B、将 y2（x1）2的图象向左平移 3 个单位得到 y2（x+2）2的图象，故 B 选项不符合题意； C、将 y2x2的图象沿 x 轴翻折得到 y2x2的图象，故 C 选项不符合题意； D、将 y2（x1）2+1 的图象沿 y 轴翻折得到 y2（x+1）2
23、+1 的图象，故 D 选项符合题意 故选：D 12 【解答】解：A、由于 yx2+bx2 中 a10，所以该抛物线开口方向向上，故本选项不符合题意 B、令 x0，则 y2，所以抛物线与 y 轴交点的坐标为（0，2） ，故本选项不符合题意 C、当 b0 时，与 a 的符号相同，则抛物线的对称轴位于 y 轴的左侧，故本选项不符合题意 D、由于b2+80，所以该抛物线与 x 轴有两个公共点，故本选项符合题意 故选：D 13 【解答】解：抛物线 y2x2先向右平移 2 个单位长度，得：y2（x2）2； 再向上平移 3 个单位长度，得：y2（x2）2+3 故选：D 14 【解答】解：抛物线 yx2向右平
24、移 2 个单位长度，得：y（x2）2； 再向上平移 1 个单位长度，得：y（x2）2+1 故选：A 15 【解答】解：二次函数 y（x2）2+k 的图象开口向下，对称轴为 x2，点 A（ 1 2，y1） ，B（1，y2） 在对称轴的左侧，由 y 随 x 的增大而增大，有 y1y2， 由 x= 1 2，x1，x4 离对称轴 x2 的远近可得，y1y3，y3y2，因此有 y1y3y2， 故选：B 16 【解答】解：点 A（0，y1）和 B（3，y2）在抛物线对称轴 x2 的两侧，且点 A 比点 B 离对称轴要 远，因此 y1y2， 故选：A 17 【解答】解： A自变量 x 的次数不是 2，故 A
25、 错误； By（x3）2x2整理后得到 y6x+9，是一次函数，故 B 错误 C由 1 2 = 2可知，自变量 x 的次数不是 2，故 C 错误； Dy2（x+1）21 是二次函数的顶点式解析式，故 D 正确 故选：D 18 【解答】解：A、由二次函数 yax2+c 的图象可得：a0，c0，由函数 yax+c 的图象可得：a0， c0，函数 yax+c 与 yax2+c 的与坐标轴的交点是同一点，错误； B、由二次函数 yax2+c 的图象可得：a0，c0，由函数 yax+c 的图象可得：a0，c0，错误； C、由二次函数 yax2+c 图象可得：a0，c0，由函数 yax+c 的图象可得：a
26、0，c0，函数 y ax+c 与 yax2+c 的与坐标轴的交点是同一点，正确； D、由二次函数 yax2+c 的图象可得：a0，c0，由函数 yax+c 的图象可得：a0，c0，错误 故选：C 19 【解答】解：抛物线 yax22ax3a（a0）的对称轴是直线 x= 2 2 =1，即 x1 故选：C 20 【解答】解：按照“左加右减，上加下减”的规律，y 将抛物线 y2x21 向左平移 1 个单位，再向下 平移 2 个单位，所得抛物线的解析式为 y2（x+1）212，即 y2（x+1）23， 故选：B 21 【解答】解：二次函数 y1ax2+bx+c（a0）的图象的开口向上， 二次函数 y1
27、有最小值，故错误； 观察函数图象可知二次函数 y1的图象关于直线 x1 对称，故正确； 当 x2 时，二次函数 y1的值小于 0，故错误； 当 x3 或 x1 时，抛物线在直线的上方， m 的取值范围为：m3 或 m1，故正确 故选：D 22 【解答】解：抛物线 yx22 是顶点式， 根据顶点式的坐标特点可知， 顶点坐标为（0，2） ， 故选：A 23 【解答】解：二次函数的图象开口向上， a0， 二次函数的图象与 y 轴的交点在 y 轴的负半轴上， c0， 二次函数的对称轴在 y 轴的右边， 20， 2 0， a0， b0， 故选：B 24 【解答】解：由题意得：m26m52；且 m+10；
28、 解得 m7 或1；m1， m7， 故选：A 25 【解答】解：抛物线 yax2+bx+c（a0 的大致图象如有图 抛物线与 x 轴交于 C和 C，C介于 01 之间，设 C（t，0）其中 0t1 2 = +3 2 ，0t1，3 2 2 2因此错误； 由图象可知，图象顶点纵坐标在 4 的上方，所以函数最大值大于 4因此正确 由图象可知，x1 时，y3，即 a+b+c32因此正确 故选：B 26 【解答】解：将抛物线 yx2向右平移 2 个单位，再向下平移 1 个单位后的抛物线的解析式为：y（x 2）21 则平移后的抛物线的顶点坐标为： （2，1） 故选：B 27 【解答】解：抛物线 yx2的顶
29、点坐标为（0，0） ，把点（0，0）下平移 2 个单位长度所得对应点的坐标 为（0，2） ，所以平移后的抛物线为 yx22 故选：B 28 【解答】解：抛物线 y2x2的顶点坐标为（0，0） ，把点（0，0）先向左平移 3 个单位长度，再向下平 移 4 个单位长度后得到点的坐标为（3，4） ， 所以平移后所得的抛物线的解析式为 y2（x+3）24 故选：A 29 【解答】解：二次函数 ykx24x+1 的图象与 x 轴有交点， k0 且（4）24k0， k4 且 k0 故选：D 30 【解答】解：A、当 x1 时，y2（1）222，故此选项错误； B、它的图象的对称轴是直线 x0，故此选项错误
30、； C、当 x0 时，y 随 x 的增大而减小，当 x0 时，y 随 x 的增大而增大，故此选项正确； D、当 x0 时，y 有最小值是 0，故此选项错误； 故选：C 31 【解答】解：因为 y3（x1）2+5 是抛物线的顶点式， 根据顶点式的坐标特点可知，顶点坐标为（1，5） 故选：B 32 【解答】解：抛物线与 x 轴交于点 A（1，0） ，对称轴为 x1， 抛物线与 x 轴的另一个交点是（3，0） ，所以正确； 抛物线与 y 轴的交点 B 在（0，2）和（0，3）之间（包含这两个点）运动， 抛物线开口向上，2c3，所以正确； 当 x1 时，y 随 x 的增大而增大， 当 x1x21，y1
31、y2；所以错误； x= 2 =1， b2a， x1 时，y0，即 ab+c0， a+2a+c0，即 c3a， 而 2c3， 23a3， 1a 2 3，所以正确 故选：D 33 【解答】解：当图象顶点在点 B 时，点 N 的横坐标的最大值为 4， 则此时抛物线的表达式为：ya（x1）23， 把点 N 的坐标代入得：0a（41）23， 解得：a= 1 3， 当顶点在点 A 时，M 点的横坐标为最小， 此时抛物线的表达式为：y= 1 3（x+2） 23， 令 y0，则 x5 或 1， 即点 M 的横坐标的最小值为5， 故选：C 34 【解答】解：设 hat2+bt+c（a0） ， 将（5，34） ，
32、 （3，46） ， （2，41）代入方程组： 得： 25 5 + = 34 9 3 + = 46 4 + 2 + = 41 ， 解得： = 1 = 2 = 49 ， 所以 h 与 t 之间的二次函数解析式为：ht22t+49（t+1）2+50， 当 t1 时，y 有最大值 50， 即说明最适合这种植物生长的温度是1 故选：B 35 【解答】解：抛物线 y（x+2）21 的对称轴是直线 x2， 故选：C 36 【解答】解：由题意得：函数过点（0，43） 、 （20，55） 、 （30，31） ， 把以上三点坐标代入 sat2+bt+c 得： 43 = 55 = 202 + 20 + 31 = 3
33、02 + 30 + ，解得： = 1 10 = 13 5 = 43 ， 则函数的表达式为：s= 1 10t 2+13 5 t+43， a= 1 100，则函数有最大值， 当 t= 2 =13 时，s 有最大值，即学生接受能力最强， 因此 B 正确； 备注：本题为选择题，为此可用函数的对称性来解答，从图象看，函数的对称轴大概是在 10 到 15 之间 的，所以答案是 B，这样判断较为简便，可参考 故选：B 37 【解答】解：当 x1 时，y1x22x3； 当 x2 时，y2x22x0； 30， y1y2， 故选：C 38 【解答】解：yx24x+1 （x24x+4）+14 （x2）23 所以把二次函数 yx24x+1 化成 ya（xh）2+k 的形式为：y（x2）23 故选：C 39 【解答】解：抛物线开口向下， a0， 抛物线的对称轴在 y 轴的右侧， x= 20， b0， 抛物线与 y 轴的交点在 x 轴上方， c0， 故选：B 40 【解答】解：二次函数 yx2的对称轴是直线 x0，即 y 轴， 故选：C
