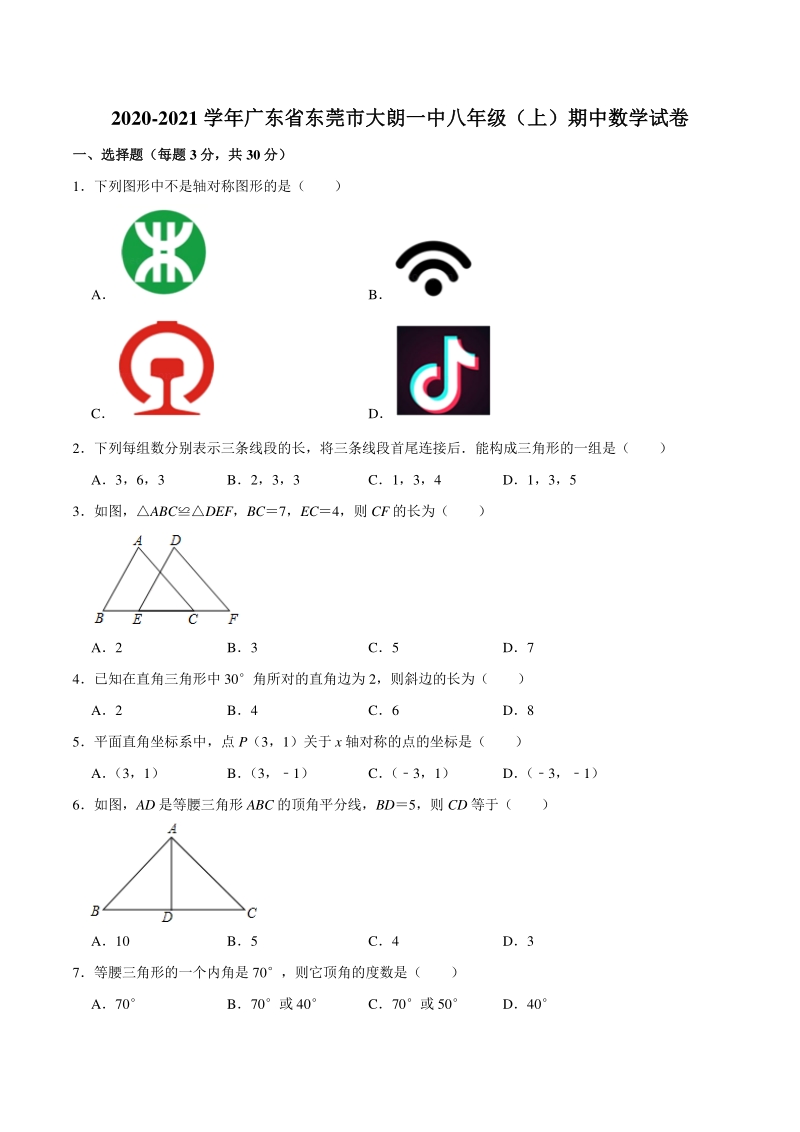
1、2020-2021 学年广东省东莞市大朗一中八年级（上）期中数学试卷学年广东省东莞市大朗一中八年级（上）期中数学试卷 一、选择题（每题一、选择题（每题 3 分，共分，共 30 分）分） 1下列图形中不是轴对称图形的是（ ） A B C D 2下列每组数分别表示三条线段的长，将三条线段首尾连接后能构成三角形的一组是（ ） A3，6，3 B2，3，3 C1，3，4 D1，3，5 3如图，ABCDEF，BC7，EC4，则 CF 的长为（ ） A2 B3 C5 D7 4已知在直角三角形中 30角所对的直角边为 2，则斜边的长为（ ） A2 B4 C6 D8 5平面直角坐标系中，点 P（3，1）关于 x
2、 轴对称的点的坐标是（ ） A （3，1） B （3，1） C （3，1） D （3，1） 6如图，AD 是等腰三角形 ABC 的顶角平分线，BD5，则 CD 等于（ ） A10 B5 C4 D3 7等腰三角形的一个内角是 70，则它顶角的度数是（ ） A70 B70或 40 C70或 50 D40 8如图ABC 中，A85，B38，则ACD 为（ ） A67 B95 C123 D142 9如图，在ABC 中，ABC 和ACB 的角平分线交于点 E，过点 E 作 MNBC 交 AB 于点 M，交 AC 于 点 N若 BM2，CN3，则 MN 的长为（ ） A10 B5.5 C6 D5 10 如
3、图， AD 平分BAC， DEAB 于点 E， DFAC 于点 F， 连接 EF 交 AD 于点 G， 则下列结论： DF+AE AD；DEDF；ADEF；SABD：SACDAB：AC，其中正确结论的个数是（ ） A1 个 B2 个 C3 个 D4 个 二、填空题（每小题二、填空题（每小题 4 分，共分，共 28 分）分） 11 （4 分）在ABC 中，若C90，B35，则A 的度数为 12 （4 分）一个正多边形的每个外角都是 36，这个正多边形的边数是 13 （4 分）如图，OAOB 点 C、点 D 分别在 OA、OB 上，BC 与 AD 交于点 E，要使AODBOC，则 需要添加的一个条
4、件是 （写出一个即可） 14（4分） 如图， 已知ABC中， BC4， AB的垂直平分线交AC于点D， 若AC6， 则BCD的周长 15 （4 分）如图，在 RtABC 中，ACB90，AD 平分BAC 交 BC 于点 D，若 AB5，DC2，则 ABD 的面积为 16 （4 分）如图，ABCADE，D 在 BC 边上，EAC40，则B 的度数为 17 （4 分）如图，在ABC 中，A64，ABC 和ACD 的平分线交于点 A1，得A1；A1BC 和 A1CD 的平分线交于点 A2，得A2；A2BC 和A2CD 的平分线交于点 A3，则A5 三、解答题（每小题三、解答题（每小题 6 分，共分，
5、共 18 分）分） 18 （6 分）如图，点 C 是 AB 的中点，ADCE，CDBE求证：ACDCBE 19 （6 分）ABC 中，BA+10，CB+10，求A 的度数 20 （6 分）已知：如图，ABC 中，AD 是高，AE 平分BAC，B50，C80 （1）求DAC 的度数； （2）求AED 的度数 四解答题（每小题四解答题（每小题 8 分，共分，共 24 分）分） 21 （8 分）如图，ABAC，A40 （1）尺规作图：求作线段 AB 的垂直平分线，交 AC 于点 D，交 AB 于点 E （保留作图痕迹） （2）求DBC 的度数 22 （8 分）如图所示，已知点 D 为ABC 的边 B
6、C 的中点，DEAC，DFAB，垂足分别为点 E，F且 BFCE求证： （1）BC； （2）AD 平分BAC 23 （8 分）如图，ACB90，ACBC，ADCE，BECE，垂足分别为 D，E （1）求证：CEBADC； （2）若 AD2.5cm，DE1.7cm，求 BE 的长 五、解答题（每小题五、解答题（每小题 10 分，共分，共 20 分）分） 24 （10 分）如图，在ABC 中，ABACBC，以点 A 为圆心，线段 AB 的长为半径画弧，与 BC 边交于 点 D，连接 AD 过点 D 作 DEAD，交 AC 于点 E （1）若B50，C28，求AED 度数； （2）若点 F 是 BD
7、 的中点，连接 AF，求证：BAFEDC 25 （10 分）图 1、图 2 中，点 C 为线段 AB 上一点，ACM 与CBN 都是等边三角形 （1）如图 1，线段 AN 与线段 BM 是否相等？证明你的结论； （2）线段 AN 与线段 BM 交于点 O，求AOM 的度数； （3）如图 2，AN 与 MC 交于点 E，BM 与 CN 交于点 F，探究CEF 的形状，并证明你的结论 2020-2021 学年广东省东莞市大朗一中八年级（上）期中数学试卷学年广东省东莞市大朗一中八年级（上）期中数学试卷 参考答案与试题解析参考答案与试题解析 一、选择题（每题一、选择题（每题 3 分，共分，共 30 分
8、）分） 1下列图形中不是轴对称图形的是（ ） A B C D 【分析】根据轴对称图形的概念求解 【解答】解：A、是轴对称图形，故本选项错误； B、是轴对称图形，故本选项错误； C、是轴对称图形，故本选项错误； D、不是轴对称图形，故本选项正确 故选：D 2下列每组数分别表示三条线段的长，将三条线段首尾连接后能构成三角形的一组是（ ） A3，6，3 B2，3，3 C1，3，4 D1，3，5 【分析】利用三角形的三边关系可得答案 【解答】解：A、3+36，不能组成三角形，故此选项不合题意； B、2+33，能组成三角形，故此选项符合题意； C、1+34，不能组成三角形，故此选项不合题意； D、1+3
9、5，不能组成三角形，故此选项不合题意； 故选：B 3如图，ABCDEF，BC7，EC4，则 CF 的长为（ ） A2 B3 C5 D7 【分析】利用全等三角形的性质可得 EFBC7，再解即可 【解答】解：ABCDEF， EFBC7， EC4， CF3， 故选：B 4已知在直角三角形中 30角所对的直角边为 2，则斜边的长为（ ） A2 B4 C6 D8 【分析】根据在直角三角形中，30角所对的直角边等于斜边的一半解答 【解答】解：在 RtABC 中，C90，A30，BC2， AB2BC224， 故选：B 5平面直角坐标系中，点 P（3，1）关于 x 轴对称的点的坐标是（ ） A （3，1） B
10、 （3，1） C （3，1） D （3，1） 【分析】关于 x 轴对称的点，横坐标相同，纵坐标互为相反数，可得答案 【解答】解：点 P（3，1）关于 x 轴对称的点的坐标是（3，1） 故选：B 6如图，AD 是等腰三角形 ABC 的顶角平分线，BD5，则 CD 等于（ ） A10 B5 C4 D3 【分析】根据等腰三角形三线合一的性质即可求解 【解答】解：AD 是等腰三角形 ABC 的顶角平分线，BD5， CD5 故选：B 7等腰三角形的一个内角是 70，则它顶角的度数是（ ） A70 B70或 40 C70或 50 D40 【分析】首先要进行分析题意， “等腰三角形的一个内角”没明确是顶角还
11、是底角，所以要分两种情况进 行讨论 【解答】解：本题可分两种情况： 当 70角为底角时，顶角为 18027040； 70角为等腰三角形的顶角； 因此这个等腰三角形的顶角为 40或 70 故选：B 8如图ABC 中，A85，B38，则ACD 为（ ） A67 B95 C123 D142 【分析】根据三角形外角性质解答即可 【解答】解：在ABC 中，A85，B38， ACDA+B85+38123， 故选：C 9如图，在ABC 中，ABC 和ACB 的角平分线交于点 E，过点 E 作 MNBC 交 AB 于点 M，交 AC 于 点 N若 BM2，CN3，则 MN 的长为（ ） A10 B5.5 C6
12、 D5 【分析】由平行线的性质，得出MEBCBE，NECBCE，再由角平分线定义得出MBE EBC，NCEBCE，证出 MEMB，NENC，即可求得 MN 的长 【解答】解：MNBC， MEBCBE，NECBCE， 在ABC 中，ABC 和ACB 的平分线交于点 E， MBEEBC，NCEBCE， MEBMBE，NECNCE， MEMB，NENC， MNME+NEBM+CN2+35， 故选：D 10 如图， AD 平分BAC， DEAB 于点 E， DFAC 于点 F， 连接 EF 交 AD 于点 G， 则下列结论： DF+AE AD；DEDF；ADEF；SABD：SACDAB：AC，其中正确
13、结论的个数是（ ） A1 个 B2 个 C3 个 D4 个 【分析】根据角平分线的性质得出 DEDF，根据全等三角形的判定推出 RtAEDRtAFD，根据全 等三角形的性质得出 AEAF，再逐个判断即可 【解答】解：AD 平分BAC，DEAB 于点 E，DFAC 于点 F， AEDAFD90，DEDF，故正确； 在 RtAED 和 RtAFD 中 ， RtAEDRtAFD（HL） ， AEAF， AD 平分BAC， ADEF，故正确； 在AFD 中，AF+DFAD， 又AEAF， AE+DFAD，故正确； SABD，SACD，DEDF， SABD：SACDAB：AC，故正确； 即正确的个数是
14、4 个， 故选：D 二、填空题（每小题二、填空题（每小题 4 分，共分，共 28 分）分） 11 （4 分）在ABC 中，若C90，B35，则A 的度数为 55 【分析】根据直角三角形的性质解答即可 【解答】解：在 RtABC 中，C90，B35， A903555， 故答案是：55 12 （4 分）一个正多边形的每个外角都是 36，这个正多边形的边数是 10 【分析】多边形的外角和等于 360，因为所给多边形的每个外角均相等，故又可表示成 36n，列方程 可求解 【解答】解：设所求正 n 边形边数为 n， 则 36n360， 解得 n10 故正多边形的边数是 10 13 （4 分）如图，OAO
15、B 点 C、点 D 分别在 OA、OB 上，BC 与 AD 交于点 E，要使AODBOC，则 需要添加的一个条件是 ODOC 或AB 或ADOBCO （写出一个即可） 【分析】由于AODBOC，OAOB，则可利用”SAS“或”ASA“或”AAS“添加条件 【解答】解：AODBOC， 而 OAOB， 当添加 ODOC 时，可根据”SAS“判断AODBOC； 当添加AB 时，可根据”ASA“判断AODBOC； 当添加ADOBCO 时，可根据”AAS“判断AODBOC； 综上所述，添加的条件为 ODOC 或AB 或ADOBCO 故答案为 ODOC 或AB 或ADOBCO 14 （4 分）如图，已知A
16、BC 中，BC4，AB 的垂直平分线交 AC 于点 D，若 AC6，则BCD 的周长 10 【分析】根据线段的垂直平分线的性质得到 DADB，根据三角形的周长公式计算即可 【解答】解：DE 是线段 AB 的垂直平分线， DADB， BCD 的周长 BC+CD+DB BC+CD+DA BC+AC 10， 故答案为：10 15 （4 分）如图，在 RtABC 中，ACB90，AD 平分BAC 交 BC 于点 D，若 AB5，DC2，则 ABD 的面积为 5 【分析】作 DHAB 于 H，如图，根据角平分线的性质得到 DHDC2，然后根据三角形面积公式计 算 【解答】解：作 DHAB 于 H，如图，
17、 AD 平分BAC，DHAB，DCAC， DHDC2， ABD 的面积525 故答案为 5 16 （4 分）如图，ABCADE，D 在 BC 边上，EAC40，则B 的度数为 70 【分析】 根据全等三角形的性质得到BACDAE， ADAB， 根据等腰三角形的性质计算， 得到答案 【解答】解：ABCADE， BACDAE，ADAB， BACDACDAEDAC，即BADEAC40， ABAD， BADB70， 故答案为：70 17 （4 分）如图，在ABC 中，A64，ABC 和ACD 的平分线交于点 A1，得A1；A1BC 和 A1CD 的平分线交于点 A2，得A2；A2BC 和A2CD 的平
18、分线交于点 A3，则A5 2 【分析】根据角平分线的定义可得A1BCABC，A1CDACD，再根据三角形的一个外角等 于与它不相邻的两个内角的和可得ACDA+ABC，A1CDA1BC+A1，整理即可求出A1 的度数，同理求出A2，可以发现后一个角等于前一个角的，根据发现后一个角等于前一个角的的 规律即可得解，把A64代入AnA 解答即可 【解答】解：A1B 是ABC 的平分线，A1C 是ACD 的平分线， A1BCABC，A1CDACD， 又ACDA+ABC，A1CDA1BC+A1， （A+ABC）ABC+A1， A1A， 同理可得A2A1AA， 由此可得一下规律：AnA， 当A64时，A5A
19、2， 故答案为：2 三、解答题（每小题三、解答题（每小题 6 分，共分，共 18 分）分） 18 （6 分）如图，点 C 是 AB 的中点，ADCE，CDBE求证：ACDCBE 【分析】由已知条件 ADCE，CDBE，和 ACCB，根据三角形全等的判定定理 SSS 可证得ACD CBE 【解答】证明：点 C 是 AB 的中点， ACCB 在ACD 和CBE 中， （5 分） ACDCBE（SSS） （6 分） 19 （6 分）ABC 中，BA+10，CB+10，求A 的度数 【分析】将第一个等式代入第二等式用A 表示出C，再根据三角形的内角和等于 180列方程求出 A，然后求解即可 【解答】解
20、：BA+10，CB+10， CA+10+10A+20， 由三角形内角和定理得，A+B+C180， 所以，A+A+10+A+20180， 解得A50 20 （6 分）已知：如图，ABC 中，AD 是高，AE 平分BAC，B50，C80 （1）求DAC 的度数； （2）求AED 的度数 【分析】 （1）根据三角形的内角和定理，可求得BAC 的度数，由 AE 是BAC 的平分线，可得EAC 的度数，在直角ADC 中，可求出DAC 的度数； （2）得出DAEEACDAC，进而即可解答 【解答】解： （1）ABC 中，B50，C80， BAC180BC 1805080 50， AE 是BAC 的平分线，
21、 EACBAC25， AD 是 BC 边上的高， 在直角ADC 中， DAC90C908010， （2）DAC10， DAEEACDAC251015， AED90DAE901575 四解答题（每小题四解答题（每小题 8 分，共分，共 24 分）分） 21 （8 分）如图，ABAC，A40 （1）尺规作图：求作线段 AB 的垂直平分线，交 AC 于点 D，交 AB 于点 E （保留作图痕迹） （2）求DBC 的度数 【分析】 （1）依据垂直平分线的尺规作图方法，即可得到 AB 的垂直平分线； （2）依据等腰三角形的性质，即可得到ABC 的度数，再根据垂直平分线的性质，即可得到ABD 的 度数，进
22、而得出DBC 的度数 【解答】解： （1）如图所示，DE 即为所求； （2）ABAC，A40， ABC70， 又DE 垂直平分 AB， ADBD， ABDA40， DBCABCABD704030 22 （8 分）如图所示，已知点 D 为ABC 的边 BC 的中点，DEAC，DFAB，垂足分别为点 E，F且 BFCE求证： （1）BC； （2）AD 平分BAC 【分析】 （1）由中点的定义得出 BDCD，由 HL 证明 RtBDFRtCDE，得出对应角相等即可 （2）根据等腰三角形的三线合一即可解决问题； 【解答】证明： （1）点 D 是ABC 的边 BC 的中点， BDCD， DEAC，DFA
23、B， BFDCED90， 在 RtBDF 和 RtCDE 中， ， RtBDFRtCDE（HL） ， BC （2）BC， ABAC， BDDC， AD 平分BAC 23 （8 分）如图，ACB90，ACBC，ADCE，BECE，垂足分别为 D，E （1）求证：CEBADC； （2）若 AD2.5cm，DE1.7cm，求 BE 的长 【分析】 （1）由 ADCE，BECE，可以得到BECCDA90，再根据ACB90，可以得到 BCECAD，然后即可证明结论成立； （2）根据（1）中的结论和 AD2.5cm，DE1.7cm，可以求得 BE 的长 【解答】 （1）证明：ACB90，BECE，ADCE
24、， BCE+DCA90，BECCDA90， ACD+BCE90， BCECAD， 在CEB 和ADC 中， ， CEBADC（AAS） ； （2）解：CEBADC， BECD，CEAD2.5cm DCCEDE，DE1.7cm， DC2.51.70.8cm， BE0.8cm 五、解答题（每小题五、解答题（每小题 10 分，共分，共 20 分）分） 24 （10 分）如图，在ABC 中，ABACBC，以点 A 为圆心，线段 AB 的长为半径画弧，与 BC 边交于 点 D，连接 AD 过点 D 作 DEAD，交 AC 于点 E （1）若B50，C28，求AED 度数； （2）若点 F 是 BD 的中
25、点，连接 AF，求证：BAFEDC 【分析】 （1）由题意可得 ABAD，求得ADBB50，根据平角的定义得到EDC180 ADBADE180509040，根据三角形外角的性质即可得到结论； （2） 根据等腰三角形的性质得到 AFBD， BAFDAF， 由三角形的内角和得到DAF+ADB90， 由平角的定义得到ADF+EDC90，于是得到结论 【解答】解： （1）由题意可得 ABAD， ADBB50， DEAD， ADE90， EDC180ADBADE180509040， C28， AEDEDC+C40+2868； （2）ABAD，点 F 是 BD 的中点， AFBD，BAFDAF， DAF+
26、ADB90 DEAD， ADE90， ADF+EDC90， DAFEDC， BAFEDC 25 （10 分）图 1、图 2 中，点 C 为线段 AB 上一点，ACM 与CBN 都是等边三角形 （1）如图 1，线段 AN 与线段 BM 是否相等？证明你的结论； （2）线段 AN 与线段 BM 交于点 O，求AOM 的度数； （3）如图 2，AN 与 MC 交于点 E，BM 与 CN 交于点 F，探究CEF 的形状，并证明你的结论 【分析】 （1）证ACNMCB（SAS） ，即可得出 ANBM； （2）由全等三角形的性质得ANCMBC，则AOMCAN+MBCCAN+ANCBCN 60； （3）证A
27、CEMCF（ASA） ，得 CECF，即可得出结论 【解答】解： （1）ANBM，理由如下： ACM、CBN 都是等边三角形， ACCM，CNCB，ACMBCN60， ACM+MCNBCN+MCN， ACNBCM， 在ACN 和MCB 中， ， ACNMCB（SAS） ， ANBM； （2）由（1）得：ACNMCB， ANCMBC， AOMCAN+MBCCAN+ANCBCN60； （3）CEF 是等边三角形，理由如下： ACNMCB， CAECMF， MCF180ACMBCN60， ACEMCF， 在ACE 和MCF 中， ， ACEMCF（ASA） ， CECF， MCF60， CEF 是等边三角形
