1、 1 第 20 讲 图形的平移、对称与旋转 【考点导引】 1.理解轴对称、轴对称图形、中心对称、中心对称图形、平移和图形旋转的概念，并掌握它们的性质 2能按平移、旋转或对称的要求作出简单的图形 3探索成轴对称或中心对称的平面图形的性质 4运用图形的轴对称、旋转、平移进行图案设计. 【难点突破】 1. 点的坐标在变换中的规律： （1）平移：左右平移时横坐标左减右加，纵坐标不变；上下平移时纵坐标上 加下减，横坐标不变； （2）关于坐标轴对称，与其同名的坐标不变，另一个坐标变为相反数； （3）关于原 点对称，其坐标互为相反数； （4）点(x，y)关于原点顺时针旋转 90 后的点坐标为(y，x)，点(
2、x，y)关于原 点逆时针旋转 90 后的点坐标为(y， x) 注意： 研究有关点旋转时点的坐标变化规律时， 若旋转方向不明， 需分顺时针和逆时针两种情况进行讨论 2. （1）轴对称图形是指一个图形沿某条直线折叠后，直线两旁的部分能够完全重合的图形，注意与中心对 称图形区分开来，中心对称图形是指一个图形绕某个点旋转 180 后能与自身重合的图形中心对称图形的 对称中心是一个点，轴对称图形的对称轴是直线；中心对称图形的对称中心只有一个，而轴对称图形的对 称轴可能有多条一般地，正偶数多边形既是中心对称图形又是轴对称图形，正奇数多边形是轴对称图形 但不是中心对称图形，它们的对称轴条数和边数一致 （2）
3、轴对称图形与轴对称、中心对称图形与中心对称，是不同的概念，不要把它们混淆 3. 应用轴对称的性质构造全等三角形，揭示图形中隐含的相等线段或相等的角，对于图形中隐含的几个点 到某一定点的距离相等，往往构造圆，应用圆的性质解决问题比较简便。 4. 识别中心对称图形的方法是根据概念，将这个图形绕某一点旋转 180 ，如果旋转后的图形能够与自身重 合，那么这个图形就是中心对称图形，这个点是对称中心而识别轴对称图形的方法是把一个图形沿着一 条直线翻折，如果直线两旁的部分能够完全重合，那么这个图形就是轴对称图形 【解题策略】 转化思想：有关几条线段之和最短的问题，都是把它们转化到同一条直线上，然后利用“两
4、点之间线段最短” 来解决 【典例精析】 类型一：轴对称图形与中心对称图形的识别 【例 1】(2019云南4 分)下列图形既是轴对称图形，又是中心对称图形的是( ) 2 A B C D 【答案】D 【解答】解：根据轴对称和中心对称定义可知，A 选项是轴对称，B 选项既是轴对称又是中心对称，C 选项 是轴对称，D 选项是轴对称图形，故选 D 类型二：图形的平移 【例 2】 （2019湖北省随州市3 分） 如图， 在平面直角坐标系中， RtABC 的直角顶点 C 的坐标为 （1， 0） ， 点 A 在 x 轴正半轴上，且 AC=2将ABC 先绕点 C 逆时针旋转 90 ，再向左平移 3 个单位，则变
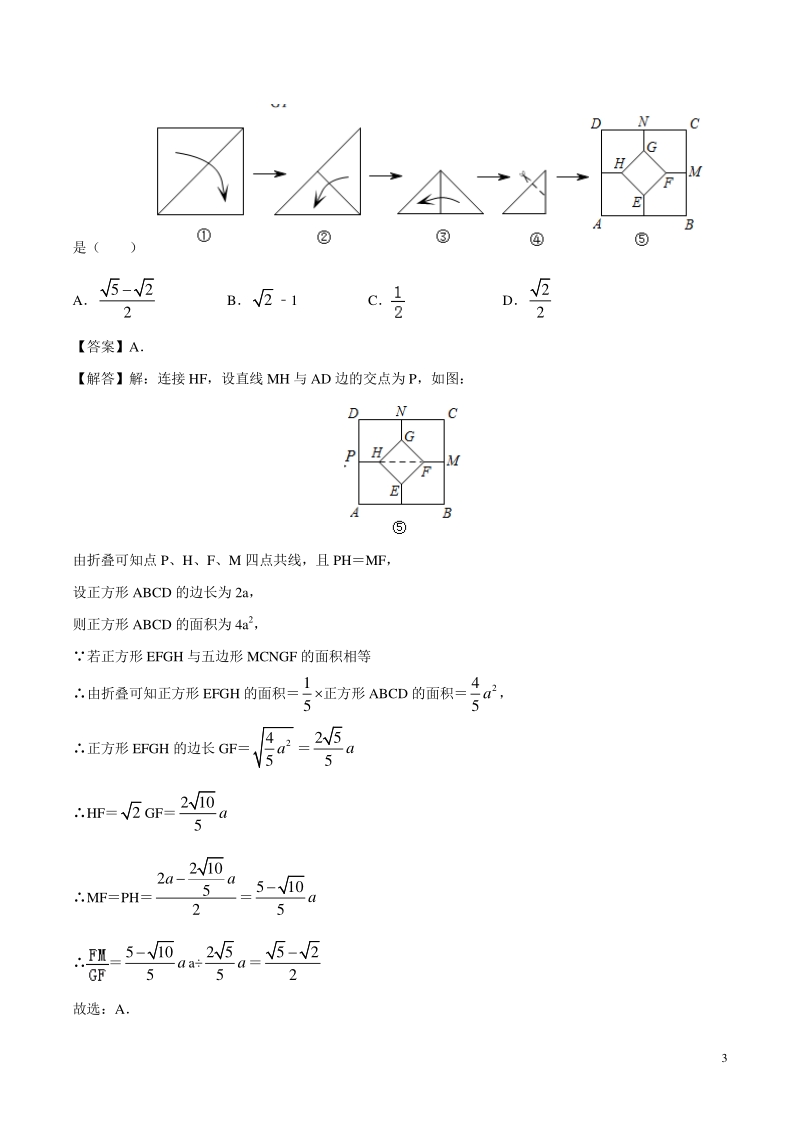
5、换后点 A 的对应点的坐标为_ 【答案】（-2，2） 【解析】解：点 C 的坐标为（1，0），AC=2， 点 A 的坐标为（3，0）， 如图所示，将 RtABC 先绕点 C 逆时针旋转 90 ， 则点 A的坐标为（1，2）， 再向左平移 3 个单位长度，则变换后点 A的对应点坐标为（-2，2），故答案为：（-2，2） 类型三：图形的对称 【例 3】 （2019 浙江丽水 3 分）将一张正方形纸片按如图步骤，通过折叠得到图，再沿虚线剪去一个角， 展开铺平后得到图，其中 FM，GN 是折痕若正方形 EFGH 与五边形 MCNGF 的面积相等，则的值 3 是（ ） A 52 2 B21 C D 2
6、2 【答案】A 【解答】解：连接 HF，设直线 MH 与 AD 边的交点为 P，如图： 由折叠可知点 P、H、F、M 四点共线，且 PHMF， 设正方形 ABCD 的边长为 2a， 则正方形 ABCD 的面积为 4a2， 若正方形 EFGH 与五边形 MCNGF 的面积相等 由折叠可知正方形 EFGH 的面积 1 5 正方形 ABCD 的面积 2 4 5 a， 正方形 EFGH 的边长 GF 2 4 5 a 2 5 5 a HF2GF 2 10 5 a MFPH 2 10 2 5 2 aa 510 5 a 510 5 a a2 5 5 a 52 2 故选：A 4 类型四：图形的旋转 【例 4】
7、 （2019湖北省荆门市3 分）如图，RtOCB 的斜边在 y 轴上，OC3，含 30 角的顶点与原点重 合，直角顶点 C 在第二象限，将 RtOCB 绕原点顺时针旋转 120 后得到OCB，则 B 点的对应点 B的坐 标是（ ） A （3，1） B （1，3） C （2，0） D （3，0） 【答案】A 【解答】解：如图， 在 RtOCB 中，BOC30 ， BC 3 3 OC 3 3 31， RtOCB 绕原点顺时针旋转 120 后得到OCB， OCOC3，BCBC1，BCOBCO90 ， 点 B的坐标为（3，1） 故选：A 类型五：平移、旋转作图 【例 5】（2019广西北部湾8 分）如
8、图，在平面直角坐标系中，已知ABC 的三个顶点坐标分别是 A（2， 1） 、B（1，2） 、C（3，3）. （1）将ABC 向上平移 4 个单位长度得到A1B1C1，请画出A1B1C1; 5 （2）请画出ABC 关于 y 轴对称的A2B2C2; （3）请写出 A1、A2的坐标. 【答案】解：（1）如图所示：A1B1C1，即为所求； （2）如图所示：A2B2C2，即为所求； （3）A1（2，3），A2（-2，-1） 【解析】 （1）直接利用平移的性质得出对应点位置进而得出答案； （2）直接利用轴对称的性质得出对应点位置进而得出答案； （3）利用所画图象得出对应点坐标 此题主要考查了轴对称变换以及
9、平移变换，正确得出对应点位置是解题关键 【例题 6】(2019浙江丽水12 分)如图，在等腰 RtABC 中，ACB90 ，AB214，点 D，E 分别在 边 AB，BC 上，将线段 ED 绕点 E 按逆时针方向旋转 90 得到 EF (1)如图 1，若 ADBD，点 E 与点 C 重合，AF 与 DC 相交于点 O求证：BD2DO (2)已知点 G 为 AF 的中点 如图 2，若 ADBD，CE2，求 DG 的长 6 若 AD6BD，是否存在点 E，使得DEG 是直角三角形？若存在，求 CE 的长；若不存在，试说明理由 【答案】(1)见证明过程 (2) 5 2 2 6 22或 18214或
10、2 【解答】(1)证明：如图 1，CACB，ACB90 ，BDAD， CDAB，CDADBD， CDCF，ADCF， ADCDCF90 ，ADCF， 四边形 ADFC 是平行四边形，ODOC， BD2OD (2)解：如图 2，作 DTBC 于点 T，FHBC 于 H 由题意：BDADCD72，BC2BD14， DTBC，BTTC7， EC2，TE5， DTEEHFDEF90 ， 7 DET+TDE90 ，DET+FEH90 ，TDEFEH， EDEF，DTEEHF(AAS)，FHET5， DDBEDFE45 ，B，D，E，F 四点共圆， DBF+DEF90 ，DBF90 ， DBE45 ，FB
11、H45 ， BHF90 ，HBFHFB45 ， BHFH5，BF52， ADCABF90 ，DGBF， ADDB，AGGF， DG 1 2 BF 5 2 2 解：如图 31 中，当DEG90 时，F，E，G，A 共线，作 DTBC 于点 T，FHBC 于 H设 ECx AD6BD，BDAB22， DTBC，DBT45 ，DTBT2， DTEEHF，EHDT2，BHFH12x， FHAC， 14 122x x ， 整理得：x212x+280，解得 x6 22 如图 32 中，当EDG90 时，取 AB 的中点 O，连接 OG作 EHAB 于 H 8 设 ECx，由 2可知 BF2 (12x)，O
12、G 1 2 BF 2 2 (12x)， EHDEDGDOG90 ， ODG+OGD90 ，ODG+EDH90 ，DGOHDE， EHDDOG， ， 整理得：x236x+2680，解得 x182或 18+2(舍弃)， 如图 33 中，当DGE90 时，取 AB 的中点 O，连接 OG，CG，作 DTBC 于 T，FHBC 于 H，EK CG 于 K设 ECx DBEDFE45 ，D，B，F，E 四点共圆，DBF+DEF90 ， DEF90 ，DBF90 ， AOOB，AGGF，OGBF， AOGABF90 ，OGAB， OG 垂直平分线段 AB，CACB，O，G，C 共线， 由DTEEHF，可得
13、 EHDTBT2，ETFH12x，BF2 (12x)， OGBF 2 2 (12x)，CKEK 2 2 x，GK72 2 2 (12x) 2 2 x， 由OGDKEG，可得， ，解得 x2 综上所述，满足条件的 EC 的值为 6 22或 18214或 2 9 【真题检测】 1. （2019四川省达州市3 分）剪纸是我国传统的民间艺术，下列剪纸作品中，轴对称图形是（ ） AB C D 【答案】D 【解答】解：A、不是轴对称图形，故此选项不合题意； B、不是轴对称图形，故此选项不合题意； C、不是轴对称图形，故此选项不合题意； D、是轴对称图形，故此选项符合题意； 故选：D 2. （2019，山东
14、枣庄，3 分）在平面直角坐标系中，将点 A（1，2）向上平移 3 个单位长度，再向左平 移 2 个单位长度，得到点 A，则点 A的坐标是（ ） A （1，1） B （1，2） C （1，2） D （1，2） 【答案】A 【解答】解：将点 A（1，2）向上平移 3 个单位长度，再向左平移 2 个单位长度，得到点 A， 点 A的横坐标为 121，纵坐标为2+31， A的坐标为（1，1） 故选：A 10 3. （2019 湖北宜昌 3 分）如图，平面直角坐标系中，点 B 在第一象限，点 A 在 x 轴的正半轴上，AOB B30 ，OA2，将AOB 绕点 O 逆时针旋转 90 ，点 B 的对应点 B的
15、坐标是（ ） A （1，2+3） B （3，3） C （3，2+3） D （3，3） 【答案】B 【解答】解：如图，作 BHy 轴于 H 由题意：OAAB2，BAH60 ， AHAB1，BH3， OH3， B（3，3） ， 故选：B 4. （2019河北省2 分）对于题目：“如图 1，平面上，正方形内有一长为 12、宽为 6 的矩形，它可以在正 方形的内部及边界通过移转（即平移或旋转）的方式，自由地从横放移转到竖放，求正方形边长的最小整 数 n”甲、乙、丙作了自认为边长最小的正方形，先求出该边长 x，再取最小整数 n 甲：如图 2，思路是当 x 为矩形对角线长时就可移转过去；结果取 n13 乙
16、：如图 3，思路是当 x 为矩形外接圆直径长时就可移转过去；结果取 n14 丙：如图 4，思路是当 x 为矩形的长与宽之和的倍时就可移转过去；结果取 n13 下列正确的是（ ） 11 A甲的思路错，他的 n 值对 B乙的思路和他的 n 值都对 C甲和丙的 n 值都对 D甲、乙的思路都错，而丙的思路对 【答案】B 【解答】解：甲的思路正确，长方形对角线最长，只要对角线能通过就可以，但是计算错误，应为 n14； 乙的思路与计算都正确； 乙的思路与计算都错误，图示情况不是最长； 5. (2019湖南益阳4 分)在如图所示的方格纸(1 格长为 1 个单位长度)中， ABC 的顶点都在格点上， 将ABC
17、 绕点 O 按顺时针方向旋转得到ABC，使各顶点仍在格点上，则其旋转角的度数是 【答案】90 【解答】解：根据旋转角的概念：对应点与旋转中心连线的夹角，可知BOB是旋转角，且BOB90 ， 故答案为 90 7. （2019海南省4 分）如图，将 RtABC 的斜边 AB 绕点 A 顺时针旋转 （0 90 ）得到 AE，直角 边 AC 绕点 A 逆时针旋转 （0 90 ）得到 AF，连结 EF若 AB3，AC2，且 +B，则 EF 【答案】 【解答】解：由旋转的性质可得 AEAB3，ACAF2， 12 B+BAC90 ，且 +B， BAC+90 EAF90 EF 故答案为： 8. (2019湖南
18、常德3 分)如图， 已知ABC 是等腰三角形， ABAC， BAC45 ， 点 D 在 AC 边上， 将ABD 绕点 A 逆时针旋转 45 得到ACD，且点 D、D、B 三点在同一条直线上，则ABD 的度数是 【答案】22.5 【解答】解：将ABD 绕点 A 逆时针旋转 45 得到ACD， BACCAD45 ，ADAD，ADD67.5 ，DAB90 ， ABD22.5 故答案为 22.5 9. (2019， 山西， 3 分） 如图， 在ABC 中， BAC=90 ， AB=AC=10cm， 点 D 为ABC 内一点， BAD=15 ， AD=6cm，连接 BD，将ABD 绕点 A 逆时针方向旋
19、转，使 AB 与 AC 重合，点 D 的对应点 E，连接 DE， DE 交 AC 于点 F，则 CF 的长为 cm. 【解析】过点 A 作 AGDE 于点 G，由旋转可知：AD=AE，DAE=90 ，CAE=BAD=15 AED=45 ；在AEF 中：AFD=AED+CAE=60 在 RtADG 中：AG=DG=23 2 AD 在 RtAFG 中：622,6 3 FGAF AG GF 13 6210AFACCF 故答案为：6210 10. （2019四川省广安市8 分）在数学活动课上，王老师要求学生将图 1 所示的 3 3 正方形方格纸，剪掉 其中两个方格，使之成为轴对称图形规定：凡通过旋转能
20、重合的图形视为同一种图形，如图 2 的四幅图 就视为同一种设计方案（阴影部分为要剪掉部分） 请在图中画出 4 种不同的设计方案，将每种方案中要剪掉的两个方格涂黑（每个 3 3 的正方形方格画一种， 例图除外） 【答案】根据轴对称图形和旋转对称图形的概念作图即可得 【解答】解：如图所示 11. (2019江苏苏州8 分)如图，ABC中，点E在BC边上，AEAB，将线段AC绕点A旋转到AF的位 置，使得CAFBAE ，连接EF，EF与AC交于点G （1）求证：EFBC； （2）若65ABC，28ACB，求FGC的度数. 14 【解答】解： （1）CAFBAE BACEAF AEABACAF又， B
21、ACEAF SAS EFBC （2）65ABAEABC， 18065250BAE 50FAG BACEAF又 28FC 502878FGC 12. （2019浙江绍兴12 分）如图 1 是实验室中的一种摆动装置，BC 在地面上，支架 ABC 是底边为 BC 的 等腰直角三角形，摆动臂 AD 可绕点 A 旋转，摆动臂 DM 可绕点 D 旋转，AD30，DM10 （1）在旋转过程中， 当 A，D，M 三点在同一直线上时，求 AM 的长 当 A，D，M 三点为同一直角三角形的顶点时，求 AM 的长 （2）若摆动臂 AD 顺时针旋转 90 ，点 D 的位置由ABC 外的点 D1转到其内的点 D2处，连
22、结 D1D2，如图 2，此时AD2C135 ，CD260，求 BD2的长 【答案】 （1）AMAD+DM40，或 AMADDM20 15 202或 1010 （2）306 【解答】解： （1）AMAD+DM40，或 AMADDM20 显然MAD 不能为直角 当AMD 为直角时，AM2AD2DM2302102800， AM202或（202舍弃） 当ADM90 时，AM2AD2+DM2302+1021000， AM1010或（1010舍弃） 综上所述，满足条件的 AM 的值为 202或 1010 （2）如图 2 中，连接 CD 由题意：D1AD290 ，AD1AD230， AD2D145 ，D1D
23、2302， AD2C135 ， CD2D190 ， CD1306， BACA1AD290 ， BACCAD2D2AD1CAD2， BAD1CAD2， ABAC，AD2AD1， BAD2CAD1（SAS） ， BD2CD1306 13. （2019湖北十堰10 分）如图 1，ABC 中，CACB，ACB，D 为ABC 内一点，将CAD 绕点 C 按逆时针方向旋转角 得到CBE，点 A，D 的对应点分别为点 B，E，且 A，D，E 三点在同一直线上 （1）填空：CDE 180 2 （用含 的代数式表示） ； （2）如图 2，若 60 ，请补全图形，再过点 C 作 CFAE 于点 F，然后探究线段
24、CF，AE，BE 之间的数 量关系，并证明你的结论； 16 （3）若 90 ，AC52，且点 G 满足AGB90 ，BG6，直接写出点 C 到 AG 的距离 【答案】 （1）180 2 ； （2）AEBE+ 2 3 3 CF； （3）点 C 到 AG 的距离为 1 或 7 【解答】解： （1）将CAD 绕点 C 按逆时针方向旋转角 得到CBE ACDBCE，DCE CDCE CDE180 2 故答案为：180 2 （2）AEBE+ 2 3 3 CF 理由如下：如图， 将CAD 绕点 C 按逆时针方向旋转角 60 得到CBE ACDBCE ADBE，CDCE，DCE60 CDE 是等边三角形，且 CFDE DFEF 3 3 CF AEAD+DF+EF 17 AEBE+ 2 3 3 CF （3）如图，当点 G 在 AB 上方时，过点 C 作 CEAG 于点 E， ACB90 ，ACBC52， CABABC45 ，AB10 ACB90 AGB 点 C，点 G，点 B，点 A 四点共圆 AGCABC45 ，且 CEAG AGCECG45 CEGE AB10，GB6，AGB90 AG8 AC2AE2+CE2， （52）2（8CE）2+CE2， CE7（不合题意舍去） ，CE1 若点 G 在 AB 的下方，过点 C 作 CFAG， 同理可得：CF7 点 C 到 AG 的距离为 1 或 7
