1、浙江省温州市三校浙江省温州市三校 2020-2021 学年八年级上学期数学期中考试试卷学年八年级上学期数学期中考试试卷 一、精心选一选（每小题一、精心选一选（每小题 3 分，共分，共 30 分）分） 1.以下列数据为长度的三条线段，能组成三角形的是（ ） A. 1，2，3 B. 6, 8, 15 C. 8 ,4, 3 D. 4, 6, 5 2.下列学习用具中，其形状不是轴对称图形的是（ ） A. B. C. D. 3.如图， ACBA1CB1, AB=2，AC=3，BC=4，则 A1 C 的长为（ ） A. 2 B. 3 C. 4 D. 2.5 4.下列语句是命题的是（ ） A. 等腰三角形是
2、轴对称图形 B. 将 27 开立方 C. 画一个角等于已知角 D. 垂线段最短吗? 5.若等腰三角形的两边长分别为 4 和 9，则它的周长为（ ） A. 13 B. 17 C. 22 D. 17 或 22 6.如果直角三角形的两条直角边的长分别为 6cm 和 8cm，那么斜边上的中线等于（ ） A. 2.4cm B. 4.8cm C. 5cm D. 10cm 7.已知 AD 是 ABC 的中线，BE 是 ABD 的中线，若 ACD 的面积为 20，则 ABE 的面积为（ ） A. 5 B. 10 C. 15 D. 18 8.下列条件中，不能判断一个三角形是直角三角形的是（ ） A. 三条边的比
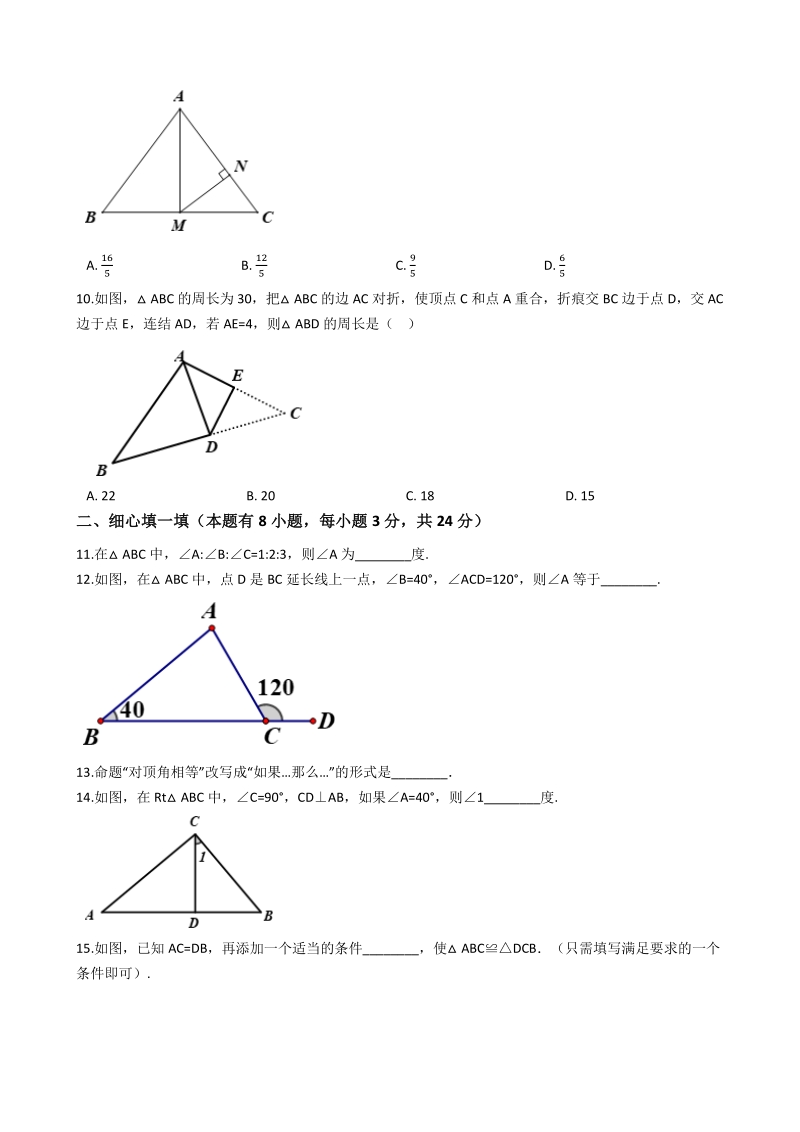
3、是 123 B. 三条边满足关系 a2=c2b2 C. 三个角的比是 123 D. 三个角满足关系B+C=A 9.如图，在 ABC 中，AB=AC=5，BC=6，点 M 为 BC 的中点，MNAC 于点 N，则 MN 等于（ ） A. B. C. D. 10.如图， ABC 的周长为 30，把 ABC 的边 AC 对折，使顶点 C 和点 A 重合，折痕交 BC 边于点 D，交 AC 边于点 E，连结 AD，若 AE=4，则 ABD 的周长是（ ） A. 22 B. 20 C. 18 D. 15 二、细心填一填（本题有二、细心填一填（本题有 8 小题，每小题小题，每小题 3 分，共分，共 24
4、分）分） 11.在 ABC 中，A:B:C=1:2:3，则A 为_度. 12.如图，在 ABC 中，点 D 是 BC 延长线上一点，B=40，ACD=120，则A 等于_. 13.命题“对顶角相等”改写成“如果那么”的形式是_ 14.如图，在 Rt ABC 中，C=90，CDAB，如果A=40，则1_度. 15.如图，已知 AC=DB，再添加一个适当的条件_，使 ABCDCB（只需填写满足要求的一个 条件即可）. 16.如图， ABC 中，AB=AC，BC=3，点 E 为中线 AD 上一点，已知 ABE 和 CDE 的面积分别为 1.5 和 2， 则 AD 的长度为 _. 17.如图，已知 A
5、BD， BCE 均为等腰直角三角形，若 CD=8，BE=3，则 AC 等于_ . 18.如图 1 是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成若较短的直角边 BC=2.5，将四个直角三角形中较长的直角边分别向外延长一倍，得到图 2 所示的“数学风车”，若 BCD 的 周长是 15，则这个风车的外围周长 是_ 三、动脑想一想（本题有三、动脑想一想（本题有 6 小题，共小题，共 46 分）分） 19.如图，点 B、E、C、F 在一条直线上，B=DEF，AB=DE，BE=CF，F=700 ， 求ACB 的度数. 20.如图，在 ABC 中，AB=AC,D 为 BC 边上中点，
6、DMAC 于点 M，, DNAB 于点 N.求证：DM=DN. 21.已知：如图，A,B,D 在同一条直线上，1=2，A=D=Rt，AC=BD. （1） ABC 与 DEB 全等吗？请说明理由; （2）求证： CBE 为等腰直角三角形. 22.在如图所示的网格中，每个小正方形的边长均为 1 个单位。 （1）请你在图 1 中画一个以格点为顶点，面积为 6 个平方单位的等腰三角形。 （2）请你在图 2 中画一条以格点为端点，长度为 的线段. （3）请你在图 3 中画一个以格点为顶点， 为直角边的直角三角形。 23.如图，在等边 ABC 中，D、E 分别在边 BC、AC 上，且 DEAB，过点 E
7、作 EFDE 交 BC 的延长线于点 F. （1）求F 的度数 （2）若 CD=2cm，求 DF 的长 24.如图， ABC 中， BE 平分ABC 交 AC 边于点 E，过点 E 作 DEBC 交 AB 于点 D， （1）求证： BDE 为等腰三角形; （2）若点 D 为 AB 中点，AB=6，求线段 BC 的长; （3）在（2）条件下，若BAC=60，动点 P 从点 B 出发，以每秒 1 个单位的速度沿射线 BE 运动，请直接 写出当 ABP 为等腰三角形时 t 的值. 答案解析答案解析 一、精心选一选（每小题 3 分，共 30 分） 1.【答案】 D 【考点】三角形三边关系 【解析】【解
8、答】解：A、1+2=3，故不能构成三角形，A 不符合题意； B、6+815，故不能构成三角形，B 不符合题意； C、3+48，故不能构成三角形，C 不符合题意； D、4+56，故能构成三角形，D 符合题意； 故答案为：D. 【分析】三角形三边关系：两边之和大于第三边 ，两边之差小于第三边，依此逐一分析即可得出答案. 2.【答案】 C 【考点】轴对称图形 【解析】【解答】解：A、是轴对称图形，A 不符合题意； B、是轴对称图形，B 不符合题意； C、不是轴对称图形，C 符合题意； D、是轴对称图形，D 不符合题意； 故答案为：C. 【分析】轴对称图形：一个图形沿一条直线折叠，直线两旁的部分能够完
9、全重合的图形，依此逐一分析 即可得出答案. 3.【答案】 B 【考点】三角形全等及其性质 【解析】【解答】解：ACBA1CB1 ， AC=A1C， 又AC=3， A1C=3. 故答案为：B. 【分析】根据全等三角形的性质：全等三角形的对应边相等，依此即可得出答案. 4.【答案】 A 【考点】定义、命题及定理的概念 【解析】【解答】解：A、等腰三角形是轴对称图形，是命题，A 符合题意； B、将 27 开立方，是描述性语言，不是命题，B 不符合题意； C、画一个角等于已知角，是描述性语言，不是命题，C 不符合题意； D、垂线段最短吗？是疑问句，不是命题，D 不符合题意； 故答案为：A. 【分析】命
10、题：用语言、符号或式子表达的，可以判断真假的陈述句；依此逐一分析即可得出答案. 5.【答案】 C 【考点】等腰三角形的性质 【解析】【解答】解：等腰三角形的两边长分别为 4 和 9， 底边长为 4，腰长为 9， 它的周长为：4+9+9=22. 故答案为：C. 【分析】根据三角形的两边之和大于第三边得出等腰三角形的底边长和腰长，由三角形周长概念即可得 出答案. 6.【答案】 C 【考点】直角三角形的性质 【解析】【解答】解：直角三角形的两条直角边的长分别为 6cm 和 8cm， 斜边长为： =10（cm）， 斜边上的中线长为： 10=5（cm）. 故答案为：C. 【分析】根据勾股定理求得斜边长，
11、再由直角三角形中，斜边上的中线等于斜边的一半，从而得出答案. 7.【答案】 B 【考点】三角形的面积 【解析】【解答】解：S ACD=20，AD 是 ABC 的中线， S ABD=S ACD=20， 又BE 是 ABD 的中线， S ABE= S ABD= 20=10， 故答案为：B. 【分析】根据中线的性质可得 S ABD=S ACD=20，再由 BE 是中线得 S ABE= S ABD ， 计算可得答案. 8.【答案】 A 【考点】三角形内角和定理，勾股定理的逆定理 【解析】【解答】解：A、三条边的比是 1：2：3， 设三边依次是 a，2a，3a， a2+（2a）2=5a2（3a）2 ，
12、此三角形不是直角三角形，A 符合题意； B、三条边满足关系 a2=c2-b2 ， a2+b2=c2 ， 此三角形是直角三角形，B 不符合题意； C、三个角的比是 1：2：3， 三个角依次是：30，60，90， 此三角形是直角三角形，C 不符合题意； D、三个角满足关系B+C=A， A=90， 此三角形是直角三角形，D 不符合题意； 故答案为：A. 【分析】A、由已知条件可知两边的平方和不等于第三边，不满足勾股定理逆定理，故不是直角三角形； B、三边关系满足勾股定理逆定理，故是直角三角形；C、由已知条件求得三个角的度数，由直角三角形定 义可得是直角三角形；D、由三角形内角和定理求得A=90，由直
13、角三角形定义可得是直角三角形. 9.【答案】 B 【考点】三角形的面积，等腰三角形的性质 【解析】【解答】解：BC=6，点 M 为 BC 的中点， BM=CM=3， AB=AC=5，点 M 为 BC 的中点， AMBC， 在 Rt AMC 中， AM= =4， MNAC， S ACM= AMCM= ACMN， 即 43=5MN， MN= . 故答案为：B. 【分析】根据等腰三角形三线合一的性质可得 AMBC，在 Rt AMC 中，由勾股定理求得 AM=4，由等面 积法可求得 MN 长. 10.【答案】 A 【考点】翻折变换（折叠问题） 【解析】【解答】解：依题可得， AE=CE=4，CD=AD
14、， AC=8， C ABC=AB+BC+CA=30， AB+BC=30-8=22， C ABD=AB+BD+DA=AB+BD+CD=AB+BC=22. 故答案为：A. 【分析】根据折叠的性质得 AE=CE=4，CD=AD，再由三角形周长结合已知条件即可求得答案. 二、细心填一填（本题有 8 小题，每小题 3 分，共 24 分） 11.【答案】 30 【考点】三角形内角和定理 【解析】【解答】解：A：B：C=1：2：3， A=180 =30. 故答案为：30. 【分析】根据三角形各角之间的关系结合三角形内角和定理即可求得答案. 12.【答案】 80 【考点】三角形的外角性质 【解析】【解答】解：
15、ACD=B+A，B=40，ACD=120， A=120-40=80. 故答案为：80. 【分析】由三角形外角和定理：三角形一个外角等于与它不相邻的两个内角和，依此计算即可得出答案. 13.【答案】 如果两个角是对顶角，那么这两个角相等 【考点】定义、命题及定理的概念 【解析】【解答】解：依题可得， 如果两个角是对顶角，那么这两个角相等. 故答案为：如果两个角是对顶角，那么这两个角相等. 【分析】找出命题的条件和结论即可得出答案. 14.【答案】 40 【考点】三角形内角和定理 【解析】【解答】解：在 Rt ABC 中， C=90，A=40， B=50， 又CDAB， CDB=90， 1=40.
16、 故答案为：40. 【分析】在 Rt ABC 中，根据三角形内角和定理求得B 度数，在 Rt CDB 中，根据三角形内角和定理即 可求得答案. 15.【答案】 AB=CD 【考点】三角形全等的判定 【解析】【解答】AC=DB，BC=BC，AB=DC ABCDCB 加一个适当的条件是 AB=DC. 【分析】根据三角形全等的判定方法，要使 ABCDCB，已知两边对应相等再添加一组对应边相等，可 根据边边边判定其全等 。（添加这两边的夹角也可以判定其全等）。 16.【答案】 【考点】三角形的面积 【解析】【解答】解：AB=AC，D 是边 BC 上的中点，BC=3， ADBC，BD=CD= ， 又S
17、ABE= BDAE= AE=1.5， S CDE= CDDE= DE=2， AE=2，DE= ， AD=AE+DE=2+ = . 故答案为： . 【分析】 根据等腰三角形三线合一的性质得ADBC， BD=CD= ， 根据三角形的面积公式分别求得AE=2， DE= ， 由 AD=AE+DE 即可求得答案. 17.【答案】 【考点】等腰直角三角形 【解析】【解答】解： ABD， BCE 均为等腰直角三角形， DB=AB，CB=EB， 又CD=8，BE=3， BC=BE=3，DB=AB=CD-BC=5， 在 Rt ABC 中， AC= = . 故答案为： . 【分析】 根据等腰直角三角形性质结合已知
18、条件得 BC=BE=3，DB=AB=5，在 Rt ABC 中，由勾股定理求得 AC 长. 18.【答案】 38 【考点】勾股定理的应用 【解析】【解答】解：设图 2 中的“数学风车”四个直角三角形的斜边长为 x，AC=y，依题可得， ( ) ) ， 解得： ) ， 这个风车的外围周长为：46.5+43=38. 故答案为：38. 【分析】根据勾股定理和三角形的周长列出方程组，解之求得“数学风车”四个直角三角形的斜边长和 AC 长，再由周长公式求得答案. 三、动脑想一想（本题有 6 小题，共 46 分） 19.【答案】 解：BE=CF BE+EC=CF+EC 即 BC=EF AB=DE,B=DEF
19、 ABCDEF(SAS) ACB=F=70 【考点】三角形全等及其性质 【解析】【分析】根据等量代换结合已知条件得 BC=EF，由全等三角形的判定 SAS 得 ABCDEF，再根 据全等三角形的性质即可求得 ACB 度数. 20.【答案】 证明：AB=AC D 为 BC 中点 AD 平分BAC DMAC DNAB DM=DN 【考点】角平分线的性质 【解析】【分析】根据等腰三角形三线合一的性质可得 AD 平分BAC，再由角平分线性质得证. 21.【答案】 （1）解：全等，理由如下： 1=2 BC=BE A=D=90，AC=BD Rt ABCRt DEB(HL) （2）证明：Rt ABCRt D
20、EB ABC=DEB DEB+EBD=90 ABC+EBD=90 CBE=90 BC=BE CBE 为等腰直角三角形 【考点】直角三角形全等的判定（HL），等腰直角三角形 【解析】 【分析】 （1）由根据等腰三角形性质：等角对等边求得 BC=BE ，再根据直角三角形的判定HL 即可得证. （2）根据全等三角形性质：全等三角形的对应角相等得ABC=DEB，由三角形内角和、等量代换可得 CBE=90，由 BC=BE 即可得证. 22.【答案】 （1）解：如图 1 所示 （2）解：如图 2 所示 （3）解：如图 3 所示。 【考点】等腰三角形的性质，勾股定理 【解析】【分析】（1）开放性的命题，答案
21、不唯一，根据格点三角形的定义，由三角形的面积计算方法， 三角形的面积等于 6，则该三角形的底为 6，高为 2；底为 4，高为 3；底为 2，高为 6，再格努等腰三角形 的性质即可画出图形； （2）根据勾股定理， 是直角边为 1,2 的直角三角形的斜边，利用方格纸的特点即可作出图形； （3）开放性的命题，答案不唯一，根据勾股定理， 是直角边为 1,2 的直角三角形的斜边，以 为直角 边，利用方格纸的特点及直角三角形的性质即可作出图形。 23.【答案】 （1）解：ABC 是等边三角形， B=60， DEAB， EDC=B=60 EFDE， DEF=90， F=90EDC=30 （2）解：ACB=6
22、0，EDC=60， EDC 是等边三角形ED=DC=2， DEF=90，F=30 DF=2DE=4 【考点】等边三角形的判定与性质，含 30 度角的直角三角形 【解析】【分析】（1） 根据等边三角形的性质得出B=60， 根据二直线平行同位角相等得出EDC=B=60， 根据垂直的定义及三角形的内角和即可算出F 的度数； （2）由有两个角是 60的三角形是等边三角形得出 EDC 是等边三角形，根据等边三角形的三边相等得出 ED=DC=2，根据含 30直角三角形的边之间的关系即可得出 DF=2DE=4。 24.【答案】 （1）证明：BE 平分ABC ABE=EBC DEBC DEB=EBC DEB=
23、ABE BD=ED DBE 为等腰三角形 （2）解：点 D 为 AB 中点 AD=BD=ED A=AED A+AED+ABE+BED=180 AED+BED=90 即AEB=90=CEB ABE=EBC BE=BE ABECBE(ASA) BC=AB=6 （3）解：6， ， 【考点】三角形全等及其性质，等腰三角形的判定，三角形的综合，三角形-动点问题 【解析】【解答】解：（3）由（2）可知 BC=AB=6， BAC=60， ABC 为等边三角形， 由（2）知 BEAC， AE=3，BE= =3 ， ABP 为等腰三角形， 当 AB=BP=6 时， 点 P 的运动速度每秒 1 个单位， t=6；
24、 当 AB=AP=6 时， BP=2BE=23 =6 ； t=6 ； 当 AP=BP 时， 过点 P 作 PFAB 交 AB 于点 F，如图： BF= AB=3， 在 Rt PBF 中， PBF= ABC=30， BP=2PF， BP2-PF2=BF2=9， PF= ， BP=2 ， t=2 ； 综上所述：t 值为 6，6 ， 2 . 【分析】 （1） 由角平分线得ABE=EBC， 根据平行线性质： 两直线平行， 内错角相等得 DEB=EBC ， 再由等量代换得 DEB=ABE， 根据等腰三角形性质： 等角对等边得 BD=ED， 结合等腰三角形定义即得证. （2）由等腰三角形性质和三角形内角和定理得 AED+BED=90，再由全等三角形判定ASA 得 ABECBE ，根据全等三角形性质：全等三角形对应边相等即可得证. （3）由（2）以及等边三角形的定义可知 ABC 为等边三角形，根据勾股定理求得 BE=3 ， 分三种 情况讨论：当 AB=BP=6 时，当 AB=AP=6 时，当 AP=BP 时，结合已知条件求得各自答案.
