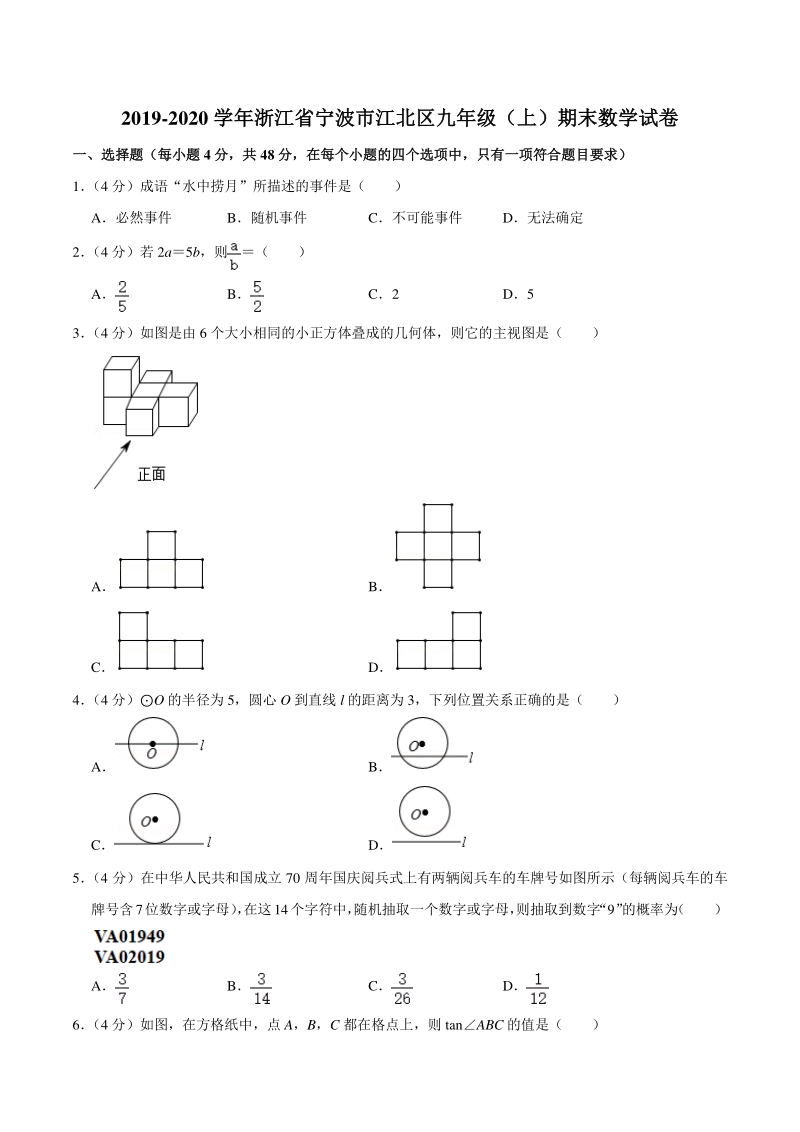
1、2019-2020 学年浙江省宁波市江北区九年级（上）期末数学试卷学年浙江省宁波市江北区九年级（上）期末数学试卷 一、选择题（每小题一、选择题（每小题 4 分，共分，共 48 分，在每个小题的四个选项中，只有一项符合题目要求）分，在每个小题的四个选项中，只有一项符合题目要求） 1 （4 分）成语“水中捞月”所描述的事件是（ ） A必然事件 B随机事件 C不可能事件 D无法确定 2 （4 分）若 2a5b，则（ ） A B C2 D5 3 （4 分）如图是由 6 个大小相同的小正方体叠成的几何体，则它的主视图是（ ） A B C D 4 （4 分）O 的半径为 5，圆心 O 到直线 l 的距离为
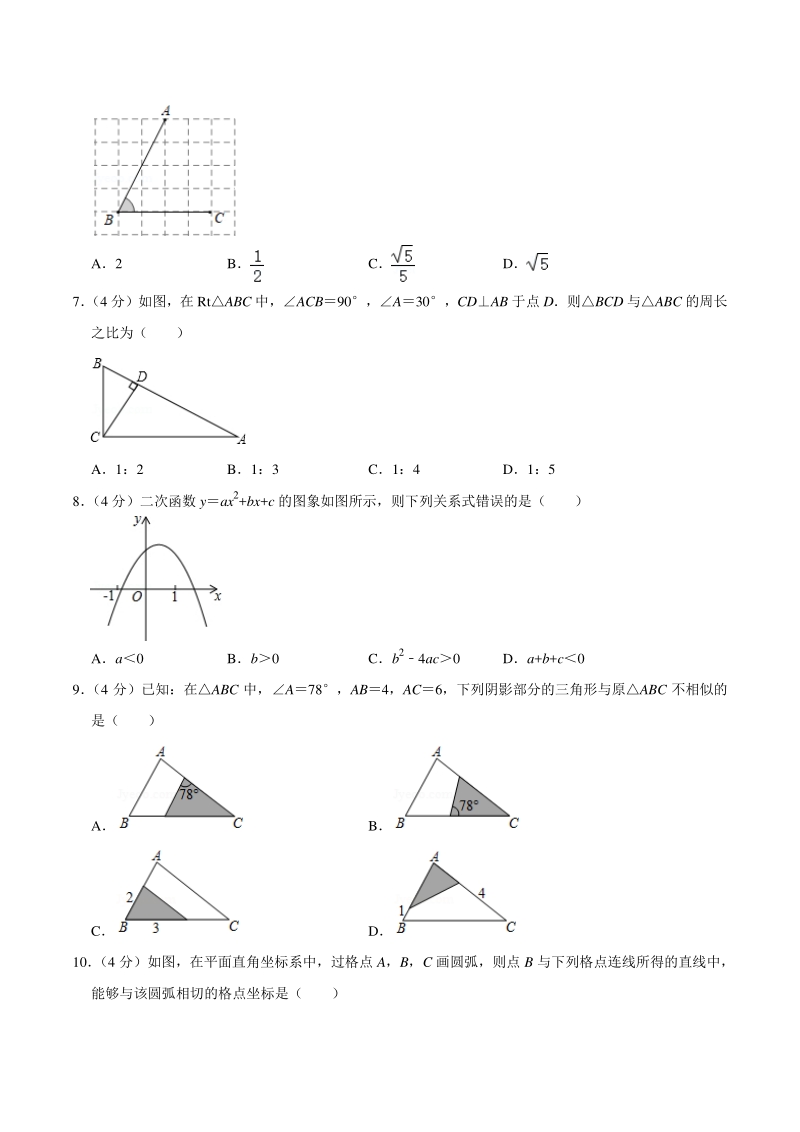
2、 3，下列位置关系正确的是（ ） A B C D 5 （4 分）在中华人民共和国成立 70 周年国庆阅兵式上有两辆阅兵车的车牌号如图所示（每辆阅兵车的车 牌号含7位数字或字母） ， 在这14个字符中， 随机抽取一个数字或字母， 则抽取到数字 “9” 的概率为 （ ） A B C D 6 （4 分）如图，在方格纸中，点 A，B，C 都在格点上，则 tanABC 的值是（ ） A2 B C D 7 （4 分）如图，在 RtABC 中，ACB90，A30，CDAB 于点 D则BCD 与ABC 的周长 之比为（ ） A1：2 B1：3 C1：4 D1：5 8 （4 分）二次函数 yax2+bx+c 的
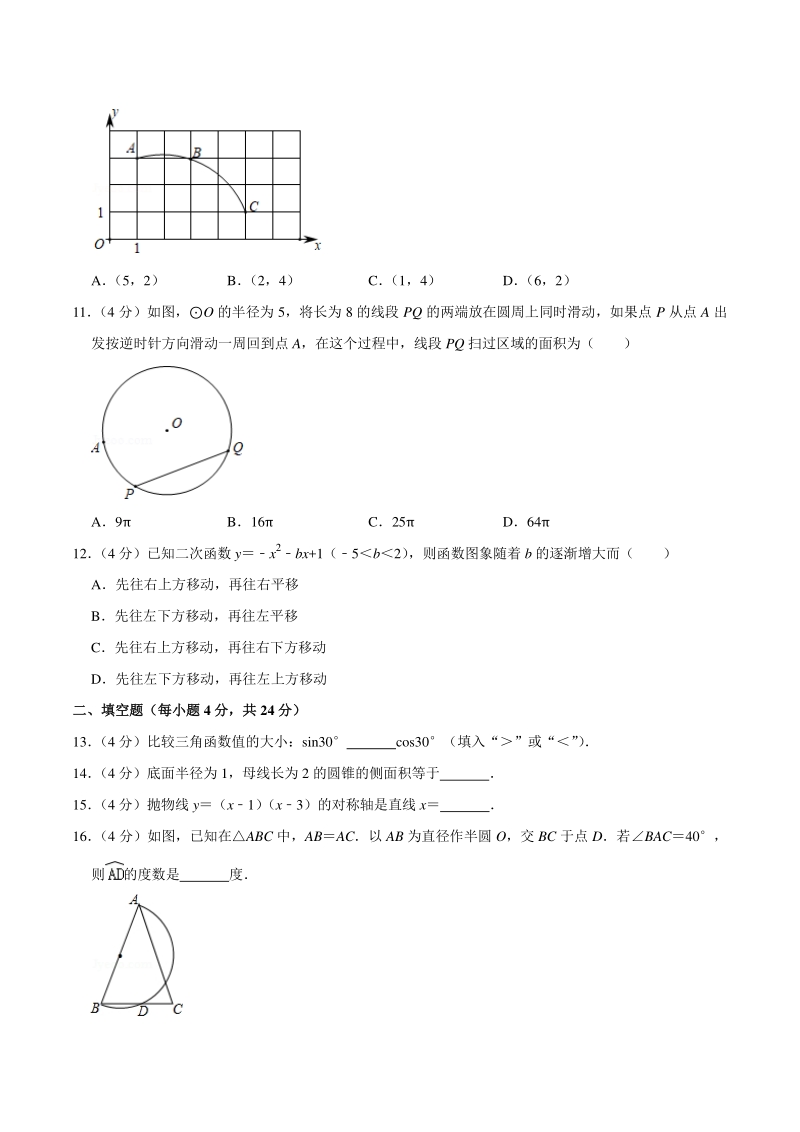
3、图象如图所示，则下列关系式错误的是（ ） Aa0 Bb0 Cb24ac0 Da+b+c0 9 （4 分）已知：在ABC 中，A78，AB4，AC6，下列阴影部分的三角形与原ABC 不相似的 是（ ） A B C D 10 （4 分）如图，在平面直角坐标系中，过格点 A，B，C 画圆弧，则点 B 与下列格点连线所得的直线中， 能够与该圆弧相切的格点坐标是（ ） A （5，2） B （2，4） C （1，4） D （6，2） 11 （4 分）如图，O 的半径为 5，将长为 8 的线段 PQ 的两端放在圆周上同时滑动，如果点 P 从点 A 出 发按逆时针方向滑动一周回到点 A，在这个过程中，线段 P
4、Q 扫过区域的面积为（ ） A9 B16 C25 D64 12 （4 分）已知二次函数 yx2bx+1（5b2） ，则函数图象随着 b 的逐渐增大而（ ） A先往右上方移动，再往右平移 B先往左下方移动，再往左平移 C先往右上方移动，再往右下方移动 D先往左下方移动，再往左上方移动 二、填空题（每小题二、填空题（每小题 4 分，共分，共 24 分）分） 13 （4 分）比较三角函数值的大小：sin30 cos30（填入“”或“” ） 14 （4 分）底面半径为 1，母线长为 2 的圆锥的侧面积等于 15 （4 分）抛物线 y（x1） （x3）的对称轴是直线 x 16 （4 分）如图，已知在AB
5、C 中，ABAC以 AB 为直径作半圆 O，交 BC 于点 D若BAC40， 则的度数是 度 17 （4 分）如图，在ABC 中，D、E、F 分别在 AB、AC、BC 上，DEBC，EFAB，AD：BD5：3， CF6，则 DE 的长为 18 （4 分）如图，已知O 的半径为 2，弦 AB2，点 P 为优弧上动点，点 I 为PAB 的内心，当 点 P 从点 A 向点 B 运动时，点 I 移动的路径长为 三、解答题（本大题有三、解答题（本大题有 8 小题，第小题，第 19 题题 6 分，第分，第 20，21，22 题各题各 8 分，第分，第 23 题题 10 分，第分，第 24 题题 12 分，
6、分， 第第 25 题题 12 分，第分，第 26 题题 14 分，共分，共 78 分）分） 19 （6 分）计算：|+202002sin30+ 20 （8 分）我区某中学举行了“垃圾分类，绿色环保”知识竞赛活动，根据学生的成绩划分为 A，B，C， D 四个等级，并绘制了不完整的两种统计图： 根据图中提供的信息，回答下列问题： （1）参加知识竞赛的学生共有 人，并把条形统计图补充完整； （2）扇形统计图中，m ，n ，C 等级对应的圆心角为 度； （3）小明是四名获 A 等级的学生中的一位，学校将从获 A 等级的学生中任选取 2 人，参加区举办的知 识竞赛，请用列表法或画树状图，求小明被选中参加
7、区知识竞赛的概率 21 （8 分）已知二次函数 yx22x3 （1）求函数图象的顶点坐标，与坐标轴的交点坐标，并画出函数的大致图象； （2）根据图象直接回答：当 y0 时，求 x 的取值范围；当 y3 时，求 x 的取值范围 22 （8 分）如图，某航天飞机在地球表面点 P 的正上方 A 处，从 A 处观测到地球上的最远点 Q，即 AQ 是 O 的切线，若QAP，地球半径为 R， 求： （1）航天飞机距地球表面的最近距离 AP 的长； （2）P、Q 两点间的地面距离，即的长 （注：本题最后结果均用含 ，R 的代数式表示） 23 （10 分）如图，直线 MN 交O 于 A，B 两点，AC 是O
8、直径，CAM 的平分线交O 于点 D，过点 D 作 DEMN 于点 E （1）求证：DE 是O 的切线； （2）若 DE6cm，AE3cm，求O 的半径 24 （12 分） （1）如图 1，在平行四边形 ABCD 中，点 E1，E2是 AB 三等分点，点 F1，F2是 CD 三等分点， E1F1，E2F2分别交 AC 于点 G1，G2，求证：AG1G1G2G2C （2）如图 2，由 64 个边长为 1 的小正方形组成的一个网格图，线段 MN 的两个端点在格点上，请用一 把无刻度的尺子，画出线段 MN 三等分点 P，Q （保留作图痕迹） 25（12 分） 每年十月的第二个周四是世界爱眼日， 为预
9、防近视， 超市决定对某型号护眼台灯进行降价销售 降 价前，进价为 30 元的护眼台灯以 80 元售出，平均每月能售出 200 盏，调查表明：这种护眼台灯每盏售 价每降低 1 元，其月平均销售量将增加 10 盏 （1）写出月销售利润 y（单位：元）与销售价 x（单位：元/盏）之间的函数表达式； （2）当销售价定为多少元时，所得月利润最大？最大月利润为多少元？ 26 （14 分）问题提出： 如图 1，在等边ABC 中，AB9，C 半径为 3，P 为圆上一动点，连结 AP，BP，求 AP+BP 的最小 值 （1）尝试解决： 为了解决这个问题，下面给出一种解题思路，通过构造一对相似三角形，将BP 转化
10、为某一条线段长， 具体方法如下： （请把下面的过程填写完整） 如图 2，连结 CP，在 CB 上取点 D，使 CD1，则有 又PCD PDBP AP+BPAP+PD 当 A，P，D 三点共线时，AP+PD 取到最小值 请你完成余下的思考，并直接写出答案：AP+BP 的最小值为 （2）自主探索： 如图 3， 矩形 ABCD 中， BC6， AB8， P 为矩形内部一点， 且 PB4， 则AP+PC 的最小值为 （请 在图 3 中添加相应的辅助线） （3）拓展延伸： 如图 4，在扇形 COD 中，O 为圆心，COD120，OC4OA2，OB3，点 P 是上一点，求 2PA+PB 的最小值，画出示意
11、图并写出求解过程 2019-2020 学年浙江省宁波市江北区九年级（上）期末数学试卷学年浙江省宁波市江北区九年级（上）期末数学试卷 参考答案与试题解析参考答案与试题解析 一、选择题（每小题一、选择题（每小题 4 分，共分，共 48 分，在每个小题的四个选项中，只有一项符合题目要求）分，在每个小题的四个选项中，只有一项符合题目要求） 1 （4 分）成语“水中捞月”所描述的事件是（ ） A必然事件 B随机事件 C不可能事件 D无法确定 【分析】根据必然事件、不可能事件、随机事件的概念进行解答即可 【解答】解：水中捞月是不可能事件， 故选：C 【点评】本题考查的是必然事件、不可能事件、随机事件的概念
12、必然事件指在一定条件下，一定发生 的事件 不可能事件是指在一定条件下， 一定不发生的事件， 不确定事件即随机事件是指在一定条件下， 可能发生也可能不发生的事件 2 （4 分）若 2a5b，则（ ） A B C2 D5 【分析】根据等式的性质，可得答案 【解答】解：两边都除以 2b，得 ， 故选：B 【点评】本题考查了比例的性质，利用等式的性质是解题关键 3 （4 分）如图是由 6 个大小相同的小正方体叠成的几何体，则它的主视图是（ ） A B C D 【分析】找到从正面看所得到的图形即可 【解答】解：它的主视图是： 故选：C 【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图 4
13、 （4 分）O 的半径为 5，圆心 O 到直线 l 的距离为 3，下列位置关系正确的是（ ） A B C D 【分析】根据圆 O 的半径和圆心 O 到直线 l 的距离的大小，相交：dr；相切：dr；相离：dr；即 可选出答案 【解答】解：O 的半径为 5，圆心 O 到直线 l 的距离为 3， 53，即：dr， 直线 L 与O 的位置关系是相交 故选：B 【点评】本题主要考查对直线与圆的位置关系的性质的理解和掌握，能熟练地运用性质进行判断是解此 题的关键 5 （4 分）在中华人民共和国成立 70 周年国庆阅兵式上有两辆阅兵车的车牌号如图所示（每辆阅兵车的车 牌号含7位数字或字母） ， 在这14个
14、字符中， 随机抽取一个数字或字母， 则抽取到数字 “9” 的概率为 （ ） A B C D 【分析】直接利用概率公式计算得出答案 【解答】解：由题意可得：9 出现 3 次，故在这 14 个字符中，随机抽取一个数字或字母， 则抽取到数字“9”的概率为： 故选：B 【点评】此题主要考查了概率公式，正确掌握概率求法是解题关键 6 （4 分）如图，在方格纸中，点 A，B，C 都在格点上，则 tanABC 的值是（ ） A2 B C D 【分析】根据直角三角形解决问题即可 【解答】解：作 AEBCAEC90，AE4，BE2， tanABC2， 故选：A 【点评】本题考查解直角三角形，解题的关键是学会添加
15、常用辅助线，构造直角三角形解决问题 7 （4 分）如图，在 RtABC 中，ACB90，A30，CDAB 于点 D则BCD 与ABC 的周长 之比为（ ） A1：2 B1：3 C1：4 D1：5 【分析】易证得BCDBAC，得BCDA30，那么 BC2BD，即BCD 与BAC 的相似比 为 1：2，根据相似三角形的周长比等于相似比即可得到正确的结论 【解答】解：BB，BDCBCA90， BCDBAC； BCDA30； RtBCD 中，BCD30，则 BC2BD； 由得：CBCD：CBACBD：BC1：2； 故选：A 【点评】此题主要考查的是直角三角形和相似三角形的性质； 相似三角形的性质：相似
16、三角形的周长比等于相似比，面积比等于相似比的平方 8 （4 分）二次函数 yax2+bx+c 的图象如图所示，则下列关系式错误的是（ ） Aa0 Bb0 Cb24ac0 Da+b+c0 【分析】根据抛物线的开口方向对 A 进行判断；根据抛物线的对称轴位置对 B 进行判断；根据抛物线与 x 轴的交点个数对 C 进行判断；根据自变量为 1 所对应的函数值为正数对 D 进行判断 【解答】解：A、抛物线开口向下，则 a0，所以 A 选项的关系式正确； B、抛物线的对称轴在 y 轴的右侧，a、b 异号，则 b0，所以 B 选项的关系式正确； C、抛物线与 x 轴有 2 个交点，则b24ac0，所以 D
17、选项的关系式正确； D、当 x1 时，y0，则 a+b+c0，所以 D 选项的关系式错误 故选：D 【点评】本题考查了二次函数图象与系数的关系：对于二次函数 yax2+bx+c（a0） ，二次项系数 a 决 定抛物线的开口方向和大小，当 a0 时，抛物线向上开口；当 a0 时，抛物线向下开口；一次项系数 b 和二次项系数 a 共同决定对称轴的位置：当 a 与 b 同号时（即 ab0） ，对称轴在 y 轴左； 当 a 与 b 异 号时（即 ab0） ，对称轴在 y 轴右 （简称：左同右异） ；常数项 c 决定抛物线与 y 轴交点：抛物线与 y 轴交于（0，c） 抛物线与 x 轴交点个数由决定：b
18、24ac0 时，抛物线与 x 轴有 2 个交点； b24ac0 时，抛物线与 x 轴有 1 个交点；b24ac0 时，抛物线与 x 轴没有交点 9 （4 分）已知：在ABC 中，A78，AB4，AC6，下列阴影部分的三角形与原ABC 不相似的 是（ ） A B C D 【分析】根据相似三角形的判定定理对各选项进行逐一判定即可 【解答】解：A、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项不符合题意； B、阴影部分的三角形与原三角形有两个角相等，故两三角形相似，故本选项不符合题意； C、两三角形的对应边不成比例，故两三角形不相似，故本选项符合题意 D、两三角形对应边成比例且夹角
19、相等，故两三角形相似，故本选项不符合题意； 故选：C 【点评】本题考查的是相似三角形的判定，熟知相似三角形的判定定理是解答此题的关键 10 （4 分）如图，在平面直角坐标系中，过格点 A，B，C 画圆弧，则点 B 与下列格点连线所得的直线中， 能够与该圆弧相切的格点坐标是（ ） A （5，2） B （2，4） C （1，4） D （6，2） 【分析】根据切线的判定在网格中作图即可得结论 【解答】解：如图， 过格点 A，B，C 画圆弧，则点 B 与下列格点连线所得的直线中， 能够与该圆弧相切的格点坐标是（6，2） 故选：D 【点评】本题考查了切线的判定，解决本题的关键是掌握切线的判定定理 11
20、（4 分）如图，O 的半径为 5，将长为 8 的线段 PQ 的两端放在圆周上同时滑动，如果点 P 从点 A 出 发按逆时针方向滑动一周回到点 A，在这个过程中，线段 PQ 扫过区域的面积为（ ） A9 B16 C25 D64 【分析】如图，线段 PQ 扫过的面积是图中圆环面积作 OEPQ 于 E，连接 OQ 求出 OE 即可解决问 题 【解答】解：如图，线段 PQ 扫过的面积是图中圆环面积 作 OEPQ 于 E，连接 OQ OEPQ， EQPQ4， OQ5， OE3， 线段 PQ 扫过区域的面积523216， 故选：B 【点评】本题考查轨迹，解直角三角形，垂径定理等知识，解题的关键是理解题意，
21、学会添加常用辅助 线，属于中考常考题型 12 （4 分）已知二次函数 yx2bx+1（5b2） ，则函数图象随着 b 的逐渐增大而（ ） A先往右上方移动，再往右平移 B先往左下方移动，再往左平移 C先往右上方移动，再往右下方移动 D先往左下方移动，再往左上方移动 【分析】先分别求出当 b5、0、2 时函数图象的顶点坐标即可得结论 【解答】解：二次函数 yx2bx+1（5b2） ， 当 b5 时， yx2+5x+1 （x）2+ 顶点坐标为（，） ； 当 b0 时， yx2+1 顶点坐标为（0，1） ； 当 b2 时， yx22x+1 （x+1）2+2 顶点坐标为（1，2） 故函数图象随着 b
22、的逐渐增大而先往左下方移动，再往左上方移动 故选：D 【点评】本题考查了二次函数图象与几何变换、熟练掌握二次函数的性质是解决本题的关键 二、填空题（每小题二、填空题（每小题 4 分，共分，共 24 分）分） 13 （4 分）比较三角函数值的大小：sin30 cos30（填入“”或“” ） 【分析】直接利用特殊角的三角函数值分别代入比较得出答案 【解答】解：sin30，cos30 sin30cos30 故答案为： 【点评】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键 14 （4 分）底面半径为 1，母线长为 2 的圆锥的侧面积等于 2 【分析】根据圆锥的侧面积就等于母线长乘底面周
23、长的一半依此公式计算即可解决问题 【解答】解：圆锥的侧面积2222 故答案为：2 【点评】本题主要考查了圆锥的侧面积的计算公式熟练掌握圆锥侧面积公式是解题关键 15 （4 分）抛物线 y（x1） （x3）的对称轴是直线 x 2 【分析】将抛物线的解析式化为顶点式，即可得到该抛物线的对称轴，本题得以解决 【解答】解：抛物线 y（x1） （x3）x24x+3（x2）21， 该抛物线的对称轴是直线 x2， 故答案为：2 【点评】本题考查二次函数的性质，解答本题的关键是明确题意，利用二次函数的性质解答 16 （4 分）如图，已知在ABC 中，ABAC以 AB 为直径作半圆 O，交 BC 于点 D若BA
24、C40， 则的度数是 140 度 【分析】首先连接 AD，由等腰ABC 中，ABAC，以 AB 为直径的半圆交 BC 于点 D，可得BAD CAD20，即可得ABD70，继而求得AOD 的度数，则可求得的度数 【解答】解：连接 AD、OD， AB 为直径， ADB90， 即 ADBC， ABAC， BADCADBAC20，BDDC， ABD70， AOD140 的度数为 140； 故答案为 140 【点评】此题考查了圆周角定理以及等腰三角形的性质此题难度适中，注意掌握辅助线的作法，注意 掌握数形结合思想的应用 17 （4 分）如图，在ABC 中，D、E、F 分别在 AB、AC、BC 上，DEB
25、C，EFAB，AD：BD5：3， CF6，则 DE 的长为 10 【分析】根据平行线分线段成比例定理得到，证明AEDECF，根据相似三角形的性 质列出比例式，代入计算得到答案 【解答】解：DEBC， ，AEDC， EFAB， CEFA，又AEDC， AEDECF， ，即， 解得，DE10， 故答案为：10 【点评】本题考查的是相似三角形的判定和性质、平行线分线段成比例定理，掌握相似三角形的判定定 理和性质定理是解题的关键 18 （4 分）如图，已知O 的半径为 2，弦 AB2，点 P 为优弧上动点，点 I 为PAB 的内心，当 点 P 从点 A 向点 B 运动时，点 I 移动的路径长为 【分析
26、】连接 OB，OA，过 O 作 ODAB，得到 ADBDAB，求得PAOB60，连 接 IA，IB，根据角平分线的定义得到IABPAB，IBAPBA，根据三角形的内角和得到 AIB180 （PAB+PBA） 120， 设 A， B， I 三点所在的圆的圆心为 O， 连接 OA， OB， 得到AOB120，根据等腰三角形的性质得到OABOBA30，连接 OD，解直角三 角形得到 AO2，根据弧长公式即可得到结论 【解答】解：连接 OB，OA，过 O 作 ODAB， ADBDAB， OAOB2， OD1， AODBOD60， AOB120， PAOB60， 连接 IA，IB， 点 I 为PAB 的
27、内心， IABPAB，IBAPBA， PAB+PBA120， AIB180（PAB+PBA）120， 点 P 为弧 AB 上动点， P 始终等于 60， 点 I 在以 AB 为弦，并且所对的圆周角为 120的一段劣弧上运动， 设 A，B，I 三点所在的圆的圆心为 O， 连接 OA，OB， 则AOB120， OAOB， OABOBA30， 连接 OD， ADBD， ODAB， AO2， 点 I 移动的路径长 故答案为： 【点评】本题考查的是三角形的内切圆与内心，根据题意作出辅助线，构造出全等三角形，得出点 I 在 以 AB 为弦，并且所对的圆周角为 120的一段劣弧上是解答此题的关键 三、解答题
28、（本大题有三、解答题（本大题有 8 小题，第小题，第 19 题题 6 分，第分，第 20，21，22 题各题各 8 分，第分，第 23 题题 10 分，第分，第 24 题题 12 分，分， 第第 25 题题 12 分，第分，第 26 题题 14 分，共分，共 78 分）分） 19 （6 分）计算：|+202002sin30+ 【分析】首先计算乘方、开方，然后计算乘法，最后从左向右依次计算，求出算式的值是多少即可 【解答】解：|+202002sin30+ +12+2 3 【点评】此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和 有理数运算一样，要从高级到低级，即
29、先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号 里面的，同级运算要按照从左到右的顺序进行另外，有理数的运算律在实数范围内仍然适用 20 （8 分）我区某中学举行了“垃圾分类，绿色环保”知识竞赛活动，根据学生的成绩划分为 A，B，C， D 四个等级，并绘制了不完整的两种统计图： 根据图中提供的信息，回答下列问题： （1）参加知识竞赛的学生共有 40 人，并把条形统计图补充完整； （2）扇形统计图中，m 10 ，n 40 ，C 等级对应的圆心角为 144 度； （3）小明是四名获 A 等级的学生中的一位，学校将从获 A 等级的学生中任选取 2 人，参加区举办的知 识竞赛，请用列表法或画树
30、状图，求小明被选中参加区知识竞赛的概率 【分析】 （1）从两个统计图可得， “D 级”的有 12 人，占调查人数的 30%，可求出调查人数；进而求出 “B 级”的人数，即可补全条形统计图； （2）计算出“A 级”所占的百分比， “C 级”所占的百分比，进而求出“C 级”所对应的圆心角的度数； （3）用列表法列举出所有等可能出现的情况，从中找出符合条件的情况数，进而求出概率 【解答】解： （1）1230%40 人，4020%8 人， 故答案为：40，补全条形统计图如图所示： （2）44010%，164040%， 36040%144 故答案为：10，40，144； （3）设除小明以外的三个人记作
31、A、B、C，从中任意选取 2 人，所有可能出现的情况如下： 共有 12 中可能出现的情况，其中小明被选中的有 6 种， 所以小明被选中参加区知识竞赛的概率为 【点评】考查扇形统计图、条形统计图的意义和制作方法，从统计图中获取数量及数量之间的关系是解 决问题的关键，样本估计总体是统计中常用的方法 21 （8 分）已知二次函数 yx22x3 （1）求函数图象的顶点坐标，与坐标轴的交点坐标，并画出函数的大致图象； （2）根据图象直接回答：当 y0 时，求 x 的取值范围；当 y3 时，求 x 的取值范围 【分析】 （1）利用配方法得到 y（x1）24，从而得到抛物线的顶点坐标，再计算自变量为 0 对
32、应的 函数值得到抛物线与 y 轴的交点坐标，通过解方程 x22x30 得抛物线与 x 轴的交点坐标，然后利用 描点法画函数图象； （2）结合函数图象，当 y0 时，写出函数图象在 x 轴下方所对应的自变量的范围；当 y3 时，写出 函数值大于3 对应的自变量的范围 【解答】解： （1）yx22x3（x1）24， 抛物线的顶点坐标为（1，4） ， 当 x0 时，yx22x33，则抛物线与 y 轴的交点坐标为（0，3） ， 当 y0 时，x22x30，解得 x11，x23，则抛物线与 x 轴的交点坐标为（1，0） ， （3，0） ， 如图， （2）当1x3 时，y0； 当 x0 或 x2 时，y3
33、 【点评】本题考查了抛物线与 x 轴的交点：把求二次函数 yax2+bx+c（a，b，c 是常数，a0）与 x 轴 的交点坐标问题转化为解关于 x 的一元二次方程也考查了二次函数的性质 22 （8 分）如图，某航天飞机在地球表面点 P 的正上方 A 处，从 A 处观测到地球上的最远点 Q，即 AQ 是 O 的切线，若QAP，地球半径为 R， 求： （1）航天飞机距地球表面的最近距离 AP 的长； （2）P、Q 两点间的地面距离，即的长 （注：本题最后结果均用含 ，R 的代数式表示） 【分析】 （1）连接 OQ，根据题意可得：AQ 是O 的切线，然后由切线的性质，可得 OQAQ，又由 QAP，地
34、球半径为 R，即可求得 OA 的长，继而求得航天飞船距离地球表面的最近距离 AP 的值； （2）在直角OAQ 中，可求出O 的度数，再利用弧长公式计算即可 【解答】解： （1）由题意，从 A 处观测到地球上的最远点 Q， AQ 是O 的切线，切点为 Q， 连接 OQ，则 OQ 垂直于 AQ，如图 则在直角OAQ 中有sin， 即 APR； （2）在直角OAQ 中 则O90， 由弧长公式得的长 【点评】此题考查了切线的性质与解直角三角形的应用此题难度不大，注意掌握辅助线的作法，注意 数形结合思想的应用 23 （10 分）如图，直线 MN 交O 于 A，B 两点，AC 是O 直径，CAM 的平分线
35、交O 于点 D，过点 D 作 DEMN 于点 E （1）求证：DE 是O 的切线； （2）若 DE6cm，AE3cm，求O 的半径 【分析】 （1）连接 OD，由等腰三角形的性质得出32，证出13，得出 MNOD，证出 DE OD，即可得出 DE 是O 的切线； （2）连接 CD，由圆周角定理得出ADC90，由勾股定理求出 AD，根据相似三角形的性质即可得 到结论 【解答】 （1）证明：连接 OD，如图所示： OAOD， 32， AD 平分CAM， 21， 13， MNOD， DEMN， DEOD， DE 是O 的切线； （2）解：连接 CD，如图所示： AC 是O 的直径， ADC90， A
36、D3（cm） ， DEMN， AED90， ADCAED， 又21， ADCAED， ， 即， AC15（cm） ， OAACcm， 即O 的半径为cm 【点评】 本题考查了切线的判定、 等腰三角形的性质、 平行线的判定与性质、 相似三角形的判定与性质、 勾股定理等知识；本题综合性强，有一定难度 24 （12 分） （1）如图 1，在平行四边形 ABCD 中，点 E1，E2是 AB 三等分点，点 F1，F2是 CD 三等分点， E1F1，E2F2分别交 AC 于点 G1，G2，求证：AG1G1G2G2C （2）如图 2，由 64 个边长为 1 的小正方形组成的一个网格图，线段 MN 的两个端点
37、在格点上，请用一 把无刻度的尺子，画出线段 MN 三等分点 P，Q （保留作图痕迹） 【分析】 （1）利用平行线分线段成比例定理证明即可 （2）利用（1）中结论，构造平行四边形解决问题即可 【解答】 （1）证明：如图 1 中， 四边形 ABCD 是平行四边形， ABCD，ABCD，ADBC， DF1CD，AE1AB， DF1AE1， 四边形 ADF1E1是平行四边形， ADE1F1， E1G1BC， ， 同法可证：， AG1CG2AC， AG1G1G2G2C （2）如图，点 P，Q 即为所求 【点评】本题考查则有应用与设计，平行四边形的性质，平行线分线段成比例定理等知识，解题的关 键是理解题意
38、，灵活运用所学知识解决问题 25（12 分） 每年十月的第二个周四是世界爱眼日， 为预防近视， 超市决定对某型号护眼台灯进行降价销售 降 价前，进价为 30 元的护眼台灯以 80 元售出，平均每月能售出 200 盏，调查表明：这种护眼台灯每盏售 价每降低 1 元，其月平均销售量将增加 10 盏 （1）写出月销售利润 y（单位：元）与销售价 x（单位：元/盏）之间的函数表达式； （2）当销售价定为多少元时，所得月利润最大？最大月利润为多少元？ 【分析】 （1）根据“总利润单件利润销售量”可得； （2）利用配方法求出二次函数最值即可得出答案 【解答】解： （1）设售价为 x 元/盏，月销售利润 y
39、 元，根据题意得： y（x30）200+10（80 x）10 x2+1300 x30000； （2）y10 x2+1300 x3000010（x65）2+12250， 当销售价定为 65 元时，所得月利润最大，最大月利润为 12250 元 【点评】此题主要考查了二次函数的应用以及二次函数最值求法，解题关键是要读懂题目的意思，根据 题目给出的条件，找出合适的等量关系 26 （14 分）问题提出： 如图 1，在等边ABC 中，AB9，C 半径为 3，P 为圆上一动点，连结 AP，BP，求 AP+BP 的最小 值 （1）尝试解决： 为了解决这个问题，下面给出一种解题思路，通过构造一对相似三角形，将B
40、P 转化为某一条线段长， 具体方法如下： （请把下面的过程填写完整） 如图 2，连结 CP，在 CB 上取点 D，使 CD1，则有 又PCD BCP PCD BCP PDBP AP+BPAP+PD 当 A，P，D 三点共线时，AP+PD 取到最小值 请你完成余下的思考，并直接写出答案：AP+BP 的最小值为 （2）自主探索： 如图 3，矩形 ABCD 中，BC6，AB8，P 为矩形内部一点，且 PB4，则AP+PC 的最小值为 2 （请在图 3 中添加相应的辅助线） （3）拓展延伸： 如图 4，在扇形 COD 中，O 为圆心，COD120，OC4OA2，OB3，点 P 是上一点，求 2PA+P
41、B 的最小值，画出示意图并写出求解过程 【分析】 （1）连结 AD，过点 A 作 AFCB 于点 F，AP+BPAP+PD，要使 AP+BP 最小，AP+AD 最 小，当点 A，P，D 在同一条直线时，AP+AD 最小，即可求解； （2）在 AB 上截取 BF2，连接 PF，PC，AB8，PB4，BF2，证明ABPPBF，当点 F，点 P， 点 C 三点共线时，AP+PC 的值最小，即可求解； （3）延长 OC，使 CF4，连接 BF，OP，PF，过点 F 作 FBOD 于点 M，确定，且AOP AOP，AOPPOF，当点 F，点 P，点 B 三点共线时，2AP+PB 的值最小，即可求解 【解
42、答】解： （1）如图 1， 连结 AD，过点 A 作 AFCB 于点 F， AP+BPAP+PD，要使 AP+BP 最小， AP+AD 最小，当点 A，P，D 在同一条直线时，AP+AD 最小， 即：AP+BP 最小值为 AD， AC9，AFBC，ACB60 CF，AF， DFCFCD32， AD AP+BP 的最小值为； 故答案为：； （2）如图 2， 在 AB 上截取 BF2，连接 PF，PC， AB8，PB4，BF2， ，且ABPABP， ABPPBF， ，PFAP AP+PCPF+PC， 当点 F，点 P，点 C 三点共线时，AP+PC 的值最小， CF2， ，AP+PC 的值最小值为
43、 2， 故答案为：2； （3）如图 3， 延长 OC，使 CF4，连接 BF，OP，PF，过点 F 作 FBOD 于点 M， OC4，FC4， FO8，且 OP4，OA2， ，且AOPAOP AOPPOF ， PF2AP 2PA+PBPF+PB， 当点 F，点 P，点 B 三点共线时，2AP+PB 的值最小， COD120， FOM60，且 FO8，FMOM OM4，FM4 MBOM+OB4+37 FB 2PA+PB 的最小值为 【点评】此题是圆的综合题，主要考查了圆的有关知识，勾股定理，相似三角形的判定和性质，极值的 确定，还考查了学生的阅读理解能力，解本题的关键是根据材料中的思路构造出相似三角形，也是解本 题的难点
