1、 2020 年人教版八年级上册第年人教版八年级上册第 14 章整式的乘法与因式分解单元测试卷章整式的乘法与因式分解单元测试卷 一选择题（共一选择题（共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 1下列各式中计算结果为 x6的是（ ） Ax2+x4 Bx8x2 Cx2x4 Dx12x2 2下列运算中，正确的是（ ） A3a+2b5ab B （3a）29a2 Ca6a3a2 D （a+1）2a2+1 3下列因式分解正确的是（ ） Ax2x+（x）2 Ba4b6a3b+9a2ba2b（a26a+9） Cx22x+4（x2）2 D4x2y2（4x+y） （4xy） 4若多项
2、式 x2+2x+n 是完全平方公式，则常数 n 是（ ） A1 B C D1 5把多项式 x2+mx5 因式分解成（x+5） （x1） ，则 m 的值为（ ） Am6 Bm6 Cm4 Dm4 6若 M（x3） （x4） ，N（x1） （x6） ，则 M 与 N 的大小关系为（ ） AMN BMN CMN D由 x 的取值而定 7若 a2+2ab+b2c210，a+b+c5，则 a+bc 的值是（ ） A2 B5 C20 D9 8如图，现有正方形卡片 A 类，B 类和长方形卡片 C 类若干张，如果要拼一个长为（a+3b） ，宽为（a+2b） 的大长方形，则需要 C 类卡片（ ） A3 张 B4
3、张 C5 张 D6 张 9如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“和平数” 如 42202，12 4222，因此 4，12 这两个数都是“和平数” 介于 1 到 301 之间的所有“和平数“之和为（ ） A5776 B4096 C2020 D108 10如图，大正方形的边长为 m，小正方形的边长为 n，x，y 表示四个相同长方形的两边长（xy） 则x yn；xy；x2y2mn；x2+y2中，正确是（ ） A B C D 二填空题（共二填空题（共 6 小题，满分小题，满分 24 分，每小题分，每小题 4 分）分） 11已知（x2） （x2+mx+n）的乘积项中不含 x2和
4、 x 项，则 m+n 12计算： （0.25）202142020 13 （8a3b4a2b2）2ab 14若 a2+b216，ab6，则 ab 15分解因式：3ma23mb 16计算： （3）0（2）2 三解答题（共三解答题（共 7 小题，满分小题，满分 66 分）分） 17 （6 分）计算： （1）a4+（a2）4（a3）2a2 （2）2019220202018（用简便方法计算） 18 （16 分）计算： （1） （2x）2 （2x2x） （2）a2（2ab）+3a（a2b1） （3） （2ab2）2 （3a2b2ab4b） （4）2ab（a2b+abab2）ab2（a23ab+2a） 19
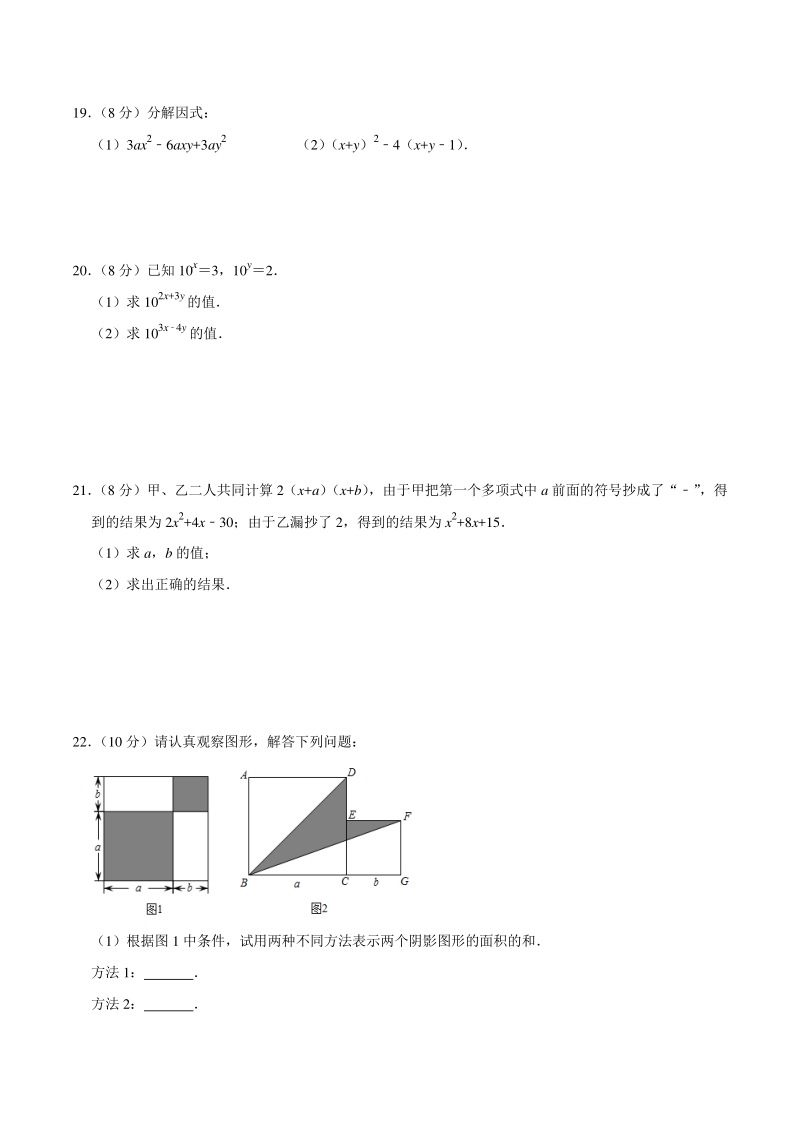
5、 （8 分）分解因式： （1）3ax26axy+3ay2 （2） （x+y）24（x+y1） 20 （8 分）已知 10 x3，10y2 （1）求 102x+3y的值 （2）求 103x 4y 的值 21 （8 分）甲、乙二人共同计算 2（x+a） （x+b） ，由于甲把第一个多项式中 a 前面的符号抄成了“” ，得 到的结果为 2x2+4x30；由于乙漏抄了 2，得到的结果为 x2+8x+15 （1）求 a，b 的值； （2）求出正确的结果 22 （10 分）请认真观察图形，解答下列问题： （1）根据图 1 中条件，试用两种不同方法表示两个阴影图形的面积的和 方法 1： 方法 2： （2）从
6、中你能发现什么结论？请用等式表示出来： （3）利用（2）中结论解决下面的问题： 如图 2，两个正方形边长分别为 a、b，如果 a+bab9，求阴影部分的面积 23 （10 分）从边长为 a 的正方形中剪掉一个边长为 b 的正方形（如图 1） ，然后将剩余部分拼成一个长方 形（如图 2） （1）上述操作能验证的等式是 （请选择正确的选项） Aa2b2（a+b） （ab） Ba22ab+b2（ab）2 Ca2+aba（a+b） （2）若 x2y216，x+y8，求 xy 的值； （3）计算： （1） （1） （1）（1） （1） 参考答案参考答案 一选择题（共一选择题（共 10 小题，满分小题，满
7、分 30 分，每小题分，每小题 3 分）分） 1解：x2与 x4不是同类项，不能合并计算，它是一个多项式，因此 A 选项不符合题意； 同理选项 B 不符合题意； x2x4x2+4x6，因此选项 C 符合题意； x12x2x12 2x10，因此选项 D 不符合题意； 故选：C 2解：A、3a 与 2b 不是同类项，不能合并，此选项错误； B、 （3a）29a2，此选项正确； C、a6a3a3，此选项错误； D、 （a+1）2a2+2a+1，此选项错误； 故选：B 3解：A、x2x+（x）2，正确； B、a4b6a3b+9a2ba2b（a26a+9）a2b（a3）2，故此选项错误； C、x22x+
8、4，无法运用公式法分解因式，故此选项错误； D、4x2y2（2x+y） （2xy） ，故此选项错误； 故选：A 4解：多项式 x2+2x+n 是一个完全平方式， x2+2x+n（x+1）2， n1 故选：D 5解：由题意，得 m514 故选：D 6解：M（x3） （x4）x27x+12； N（x1） （x6）x27x+6； MN60； MN； 故选：A 7解：a2+2ab+b2c210， （a+b）2c210， （a+b+c） （a+bc）10， a+b+c5， 5（a+bc）10， 解得 a+bc2 故选：A 8解：（a+3b） （a+2b）a2+2ab+3ab+6b2a2+5ab+6b2，
9、 需要 A 类卡片 1 张、B 类卡片 6 张、C 类卡片 5 张， 故选：C 9解：300762742， 介于 1 到 301 之间的所有“和平数“之和为：762742+742722+722702+22027625776， 故选：A 10解：xy 等于小正方形的边长，即 xyn，正确； xy 为小长方形的面积， xy， 故本项正确； x2y2（x+y） （xy）mn，故本项正确； x2+y2（x+y）22xym22， 故本项错误 所以正确的有 故选：A 二填空题（共二填空题（共 6 小题，满分小题，满分 24 分，每小题分，每小题 4 分）分） 11解： （x2） （x2+mx+n）x3+m
10、x2+nx2x22mx2n x3+（m2）x2+（n2m）x2n （x2） （x2+mx+n）的乘积项中不含 x2和 x 项， m20，n2m0， 解得：m2，n2， m+n4 故答案为：4 12解： （0.25）202142020 （0.25）202042020（0.25） （0.254）2020（0.25） 1（0.25） 0.25 故答案为：0.25 13解： （8a3b4a2b2）2ab 8a3b2ab4a2b22ab 4a22ab 故答案为：4a22ab 14解：ab6， （ab）236， a2+b22ab36， a2+b216， 162ab36， ab10， 故答案为：10 15解
11、：原式3m（a2b） 16解：原式14， 故答案为： 三解答题（共三解答题（共 7 小题，满分小题，满分 66 分）分） 17解： （1）原式a4+a8a6a2 a4+a8a4 a8； （2）原式20192（2019+1）（20191） 2019220192+1 1 18解： （1） （2x）2 （2x2x） 4x2 （2x2x） 4x22x2x4x24x2 8x4x3x2； （2）a2（2ab）+3a（a2b1） 2a3b+3aa2b13a 2a3b+3a3b3a 5a3b3a； （3） （2ab2）2 （3a2b2ab4b） 4a2b4 （3a2b2ab4b） 4a2b43a2b4a2b4
12、2ab4a2b44b 12a4b58a3b516a2b5； （4）2ab（a2b+abab2）ab2（a23ab+2a） 2aba2b+ab2abab22abab2a23ab （ab2）+2a （ab2） 2a3b2+2a2b22a2b3a3b2+3a2b32a2b2 a3b2+a2b3 19解： （1）原式3a（x22xy+y2） 3a（xy）2； （2）原式（x+y）24（x+y）+4 （x+y2）2 20解： （1）102x+3y102x103y（10 x）2 （10y）39872； （2）103x 4y103x104y（10 x）3（10y）42716 21解： （1）甲把第一个多项式
13、中 a 前面的符号抄成了“” ，得到的结果为 2x2+4x30， 2（xa） （x+b） 2x2+2bx2ax2ab 2x2+（2b2a）x2ab 2x2+4x30， 2b2a4， 乙漏抄了 2，得到的结果为 x2+8x+15， （x+a） （x+b） x2+bx+ax+ab x2+（a+b）x+ab x2+8x+15， a+b8， 解方程组得：， 即 a3，b5； （2）2（x+3） （x+5） 2x2+10 x+6x+30 2x2+16x+30 22解： （1）图 1，两个阴影正方形的面积和：a2+b2， 大正方形的面积减去两个长方形的面积： （a+b）22ab， 故答案为：a2+b2，
14、（a+b）22ab； （2）两个数的平方和等于这两个数和的平方减去这两个数积的 2 倍，即：a2+b2（a+b）22ab； 故答案为：a2+b2（a+b）22ab； （3）如图 2，阴影部分的面积为： a2+b2（a+b）b a2ab+b2 （a+b）2ab 27 23解： （1）图 1 的剩余面积为 a2b2，图 2 拼接得到的图形面积为（a+b） （ab） 因此有，a2b2（a+b） （ab） ， 故答案为：A （2）x2y2（x+y） （xy）16， 又x+y8， xy1682； （3）原式（1） （1+） （1） （1+） （1） （1+）（1） （1+） （1） （1+） ， ， ，
