1、2021 年广东省中山市中考数学仿真模拟试卷年广东省中山市中考数学仿真模拟试卷 一选择题（共一选择题（共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 1在3，1，1，3 四个数中，比 2 大的数是（ ） A3 B1 C1 D3 2下列计结果为 a10的是（ ） Aa6+a4 Ba11a C（a5）2 Da20a2 3截止到 2019 年 9 月 3 日，电影哪吒之魔童降世的累计票房达到了 47.24 亿，47.24 亿用科学记数法 表示为（ ） A47.24109 B4.724109 C4.724105 D472.4105 4下列图案中是中心对称图形但不是轴对称图形的
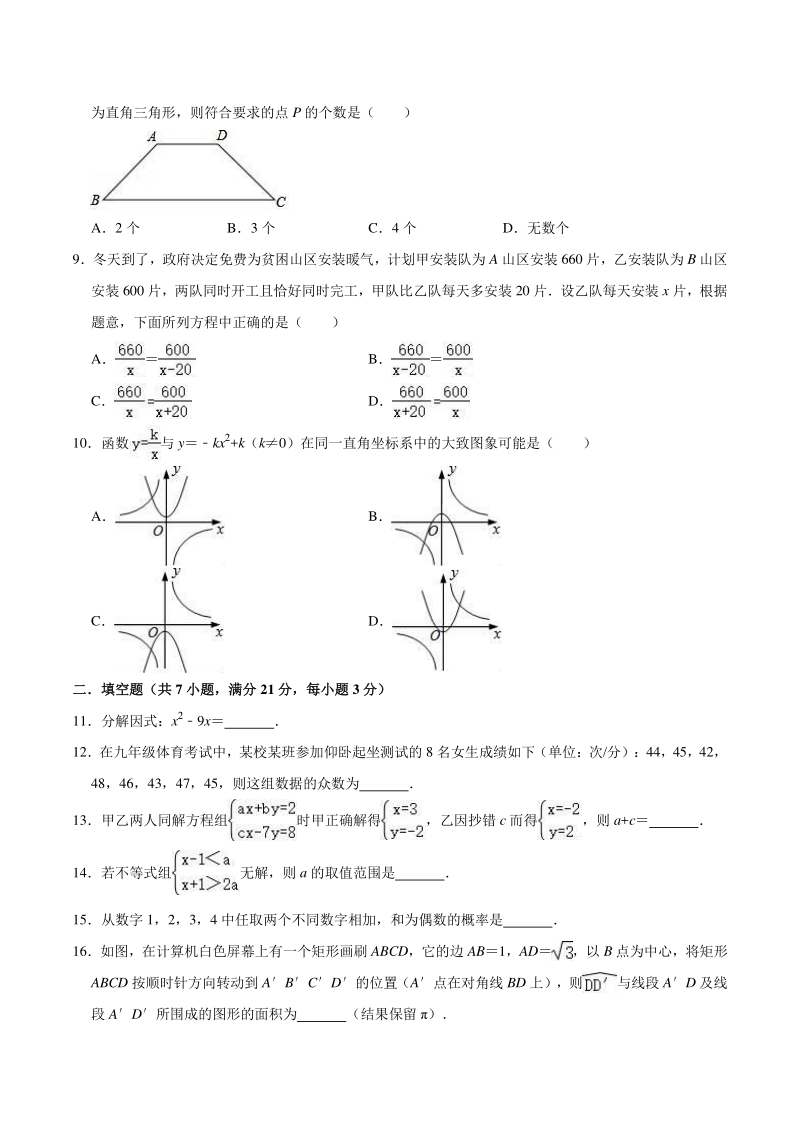
2、是（ ） A B C D 5式子有意义的 x 的取值范围是（ ） Ax且 x1 Bx1 C Dx且 x1 6甲、乙、丙、丁四个同学在三次阶段考试中数学成绩的方差分别为 s甲 20.12，s 乙 20.19，S 丙 20.21， s 丁 20.10，则成绩最稳定的是（ ） A甲 B乙 C丙 D丁 7如图，ABCD 为一长条形纸带，ABCD，将 ABCD 沿 EF 折叠，A、D 两点分别与 A、D对应，若 122，则AEF 的度数为（ ） A60 B65 C72 D75 8如图，在四边形 ABCD 中，ADBC，AD4，BC6，ABCD2，若点 P 在线段 BC 上，且ADP 为直角三角形，则符合
3、要求的点 P 的个数是（ ） A2 个 B3 个 C4 个 D无数个 9冬天到了，政府决定免费为贫困山区安装暖气，计划甲安装队为 A 山区安装 660 片，乙安装队为 B 山区 安装 600 片，两队同时开工且恰好同时完工，甲队比乙队每天多安装 20 片设乙队每天安装 x 片，根据 题意，下面所列方程中正确的是（ ） A B C D 10函数与 ykx2+k（k0）在同一直角坐标系中的大致图象可能是（ ） A B C D 二填空题（共二填空题（共 7 小题，满分小题，满分 21 分，每小题分，每小题 3 分）分） 11分解因式：x29x 12在九年级体育考试中，某校某班参加仰卧起坐测试的 8
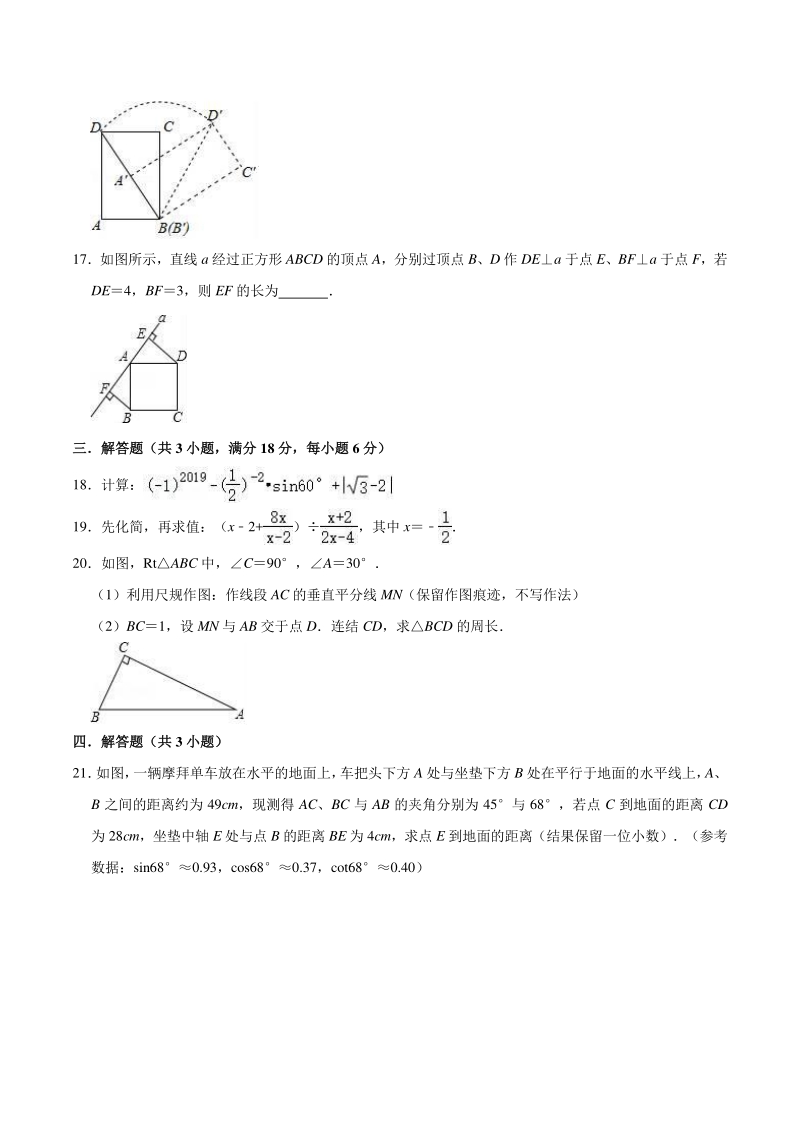
4、名女生成绩如下（单位：次/分）：44，45，42， 48，46，43，47，45，则这组数据的众数为 13甲乙两人同解方程组时甲正确解得，乙因抄错 c 而得，则 a+c 14若不等式组无解，则 a 的取值范围是 15从数字 1，2，3，4 中任取两个不同数字相加，和为偶数的概率是 16如图，在计算机白色屏幕上有一个矩形画刷 ABCD，它的边 AB1，AD，以 B 点为中心，将矩形 ABCD 按顺时针方向转动到 ABCD的位置（A点在对角线 BD 上），则与线段 AD 及线 段 AD所围成的图形的面积为 （结果保留 ） 17如图所示，直线 a 经过正方形 ABCD 的顶点 A，分别过顶点 B、D
5、 作 DEa 于点 E、BFa 于点 F，若 DE4，BF3，则 EF 的长为 三解答题（共三解答题（共 3 小题，满分小题，满分 18 分，每小题分，每小题 6 分）分） 18计算： 19先化简，再求值：（x2+），其中 x 20如图，RtABC 中，C90，A30 （1）利用尺规作图：作线段 AC 的垂直平分线 MN（保留作图痕迹，不写作法） （2）BC1，设 MN 与 AB 交于点 D连结 CD，求BCD 的周长 四解答题（共四解答题（共 3 小题）小题） 21 如图， 一辆摩拜单车放在水平的地面上， 车把头下方 A 处与坐垫下方 B 处在平行于地面的水平线上， A、 B 之间的距离约为
6、 49cm，现测得 AC、BC 与 AB 的夹角分别为 45与 68，若点 C 到地面的距离 CD 为 28cm，坐垫中轴 E 处与点 B 的距离 BE 为 4cm，求点 E 到地面的距离（结果保留一位小数）（参考 数据：sin680.93，cos680.37，cot680.40） 22如图，已知反比例函数 y1与一次函数 y2k2x+b 的图象交于点 A（1，8），B（4，m）两点 （1）求 k1，k2，b 的值； （2）求AOB 的面积； （3）请直接写出不等式x+b 的解 23美化城市，改善人们的居住环境已成为城市建设的一项重要内容我市近几年来，通过拆迁旧房，植 草，栽树，修公园等措施，
7、使城区绿地面积不断增加（如图所示） （1）根据图中所提供的信息回答下列问题：2003 年底的绿地面积为 公顷，比 2002 年底增加了 公顷；在 2001 年，2002 年，2003 年这三个中，绿地面积最多的是 年； （2）为满足城市发展的需要，计划到 2005 年底使城区绿地面积达到 72.6 公顷，试求 2004 年，2005 年 的年平均增长率 五解答题（共五解答题（共 2 小题）小题） 24如图 1，在平面直角坐标系内，A，B 为 x 轴上两点，以 AB 为直径的M 交 y 轴于 C，D 两点，C 为 的中点，弦 AE 交 y 轴于点 F，且点 A 的坐标为（2，0），CD8 （1）
8、求M 的半径； （2）动点 P 在M 的圆周上运动 如图 1，当 EP 平分AEB 时，求 PNEP 的值； 如图 2，过点 D 作M 的切线交 x 轴于点 Q，当点 P 与点 A，B 不重合时，是否为定值？若是，请 求出其值；若不是，请说明理由 25如图 1，在矩形纸片 ABCD 中，AB12cm，AD20cm，折叠纸片使 B 点落在边 AD 上的 E 处，折痕为 PQ，过点 E 作 EFAB 交 PQ 于 F，连接 BF （1）求证：四边形 BFEP 为菱形； （2）当点 E 在 AD 边上移动时，折痕的端点 P、Q 也随之移动； 当点 Q 与点 C 重合时（如图 2），求菱形 BFEP
9、的边长； 若限定 P、Q 分别在边 BA、BC 上移动，求出点 E 在边 AD 上移动的最大距离 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 10 小题，满分小题，满分 30 分，每小题分，每小题 3 分）分） 1【分析】根据有理数比较大小的方法解答即可 【解答】解：比 2 大的数是 3 故选：D 【点评】此题主要考查了有理数比较大小，正确把握有理数比较大小的方法是解题关键 2【分析】分别根据合并同类项法则，幂的乘方运算法则以及同底数幂的除法法则逐一判断即可 【解答】解：Aa6与 a4不是同类项，所以不能合并，故本选项不合题意； Ba11与a 不是同类项，所以不能合并，故本
10、选项不合题意； C（a5）2a10，符合题意； Da20a2a18，故本选项不合题意 故选：C 【点评】本题主要考查了合并同类项，同底数幂的除法以及幂的乘方与积的乘方，熟记幂的运算法则是 解答本题的关键 3【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，要看把 原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同当原数绝对值1 时，n 是 正数；当原数的绝对值1 时，n 是负数 【解答】解：47.24 亿4724 000 0004.724109 故选：B 【点评】此题考查科学记数法的表示方法科学记数法的表示形式为 a10n的形
11、式，其中 1|a|10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值 4【分析】根据轴对称图形与中心对称图形的概念求解 如果一个图形沿着一条直线对折后两部分完全重合， 这样的图形叫做轴对称图形， 这条直线叫做对称轴 如果一个图形绕某一点旋转 180后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做 对称中心 【解答】解：A、是中心对称图形，也是轴对称图形，不符合题意； B、不是中心对称图形，是轴对称图形，不符合题意； C、是中心对称图形，不是轴对称图形，符合题意； D、不是轴对称图形，也不是中心对称图形，不符合题意 故选：C 【点评】此题主要考查了中心对称图形与轴对称图形
12、的概念轴对称图形的关键是寻找对称轴，图形两 部分沿对称轴折叠后可重合，中心对称图形是要寻找对称中心，图形旋转 180 度后与原图形重合 5【分析】根据被开方数是非负数且分母不等于零，可得答案 【解答】解：由题意，得 2x+10 且 x10， 解得 x且 x1， 故选：A 【点评】本题考查了二次根式有意义的条件，利用被开方数是非负数且分母不等于零得出不等式是解题 关键 6【分析】由题意易得 s丁 2s 甲 2s 乙 2S 丙 2，根据方差的意义（方差反映一组数据的波动大小，方差越 小，波动越小，越稳定）即可得到答案 【解答】解：s 甲 20.12，s 乙 20.19，S 丙 20.21，s 丁
13、20.10， s 丁 2s 甲 2s 乙 2S 丙 2， 成绩最稳定的是丁 故选：D 【点评】本题考查了方差的意义：方差反映一组数据的波动大小，方差越小，波动越小，越稳定 7【分析】由题意122，设2x，易证AEF1FEA2x，构建方程即可解决问题 【解答】解：由翻折的性质可知：AEFFEA， ABCD， AEF1， 122，设2x，则AEF1FEA2x， 5x180， x36， AEF2x72， 故选：C 【点评】本题考查平行线的性质，翻折变换等知识，解题的关键是学会利用参数解决问题，属于中考常 考题型 8【分析】分别以PAD90、ADP90和APD90三种情况作图可得 【解答】解：如图所示
14、， 符合要求的点 P 的个数是 4 个， 故选：C 【点评】本题主要考查圆周角定理，解题的关键是掌握分类讨论思想的运用与圆周角定理 9【分析】直接利用两队同时开工且恰好同时完工得出等式即可 【解答】解：设乙队每天安装 x 片，根据题意，列方程得： 故选：D 【点评】此题主要考查了由实际问题抽象出分式方程，正确表示出安装所用时间是解题关键 10 【分析】本题可先由反比例函数的图象得到字母系数的正负，再与二次函数的图象相比较看是否一致 【解答】解：由解析式 ykx2+k 可得：抛物线对称轴 x0； A、由双曲线的两支分别位于二、四象限，可得 k0，则k0，抛物线开口方向向上、抛物线与 y 轴 的交
15、点为 y 轴的负半轴上；本图象与 k 的取值相矛盾，故 A 错误； B、由双曲线的两支分别位于一、三象限，可得 k0，则k0，抛物线开口方向向下、抛物线与 y 轴 的交点在 y 轴的正半轴上，本图象符合题意，故 B 正确； C、由双曲线的两支分别位于一、三象限，可得 k0，则k0，抛物线开口方向向下、抛物线与 y 轴 的交点在 y 轴的正半轴上，本图象与 k 的取值相矛盾，故 C 错误； D、由双曲线的两支分别位于一、三象限，可得 k0，则k0，抛物线开口方向向下、抛物线与 y 轴 的交点在 y 轴的正半轴上，本图象与 k 的取值相矛盾，故 D 错误 故选：B 【点评】本题主要考查了二次函数及
16、反比例函数和图象，解决此类问题步骤一般为：（1）先根据图象的 特点判断 k 取值是否矛盾；（2）根据二次函数图象判断抛物线与 y 轴的交点是否符合要求 二填空题（共二填空题（共 7 小题，满分小题，满分 21 分，每小题分，每小题 3 分）分） 11【分析】首先确定多项式中的两项中的公因式为 x，然后提取公因式即可 【解答】解：原式xx9xx（x9）， 故答案为：x（x9） 【点评】本题考查了提公因式法因式分解的知识，解题的关键是首先确定多项式各项的公因式，然后提 取出来 12【分析】根据众数的定义即一组数据中出现次数最多的数，即可得出答案 【解答】解：45 出现了 2 次，出现的次数最多，
17、这组数据的众数为 45； 故答案为：45 【点评】此题考查了众数，掌握众数的定义是解题的关键；众数是一组数据中出现次数最多的数 13 【分析】 把代入得出 3c+148，求出 c， 把 和代入得出，求出 a， 再求出 a+c 即可 【解答】解： 把代入得：3c+148， 解得：c2， 把和代入得：， 解得：， 所以 a+c4+（2）2， 故答案为：2 【点评】本题考查了解二元一次方程组和二元一次方程组的解，能得出关于 c 的方程和得出关于 a、b 的 方程组是解此题的关键 14【分析】先求出每个不等式的解集，再根据已知不等式组无解得出关于 a 的不等式，求出不等式的解 集即可 【解答】解：，
18、由得，x1+a， 由得，x2a1， 由于不等式组无解，则 2a11+a 解得：a2 故答案为：a2 【点评】 本题考查了解一元一次不等式和解一元一次不等式组， 能得出关于 a 的不等式是解此题的关键 15【分析】根据题意画出树状图得出所有等情况数和和为偶数的情况数，然后根据概率公式即可得出答 案 【解答】解：根据题意画图如下： 共有 12 种等情况数，其中和为偶数的有 4 种， 则和为偶数的概率是； 故答案为： 【点评】此题考查的是用列表法或树状图法求概率列表法可以不重复不遗漏的列出所有可能的结果， 适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是 不
19、放回实验用到的知识点为：概率所求情况数与总情况数之比 16【分析】根据矩形的性质得到A90，根据勾股定理得到 BD2，根据旋转的性质 得到ABDABD60，ABAB2，ADAD，根据扇形和三角形的面积公 式即可得到结论 【解答】解：四边形 ABCD 是矩形， A90， AB1，AD， BD2， ADB30，ABD60， 将矩形 ABCD 按顺时针方向转动到 ABCD的位置， ABDABD60，ABAB2，ADAD， 与线段AD及线段AD所围成的图形的面积S扇形DBDSABD1 ， 故答案为： 【点评】本题考查了矩形的性质，勾股定理，特殊角的三角函数，旋转的性质，扇形面积的计算，正确 的理解题意
20、是解题的关键 17【分析】因为 ABCD 是正方形，所以 ABAD，ABCBAD90，则有ABFDAE，又因为 DEa、BFa，根据 AAS 易证AFBAED，所以 AFDE4，BFAE3，则 EF 的长可求 【解答】解：ABCD 是正方形 ABAD，ABCBAD90 ABC+ABFBAD+DAE ABFDAE 在AFB 和AED 中 ABFDAE，AFBAED，ABAD AFBAED AFDE4，BFAE3 EFAF+AE4+37 故答案为：7 【点评】此题把全等三角形的判定和正方形的性质结合求解考查学生综合运用数学知识的能力 三解答题（共三解答题（共 3 小题，满分小题，满分 18 分，每
21、小题分，每小题 6 分）分） 18【分析】首先计算乘方，然后计算乘法，最后从左向右依次计算，求出算式的值是多少即可 【解答】解： 14+2 【点评】此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和 有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号 里面的，同级运算要按照从左到右的顺序进行另外，有理数的运算律在实数范围内仍然适用 19【分析】先根据分式的混合运算顺序和运算法则化简原式，再将 x 的值代入计算可得 【解答】解：原式（+） 2（x+2） 2x+4， 当 x时， 原式2（）+4 1+4 3 【点评】本题主要考查
22、分式的化简求值，在化简的过程中要注意运算顺序和分式的化简化简的最后结 果分子、分母要进行约分，注意运算的结果要化成最简分式或整式 20【分析】（1）利用尺规作图：作线段 AC 的垂直平分线 MN 即可； （2）根据线段垂直平分线的性质即可求BCD 的周长 【解答】解：（1）如图，MN 即为所求； （2）连接 CD， ACB90，A30， BC1， BA2， MN 是 AC 垂直平分线， CDAD， ABBD+AD， CBCDCB+BA1+23， BCD 的周长是 3 【点评】本题考查了作图基本作图、线段的垂直平分线的性质，含 30 度角的直角三角形的性质，解决 本题的关键是掌握线段垂直平分线的
23、性质 四解答题（共四解答题（共 3 小题）小题） 21【分析】过点 C 作 CHAB 于点 H，过点 E 作 EF 垂直于 AB 延长线于点 F，设 CHx，则 AHCH x，BHCHcot680.4x，由 AB49 知 x+0.4x49，解之求得 CH 的长，再由 EFBEsin683.72 根据点 E 到地面的距离为 CH+CD+EF 可得答案 【解答】解：过点 C 作 CHAB 于点 H，过点 E 作 EF 垂直于 AB 延长线于点 F， 设 CHx，则 AHCHx，BHCHcot680.4x， 由 AB49 知 x+0.4x49， 解得：x35， BE4， EFBEsin683.72，
24、 则点 E 到地面的距离为 CH+CD+EF35+28+3.7266.7（cm）， 答：点 E 到地面的距离约为 66.7cm 【点评】本题主要考查解直角三角形的应用坡度坡角问题，解题的关键是理解题意构建直角三角形并 熟练掌握三角函数的定义 22【分析】（1）由点 A 的坐标利用反比例函数图象上点的坐标特征即可得出反比例函数解析式，再结合 点 B 的横坐标即可得出点 B 的坐标，根据点 A、B 的坐标利用待定系数法即可求出一次函数解析式； （2）根据一次函数图象上点的坐标特征求出一次函数图象与 y 轴的交点坐标，再利用分割图形法即可求 出AOB 的面积； （3）根据两函数图象的上下位置关系即可
25、得出不等式的解集 【解答】解： （1）反比例函数 y1与一次函数 y2k2x+b 的图象交于点 A（1，8）、B（4，m）， k18，B（4，2）， 解方程组，解得； （2）由（1）知一次函数 yk2x+b 的图象与 y 轴的交点坐标为（0，6）， SAOB 64+6115； （3）4x0 或 x1 【点评】本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及待定系数 法求一次函数解析式，解题的关键是：（1）根据点的坐标利用待定系数法求出函数解析式；（2）利用 分割图形法求出AOB 的面积；（3）根据两函数图象的上下位置关系找出不等式的解集 23【分析】（1）根据统计图能
26、看出 2001 年，2002 年，2003 年的绿地面积，进而求解即可； （2）设 2004 年，2005 年两年绿地面积的年平均增长率为 x，根据计划到 2005 年底使城区绿地面积达到 72.6 公顷，可列方程求解 【解答】解：（1）2003 年底的绿地面积为 60 公顷，2002 年底的绿地面积为为 56 公顷，2001 年底的绿 地面积为为 51 公顷， 60564，比 2002 年底增加了 4 公顷； 在 2001 年，2002 年，2003 年这三个中，绿地面积最多的是 2003 年 故答案，60，4，2003； （2）设 2004，2005 两年绿地面积的年平均增长率为 x， 6
27、0（1+x）272.6， x10%或 x210%（舍去） 答：2004，2005 两年绿地面积的年平均增长率 10% 【点评】本题考查一元二次方程的应用，折线统计图，从上面可看出每年对应的公顷数，以及 2003 年和 2005 年的公顷数，求出增长率 五解答题（共五解答题（共 2 小题）小题） 24【分析】（1）如图 1 中，连接 CM设 CMMAr，在 RtOCM 中，利用勾股定理构建方程即可解 决问题 （2）如图 2 中，连接 AP，BP证明APNEPA，推出，解直角三角形求出 PA 即可解 决问题 如图 3 中，连接 PM，DM证明DMOQMD，推出 DM2MOMQ，推出 MP2MOMQ
28、，推出 PMOQMP，可得，求出 QM 即可解决问题 【解答】解：（1）如图 1 中，连接 CM AMCD， OCOD4， 设 CMAMr， 在 RtCMO 中，CM2OC2+OM2， r242 +（r2）2， 解得 r5， M 的半径为 5 （2）如图 2 中，连接 AP，BP AB 是直径， APBAEB90， PE 平分AEP， AEPPEB45， ， PAPB， AB10，APB90， PAPBAB5， PANAEP45，APNAPE， APNEPA， ， PNPEPA250 如图 3 中，连接 PM，DM DQ 是M 的切线， DQDM， MDQMOD90， DMOQMD， DMOQ
29、MD， ， DM2MOMQ， MPMD， MP2MOMQ， ，PMOPMQ， PMOQMP， ， DM2MOMQ， 253MQ， MQ， 【点评】本题属于圆综合题，考查了垂径定理，圆周角定理，相似三角形的判定和性质，解直角三角形 等知识，解题的关键是学会添加常用辅助线，学会利用参数构建方程解决问题，学会正确寻找相似三角 形解决问题，属于中考压轴题 25【分析】（1）由折叠的性质得出 PBPE，BFEF，BPFEPF，由平行线的性质得出BPF EFP，证出EPFEFP，得出 EPEF，因此 BPBFEFEP，即可得出结论； （2）由矩形的性质得出 BCAD20cm，CDAB12cm，AD90，由
30、对称的性质得出 CE BC20cm，在 RtCDE 中，由勾股定理求出 DE16cm，得出 AEADDE4cm；在 RtAPE 中， 由勾股定理得出方程，解方程得出 EPcm 即可； 当点 Q 与点 C 重合时，点 E 离点 A 最近，由知，此时 AE4cm；当点 P 与点 A 重合时，点 E 离点 A 最远，此时四边形 ABQE 为正方形，AEAB3cm，即可得出答案 【解答】（1）证明：折叠纸片使 B 点落在边 AD 上的 E 处，折痕为 PQ， 点 B 与点 E 关于 PQ 对称， PBPE，BFEF，BPFEPF， 又EFAB， BPFEFP， EPFEFP， EPEF， BPBFEF
31、EP， 四边形 BFEP 为菱形； （2）四边形 ABCD 是矩形， BCAD20cm，CDAB12cm，AD90， 点 B 与点 E 关于 PQ 对称， CEBC20cm， 在 RtCDE 中，DE16cm， AEADDE20cm16cm4cm； 在 RtAPE 中，AE4，AP12PB12PE， EP242+（12EP）2， 解得：EPcm， 菱形 BFEP 的边长为cm； 当点 Q 与点 C 重合时，如图 2： 点 E 离点 A 最近，由知，此时 AE4cm； 当点 P 与点 A 重合时，如图 3 所示： 点 E 离点 A 最远，此时四边形 ABQE 为正方形，AEAB12cm， 点 E 在边 AD 上移动的最大距离为 8cm 【点评】本题是四边形综合题目，考查了矩形的性质、折叠的性质、菱形的判定、平行线的性质、等腰 三角形的判定、勾股定理、正方形的性质等知识；本题综合性强，有一定难度
