1、 第 1 页 / 共 26 页 第第 20 讲：导数的综合应用讲：导数的综合应用 一、课程标准 1、利用导数证明不等式有关的综合问题 2、利用导数研究零点有关的综合问题 3、通过使利润最大、用料最省、效率最高等优化问题，体会导数在解决实际问题中的作用. 二、基础知识回顾 1、逻辑推理是得到数学结论，构建数学体系的重要方式，是数学严谨性的基本保证利用两个经典不等式 解决问题，降低了思考问题的难度，优化了推理和运算过程 (1)对数形式：x1ln x(x0)，当且仅当 x1 时，等号成立 (2)指数形式：exx1(xR)，当且仅当 x0 时，等号成立进一步可得到一组不等式链：exx1x1 ln x(
2、x0，且 x1) 2、一般地，若 af(x)对 xD 恒成立，则只需 af(x)max；若 af(x)对 xD 恒成立，则只需 af(x0)成立， 则只需 af(x)min； 若存在 x0D， 使 af(x0)成立， 则只需 af(x0)max.由此构造不等式， 求解参数的取值范围 分类讨论法：常见有两种情况，一种先利用综合法，结合导函数零点之间大小关系的决定条件，确定 分类讨论的标准，分类后，判断不同区间函数的单调性，得到最值，构造不等式求解；另一种，直接通过 导函数的式子，看出导函数值正负的分类标准，通常导函数为二次函数或者一次函数 提示：求解参数范围时，一般会涉及分离参数法，理科试题中很
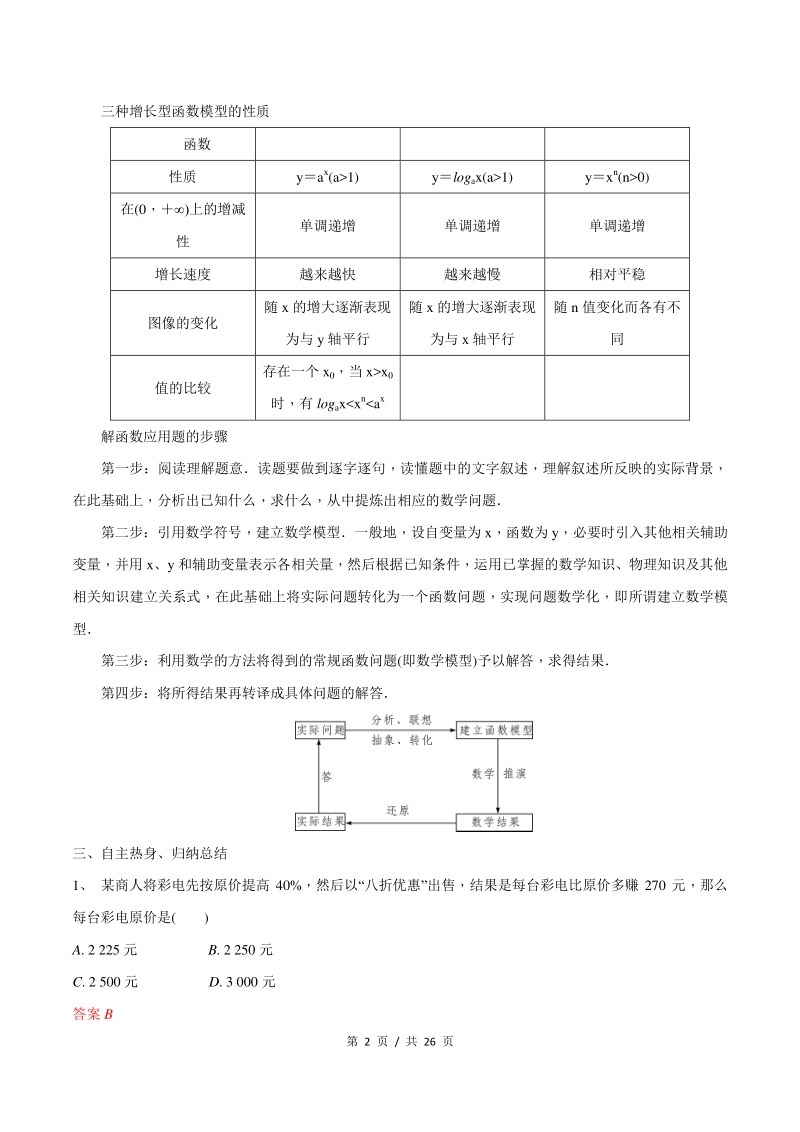
3、少碰到分离参数后构造的新函数能直 接求出最值点的情况，通常需要设出导函数的零点，难度较大 判断、证明或讨论函数零点个数的方法 利用零点存在性定理的条件为函数图象在区间a，b上是连 续不断的曲线， 且 f(a) f(b)0.直接法： 判断一个零点时， 若函数为单调函数， 则只需取值证明 f(a) f(b)0； 分类讨论法：判断几个零点时，需要先结合单调性，确定分类讨论的标准，再利用零点存在性定理，在 每个单调区间内取值证明 f(a) f(b)1) ylogax(a1) yxn(n0) 在(0，)上的增减 性 单调递增 单调递增 单调递增 增长速度 越来越快 越来越慢 相对平稳 图像的变化 随 x
4、 的增大逐渐表现 为与 y 轴平行 随 x 的增大逐渐表现 为与 x 轴平行 随 n 值变化而各有不 同 值的比较 存在一个 x0，当 xx0 时，有 logaxxnax 解函数应用题的步骤 第一步：阅读理解题意读题要做到逐字逐句，读懂题中的文字叙述，理解叙述所反映的实际背景， 在此基础上，分析出已知什么，求什么，从中提炼出相应的数学问题 第二步：引用数学符号，建立数学模型一般地，设自变量为 x，函数为 y，必要时引入其他相关辅助 变量，并用 x、y 和辅助变量表示各相关量，然后根据已知条件，运用已掌握的数学知识、物理知识及其他 相关知识建立关系式，在此基础上将实际问题转化为一个函数问题，实现
5、问题数学化，即所谓建立数学模 型 第三步：利用数学的方法将得到的常规函数问题(即数学模型)予以解答，求得结果 第四步：将所得结果再转译成具体问题的解答 三、自主热身、归纳总结 1、 某商人将彩电先按原价提高 40%，然后以“八折优惠”出售，结果是每台彩电比原价多赚 270 元，那么 每台彩电原价是( ) A. 2 225 元 B. 2 250 元 C. 2 500 元 D. 3 000 元 答案 B 第 3 页 / 共 26 页 【解析】 设每台原价是 a 元，则 a(140%) 80%a270，解得 a2 250.故选 B. 2、有一批材料可以建成 200 m 的围墙，如果用此材料在一边靠墙
6、的地方围成一块矩形场地，中间用同样的 材料隔成三个面积相等的矩形(如图所示)，若围墙厚度不计，则围成的矩形最大面积为( ) 第 2 题图 A. 2 500 m2 B. 2 750 m2 C. 3 000 m2 D. 3 500 m2 【答案】 、A 【解析】 设矩形的长为 x m，宽为200 x 4 m，则 Sx 200 x 4 1 4(x 2200 x)，其中 0x200.当 x100 时，Smax2 500 m2.故选 A. 3、 将边长为 1m 的正三角形薄铁皮沿一条平行于某边的直线剪成两块，其中一块是梯形，记 S 梯形的周长2 梯形的面积 ，则 S 的最小值是_ 【答案】 、32 3
7、3 【解析】如图，设 CDx(0x1)，则 C梯形DEBAx2(1x)13x，S梯形DEBAx1 2 3 2 3 2 x 3 4 (1 x2)所以 S梯形的周长 2 梯形的面积 43x2 31x2(0x2lna2. 解：(1)f(x)的定义域为(0，)，且 f(x)xa x2 . (1.1)当 a0 时，f(x)0 成立，所以 f(x)在(0，)为增函数；(2 分) (1.2)当 a0 时， (i)当 xa 时，f(x)0，所以 f(x)在(a，)上为增函数； (ii)当 0xa 时，f(x)0 时，f(x)的最小值为 f(a)，依题意知 f(a)1lna0，解得 0aa，f(1)a0，f(x
8、)在(a，)为增函数，且函数 f(x)的图像在(a，1)上不间断 所以 f(x)在(a，)上有唯一的一个零点 另一方面， 因为 0a1 e，所以 0a 2a1 e. f(a2)1 alna 21 a2lna，令 g(a) 1 a2lna， 当 0a1 e时，g(a) 1 a2 2 a 2a1 a2 g 1 e e20 又 f(a)a2. 不妨设 x1x2，由知 0x1aa2，即证 x1a 2 x2. 因为 x1，a 2 x2(0，a)，f(x)在(0，a)上为减函数， 所以只要证 f a2 x2 f(x1) 又 f(x1)f(x2)0，即证 f a2 x2 f(x2)(14 分) 设函数 F(
9、x)f a2 x f(x)x a a x2lnx2lna(xa) 所以 F(x)（xa） 2 ax2 0，所以 F(x)在(a，)为增函数 所以 F(x2)F(a)0，所以 f a2 x2 f(x2)成立 从而 x1x2a2成立 所以 p2ln(x1x2)2lna2，即 x1f(x1)x2f(x2)2lna2 成立(16 分) 变式 1、(2019 苏州暑假测试）已知函数 f(x)x1alnx(其中 a 为参数) (1) 求函数 f(x)的单调区间； (2) 若对任意 x(0，)都有 f(x)0 成立，求实数 a 的取值集合； (3) 证明： 11 n ne0)， 当 a0 时，f(x)1a
10、x xa x 0，所以 f(x)在(0，)上是增函数；(2 分) 当 a0 时， 第 6 页 / 共 26 页 x (0，a) a (a，) f(x) 0 f(x) 极小值 所以 f(x)的增区间是(a，)，减区间是(0，a) 综上所述， 当 a0 时，f(x)的单调递增区间是(0，)； 当 a0 时，f(x)的单调递增区间是(a，)，单调递减区间是(0，a)(5 分) (2) 由题意得 f(x)min0. 当 a0 时，由(1)知 f(x)在(0，)上是增函数， 当 x0 时，f(x)，故不合题意；(6 分) 当 a0 时，由(1)知 f(x)minf(a)a1alna0.(13 分) 令
11、g(a)a1alna，则由 g(a)lna0，得 a1， a (0,1) 1 (1，) g(a) 0 g(a) 极大值 所以 g(a)a1alna0，又 f(x)minf(a)a1alna0，所以 a1alna0， 所以 a1，即实数 a 的取值集合是1(10 分) (3) 要证不等式 11 n ne11 n n1， 两边取对数后，只要证 nln11 n1(n1)ln1 1 n，(11 分) 即只要证 1 n1ln1 1 n 1 n， 令 x11 n，则只要证 1 1 xlnxx1(1f(1)，即 x1lnx0，所以 lnxx1(1x2)(14 分) 令 (x)lnx1 x1(10， 所以 (
12、x)在(1,2上递增，故 (x)(1)，即 lnx1 x10，所以 1 1 xlnx(1 1 ex 1 2 e2x成立 解 (1)函数 f(x)xln xax 的定义域为(0，) 当 a1 时，f(x)xln xx， f(x)ln x2. 由 f(x)0，得 x 1 e2. 当 x 0， 1 e2 时，f(x)0； 当 x1 e2时，f(x)0. 所以 f(x)在 0， 1 e2 上单调递减，在 1 e2， 上单调递增 因此 f(x)在 x1 e2处取得最小值，即 f(x)minf 1 e2 1 e2，但 f(x)在(0，)上无最大值 (2)证明：当 x0 时，ln x1 1 ex 1 2 e
13、2x 等价于 x(ln x1) x ex 1 2 e2. 由(1)知 a1 时，f(x)xln xx 的最小值是1 e2，当且仅当 x 1 e2时取等号 设 G(x) x ex 1 2 e2，x(0，)， 则 G(x)1x ex 1，易知 G(x)maxG(1) 1 e2， 当且仅当 x1 时取到，从而可知对一切 x(0，)，都有 f(x)G(x)，即 ln x1 1 ex 1 2 e2x. 方法总结：构造法证明不等式是指在证明与函数有关的不等式时，根据所要证明的不等式，构造与之相关 的函数， 利用函数单调性、 极值、 最值加以证明 常见的构造方法有： (1)直接构造法： 证明不等式 f(x)
14、g(x)(f(x) g(x)转化为证明 f(x)g(x)0(f(x)g(x)0)，进而构造辅助函数 h(x)f(x)g(x)；(2)适当放缩构造法：一 是根据已知条件适当放缩，二是利用常见的放缩结论，如 ln xx1，exx1，ln xxex(x0)， x x1ln(x 1)x(x1)；(3)构造“形似”函数：稍作变形再构造，对原不等式同解变形，如移项、通分、取对数，把 不等式转化为左、右两边是相同结构的式子的形式，根据“相同结构”构造辅助函数；(4)构造双函数：若直 接构造函数求导难以判断符号，导函数零点也不易求得，因此函数单调性与极值点都不易获得，则可构造 函数 f(x)和 g(x)，利用
15、其最值求解 考点二、利用导数研究恒成立问题 第 8 页 / 共 26 页 例 2、 （2018 年南通一模）已知函数 f(x) |x32x2x|， x1， lnx， x1， 若对于tR，f(t)kt 恒成立，则实数 k 的取值范围是_ 答案： 1 e，1 思路分析 本题条件“tR，f(t)kt”的几何意义是：在(，)上，函数 yf(t)的图像恒 在直线 ykt 的下方，这自然提示我们利用数形结合的方法解决本问题 令 yx32x2x，x0，即(x1)(3x1)0，解得 x1.又因为 x1，所以 x1 3.令 y0，得 1 3x1，所以 y 的增区间是(， 1 3)，减区间是( 1 3，1)，所以
16、 y 极大值 4 27. 根据图像变换可作出函数 y|x32x2x|，x1 的图像又设函数 ylnx(x1)的图像经过原点的切线斜率 为 k1，切点(x1，lnx1)，因为 y1 x，所以 k1 1 x1 lnx10 x10 ，解得 x1e，所以 k11 e.函数 yx 32x2x 在原 点处的切线斜率 k2yx01.因为tR，f(t)kt，所以根据 f(x)的图像，数形结合可得1 ek1. 变式 1、(2018 无锡期末）已知函数 f(x)ex(3x2)，g(x)a(x2)，其中 a，xR. (1) 求过点(2，0)和函数 yf(x)图像相切的直线方程； (2) 若对任意 xR，有 f(x)
17、g(x)恒成立，求 a 的取值范围； (3) 若存在唯一的整数 x0，使得 f(x0)g(x0)，求 a 的取值范围 思路分析 (1)利用导数的几何意义求切线的方程，根据斜率建立方程即可 (2)不等式恒成立问题处理的方法有两种：一种是分离参变，转化为相应函数的值域(最值)问题解决；另 一种是转化为含参函数的值域问题，通过分类讨论解决这里可以采取第一种方法，只是分离参变时要注 意对 x2 的符号进行分类讨论 (3)在第(2)小问的基础上，分离参变，转化为存在有限整数自变量满足条件的问题利用导数研究函数 F(x)e x（3x2） x2 的性质，找到相关的整数自变量，求得对应的函数值是解决本问题的关
18、键 规范解答 (1) 设切点为(x0，y0)，f(x)ex(3x1)，则切线斜率为 ex0(3x01)，所以切线方程为 yy0 ex0(3x01)(xx0)，因为切线过点(2，0)， 所以ex0(3x02)ex0(3x01)(2x0)， 第 9 页 / 共 26 页 化简得 3x208x00，解得 x00 或 x08 3，(3 分) 当 x00 时，切线方程为 yx2，(4 分) 当 x08 3时，切线方程为 y9e 8 3x18e 8 3.(5 分) (2) 由题意，对任意 xR，有 ex(3x2)a(x2)恒成立， 当 x(，2)时，ae x（3x2） x2 ，即 a ex（3x2） x2
19、 max. 令 F(x)e x（3x2） x2 ，则 F(x)e x（3x28x） （x2）2 ， 令 F(x)0，得 x0，列表如下： x (，0) 0 (0，2) F(x) 0 F(x) 极大 F(x)maxF(0)1，故此时 a1.(7 分) 当 x2 时，恒成立，故此时 aR.(8 分) 当 x(2，)时，ae x（3x2） x2 ，即 a ex（3x2） x2 min，令 F(x)0，得 x 8 3，列表如下： x 2，8 3 8 3 8 3， F(x) 0 F(x) 极小 F(x)minF 8 3 9e8 3， 故此时 a9e 8 3，综上，1a9e 8 3.(10 分) (3)
20、由 f(x)g(x)，得 ex(3x2)a(x2)， 由(2)知 a(，1)(9e8 3，)， 令 F(x)e x（3x2） x2 ，列表如下： x (，0) 0 (0，2) 2，8 3 8 3 8 3， F(x) 0 0 F(x) 极大 极小 (12 分) 当 x(，2)时，存在唯一的整数 x0使得 f(x0)g(x0)， 第 10 页 / 共 26 页 等价于 ae x（3x2） x2 存在的唯一整数 x0成立， 因为 F(0)1 最大， F(1) 5 3e， F(1)e， 所以当 a 5 3e时， 至少有两个整数成立， 所以 a 5 3e，1 .(14 分) 当 x(2，)时，存在唯一的
21、整数 x0使得 f(x0)e x（3x2） x2 存在唯一的整数 x0成立， 因为 F 8 3 9e8 3最小，且 F(3)7e 3，F(4)5e4，所以当 a5e4 时，至少有两个整数成立，当 a7e3时， 没有整数成立，所以 a(7e3，5e4 综上，a 5 3e，1 (7e 3，5e4(16 分) 变式 2、(2019 广东汕头二模)已知函数 f(x)aln xx1(其中 aR) (1)讨论函数 f(x)的极值； (2)对任意 x0，f(x)1 2(a 21)成立，求实数 a 的取值范围 解：(1)f(x)的定义域为(0，)，f(x)a x1. 当 a0 时，在(0，)上，f(x)0 时
22、，令 f(x)0，得 xa， 在(0，a)上，f(x)0，f(x)是增函数；在(a，)上，f(x)0 时，f(x)有极大值 f(a)aln aa1，无极小值 (2)由(1)知当 a0，f(x)是减函数， 令 be a 2，b1，则 ln b0，不成立 当 a0 时，当 xa 时，f(x)取得极大值也是最大值， 所以 f(x)maxf(a)aln aa1， 要使得对任意 x0，f(x)1 2(a 21)成立， 即 aln aa11 2(a 21)， 第 11 页 / 共 26 页 则 aln a3 2a 1 2a 20 成立， 令 u(a)aln a3 2a 1 2a 2(a0)， 所以 u(a
23、)ln a11aln aa， 令 k(a)u(a)ln aa， k(a)1 a1，令 k(a) 1a a 0，得 a1， 在(0,1)上，k(a)0，k(a)u(a)是增函数，在(1，)上，k(a)0，k(a)u(a)是减函数， 所以当 a1 时，k(a)u(a)取得极大值也是最大值， u(a)maxu(1)10， 在(0，)上，u(a)0)，则 F(x)x1 x (x0)， 当 0x1 时，F(x)1 时，F(x)0，F(x)单调递增 F(x)F(1)10，a x202x0 x0ln x0. 记 G(x)x 22x xln x，x 1 e，e ， 则 G(x)2x2xln xx2x1 xln
24、 x2 第 12 页 / 共 26 页 x1x2ln x2 xln x2 . x 1 e，e ， 22ln x2(1ln x)0， x2ln x20， 当 x 1 e，1 时，G(x)0，G(x)单调递增 G(x)minG(1)1， aG(x)min1， 故实数 a 的取值范围为1，) 方法总结：分离参数法解含参不等式恒成立问题的思路与关键 (1)分离参数法解含参不等式恒成立问题的思路 用分离参数法解含参不等式恒成立问题是指在能够判断出参数的系数的正负的情况下，可以根据不等 式的性质将参数分离出来，得到一个一端是参数，另一端是变量表达式的不等式，只要研究变量表达式的 最值就可以解决问题 (2)
25、求解含参不等式恒成立问题的关键是过好“双关” 考点三、利用导数研究函数零点问题 例 3、(2019 通州、海门、启东期末）已知函数 f(x)x2alnx1，aR. (1) 当 a2 时，求函数 f(x)的极值； (2) 若函数 f(x)有两个零点，求实数 a 的取值范围 .思路分析 第 2 问，注意到 f(1)0，因此，函数 f(x)已经有一个零点 1，为此，就需要考虑它有另一个 零点，据此，通过研究函数的单调性及单调区间来确定每个单调区间上的零点的个数由于 f(x)2x 2a x ， 下面就要考虑方程 2x2a0 在(0， )上是否有实数根， 实数根是否等于 1， 为此， 得到分类讨论的标准
26、， 即 a0，0a2，分别来讨论每种情形时函数 f(x)的零点的个数，从而得到实数 a 的取值范围 (1)当 a2 时，f(x)2x2 x，令 f(x)0，解得 x1.(2 分) 列表： x (0，1) 1 (1，) f(x) 0 第 13 页 / 共 26 页 f(x) 极小值 f(1) 所以，当 x1 时，f(x)有极小值 f(1)0，f(x)没有极大值(4 分) (2)因为 f(x)x2alnx1，x0.所以 f(1)0，f(x)2xa x. 当 a0 时，f(x)0. 所以 f(x)在(0，)上单调递增，f(x)只有一个零点，不合题意(6 分) 当 a0 时，由 f(x)0 得 x a
27、 2，由 f(x)0 得 xx a 2， 所以 f(x)在 0， a 2 上单调递减，f(x)在 a 2， 上单调递增， 所以 f(x)在 x a 2处取得极小值，即为最小值 1 当 a2 时，f(x)在(0，1)上单调递减，f(x)在(1，)上单调递增，f(x)只有一个零点，不合题意：(8 分) 2 当 0a2 时， a 21，故 f a 2 alnx1，令alnx10， 取 x0e x 1 ，使得 f(x0)0，下面先证明 a 2e x 1 ； 设 g(x)xlnx，g(x)lnx1，令 g(x)0，解得 x1 e. 列表： x 0，1 e 1 e 1 e， g(x) 0 g(x) 极小值
28、 g 1 e 所以，当 x1 e时，g(x)有极小值 g 1 e 1 e. 所以 xlnx1 e1，故 a 2ln a 21，即 a 2e x 1 因此，根据零点存在性定理知，在 e1 a， a 2 上 f(x)必存在一个零点， 又 x1 也是 f(x)的一个零点，则 f(x)有两个相异的零点，符合题意(12 分) 3 当 a2 时， a 21，故 f a 2 f(1)0，f(x)最多有两个零点 注意到 lnx a 2. 第 14 页 / 共 26 页 则 f(x)x2lnx1(a1)2aln(a1)1(a1)2a(a1)1a0， 因此，根据零点存在性定理知，在 a 2，a1 上 f(x)必存
29、在一个零点， 又 x1 也是 f(x)的一个零点，则 f(x)有两个相异的零点，符合题意 综上所述，实数 a 的取值范围是(0，2)(2，)(16 分) 变式 1、(2019 南通一调）已知函数 f(x)ax2xlnx，aR. (1) 当 a3 8时，求函数 f(x)的最小值； (2) 若1a0，证明：函数 f(x)有且只有一个零点； (3) 若函数 f(x)有两个零点，求实数 a 的取值范围 规范解答 (1) 当 a3 8时，f(x) 3 8x 2xlnx. 故 f(x)3 4x1 1 x 3x2x2 4x ，x0.(2 分) 令 f(x)0，得 x2， 当 x(0,2)时，f(x)0；当
30、x(2，)时，f(x)0， 所以函数 f(x)在(0,2)上单调递减，在(2，)上单调递增 所以当 x2 时，f(x)有最小值 f(2)1 2ln2.(4 分) (2) 由 f(x)ax2xlnx，得 f(x)2ax11 x 2ax2x1 x ，x0. 所以当 a0 时，f(x)2ax 2x1 x 0， 函数 f(x)在(0，)上单调递减， 所以当 a0 时，函数 f(x)在(0，)上最多有一个零点(6 分) 因为当1a0 时，f(1)a10，f 1 e e 2ea e2 0， 所以当1a0 时，函数 f(x)在(0，)上有零点 综上，当1a0 时，函数 f(x)有且只有一个零点(8 分) (
31、3) 解法 1 由(2)知，当 a0 时，函数 f(x)在(0，)上最多有一个零点 因为函数 f(x)有两个零点，所以 a0.(9 分) 由 f(x)ax2xlnx，得 f(x)2ax 2x1 x ，x0，令 g(x)2ax2x1. 因为 g(0)10,2a0， 所以函数 g(x)在(0，)上只有一个零点，设为 x0. 第 15 页 / 共 26 页 当 x(0，x0)时，g(x)0，f(x)0；当 x(x0，)时，g(x)0，f(x)0. 所以函数 f(x)在(0，x0)上单调递减；在(x0，)上单调递增 要使得函数 f(x)在(0，)上有两个零点， 只需要函数 f(x)的极小值 f(x0)
32、0，即 ax20 x0lnx00. 又因为 g(x0)2ax20 x010，所以 2lnx0 x010. 又因为函数 h(x)2lnxx1 在(0，)上是增函数，且 h(1)0，所以 x01，得 01 x01. 又由 2ax20 x010，得 2a 1 x0 21 x0 1 x0 1 2 21 4，所以 0a1.(13 分) 以下验证当 0a1 时，函数 f(x)有两个零点 当 0a1 时，g 1 a 2a a2 1 a1 1a a 0， 所以 1x01 a. 因为 f 1 e a e2 1 e1 e2ea e2 0，且 f(x0)0. 所以函数 f(x)在 1 e，x0 上有一个零点 又因为
33、 f 2 a 4a a2 2 aln 2 a 2 a 2 a1 10(因为 lnxx1)，且 f(x0)0. 所以函数 f(x)在 x0，2 a 上有一个零点 所以当 0a1 时，函数 f(x)在 1 e， 2 a 内有两个零点 综上，实数 a 的取值范围为(0,1)(16 分) 下面证明：lnxx1. 设 t(x)x1lnx，所以 t(x)11 x x1 x (x0) 令 t(x)0，得 x1. 当 x(0,1)时，t(x)0；当 x(1，)时，t(x)0. 所以函数 t(x)在(0,1)上单调递减，在(1，)上单调递增 所以当 x1 时，t(x)有最小值 t(1)0. 所以 t(x)x1l
34、nx0，得 lnxx1 成立 解法 2 由(2)知，当 a0 时，函数 f(x)在(0，)上最多有一个零点 因为函数 f(x)有两个零点，所以 a0.(9 分) 第 16 页 / 共 26 页 由 f(x)ax2xlnx0，得关于 x 的方程 axlnx x2 ，x0，有两个不等的实数解 又因为 lnxx1， 所以 axlnx x2 2x1 x2 1 x1 21，x0. 因为 x0 时， 1 x1 211，所以 a1. 又当 a1 时，x1，即关于 x 的方程 axlnx x2 有且只有一个实数解 所以 0a1.(13 分) (以下解法同解法 1) 变式 2、设函数 f(x)(x1)exk 2
35、x 2. (1)当 k0，解得 x0，令 f(x)0，解得 x0，所以 f(x)的单调递减区间是(，0)，单调递增 区间是(0，) 当 0k0，解得 x0，令 f(x)0，解得 ln kx0， 所以 f(x)在(，ln k)和(0，)上单调递增，在(ln k,0)上单调递减 (2)f(0)1.当 k0，又 f(x)在0，)上单调递增，所以函数 f(x)在0，)上只有 一个零点 在区间(， 0)上， f(x)(x1)exk 2x 2x1k 2x 2， 取 x2 k1， 可得 f 2 k1 2 k1 1 k 2 2 k1 2k 20，又 f(x)在(，0)上单调递减，所以 f(x)在(，0)上也只
36、有一个零点 所以函数 f(x)在定义域(，)上有两个零点 当 k0 时，f(x)(x1)ex，f(x)xex.易知 f(x)在(，0)上单调递减，在0，)上单调递增，又 f(1) 0，所以 f(x)在0，)上只有一个零点因为 x(，0)时，x10，所以 f(x)0，即 f(x)在区间 (，0)上无零点所以函数 f(x)在定义域(，)上只有一个零点. 方法总结：(1)分离参数法：一般命题情境为给出区间，求满足函数零点个数的参数范围，通常解法为从 f(x) 中分离出参数，然后利用求导的方法求出由参数构造的新函数的最值，根据题设条件构建关于参数的不等 式，再通过解不等式确定参数范围；(2)分类讨论法
37、：一般命题情境为没有固定区间，求满足函数零点个数 第 17 页 / 共 26 页 的参数范围，通常解法为结合单调性，先确定参数分类的标准，在每个小范围内研究零点的个数是否符合 题意，将满足题意的参数的各小范围并在一起，即为所求参数范围. 考点四、运用导数解决实际问题 例 4、(2019 南京、盐城一模）盐城市政府响应习总书记在十九大报告中提出的“绿水青山就是金山银山”， 对环境进行了大力整治，目前盐城市的空气质量位列全国前十，吸引了大量的外地游客某旅行社组织了 一个旅游团于近期来到了黄海国家森林公园，数据显示，近期公园中每天空气质量指数近似满足函数 f(x) mlnxx 600 x x2144
38、6(4x22，mR)，其中 x 为每天的时刻，若凌晨 6 点时，测得空气质量指数为 29.6. (1) 求实数 m 的值； (2) 求近期每天时段空气质量指数最高的时刻(参考数值：ln61.8) 思路分析 第(2)问，导函数 f(x)m x1600 144x2 （x2144）2的代数变形成为本题的难点，发现公因式 12 x 是解决本题的关键 规范解答 (1)由 f(6)29.6，代入 f(x)mlnxx 600 x x21446(4x22，mR)，解得 m12.(5 分) (2)由已知函数求导，得 f(x)12x x 600 144x2 （x2144）2(12x 令 f(x)0，得 x12.(
39、9 分) 列表得 x 4，12) 12 (12，22 f(x) 0 f(x) 极大值 所以函数在 x12 时取极大值也是最大值，即每天时段空气质量指数最高的时刻为 12 时. (12 分) 答：(1)实数 m 的值为 12；(2)空气质量指数最高的时刻为 12 时(14 分) 解后反思 本题第(2)问，因为部分学生不能发现导函数中有公因式 12x，导致二次求导，但是没有交 代清楚，导致失分. 当然本题可以分别求函数 y12lnxx 和函数 y 600 x x21446 的最大值，并交代在 x 12 处同时取得最大值即可在评分细则中，第(2)问若不列表或文字说明单调性的扣 3 分；最后未给出“答
40、” 再扣 2 分. 变式 1、一栋新农村别墅，它由上部屋顶和下部主体两部分组成如图，屋顶由四坡屋面构成，其中前后 第 18 页 / 共 26 页 两坡屋面ABFE和CDEF是全等的等腰梯形， 左右两坡屋面EAD和FBC是全等的三角形 点F在平面ABCD 和 BC 上的射影分别为 H，M.已知 HM5 m，BC10 m，梯形 ABFE 的面积是FBC 面积的 2.2 倍设 FMH 0 4 . (1) 求屋顶面积 S 关于 的函数关系式； (2) 已知上部屋顶造价与屋顶面积成正比， 比例系数为 k(k 为正的常数)， 下部主体造价与其高度成正比， 比例系数为 16k.现欲造一栋上、下总高度为 6
41、m 的别墅，试问：当 为何值时，总造价最低？ ,) (1)先通过线面垂直得到 FHHM，放在 RtFHM 中，求出 FM，根据三角形的面积公式求出FBC 的 面积，根据已知条件就可以得到所求 S 关于 的函数关系式 (2)先求出主体高度，进而建立出别墅总造价 y 关于 的函数关系式，再通过导数法求函数的最小值 (1)规范解答 由题意 FH平面 ABCD，FMBC，又因为 HM平面 ABCD，得 FHHM.(2 分) 在 RtFHM 中，HM5，FMH， 所以 FM 5 cos.(4 分) 因此FBC 的面积为1 2 10 5 cos 25 cos. 从而屋顶面积 S2S FBC 2S梯形ABF
42、E2 25 cos2 25 cos 2.2 160 cos. 所以 S 关于 的函数关系式为 S 160 cos 0 4 .(6 分) (2)在 RtFHM 中，FH5tan，所以主体高度为 h65tan.(8 分) 所以别墅总造价为 yS kh 16k 160 cosk 80sin cos k96k80k 2sin cos 96k.(10 分) 记 f()2sin cos ，0 4，所以 f() 2sin1 cos2 ， 令 f()0，得 sin1 2，又 0 4，所以 6.(12 分) 列表： 0， 6 6 6， 4 f() 0 f() 3 第 19 页 / 共 26 页 所以当 6时，f
43、()有最小值 答：当 为 6时，该别墅总造价最低(14 分) 解后反思 理解题意，建立出函数的关系式，是处理最优解类型应用问题的关键，第(1)问，抓住条件” 梯形 ABFE 的面积是FBC 面积的 2.2 倍”，只要用 表示出FBC 面积，即可得到屋顶面积第(2)问，需 要先设出总造价为 y 元，抓住已知条件，求出主体高度并结合第(1)问中求得的屋顶面积，就可以建立函数 关系式 变式 2、提高过江大桥的车辆通行能力可改善整个城市的交通状况在一般情况下，大桥上的车流速度 v(单 位：千米/小时)是车流密度 x(单位：辆/千米)的函数当桥上的车流密度达到 200 辆/千米时，造成堵塞，此 时车流速
44、度为0千米/小时； 当车流密度不超过20辆/千米时， 车流速度为60千米/小时， 研究表明： 当20 x200 时，车流速度 v 是车流密度 x 的一次函数 (1)当 0 x200 时，求函数 v(x)的表达式； (2)当车流密度 x 为多大时， 车流量(单位时间内通过桥上某观测点的车辆数， 单位： 辆/小时)f(x)x v(x) 可以达到最大，并求出最大值(精确到 1 辆/小时) 【解】 (1)由题意可知当 0 x20 时，v(x)60；当 20 x200 时，设 v(x)axb，显然 v(x)axb 在20，200上是减函数，由已知得 200ab0， 20ab0， 解得 a 1 3， b2
45、00 3 ， 故函数 v(x)的表达式为 v(x) 60，0 x20， 1 3（200 x），20 x200. (2)依题意并由(1)可得 f(x) 60 x，0 x20， 1 3x（200 x），20 x200. 当 0 x20 时，f(x)为增函数，故当 x20 时，其最大值为 60 201 200； 当 20 x200 时，f(x)1 3x(200 x) 1 3 x（200 x） 2 210 000 3 ，当且仅当 x200 x，即 x100 时， 等号成立， 当 x100 时，f(x)在区间20，200上取得最大值10 000 3 . 综上，当 x100 时，f(x)在区间0，200上
46、取得最大值10 000 3 3 333，即当车流密度为 100 辆/千米时， 第 20 页 / 共 26 页 车流量可以达到最大，最大值约 3 333 辆/小时 方法总结：构建数学模型解决实际问题，要正确理解题意，分清条件和结论，理顺数量关系，将文字语言 转化成数学语言，建立适当的函数模型，然后再根据函数模型的类型和特征，结合对函数的图像和性质的 研究获得结果求解过程中不要忽略实际问题对变量的限制 五、优化提升与真题演练 1、 （2019 年高考天津理数） 已知aR， 设函数 2 22 ,1, ( ) ln ,1. xaxax f x xaxx 若关于x的不等式( )0f x 在R上恒成立，则
47、a的取值范围为 A0,1 B0,2 C0,e D1,e 【答案】C 【解析】当1x 时，(1)1 2210faa 恒成立； 当1x时， 2 2 ( )2202 1 x f xxaxaa x 恒成立， 令 2 ( ) 1 x g x x ， 则 222 (11)(1)2(1) 1 ( ) 111 xxxx g x xxx 11 122 (1)20 11 xx xx ， 当 1 1 1 x x ，即0 x时取等号， max 2( )0ag x，则0a. 当1x 时，( )ln0f xxax，即 ln x a x 恒成立， 令( ) ln x h x x ，则 2 ln1 ( ) (ln ) x h x x ， 第 21 页 / 共 26 页 当ex时，( )0h x ，函数( )h x单调递增， 当0ex时，( )0h x ，函数( )h x单调递减， 则ex
