1、2019-2020 学年四川省成都市学年四川省成都市郫都区郫都区高三（上）高三（上）9 月月考数学试卷（文科）月月考数学试卷（文科） 一、选择題（每小题一、选择題（每小题 5 分，共分，共 60 分）分） 1 （5 分）已知集合 Ax|x22，则RA（ ） Ax|2x2 Bx|x2 或 x2 C D 2 （5 分）若 z（1+i）2i，则 z（ ） A1i B1+i C1i D1+i 3 （5 分）设 ， 为非零向量，则“”是“ 与 方向相同”的（ ） A充分而不必要条件 B必要而不充分条件 C充分必要条件 D既不充分也不必要条件 4 （5 分）函数 f（x）x+lnx3 的零点位于区间（ ）
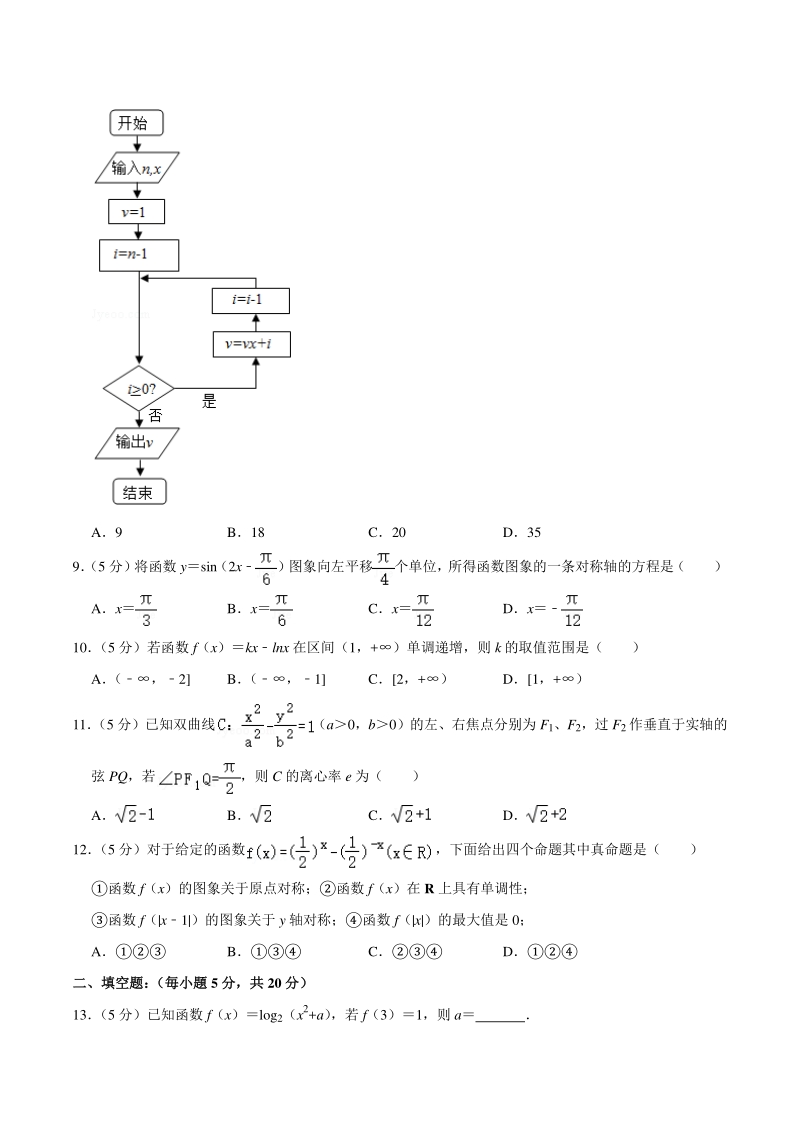
2、 A （0，1） B （1，2） C （2，3） D （3，4） 5 （5 分）已知，则 cos2（ ） A B C D 6 （5 分）函数 f（x）xln|x|的图象可能是（ ） A B C D 7 （5 分）已知向量 ， 满足，且，则向量 与 的夹角的余弦值为（ ） A B C D 8 （5 分）秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的数书九章中提出 的多项式求值的秦九韶算法，至今仍是比较先进的算法如图所示的程序框图给出了利用秦九韶算法求 某多项式值的一个实例，若输入 n，x 的值分别为 3，2，则输出 v 的值为（ ） A9 B18 C20 D35 9 （5 分
3、）将函数 ysin（2x）图象向左平移个单位，所得函数图象的一条对称轴的方程是（ ） Ax Bx Cx Dx 10 （5 分）若函数 f（x）kxlnx 在区间（1，+）单调递增，则 k 的取值范围是（ ） A （，2 B （，1 C2，+） D1，+） 11 （5 分）已知双曲线（a0，b0）的左、右焦点分别为 F1、F2，过 F2作垂直于实轴的 弦 PQ，若，则 C 的离心率 e 为（ ） A B C D 12 （5 分）对于给定的函数，下面给出四个命题其中真命题是（ ） 函数 f（x）的图象关于原点对称；函数 f（x）在 R 上具有单调性； 函数 f（|x1|）的图象关于 y 轴对称；函
4、数 f（|x|）的最大值是 0； A B C D 二、填空题： （毎小題二、填空题： （毎小題 5 分，共分，共 20 分）分） 13 （5 分）已知函数 f（x）log2（x2+a） ，若 f（3）1，则 a 14 （5 分）若变量 x、y 满足约束条件，则 zx+2y 的最大值为 15 （5 分）等比数列an的各项均为实数，其前 n 项和为 Sn，已知 S3，S6，则 a8 16 （5 分）已知球的直径 DC4，A、B 是该球面上的两点，则三棱锥 ABCD 的体 积最大值是 三、解答題， （本大题共三、解答題， （本大题共 6 小题，共小题，共 70 分）分） 17 （12 分）在ABC
5、中，内角 A，B，C 所对的边分别为 a，b，c，已知 asin2BbsinA （1）求 B； （2）已知 cosA，求 sinC 的值 18 （12 分）某家电公司销售部门共有 200 位销售员，每位部门对每位销售员都有 1400 万元的年度销售任 务，已知这 200 位销售员去年完成销售额都在区间2，22（单位：百万元）内，现将其分成 5 组，第 1 组，第 2 组，第 3 组，第 4 组，第 5 组对应的区间分别为2，6） ，6，10） ，10，14） ，14，18） ，18， 22，绘制出频率分布直方图 （1）求 a 的值，并计算完成年度任务的人数； （2）用分层抽样从这 200 位销
6、售员中抽取容量为 25 的样本，求这 5 组分别应抽取的人数； （3）现从（2）中完成年度任务的销售员中随机选取 2 位，奖励海南三亚三日游，求获得此奖励的 2 位 销售员在同一组的概率 19（12 分） 如图， 在四棱锥 PABCD 中， ABCACD90， BACCAD60， PA平面 ABCD， PA2，AB1设 M，N 分别为 PD，AD 的中点 （1）求证：平面 CMN平面 PAB； （2）求三棱锥 PABM 的体积 20 （12 分）在平面直角坐标系 xOy 中，已知椭圆 C 的中心在原点 O，焦点在 x 轴上，短轴长为 2，离心率 为，过左顶点 A 的直线 l 与椭圆交于另一点
7、B （）求椭圆 C 的方程； （）若|AB|，求直线 l 的倾斜角 21 （12 分）设函数 f（x）2lnxx2+ax+2 （）当 a3 时，求 f（x）的单调区间和极值； （）若直线 yx+1 是曲线 yf（x）的切线，求 a 的值 22 （10 分）以平面直角坐标系的原点为极点，x 轴的正半轴为极轴，建立极坐标系，已知直线 l 的参数方 程是（m0，t 为参数） ，曲线 C 的极坐标方程为 2cos （）求直线 l 的普通方程和曲线 C 的直角坐标方程； （）若直线 l 与 x 轴交于点 P，与曲线 C 交于点 A，B，且|PA|PB|1，求实数 m 的值 参考答案与试题解析参考答案与试
8、题解析 一、选择題（每小题一、选择題（每小题 5 分，共分，共 60 分）分） 1 （5 分）已知集合 Ax|x22，则RA（ ） Ax|2x2 Bx|x2 或 x2 C D 【分析】利用补集的定义，判断 A 集合，求解即可 【解答】解：已知集合 Ax|x22，解得：， 所以RAx|x或 x 故选：D 【点评】本题考查集合补集运算，考查运算求解能力 2 （5 分）若 z（1+i）2i，则 z（ ） A1i B1+i C1i D1+i 【分析】利用复数的运算法则求解即可 【解答】解：由 z（1+i）2i，得 z 1+i 故选：D 【点评】本题主要考查两个复数代数形式的乘法和除法法则，虚数单位 i
9、 的幂运算性质，属于基础题 3 （5 分）设 ， 为非零向量，则“”是“ 与 方向相同”的（ ） A充分而不必要条件 B必要而不充分条件 C充分必要条件 D既不充分也不必要条件 【分析】由充分条件、必要条件的判定方法及向量共线的概念分析得答案 【解答】解：对于非零向量 ， ，由 与 方向相同或相反， 反之， 与 方向相同， 则“”是“ 与 方向相同”的必要而不充分条件 故选：B 【点评】本题考查充分条件、必要条件的判定方法，考查向量共线的概念，是基础题 4 （5 分）函数 f（x）x+lnx3 的零点位于区间（ ） A （0，1） B （1，2） C （2，3） D （3，4） 【分析】对 f
10、（x）进行求导，得到其单调性，再利用零点定理进行判断； 【解答】解：函数 f（x）x+lnx3， （x0） f（x）1+，可得 f（x）0，f（x）为增函数， f（1）1+0320， f（2）2+ln23ln210， f（3）3+ln33ln30， f（2）f（3）0， 所以 f（x）的零点所在区间为（2，3） ， 故选：C 【点评】此题主要考查函数零点的判定定理，此题主要函数的定义域 x0，此题是一道基础题； 5 （5 分）已知，则 cos2（ ） A B C D 【分析】由已知求得 sin，再由二倍角的余弦求解 【解答】解：由，得 sin， cos2 故选：B 【点评】本题考查三角函数的化
11、简求值，考查倍角公式的应用，是基础题 6 （5 分）函数 f（x）xln|x|的图象可能是（ ） A B C D 【分析】判断函数的奇偶性排除选项，利用特殊点的位置排除选项即可 【解答】解：函数 f（x）xln|x|是奇函数，排除选项 A，C； 当 x时，y，对应点在 x 轴下方，排除 B； 故选：D 【点评】本题考查函数的图象的判断，函数的奇偶性以及特殊点的位置是判断函数的图象的常用方法 7 （5 分）已知向量 ， 满足，且，则向量 与 的夹角的余弦值为（ ） A B C D 【分析】利用已知条件，结合斜率的数量积转化求解向量 与 的夹角的余弦值 【解答】解：由题意可知，且，可得 3+24，
12、解得， 向量 与 的夹角的余弦值： 故选：D 【点评】本题考查平面向量的数量积运算，考查运算求解能力 8 （5 分）秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的数书九章中提出 的多项式求值的秦九韶算法，至今仍是比较先进的算法如图所示的程序框图给出了利用秦九韶算法求 某多项式值的一个实例，若输入 n，x 的值分别为 3，2，则输出 v 的值为（ ） A9 B18 C20 D35 【分析】 由题意， 模拟程序的运行， 依次写出每次循环得到的 i， v 的值， 当 i1 时， 不满足条件 i0， 跳出循环，输出 v 的值为 18 【解答】解：初始值 n3，x2，程序运行过程如下
13、表所示： v1 i2 v12+24 i1 v42+19 i0 v92+018 i1 跳出循环，输出 v 的值为 18 故选：B 【点评】本题主要考查了循环结构的程序框图的应用，正确依次写出每次循环得到的 i，v 的值是解题的 关键，属于基础题 9 （5 分）将函数 ysin（2x）图象向左平移个单位，所得函数图象的一条对称轴的方程是（ ） Ax Bx Cx Dx 【分析】由条件利用 yAsin（x+）的图象变换规律，正弦函数的图象的对称性，得出结论 【解答】解：将函数 ysin（2x）图象向左平移个单位， 所得函数图象对应的函数的解析式为 ysin2（x+）sin（2x+） ， 当 x时，函数
14、取得最大值，可得所得函数图象的一条对称轴的方程是 x， 故选：C 【点评】本题主要考查 yAsin（x+）的图象变换规律，正弦函数的图象的对称性，属于基础题 10 （5 分）若函数 f（x）kxlnx 在区间（1，+）单调递增，则 k 的取值范围是（ ） A （，2 B （，1 C2，+） D1，+） 【分析】求出导函数 f（x） ，由于函数 f（x）kxlnx 在区间（1，+）单调递增，可得 f（x）0 在区间（1，+）上恒成立解出即可 【解答】解：f（x）k， 函数 f（x）kxlnx 在区间（1，+）单调递增， f（x）0 在区间（1，+）上恒成立 k， 而 y在区间（1，+）上单调递减
15、， k1 k 的取值范围是：1，+） 故选：D 【点评】本题考查了利用导数研究函数的单调性、恒成立问题的等价转化方法，属于中档题 11 （5 分）已知双曲线（a0，b0）的左、右焦点分别为 F1、F2，过 F2作垂直于实轴的 弦 PQ，若，则 C 的离心率 e 为（ ） A B C D 【分析】首先根据已知条件建立等量关系，进一步利用通径和焦距间的等量求出双曲线的离心率 【解答】解：双曲线的左右焦点分别为 F1、F2，过 F2作垂直于实轴的弦 PQ，若， 则：F1PQ 为等腰直角三角形 由于通径 PQ， 则：2c， 解得：c2a22ac0， 所以：e22e10， 解得：e1； 由于 e1， 所
16、以：e1+， 故选：C 【点评】本题考查的知识要点：通径在求离心率中的应用，等腰直角三角形的性质的应用属于基础题 型 12 （5 分）对于给定的函数，下面给出四个命题其中真命题是（ ） 函数 f（x）的图象关于原点对称；函数 f（x）在 R 上具有单调性； 函数 f（|x1|）的图象关于 y 轴对称；函数 f（|x|）的最大值是 0； A B C D 【分析】根据奇函数的定义进行判断； 根据函数单调性的性质进行判断； 根据偶函数的定义进行判断； 根据函数单调性和最值关系进行判断 【解答】解：f（x）（） x（ ）x（）x（） xf（x） ， 则函数 f（x）是奇函数，则函数 f（x）的图象关于
17、原点对称；故正确， ）f（x）（）x（） x（ ）x2x为减函数，故函数 f（x）在 R 上具有单调性；故正确， f（|x1|）（）|x 1|（ ） |x1|， 则设 g（x）f（|x1|）（）|x 1|（ ） |x1|， 则 g（x）（）| x1|（ ） |x1|（ ）|x+1|（） |x+1|， 则 g（x）g（x） ，则 g（x）不是偶函数，则函数 f（|x1）|的图象关于 y 轴不对称；故错误， 函数 f（|x|）（）|x|（） |x|，为偶函数，且当 x0 时为减函数， 故当 x0 时，函数取得最大值，最大值为 f（|0|）（）0（） 0110，故正确， 故正确的是， 故选：D 【点
18、评】本题主要考查命题的真假判断，涉及函数奇偶性好的大小的判断和应用，以及函数最值和单调 性的关系，综合性较强，有一定的难度 二、填空题： （毎小題二、填空题： （毎小題 5 分，共分，共 20 分）分） 13 （5 分）已知函数 f（x）log2（x2+a） ，若 f（3）1，则 a 7 【分析】直接利用函数的解析式，求解函数值即可 【解答】解：函数 f（x）log2（x2+a） ，若 f（3）1， 可得：log2（9+a）1，可得 a7 故答案为：7 【点评】本题考查函数的解析式的应用，函数的零点与方程根的关系，是基本知识的考查 14 （5 分）若变量 x、y 满足约束条件，则 zx+2y
19、的最大值为 8 【分析】先根据约束条件画出可行域，再利用几何意义求最值，只需求出直线 zx+2y 过点 A（4，2） 时，z 最大值即可 【解答】解：作出可行域如图， 由 zx+2y 知，yx+z， 所以动直线 yx+z 的纵截距 z 取得最大值时， 目标函数取得最大值 由得 A（4，2） 结合可行域可知当动直线经过点 A（4，2）时， 目标函数取得最大值 z4+228 故答案为：8 【点评】本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题 15 （5 分）等比数列an的各项均为实数，其前 n 项和为 Sn，已知 S3，S6，则 a8 32 【分析】设等比数列an的公比为 q1
20、，S3，S6，可得， 联立解出即可得出 【解答】解：设等比数列an的公比为 q1， S3，S6， 解得 a1，q2 则 a832 故答案为：32 【点评】本题考查了等比数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题 16 （5 分）已知球的直径 DC4，A、B 是该球面上的两点，则三棱锥 ABCD 的体 积最大值是 2 【分析】由题意画出图形，可知要使 VABCD的体积最大，则面 ADC面 BDC，求出 A 到平面 BCD 的 距离，则三棱锥 ABCD 的体积最大值可求 【解答】解：如图， 球的直径 DC4，且， ACBC2，（其中 h 为点 A 到底面 BCD 的距离） ，
21、故当 h 最大时，VABCD的体积最大，即当面 ADC面 BDC 时，h 最大且满足，即 h， 此时 VABCD 故答案为：2 【点评】本题考查球内接多面体体积的求法，考查空间想象能力与思维能力，是中档题 三、解答題， （本大题共三、解答題， （本大题共 6 小题，共小题，共 70 分）分） 17 （12 分）在ABC 中，内角 A，B，C 所对的边分别为 a，b，c，已知 asin2BbsinA （1）求 B； （2）已知 cosA，求 sinC 的值 【分析】 （1）利用正弦定理将边化角即可得出 cosB； （2）求出 sinA，利用两角和的正弦函数公式计算 【解答】解： （1）asin2
22、BbsinA， 2sinAsinBcosBsinBsinA， cosB，B （2）cosA，sinA， sinCsin（A+B）sinAcosB+cosAsinB 【点评】本题考查了正弦定理解三角形，两角和的正弦函数，属于基础题 18 （12 分）某家电公司销售部门共有 200 位销售员，每位部门对每位销售员都有 1400 万元的年度销售任 务，已知这 200 位销售员去年完成销售额都在区间2，22（单位：百万元）内，现将其分成 5 组，第 1 组，第 2 组，第 3 组，第 4 组，第 5 组对应的区间分别为2，6） ，6，10） ，10，14） ，14，18） ，18， 22，绘制出频率分
23、布直方图 （1）求 a 的值，并计算完成年度任务的人数； （2）用分层抽样从这 200 位销售员中抽取容量为 25 的样本，求这 5 组分别应抽取的人数； （3）现从（2）中完成年度任务的销售员中随机选取 2 位，奖励海南三亚三日游，求获得此奖励的 2 位 销售员在同一组的概率 【分析】 （1）根据频率直方图即可求出 a 的值， （2）求出各组的人数比，即可求出各组的人数， （2）求出从这 6 人中随机抽取 2 人的情况总数，及两人来自同组的情况数，代入概率公式，可得答案 【解答】解： （1）2a0.25（0.02+0.08+0.09） ，解得 a0.03， 完成完成年度任务的人数 2004（
24、0.03+0.03）48 人， （2）这 5 组的人数比为 0.02：0.08：0.09：0.03：0.032：8：9：3：3， 故这 5 组分别应抽取的人数为 2，8，9，3，3 人 （3）设第四组的 4 人用 a，b，c 表示，第 5 组的 3 人用 A，B，C 表示， 从中随机抽取 2 人的所有情况如下 ab，ac，aA，aB，aC，bc，bA，bB，bC，cA，cB，cC，AB，AC， BC 共 15 种，其中在同一组的有 ab，ac，bc，AB，AC，BC 共 6 种， 故获得此奖励的 2 位销售员在同一组的概率 【点评】本题考查的知识点是频率分布直方图，古典概型，难度不大，属于基础
25、题 19（12 分） 如图， 在四棱锥 PABCD 中， ABCACD90， BACCAD60， PA平面 ABCD， PA2，AB1设 M，N 分别为 PD，AD 的中点 （1）求证：平面 CMN平面 PAB； （2）求三棱锥 PABM 的体积 【分析】 （1）推导出 MNPA，从而 MN平面 PAB，再推导出 CNAB，从而 CN平面 PAB，由此能 证明平面 CMN平面 PAB （2） 点 M 到平面 PAB 的距离等于点 C 到平面 PAB 的距离， 三棱锥 PABM 的体积 VVMPABVCPAB VPABC，由此能求出结果 【解答】证明： （1）M，N 分别为 PD，AD 的中点，
26、 MNPA 又MN平面 PAB，PA平面 PAB， MN平面 PAB 在 RtACD 中，CAD60，CNAN，ACN60 又BAC60，CNAB CN平面 PAB，AB平面 PAB，CN平面 PAB 又CNMNN，平面 CMN平面 PAB（6 分） 解： （2）由（1）知，平面 CMN平面 PAB， 点 M 到平面 PAB 的距离等于点 C 到平面 PAB 的距离 由已知，AB1，ABC90，BAC60， 三棱锥 PABM 的体积： （12 分） 【点评】本题考查面面平行的证明，考查三棱锥的体积的求法，考查推理论证能力、运算求解能力、空 间想象能力，考查化归与转化思想、数形结合思想，是中档题
27、 20 （12 分）在平面直角坐标系 xOy 中，已知椭圆 C 的中心在原点 O，焦点在 x 轴上，短轴长为 2，离心率 为，过左顶点 A 的直线 l 与椭圆交于另一点 B （）求椭圆 C 的方程； （）若|AB|，求直线 l 的倾斜角 【分析】 （）根据题目条件可列式求得椭圆方程 （）设直线 l 的方程为：yk（x+） ，代入椭圆方程，由弦长公式得到所需结论 【解答】解： （）由题意得：则得椭圆 C 的方程为 （）由题意直线得斜率存在，因为左顶点为（） 设直线 l 的方程为：yk（x+） 代入椭圆方程得： 因为一根为，则另一根为 则 AB| 化简得 8k2k70，即 k21，k1，则倾斜角为
28、 45或 135 【点评】本题主要考查了圆锥曲线方程的求法和圆锥曲线与直线的综合应用，属于中档题，在高考中时 常涉及 21 （12 分）设函数 f（x）2lnxx2+ax+2 （）当 a3 时，求 f（x）的单调区间和极值； （）若直线 yx+1 是曲线 yf（x）的切线，求 a 的值 【分析】 （）根据题意，当 a3 时，求出函数的导数，结合函数的导数与函数单调性的关系，分析函 数的单调性，进而分析可得函数的极值； （）根据题意，取出函数的导数，设直线 yx+1 与曲线 yf（x）的切点为（x0，f（x0） ） ，由导数 的几何意义求出切线的方程，分析可得答案 【解答】解：函数 f（x）2l
29、nxx2+ax+2，则 f（x）的定义域为（0，+） （）当 a3 时，f（x）2lnxx2+3x+2， 所以 令，得2x2+3x+20， 因为 x0，所以 x2f（x）与 f（x）在区间（0，+）上的变化情况如下： x （0，2） 2 （2，+） f（x） + 0 f（x） 2ln2+4 所以 f（x）的单调递增区间为（0，2） ，单调递减区间（2，+） f（x）有极大值 2ln2+4，f（x）无极小 值， （）因为 f（x）2lnxx2+ax+2， 所以 设直线 yx+1 与曲线 yf（x）的切点为（x0，f（x0） ） ， 所以，即 又因为， 即 所以 设 g（x）2lnx+x21， 因
30、为， 所以 g（x）在区间（0，+）上单调递增 所以 g（x）在区间（0，+）上有且只有唯一的零点 所以 g（1）0，即 x01 所以 a1 【点评】本题考查利用导数分析函数的单调性以及切线方程 22 （10 分）以平面直角坐标系的原点为极点，x 轴的正半轴为极轴，建立极坐标系，已知直线 l 的参数方 程是（m0，t 为参数） ，曲线 C 的极坐标方程为 2cos （）求直线 l 的普通方程和曲线 C 的直角坐标方程； （）若直线 l 与 x 轴交于点 P，与曲线 C 交于点 A，B，且|PA|PB|1，求实数 m 的值 【分析】 （）直线 L 的参数方程消去参数 t，能求出直线 l 的普通方
31、程由 2cos，得 22cos， 由此能求出曲线 C 的直角坐标方程 （）把（t 为参数） ，代入 x2+y22x，得由|PA|PB|1 |t1t2|，能求出实数 m 的值 【解答】选修 44：坐标系与参数方程来 解： （）直线 L 的参数方程是， （m0，t 为参数） ， 消去参数 t 可得 由 2cos，得 22cos， C 的直角坐标方程：x2+y22x（5 分） （）把（t 为参数） ，代入 x2+y22x， 得 由0，解得1m3， |PA|PB|1|t1t2|，m22m1， 解得或 1又满足0，m0， 实数或 m1（10 分） 【点评】本题考查直线的普通方程、曲线的直角坐标方程的求法，考查实数值的求法，考查直角坐标方 程、极坐标方程、参数方程的互化等基础知识，考查运算求解能力，考查函数与方程思想，是中档题
