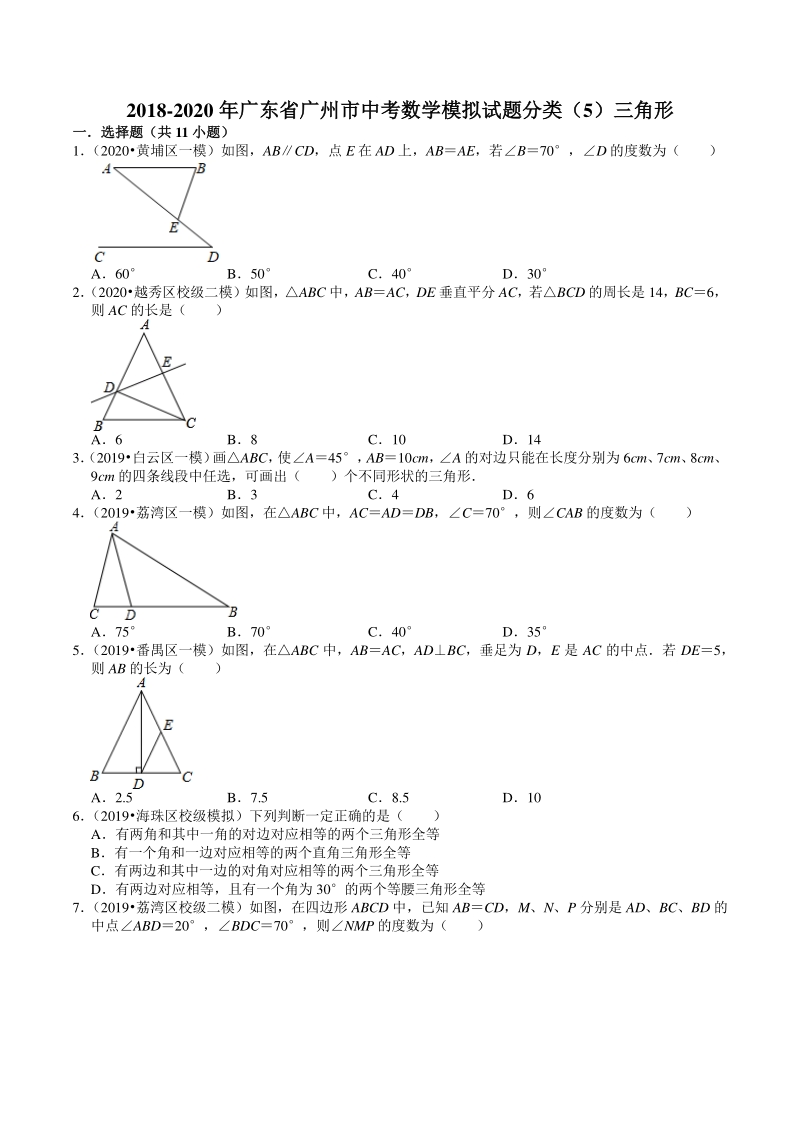
1、2018-2020 年广东省广州市中考数学模拟试题分类年广东省广州市中考数学模拟试题分类（5）三角形）三角形 一选择题（共一选择题（共 11 小题）小题） 1 （2020黄埔区一模）如图，ABCD，点 E 在 AD 上，ABAE，若B70，D 的度数为（ ） A60 B50 C40 D30 2 （2020越秀区校级二模）如图，ABC 中，ABAC，DE 垂直平分 AC，若BCD 的周长是 14，BC6， 则 AC 的长是（ ） A6 B8 C10 D14 3 （2019白云区一模） 画ABC， 使A45， AB10cm， A 的对边只能在长度分别为 6cm、 7cm、 8cm、 9cm 的四条
2、线段中任选，可画出（ ）个不同形状的三角形 A2 B3 C4 D6 4 （2019荔湾区一模）如图，在ABC 中，ACADDB，C70，则CAB 的度数为（ ） A75 B70 C40 D35 5 （2019番禺区一模）如图，在ABC 中，ABAC，ADBC，垂足为 D，E 是 AC 的中点若 DE5， 则 AB 的长为（ ） A2.5 B7.5 C8.5 D10 6 （2019海珠区校级模拟）下列判断一定正确的是（ ） A有两角和其中一角的对边对应相等的两个三角形全等 B有一个角和一边对应相等的两个直角三角形全等 C有两边和其中一边的对角对应相等的两个三角形全等 D有两边对应相等，且有一个角
3、为 30的两个等腰三角形全等 7 （2019荔湾区校级二模）如图，在四边形 ABCD 中，已知 ABCD，M、N、P 分别是 AD、BC、BD 的 中点ABD20，BDC70，则NMP 的度数为（ ） A50 B25 C15 D20 8 （2019海珠区一模）在ABC 中，D、E 分别为 AB、AC 边上中点，且 DE6，则 BC 的长度是（ ） A3 B6 C9 D12 9 （2019荔湾区校级模拟）在锐角ABC 中，三个内角的度数都是质数，则这样的三角形（ ） A只有一个且为等腰三角形 B至少有两个且都为等腰三角形 C只有一个但不是等腰三角形 D至少有两个，其中有非等腰三角形 10 （20
4、18越秀区校级一模）若等腰三角形中相等的两边的长为 10cm，第三边长为 16cm，则第三边的高为 （ ） A12cm B10cm C8cm D6cm 11 （2018荔湾区校级一模）如图，ABC 中，ABAC13，BC10，AD 平分BAC 交 BC 于点 D，点 E 为 AC 的中点，连接 DE，则CDE 的周长为（ ） A16.5 B18 C23 D26 二填空题（共二填空题（共 21 小题）小题） 12 （2020从化区一模）已知直线 l 是线段 AB 的垂直平分线，点 M，N 是直线 l 上的两点，如果NBA 15，MBA45，则MAN 13 （2020天河区一模）如图，在正方形 A
5、BCD 中，对角线 AC，BD 交于点 O，点 E，F 分别在 AB，BD 上，且ADEFDE，DE 交 AC 于点 G，连接 GF得到下列四个结论：ADG22.5；SAGD SOGD；BE2OG；四边形 AEFG 是菱形，其中正确的结论是 （填写所有正确结论的序 号） 14 （2020白云区模拟）如图，点 D 在线段 BC 上，ACBC，AB8cm，AD6cm，AC4cm，则在ABD 中，BD 边上的高是 cm 15 （2020天河区一模）如图，ABC 中，ABAC12，点 D 在 AC 上，DC4，将线段 DC 沿 CB 方向 平移 7 个单位长度得到线段 EF，此时点 E，F 分别落在边
6、 AB，BC 上，则ADE 的周长是 16 （2019黄埔区一模）在三角形 ABC 中，C90，AC8，BC6，D，E，F 分别是 AB，BC，CA 的中点，G 是重心，则 GD 17 （2019荔湾区一模）已知点 P 在线段 AB 的垂直平分线上，PA4cm，则 PB cm 18 （2019花都区一模）如图，RtABC 中，C90，AD 为的BAC 角平分线，与 BC 相交于点 D， 若 CD3，AB10，则ABD 的面积是 19 （2019荔湾区校级模拟）RtABC 内的点 P 到三边的距离均为 d，斜边为 c，则直角三角形的面积 为 20 （2019荔湾区校级二模）在边长为 4 的等边三
7、角形 ABC 中，P 是 BC 边上的一个动点，过点 P 分别作 PMAB 于 M，PNAC 于 N，连接 PA，则下列说法正确的是 （填序号） 若 PB1，则 = 13；若 PB2，则 SABC8SBMP； 四边形= 2 + 23；若 0PB1，则 S四边形AMPN最大值是33 21 （2019天河区模拟）如图，在ABC 中，ACB90，A30，AB5，点 P 是 AC 上的动点， 连接 BP， 以 BP 为边作等边BPQ， 连接 CQ， 则点 P 在运动过程中， 线段 CQ 长度的最小值是 22 （2019海珠区校级模拟）在ABC 中，边 BC 上的中线 AD 等于 9cm，那么这个三角形
8、的重心 G 到顶点 A 的距离是 cm 23 （2019海珠区校级模拟）如果一个直角三角形的两条直角边长分别为 5cm、12cm，那么这个直角三角 形斜边上的中线等于 cm 24 （2018番禺区一模）如图，在一次测绘活动中，某同学站在点 A 的位置观测停放于 B、C 两处的小船， 测得船 B 在点 A 北偏东 75方向 150 米处，船 C 在点 A 南偏东 15方向 120 米处，则船 B 与船 C 之间 的距离为 米（精确到 0.1m） 25 （2018花都区一模）如图，MON30，点 B1在 OM 边上，OB123，过点 B1作 A1B1OM 交 ON 于点 A1，以 A1B1为边在外
9、侧作等边三角形 A1B1C1，再过点 C1作 A2B2OM，分别交 OM、ON 于点 B2、 A2， 再以A2B2为边在的外侧作等边三角形A2B2C2按此规律进行下去， 则第3个等边三角形A3B3C3 的周长为 ，第 n 个等边三角形 AnBnn的周长为 （用含 n 的代数式表示） 26 （2018黄埔区一模）如图，在ABC 中，E，F 分别是 AB，AC 的中点，若中位线 EF2cm，则 BC 边 的长是 27（2018越秀区校级一模） 如图， 点A为PBC的三边垂直平分线的交点， 且P72， 则BAC 28 （2018越秀区二模） 如图， 点 D、 E 分别是ABC 的边 AC、 BC 上
10、的点， ADDE， ABBE， A80， 则BED 29 （2018海珠区一模）三角形的重心是三角形的三条 的交点 30 （2018白云区一模）如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为 16cm2，则该半圆的 半径为 cm 31 （2018白云区二模）如图，在周长为 20cm 的 ABCD 中，ABAD，AC，BD 相交于点 O，OEBD 交 AD 于 E，则ABE 的周长为 cm 32（2018越秀区校级一模） 已知ABCDEF， A52， B67， BC15cm， 则F 度， EF cm 三解答题（共三解答题（共 9 小题）小题） 33 （2020白云区二模）已知：在ABC
11、中，OB5，BAC60 （1）若 ABAC，OA3，OC4 如图 1，点 O 在ABC 内，求AOC 的度数； 如图 2，点 O 在ABC 外，求AOC 的度数； （2）如图 3，若 AB2AC，点 O 在ABC 内，且 OA= 3，AOC120，求 OC 的长 34 （2020天河区模拟）如图，ABED，EFAD，BCAD，垂足分别为 F，C，AFDC求证：BC FE 35 （2020白云区模拟）如图，在 RtABC 中，ACB90，点 O，M 分别是 RtABC 的内心和外心， 连接 OA，OB，OM （1）求AOB 的度数； （2）延长 AC 至点 D，使 ADAB，连接 BD，求证：A
12、OBD； （3）在（2）中，延长 BC 至点 E，使 BEAB，连接 DE，找出 DE 与 OM 之间的等量关系，并证明这 个结论 36 （2020越秀区一模）已知：如图，E 为 BC 上一点，ACBD，ACBE，BCBD 求证：ABDE 37 （2019南沙区一模）如图，已知在四边形 ABCD 中，点 E 在 AD 上，B+AEC180，BAC D，BCCE求证：ACDC 38 （2019番禺区一模）如图，点 C，F，E，B 在一条直线上，CFDBEA，CEBF，DFAE （1）求证：CDAB （2）判断 CDAB 是否成立，并说明理由 39 （2019越秀区校级一模）在ABC 中，BAC9
13、0，ABAC （1）如图 1，若 AB1，BD：CD1：2，求ABD 的面积 （2）如图 2，若 D 为线段 BC 上任意一点，探究 BD，CD，AD 三者之间的关系，并证明 （ 3 ） 如 图3 ， 若AB 1 ， D为 ABC内 一 点 ， 求DA+DB+DC的 最 小 值 40 （2018越秀区校级二模）如图，ABC、BEF 为等腰直角三角形，ABCBEF90，BABC， EBEF， 连接 AF、CF，M 为 AF 的中点 （1）如图 1，当 A、F、B 共线时，求证：ME= 1 2CF； （2）如图 2，当 A、F、B 不共线时，求证：ME= 1 2CF； （3）设 BC2，请直接写出
14、 BF+AF+CF 的最小值 41 （2018天河区校级一模）如图，点 E、F 在线段 BC 上，BECF，ABDC，BC78，DEC 42，求 sinA 的值 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 11 小题）小题） 1 【答案】C 【解答】解：ABAE， AEBB， B70， A40， ABCD， D40 故选：C 2 【答案】B 【解答】解：DE 垂直平分 AC， ADCD BCD 的周长是 14，BC6， ABBD+CD1468， ABAC， AC8 故选：B 3 【答案】C 【解答】解：A45，AB10cm， 点 B 到A 另一边所在直线的距离是52， AB
15、C 中，BC 52， 527， BC8 或 9， 当 BC9 时，可以构成两个三角形， 当 BC8 时，可以构成两个三角形， 一共可以画出 4 个不同的三角形； 故选：C 4 【答案】A 【解答】解：ACADDB， CADC70，BDAB， CAD180707040， ADCB+DAB， DABB35， CABCAD+DAB75， 解法二：CAB180CB180703575 故选：A 5 【答案】D 【解答】解：ADBC， ADC90， AEEC， AC2DE10， ABAC10， 故选：D 6 【答案】A 【解答】解：A、有两角和其中一角的对边对应相等的两个三角形全等，符合 AAS，正确，故
16、本选项符合 题意； B、当两三角形的直角边和斜边相等时，就不全等，故本选项不符合题意； C、有两边和其中一边的对角对应相等的两个三角形全等（SSA）不符合全等三角形的判定定理，故本选 项不符合题意； D、30角没有对应关系，不能成立，错误，故本选项不符合题意； 故选：A 7 【答案】B 【解答】解：在四边形 ABCD 中，M、N、P 分别是 AD、BC、BD 的中点， PN，PM 分别是CDB 与DAB 的中位线， PM= 1 2AB，PN= 1 2DC，PMAB，PNDC， ABCD， PMPN， PMN 是等腰三角形， PMAB，PNDC， MPDABD20，BPNBDC70， MPNMP
17、D+NPD20+（18070）130， PMN= 180130 2 =25 故选：B 8 【答案】D 【解答】解：ABC 中，D、E 分别是边 AB、AC 的中点且 DE6， BC2DE2612， 故选：D 9 【答案】A 【解答】解：90 以内的质数有： 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 质数除 2 以外均为奇数， 三个奇数相加亦为奇数， 而三角形内角和的度数为 180，是偶数， 所以必有一个角的度数为 2，不妨设A2，那么B+C17889+89， ABC 为锐角三角形，如果不取BC89，则
18、必有一角90，与锐角矛盾 所以满足条件的三角形有且仅有一个：2，89，89； 这是一个等腰三角形， 当腰为 1 时，底边远小于 1（不符合题意，舍去） ， 当底为 1 时，腰长远大于 1， 所以满足条件的互不全等的三角形有且仅有 1 个 故选：A 10 【答案】D 【解答】解：如图，过点 A 作 ADBC 于点 D， ABAC10cm， BDCD= 1 2BC= 1 2 168（cm） ， AD=2 2=6（cm） 故选：D 11 【答案】B 【解答】解：ABAC，AD 平分BAC， ADBC，DC= 1 2， BC10， DC5， 点 E 为 AC 的中点， DEEC= 1 2 =6.5，
19、CDE 的周长为：DC+EC+DE13+518， 故选：B 二填空题（共二填空题（共 21 小题）小题） 12 【答案】见试题解答内容 【解答】解：如图 1 所示，M、N 是线段 AB 的垂直平分线上的两点， NANB，MAMB， NBANAB15，MBAMAB45， MANNAB+MAB15+4560 如图 2 所示，同理可得MANMABNAB451530 故答案为：60或 30 13 【答案】见试题解答内容 【解答】解：四边形 ABCD 是正方形， GADADO45， 由ADEFDE，可得：ADG= 1 2ADO22.5， 故正确； ADEFDE， ADFD，ADGFDG， 又GDGD，
20、ADGFDG（SAS） ， SAGDSOGD， 故错误； ADEFDE， EAEF， ADGFDG， GAGF，AGDFGD， AGEFGE EFDAOF90， EFAC， FEGAGE， FGEFEG， EFGF， EFGFEAGA， 四边形 AEFG 是菱形，故正确； 四边形 AEFG 是菱形， AEFG， OGFOAB45， OGF 为等腰直角三角形， FG= 2OG， EF= 2OG， BFE 为等腰直角三角形， BE= 2EF= 2 2OG2OG， 正确 综上，正确的有 故答案为： 14 【答案】见试题解答内容 【解答】解：如图，ACBC， BD 边上的高为线段 AC 又AC4cm，
21、 BD 边上的高是 4cm 故答案是：4 15 【答案】见试题解答内容 【解答】解：ABAC， BC， CDEF，CDEF， 四边形 EFCD 是平行四边形， EDCF7，EFBC BEFB， BEEFCD4， AEAD1248， ADE 的周长为：8+8+723， 故答案为：23 16 【答案】见试题解答内容 【解答】解：在三角形 ABC 中，C90，AC8，BC6， AB=2+ 2=10， D 是 AB 的中点， CD= 1 2AB5 D，E，F 分别是 AB，BC，CA 的中点，G 是重心， GD= 1 3CD= 5 3 故答案为5 3 17 【答案】见试题解答内容 【解答】解：点 P
22、在线段 AB 的垂直平分线上， PBPA， PA4cm， PB4cm 故答案为 4cm 18 【答案】见试题解答内容 【解答】解：作 DEAB 于 E， AD 为的BAC 角平分线，C90，DEAB， DEDC3， ABD 的面积= 1 2 ABDE= 1 2 10315， 故答案为：15 19 【答案】见试题解答内容 【解答】解：设 RtABC 的两条直角边为 a，b， RtABC 内的点 P 到三边的距离均为 d，即内切圆半径为 d， + 2 = ，即 a+b2d+c， a+b+c2d+2c， 直角三角形的面积为：1 2 ( + + ) = 1 2 (2 + 2) = 2+ 故答案为：d2
23、+cd 20 【答案】见试题解答内容 【解答】解：PMAB，ABC 是等边三角形， BPM30， BM= 1 2BP= 1 2，PM= 2 2=12 (1 2) 2 = 3 2 ，AMABBM4 1 2 = 7 2， PA=2+ 2=(7 2) 2+ (3 2 )2= 13，故正确； PB2，则 P 为 BC 的中点，PA 为ABC 的高， BM= 1 2BP1，PM= 2 2=22 12= 3，PA=2 2=42 22=23， SABC= 1 2BCPA= 1 2 423 =43，SBMP= 1 2BMPM= 1 2 1 3 = 3 2 ， SABC8SBMP，故正确； 设 BPx，则 CP
24、4x， ABC 是等边三角形， BC60， PMAB，PNAC， BM= 1 2x，PM= 3 2 x，CN= 1 2（4x）2 1 2，PN= 3 2 （4x） ， AM4 1 2x，AN2+ 1 2x， 四边形 AMPN 的周长= 3 2 x+ 3 2 （4x）+4 1 2x+2+ 1 2x23 +6， 故不正确； 由得：S四边形AMPN= 1 2 （4 1 2x） 3 2 x+ 1 24 1 2（4x） 3 2 （4x）= 3 4 x2+3x+23， = 3 4 （x2）2+33， 若 0PB1，当 x1，即 PB1 时， S四边形AMPN的值= 3 4 （x2）2+33 = 113 4
25、 33，故不正确； 故答案为： 21 【答案】见试题解答内容 【解答】解：如图，取 AB 的中点 E，连接 CE，PE ACB90，A30， CBE60， BEAE， CEBEAE， BCE 是等边三角形， BCBE， PBQCBE60， QBCPBE， QBPB，CBEB， QBCPBE（SAS） ， QCPE， 当 EPAC 时，QC 的值最小， 在 RtAEP 中，AE= 5 2，A30， PE= 1 2AE= 5 4， CQ 的最小值为5 4 22 【答案】见试题解答内容 【解答】解：点 G 是ABC 的重心，D 是边 BC 的中点， 那么 AG：GD 的值为：2 1 =2， AD 等
26、于 9cm， 重心 G 到顶点 A 的距离是 6cm， 故答案为：6cm 23 【答案】见试题解答内容 【解答】解：如图，在ABC 中，C90，AC12cm，BC5cm，CD 为斜边 AB 上的中线， 则根据勾股定理知，AB=52+ 122=13cm， CD= 1 2AB= 13 2 cm； 故答案是：13 2 24 【答案】见试题解答内容 【解答】解：根据题意得：BAC90，AB150 米，AC120 米， 在 RtABC 中，BC=2+ = 3041 192.2 米， 故答案为：192.2 25 【答案】见试题解答内容 【解答】解：OB123，MON30， A1B1= 3 3 OB12，
27、B1B2= 3 2 A1B1= 3， OB2OB1+B1B233， A2B23 同理：OB3= 93 2 ，A3B3= 9 2， 三角形 A3B3C3的周长为 3A3B3= 27 2 A1B1= 3 3 OB12， A2B2 （1+ 3 2 3 3 ） A1B13， A3B3 （1+ 3 2 3 3 ） A2B2= 9 2， A4B4 （1+ 3 2 3 3 ） A3B3= 27 4 ， AnBn= (3 2) 1 3 3 OB12(3 2) 1， 第 n 个等边三角形 AnBnn的周长为 3AnBn6(3 2) 1 = 3 22 故答案为：27 2 ； 3 22 26 【答案】见试题解答内容
28、 【解答】解：ABC 中，E、F 分别是 AB、AC 的中点，EF2cm， EF 是ABC 的中位线 BC2EF224cm 故答案是：4cm 27 【答案】见试题解答内容 【解答】解：A 为PBC 三边垂直平分线的交点， 点 A 是PBC 的外心， 由圆周角定理得，BAC2BPC144， 故答案为：144 28 【答案】见试题解答内容 【解答】解：在ABD 与EBD 中， = = = ， ABDEBD， BEDA80 故答案为 80 29 【答案】见试题解答内容 【解答】解：三角形的重心是三角形的三条中线的交点 故答案为：中线 30 【答案】见试题解答内容 【解答】解：如图，圆心为 A，设大正
29、方形的边长为 2x，圆的半径为 R， 正方形有两个顶点在半圆上，另外两个顶点在圆心两侧， AEBCx，CE2x； 小正方形的面积为 16cm2， 小正方形的边长 EFDF4， 由勾股定理得，R2AE2+CE2AF2+DF2， 即 x2+4x2（x+4）2+42， 解得，x4， R45cm， 故答案为：45 31 【答案】见试题解答内容 【解答】解：AC，BD 相交于点 O O 为 BD 的中点 OEBD BEDE ABE 的周长AB+AE+BEAB+AD= 1 2 2010cm ABE 的周长为 10cm 故答案为 10 32 【答案】见试题解答内容 【解答】解：ABCDEF， EFBC15c
30、m， AD，BE， CF180AB180526761 故填 61，15 三解答题（共三解答题（共 9 小题）小题） 33 【答案】见试题解答内容 【解答】解： （1）如图 1 中，把AOC 绕点 C 逆时针旋转 60得到BCD，连接 OD ABAC，BAC60， ABC 是等边三角形， 由旋转可知，CDCO，BAOA，ACOBCD， OCDACB60， OCD 是等边三角形， ODOC4，ODC60， OB5，BDOA3， OB2BD2+OD2， ODB90， AOCBDC90+60150， 如图 2 中，将AOC 绕点 A 顺时针旋转 60得到ABD，连接 OD AOCADB， ADAO3，
31、BDCO4，OACDAB， OADBAC60， AOD 的等边三角形， ODOA3，ADO60， OB5，BD4，OD3， OB2BD2+OD2， BDC90， AOCADB906030 （2）如图 3 中，作ABQ，使得QABOAC，ABQACO，则ABQACO， AQBAOC120， AB2AC， ABQ 与ACO 的相似比为 2：1， AQ2AO23，BQ2OC，AQOQAB+BAOCAO+BAOBAC60， =2， AOQ90，OQ3， AQO30， BQOAQBAQO1203090， BQ=2 2=4， OC= 1 2BQ2 34 【答案】见试题解答内容 【解答】证明：AFDC， A
32、CDF， 又EFAD，BCAD，ABED， RtABCRtDEF（HL） ， BCFE 35 【答案】见试题解答内容 【解答】 （1）解：C90， CAB+CBA90， 点 O 是ABC 的内心， OAB+OBA= 1 2CAB+ 1 2CBA45， AOB180（OAB+OBA）135 （2）证明：如图 1 中， 点 O 是ABC 的内心， OA 平分BAD， ADAB， AOBD（等腰三角形三线合一） （3）解：结论：DE2OM 理由：如图 2 中，连接 OE，OD，延长 OM 到 K，使得 MKOM，连接 AK，BK BEBA，OBEOBA，BOBO， OBEOBA（SAS） ， OAO
33、E，BOEBOA135， AOE90，同法可证DOB90，ODOB， AMMB，OMMK， 四边形 AOBK 是平行四边形， AKOBOD，AKOB， KAO+AOB180， AOB+EOD180， KAOEOD， OAOE，AKOD， OAKEOD（SAS） ， OKED， OK2OM， DE2OM 36 【答案】见试题解答内容 【解答】证明：ACBD， ACBDBC， ACBE，BCBD， ABCEDB， ABDE 37 【答案】见试题解答内容 【解答】证明：B+AEC180 CED+AEC180 BDEC， 在ABC 和DEC 中， BDEC，BACD，BCCE， ABCDEC（AAS）
34、 ACDC； 38 【答案】见试题解答内容 【解答】证明： （1）CEBF， CEEFBFEF，即：CFBE， 在CDF 和BAE 中， = = = ， CDFBAE（SAS） ， CDBA （2）结论：CDAB 理由：由（1）知CDFBAE， CB， CDAB， 39 【答案】见试题解答内容 【解答】解： （1）BAC90，ABAC1 SABC= 1 2 11= 1 2， BD：CD1：2， SABD= 1 3 = 1 3 1 2 = 1 6； （2）探究得到的关系为：BD2+CD22AD2， 证明：作 AEBC 于 E，如图 2 所示， 由题意得：EDBEBDCDCE， 在ABC 中，BA
35、C90，ABAC， BECE= 1 2BC， 由勾股定理可得： AB2+AC2BC2， AE2AB2BE2AC2CE2，AD2AE2+ED2， 2AD22AE2+2ED2AB2BE2+（BEBD）2+AC2CE2+（CDCE）2 AB2+AC2+BD2+CD22BDBE2CDCE， AB2+AC2+BD2+CD22 1 2BCBC， BD2+CD2， 即：BD2+CD22AD2 （3）如图 3，作等边BDF 和BCE，连接 AE，交 BC 于 G， ABAC，BEEC， AE 是 BC 的垂直平分线， DBFCBE60， CBDEBF， BDBF，BCBE， CBDEBF（SAS） ， CDE
36、F， AD+BD+CDAD+DF+EFAE， 在 RtABC 中，BAC90，ABAC1， AGBGCG= 2 2 ， 在 RtBEG 中，GBE60，BG= 2 2 ， EG= 6 2 ， AE= 2+6 2 ，即 DA+DB+DC 的最小值是2+6 2 40 【答案】见试题解答内容 【解答】 （1）证明：如图 1 中，延长 FE 到 D，使 EDEF，连接 AD、BD， BEF 为等腰直角三角形，BEF90， BFE45，BEDF， BE 垂直平分 DF， BDE45， BDF 是等腰直角三角形， BDBF，DBF90， 在ABD 和CBF 中， = = = ， ABDCBF（SAS） ，
37、 ADCF， M 为 AF 的中点，DEEF， ME 是ADF 的中位线， ME= 1 2AD， ME= 1 2CF （2）证明：如图 2 中，延长 FE 到 D，使 EDEF，连接 AD、BD， BEF 为等腰直角三角形，BEF90， BFE45，BEDF， BE 垂直平分 DF， BDE45， BDF 是等腰直角三角形， BDBF，DBF90， CBF+ABFABC90， ABD+ABFDBF90， CBFABD， 在ABD 和CBF 中， = = = ， ABDCBF（SAS） ， ADCF， M 为 AF 的中点，DEEF， ME 是ADF 的中位线， ME= 1 2AD， ME= 1
38、 2CF （3）解：如图 3 中，以 CF 为边在 CF 的右侧作等边CFM，将CFB 绕点 C 逆时针旋转 60得到 CME，连接 AE，作 EHAC 于 H，在 EH 上取一点 D，使得 CDDE，连接 DC CFFM，FBME， AF+CF+FBAF+FM+ME， AEAF+FM+ME， 当 A，F，M，E 共线时，AF+FC+BF 的值最小， ACB45，BCE60， ACE45+60105， ECH75， H90， CEH15， DCDE， DCECED15， CDHDCE+DEC30 设 CHa，则 DCDE2a，DH= 3a，EH= 3a+2a， 在 RtECH 中，EC2CH2+EH2， 22a2+（3a+2a）2， a=2 3 = 62 2 （负根已经舍弃） ， 在 RtAEH 中，AH22 + 62 2 = 32+6 2 ，EH= 6+2 2 ， AE=2+ 2=(3 2+6 2 )2+ ( 6+2 2 )2= 6 + 2 41 【答案】见试题解答内容 【解答】解：C78，DEC42， D180784260， BECF， BE+EFCF+EF，即 BFCE， 在ABF 和DCE 中， = = = ， ABFDCE（SAS） ， AD60， sinAsin60= 3 2
