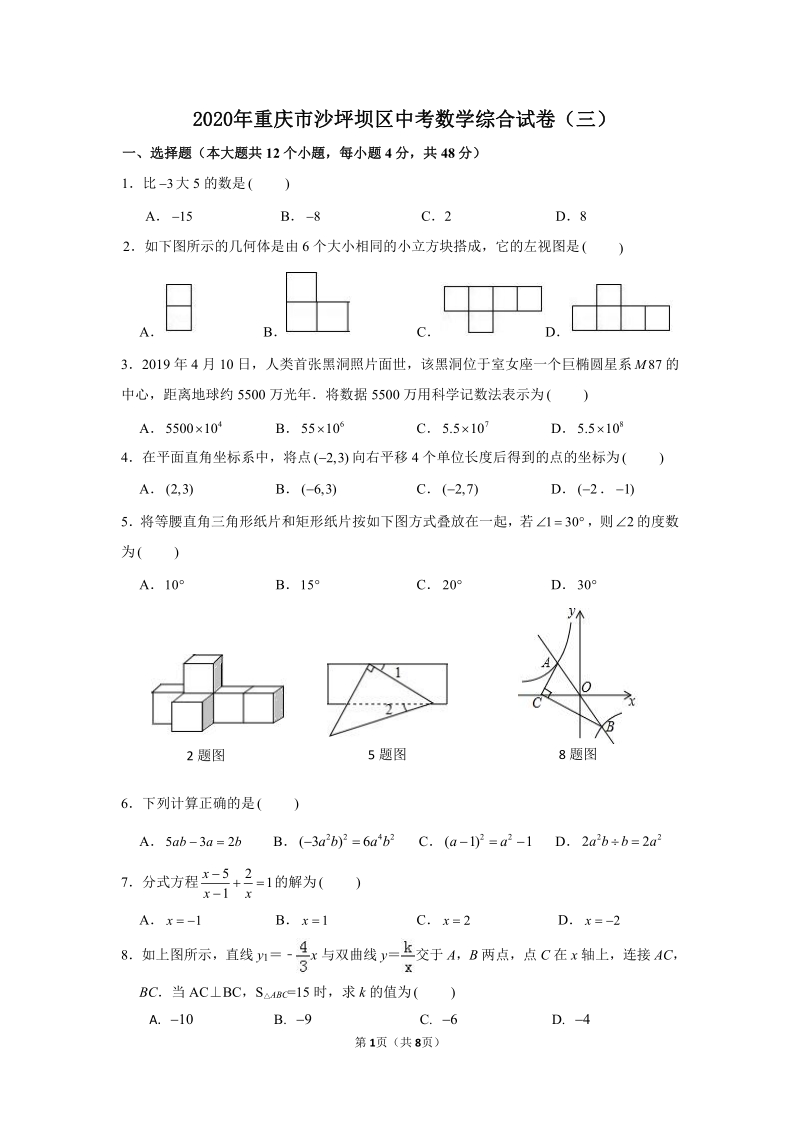
1、第 1页（共 8页） 2020年重庆市沙坪坝区中考数学综合试卷（三） 2020年重庆市沙坪坝区中考数学综合试卷（三） 一、选择题（本大题共 一、选择题（本大题共 12 个小題，每小题 个小題，每小题 4 分，共 分，共 48 分）分） 1比3大 5 的数是( ) A15 B8 C2 D8 2如下图所示的几何体是由 6 个大小相同的小立方块搭成，它的左视图是( ) ABCD 32019 年 4 月 10 日，人类首张黑洞照片面世，该黑洞位于室女座一个巨椭圆星系87M的 中心，距离地球约 5500 万光年将数据 5500 万用科学记数法表示为() A 4 5500 10B 6 55 10C 7 5
2、.5 10D 8 5.5 10 4在平面直角坐标系中，将点( 2,3)向右平移 4 个单位长度后得到的点的坐标为() A(2,3)B( 6,3)C( 2,7)D( 21) 5将等腰直角三角形纸片和矩形纸片按如下图方式叠放在一起，若130 ，则2的度数 为() A10B15C20D30 6下列计算正确的是() A532ababB 2242 ( 3)6a ba bC 22 (1)1aaD 22 22a bba 7分式方程 52 1 1 x xx 的解为() A1x B1x C2x D2x 8如上图所示，直线 y1x 与双曲线 y交于 A，B 两点，点 C 在 x 轴上，连接 AC， BC当 ACB
3、C，SABC=15 时，求 k 的值为() A.10B.9C.6D.4 2 题图5 题图8 题图 第 2页（共 8页） 9 如图， 正五边形ABCDE内接于O，P为DE上的一点 （点P不与点D重合） ， 则CPD 的度数为() A30B36C60D72 10一天，小战和同学们一起到操场测量学校旗杆高度，他们首先在斜坡底部 C 地测得旗 杆顶部 A 的仰角为 45，然后上到斜坡顶部 D 点处再测得旗杆顶部 A 点仰角为 37（身 高忽略不计） 。已知斜坡 CD 坡度1:2.4i ，坡长为 2.6 米，旗杆 AB 所在旗台高度 EF 为 1.4 米， 旗台底部、 台阶底部、 操场在同一水平面上。
4、则请问旗杆自身高度 AB 为()米。 （参考数据：sin370.6，cos370.8，tan370.75） A10.2B 9.8C 11.2D 10.8 11 若关于 x 的分式方程 1 3 22 xm xx 的解为正整数， 且关于 y 的不等式组 2()5 2 2 1+ 26 m y yy 至多有六个整数解，则符合条件的所有整数 m 的取值之和为() A1B0C5D6 12ABC 中，ACB=45，D 为 AC 上一点，AD=5 2.连接 BD，将ABD 沿 BD 翻折至 EBD， 点 A 的对应点 E 点恰好落在边 BC 上。 延长 BC 至点 F， 连接 DF， 若 CF=2， tanA
5、BD= 1 2 ， 则 DF 长为() A170B130C5 10D7 5 二、填空题（本大题共二、填空题（本大题共 6 个小题，每小题个小题，每小题 4 分，共分，共 24 分）分） 13若1m 与2互为相反数，则m的值为 14如图，在ABC中，ABAC，点D，E都在边BC上，BADCAE ，若9BD ， 则CE的长为 9 题图 10 题图 12 题图 第 3页（共 8页） 15已知一次函数(3)1ykx的图象经过第一、二、四象限，则k的取值范围是 16如图，ABCD的对角线AC与BD相交于点O，按以下步骤作图：以点A为圆心， 以任意长为半径作弧，分别交AO，AB于点M，N；以点O为圆心，以
6、AM长为半径 作弧，交OC于点 M ；以点 M 为圆心，以MN长为半径作弧，在COB内部交前面的 弧于点 N ；过点 N 作射线 ON 交BC于点E若8AB ，则线段OE的长为 17 A、B 两地之间有一修理厂 C，一日小海和王陆分别从 A、B 两地同时出发相向而行王 陆开车，小海骑摩托二人相遇时小海的摩托车突然出故障无法前行，王陆决定将小海和 摩托车一起送到修理厂 C 后再继续按原路前行，王陆到达 A 地后立即返回 B 地，到 B 地后 结束行程（装载摩托车时间和掉头时间忽略不计） ，整个行驶过程中王陆速度不变而小海 在修理厂花了十分钟修好摩托车，为了赶时间，提速 1 3 前往目的地 B，小
7、海到达 B 地后也结 束行程若图像表示的是小海与王陆二人到修理厂 C 的距离和y（km）与小海出行时间之 间x（h）的关系， 则当王陆第二次与小海在行驶中相遇时， 小海离目的地 B 还有_km. 18如图，在边长为 1 的菱形ABCD中，60ABC，将ABD沿射线BD的方向平移得 到A B D ，分别连接A C，A D，B C，则A CB C的最小值为 三、解答题（本大题共三、解答题（本大题共 4 个小题，共个小题，共 38 分分) 19（8 分）（1） 计算： 0 (2)2cos3016|13 |（2） 解不等式组： 3245, 521 1 42 xx x x 16题图 17题图 18题图
8、14题图 第 4页（共 8页） 20 （10 分）某校为了解七、八年级学生对“防溺水”安全知识的掌握情况，从七、八年级 各随机抽取 50 名学生进行测试，并对成绩（百分制）进行整理、描述和分析部分信息如 下： a七年级成绩频数分布直方图： b七年级成绩在 70 x80 这一组的是： 7072747576767777777879 c七、八年级成绩的平均数、中位数如下： 年级平均数中位数 七76.9m 八79.279.5 根据以上信息，回答下列问题： （1）在这次测试中，七年级在 80 分以上（含 80 分）的有人； （2）表中 m 的值为； （3） 在这次测试中， 七年级学生甲与八年级学 生乙的
9、成绩都是 78 分， 请判断两位学生在各自 年级的排名谁更靠前，并说明理由； （4） 该校七年级学生有 400 人， 假设全部参加 此次测试，请估计七年级成绩超过平均数 76.9 分的人数 第 5页（共 8页） 21 （10 分）如图，在平面直角坐标系xOy中，一次函数 1 5 2 yx和2yx 的图象相交于 点A，反比例函数 k y x 的图象经过点A （1）求反比例函数的表达式； （2） 设一次函数 1 5 2 yx的图象与反比例函数 k y x 的图象的另一个交点为B， 连接OB， 求ABO的面积 22 （10 分）甲、乙两人加工同一种零件，甲每天加工的数量是乙每天加工数量的 1.5 倍
10、， 两人各加工 600 个这种零件，甲比乙少用 5 天 （1）求甲、乙两人每天各加工多少个这种零件？ （2）已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元，现有 3000 个 这种零件的加工任务，甲单独加工一段时间后另有安排，剩余任务由乙单独完成如果 总加工费不超过 7800 元，那么甲至少加工了多少天？ 第 6页（共 8页） 四四、解答题（本大题共、解答题（本大题共 2 个小题，共个小题，共 20 分分) 23 （10 分）模具厂计划生产面积为 4，周长为 m 的矩形模具对于 m 的取值范围，小亮已 经能用“代数”的方法解决，现在他又尝试从“图形”的角度进行探究，过程
11、如下： （1）建立函数模型 设矩形相邻两边的长分别为 x，y，由矩形的面积为 4，得 xy4，即 y；由周长为 m， 得 2（x+y）m，即 yx+满足要求的（x，y）应是两个函数图象在第象限 内交点的坐标 （2）画出函数图象 函数y （x0） 的图象如图所示， 而函数yx+的图象可由直线yx平移得到 请 在同一直角坐标系中直接画出直线 yx （3）平移直线 yx，观察函数图象 当直线平移到与函数 y （x0） 的图象有唯一交点 （2， 2） 时， 周长 m 的值为； 在直线平移过程中，交点个数还有哪些情况？请写出交点个数及对应的周长 m 的取值 范围 （4）得出结论 若能生产出面积为 4 的
12、矩形模具，则周长 m 的取值范围为 第 7页（共 8页） 24 （10 分）如图 1 是实验室中的一种摆动装置，BC 在地面上，支架 ABC 是底边为 BC 的 等腰直角三角形，摆动臂 AD 可绕点 A 旋转，摆动臂 DM 可绕点 D 旋转，AD30，DM 10 （1）在旋转过程中， 当 A，D，M 三点在同一直线上时，求 AM 的长 当 A，D，M 三点为同一直角三角形的顶点时，求 AM 的长 （2）若摆动臂 AD 顺时针旋转 90，点 D 的位置由ABC 外的点 D1转到其内的点 D2 处，连结 D1D2，如图 2，此时AD2C135，CD260，求 BD2的长 五五、解答题（本大题共、解
13、答题（本大题共 2 个小题，共个小题，共 20 分分) 25 （10 分）如图，抛物线 2 yaxbxc经过点( 2,5)A ，与x轴相交于( 1,0)B ，(3,0)C两 点 （1）求抛物线的函数表达式； （2） 点D在抛物线的对称轴上， 且位于x轴的上方， 将BCD沿直线BD翻折得到BC D， 若点 C 恰好落在抛物线的对称轴上，求点 C 和点D的坐标； 第 8页（共 8页） 26 （10 分） 如图 1 和图 2,在ABC中,13AB ,14BC , 5 cos 13 ABC. 探究：如图 1,AHBC于点H,则AH ,AC ,ABC的面积 SABC=. 拓展：如图 2,点D在AC上(可
14、与点A,C重合),分别过点A,C作直线BD的垂线,垂足为 E,F.设BDx,AEm,CFn,(当点D与点A重合时,我们认为0 ABD S ) (1)用含x,m或n的代数式表示 ABD S及 CBD S； (2)求mn（）与x的函数关系式,并求mn（）的最大值和最小值； (3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围. 发现：请你确定一条直线,使得A,B,C三点到这条直线的距离之和最小(不必写出过程), 并写出这个最小值. 图 1 A B C H 图 2 A B C H E D F 第 1页（共 5页） 2020年重庆市沙坪坝区中考数学综合试卷（三）参考答案 一、选择题一
15、、选择题 题号123456789101112 答案CBCABDABBBAB 二、填空题二、填空题 题 号131415161718 答 案 1 93k 414 3 18.f 法一：过点 C 作直线 lBD，以直线 l 为对称轴作点 B 的对称点 E，连接 CE，AE，则 BCCE，EBD90，BE AC1.由菱形的性质可知ABDABD30， ABE3090120， 又由 ABBE1， 易求得 AE 3.在AEC 中，由三角形的三边关系可得：AC CEAE， ACCE 的最小值是3，即 ACBC 的最小 值是3. 法二：在边长为 1 的菱形ABCD中，60ABC， 1ABCD，30ABD，将ABD
16、沿射线BD的方向 平移得到A B D ，1A BAB ，/ /A BAB ，四边形 ABCD是菱形，ABCD，/ /ABCD，120BAD， A BCD ，/ /A BCD ，四边形A B CD 是平行四边形， A DB C ，A CB C的最小值A CA D的最小值， 点A在过点A且平行于BD的定直线上，作点D关于定直线的对称点E，连接CE交定直 线于A，则CE的长度即为A CB C的最小值，30A ADADB ，1AD ， 60ADE， 11 22 DHEHAD，1DE，DECD， 9030120CDEEDBCDB ，30EDCE ， 3 23 2 CECD 19.(1)解：解：原式12
17、3 2 431，(2)解： 由，得，x1， 13431，由，得，x2， 4故不等式组的解集是1x2 第 2页（共 5页） 20.解： （1）在这次测试中，七年级在 80 分以上（含 80 分）的有 15+823 人， 故答案为：23； （2）七年级 50 人成绩的中位数是第 25、26 个数据的平均数，而第 25、26 个数据分别 为 78、79， m77.5， 故答案为：77.5； （3）甲学生在该年级的排名更靠前， 七年级学生甲的成绩大于中位数 78 分，其名次在该班前 25 名， 八年级学生乙的成绩小于中位数 78 分，其名次在该班后 25 名， 甲学生在该年级的排名更靠前 （4）估计七
18、年级成绩超过平均数 76.9 分的人数为 400224（人） 21.解： （1）由 1 5 2 2 yx yx 得 2 4 x y ， ( 2,4)A， 反比例函数 k y x 的图象经过点A， 248k ， 反比例函数的表达式是 8 y x ； （2）解 8 1 5 2 y x yx 得 2 4 x y 或 8 1 x y ， ( 8,1)B， 由直线AB的解析式为 1 5 2 yx得到直线与x轴的交点为( 10,0)， 11 10410 115 22 AOB S 22.解：（1） 设乙每天加工 x 个零件， 则甲每天加工 1.5x 个零件， 由题意得：+5 化简得 6001.5600+51
19、.5x 解得 x40 1.5x60 经检验，x40 是分式方程的解且符合实际意义 第 3页（共 5页） 答：甲每天加工 60 个零件，乙每天加工，40 个零件 （2）设甲加工了 x 天，乙加工了 y 天，则由题意得 由得 y751.5x 将代入得 150 x+120（751.5x）7800 解得 x40， 当 x40 时，y15，符合问题的实际意义 答：甲至少加工了 40 天 23.户：初数 21；邮箱： bzh2解： （1）x，y 都是边长，因此，都是正数， 故点（x，y）在第一象限， 答案为：一； （2）图象如下所示： （3）把点（2，2）代入 yx+得： 22+，解得：m8； 在直线平移
20、过程中，交点个数有：0 个、1 个、2 个三种情况， 联立y和yx+并整理得： x2mx+4 0， m2440 时，两个函数有交点， 解得：m8； （4）由（3）得：m8 24.解： （1）AMAD+DM40，或 AMADDM20 显然MAD 不能为直角 当AMD 为直角时，AM2AD2DM2302102800， AM20或（20舍弃） 当ADM90时，AM2AD2+DM2302+1021000， AM10或（10舍弃） 综上所述，满足条件的 AM 的值为 20或 10 第 4页（共 5页） （2）如图 2 中，连接 CD 由题意：D1AD290，AD1AD230， AD2D145，D1D23
21、0， AD2C135， CD2D190， CD130， BACA1AD290， BACCAD2D2AD1CAD2， BAD1CAD2， ABAC，AD2AD1， BAD2CAD1（SAS） ， BD2CD130 25.解：（1） 由题意得： 425, 0 930, abc abc abc 解得 1 2 3 a b c ，抛物线的函数表达式为 2 23yxx （2）抛物线与x轴交于( 1,0)B ，(3,0)C，4BC，抛物线的对称轴为直线1x ， 如图，设抛物线的对称轴与x轴交于点H，则H点的坐 标为(1,0)，2BH ，由翻折得4C BCB， 在Rt BHC中，由勾股定理，得 2222 42
22、2 3C HC BBH， 点C的坐标为(1，2 3)， 2 3 tan3 2 C H C BH BH ， 60C BH ，由翻折得 1 30 2 DBHC BH ， 在Rt BHD中， 2 3 tan2 tan30 3 DHBHDBH ， 点D的坐标为 2 3 (1,) 3 2：26.【答案】探究： 12AH ，15AC ， 84 ABC S 拓展： （1） 1 2 ABD xmS ， 1 2 CBD xnS 第 5页（共 5页） （2） 168 mn x ；()mn的最大值为15；()mn的最小值为12 （3）x的取值范围是 56 5 x 或1314x；最小值为 56 5 【解析】探究：在直
23、角ABH中，90AHB，13AB ， 5 cos 13 ABC， cos5BHABABC，12AH ，9CHBCBH. 在ACH中，90AHC，12AH ，9CH ，15AC ， 11 14 1284 22 ABC SBC AH . 拓展： （1）由三角形的面积公式，得 11 22 ABD BD AExmS ， 11 22 CBD BD CFxnS （2）由（1）得 2 ABD S m x ， 2 BD S n x C ， 22168 ABDBD SS mn xxx C ， AC边上的高为 22 8456 15155 ABD S ， x的取值范围是 56 14 5 x. ()mn 随x的增大而减小， 当 56 5 x 时，()mn的最大值为15 当14x 时，( )mn 的最小值为12； （3）x的取值范围是 56 5 x 或1314x. 发现：ACBCAB， 过A，B，C三点到这条直线的距离之和最小的直线就是AC所在的直线，AC边上的高 的长为 56 5 .
