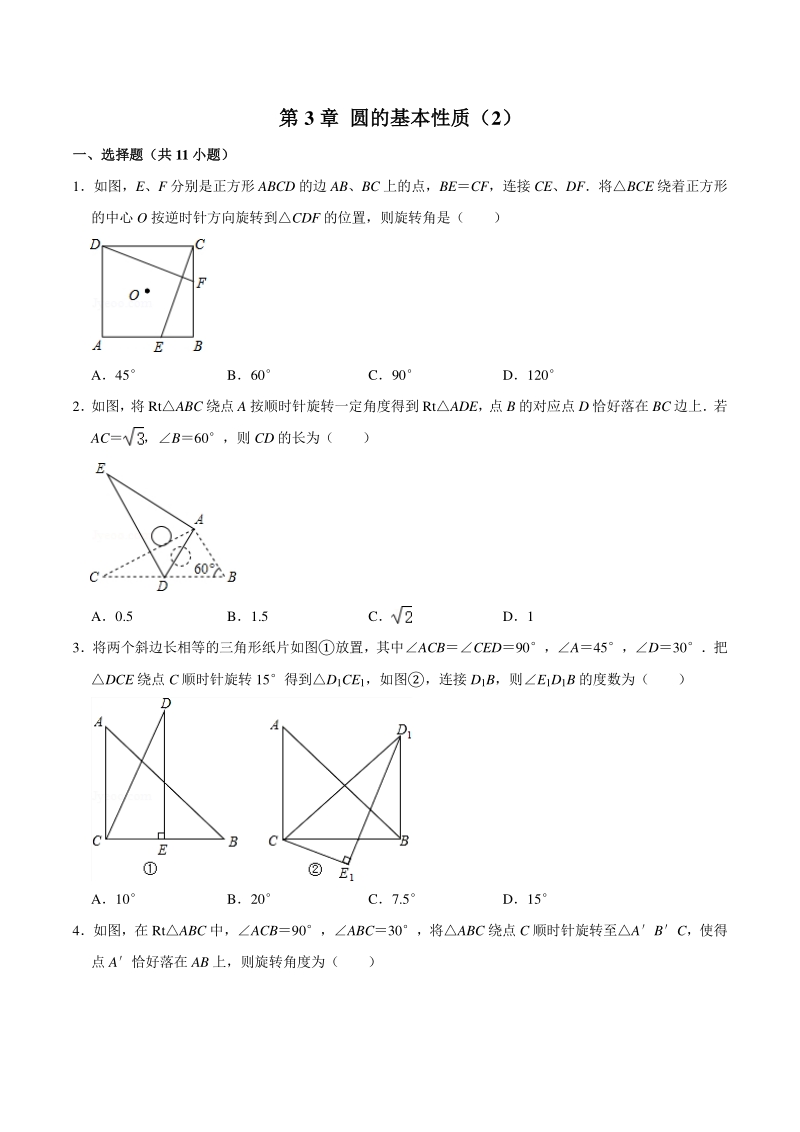
1、第第 3 章章 圆的基本性质（圆的基本性质（2） 一、选择题（共一、选择题（共 11 小题）小题） 1如图，E、F 分别是正方形 ABCD 的边 AB、BC 上的点，BECF，连接 CE、DF将BCE 绕着正方形 的中心 O 按逆时针方向旋转到CDF 的位置，则旋转角是（ ） A45 B60 C90 D120 2如图，将 RtABC 绕点 A 按顺时针旋转一定角度得到 RtADE， 点 B 的对应点 D 恰好落在 BC 边上若 AC，B60，则 CD 的长为（ ） A0.5 B1.5 C D1 3将两个斜边长相等的三角形纸片如图放置，其中ACBCED90，A45，D30把 DCE 绕点 C 顺
2、时针旋转 15得到D1CE1，如图，连接 D1B，则E1D1B 的度数为（ ） A10 B20 C7.5 D15 4如图，在 RtABC 中，ACB90，ABC30，将ABC 绕点 C 顺时针旋转至ABC，使得 点 A恰好落在 AB 上，则旋转角度为（ ） A30 B60 C90 D150 5如图，RtABC 中，ACB90，ACBC2，在以 AB 的中点 O 为坐标原点，AB 所在直线为 x 轴建 立的平面直角坐标系中，将ABC 绕点 B 顺时针旋转，使点 A 旋转至 y 轴正半轴上的 A处，则图中阴 影部分面积为（ ） A2 B C D2 6 如图， 在ABC 中， CAB70， 将ABC
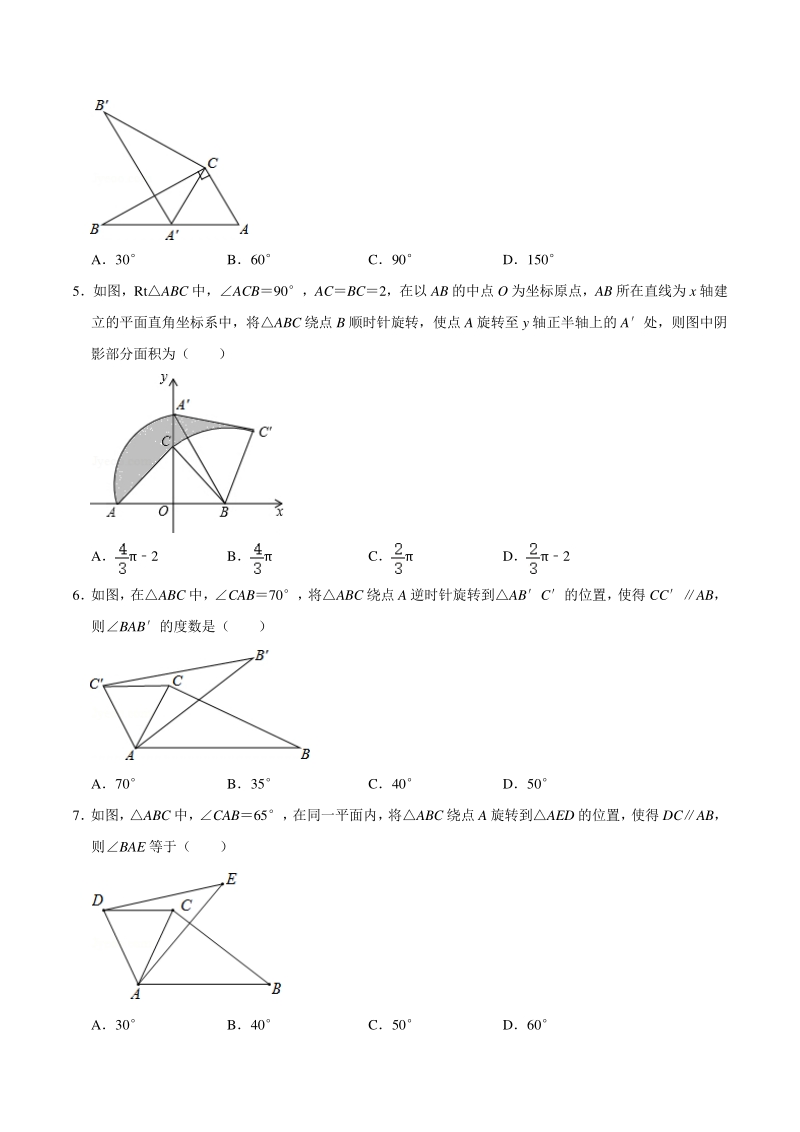
3、 绕点 A 逆时针旋转到ABC的位置， 使得 CCAB， 则BAB的度数是（ ） A70 B35 C40 D50 7 如图， ABC 中， CAB65， 在同一平面内， 将ABC 绕点 A 旋转到AED 的位置， 使得 DCAB， 则BAE 等于（ ） A30 B40 C50 D60 8如图，已知ABC 中，C90，ACBC，将ABC 绕点 A 顺时针方向旋转 60到ABC 的位置，连接 CB，则 CB 的长为（ ） A2 B C1 D1 9如图，在 RtABC 中，ACB90，B60，BC2，ABC 可以由ABC 绕点 C 顺时针旋 转得到，其中点 A与点 A 是对应点，点 B与点 B 是对
4、应点，连接 AB，且 A、B、A在同一条直 线上，则 AA的长为（ ） A6 B4 C3 D3 10如图，边长为 1 的正方形 ABCD 绕点 A 逆时针旋转 45后得到正方形 AB1C1D1，边 B1C1与 CD 交于点 O，则四边形 AB1OD 的面积是（ ） A B C D 11如图，矩形 ABCD 的外接圆 O 与水平地面相切于 A 点，圆 O 半径为 2，且2若在没有滑动的 情况下，将圆 O 向右滚动，使得 O 点向右移动了 75，则此时哪一弧与地面相切？（ ） A B C D 二、填空题（共二、填空题（共 13 小题）小题） 12如图，是将菱形 ABCD 以点 O 为中心按顺时针方
5、向分别旋转 90，180，270后形成的图形若 BAD60，AB2，则图中阴影部分的面积为 13如图，把ABC 绕点 C 按顺时针方向旋转 35，得到ABC，AB交 AC 于点 D若ADC 90，则A 14如图，ABC 绕点 A 顺时针旋转 45得到ABC，若BAC90，ABAC，则图中阴影 部分的面积等于 15如图，COD 是AOB 绕点 O 顺时针旋转 40后得到的图形，若点 C 恰好落在 AB 上，且AOD 的 度数为 90，则B 的度数是 16如图，将等边ABC 绕顶点 A 顺时针方向旋转，使边 AB 与 AC 重合得ACD，BC 的中点 E 的对应点 为 F，则EAF 的度数是 17
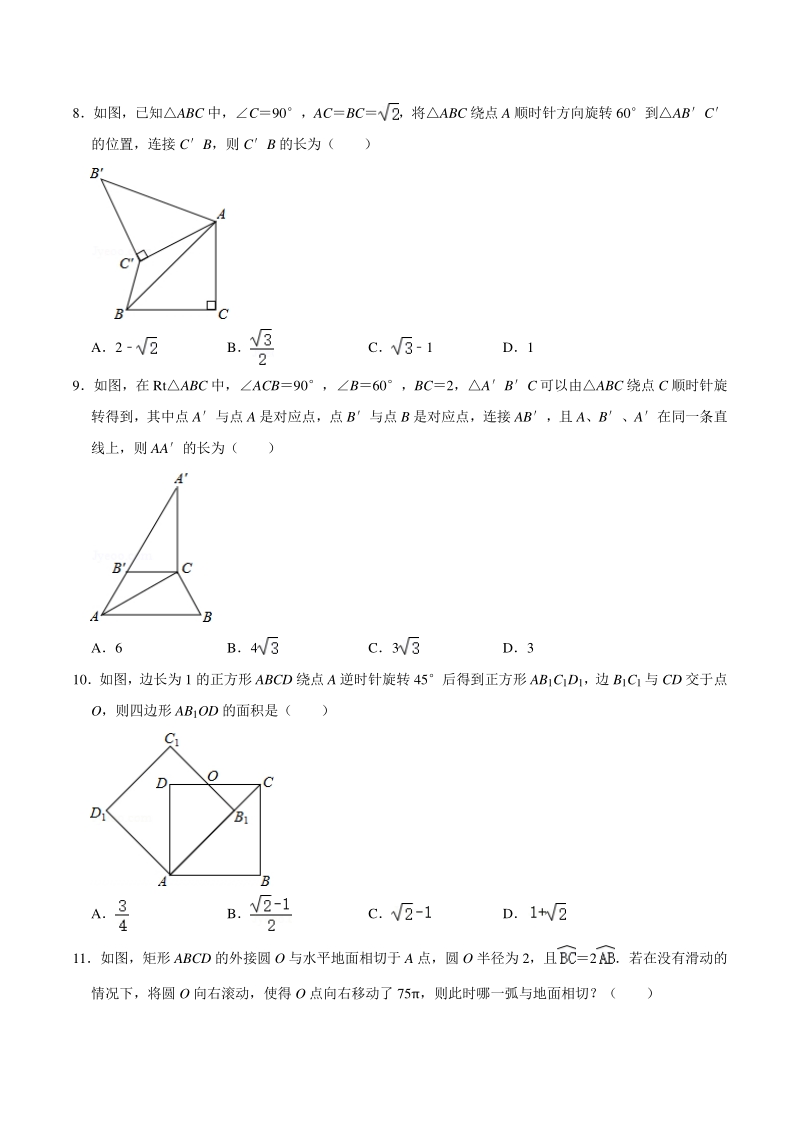
6、如图，在矩形 ABCD 中，AB，AD1，把该矩形绕点 A 顺时针旋转 度得矩形 ABCD，点 C落在 AB 的延长线上，则图中阴影部分的面积是 18如图，等腰 RtABC 中，ACB90，ACBC1，且 AC 边在直线 a 上，将ABC 绕点 A 顺时针 旋转到位置可得到点 P1，此时 AP1；将位置的三角形绕点 P1顺时针旋转到位置，可得到点 P2， 此时 AP21+； 将位置的三角形绕点 P2顺时针旋转到位置， 可得到点 P3， 此时 AP32+； ， 按此规律继续旋转，直至得到点 P2014为止则 AP2014 19如图，在正方形 ABCD 中，E、F 分别是边 BC、CD 上的点，E
7、AF45，ECF 的周长为 4，则正 方形 ABCD 的边长为 20如图（1） ，有两个全等的正三角形 ABC 和 ODE，点 O、C 分别为ABC、DEO 的重心；固定点 O， 将ODE顺时针旋转， 使得OD经过点C， 如图 （2） ， 则图 （2） 中四边形OGCF与OCH面积的比为 21如图，ABC 中，B70，BAC30，将ABC 绕点 C 顺时针旋转得EDC当点 B 的对应 点 D 恰好落在 AC 上时，CAE 22如图，两块完全相同的含 30角的直角三角板 ABC 和 ABC重合在一起，将三角板 ABC 绕其直角顶点 C按逆时针方向旋转角 （090） ，有以下四个结论： 当 30时
8、，AC 与 AB 的交点恰好为 AB 中点； 当 60时，AB恰好经过 B； 在旋转过程中，存在某一时刻，使得 AABB； 在旋转过程中，始终存在 AABB， 其中结论正确的序号是 （多填或填错得 0 分，少填酌情给分） 23如图，将OAB 绕着点 O 逆时针连续旋转两次得到OAB，每次旋转的角度都是 50若B OA120，则AOB 24如图，已知AOB90，点 A 绕点 O 顺时针旋转后的对应点 A1落在射线 OB 上，点 A 绕点 A1顺时 针旋转后的对应点 A2落在射线 OB 上，点 A 绕点 A2顺时针旋转后的对应点 A3落在射线 OB 上，连 接 AA1，AA2，AA3，依此作法，则
9、AAnAn+1等于 度 （用含 n 的代数式表示，n 为正整数） 三、解答题（共三、解答题（共 6 小题）小题） 25如图，在 RtABC 中，ACB90，B30，将ABC 绕点 C 按顺时针方向旋转 n 度后，得到 DEC，点 D 刚好落在 AB 边上 （1）求 n 的值； （2）若 F 是 DE 的中点，判断四边形 ACFD 的形状，并说明理由 26如图，已知 RtABC 中，ABC90，先把ABC 绕点 B 顺时针旋转 90至DBE 后，再把ABC 沿射线平移至FEG，DE、FG 相交于点 H （1）判断线段 DE、FG 的位置关系，并说明理由； （2）连结 CG，求证：四边形 CBEG
10、 是正方形 27 将一副三角尺 （在 RtABC 中， ACB90， B60； 在 RtDEF 中， EDF90， E45） 如图摆放，点 D 为 AB 的中点，DE 交 AC 于点 P，DF 经过点 C （1）求ADE 的度数； （2）如图，将DEF 绕点 D 顺时针方向旋转角 （060） ，此时的等腰直角三角尺记为 DEF，DE交 AC 于点 M，DF交 BC 于点 N，试判断的值是否随着 的变化而变化？如果不 变，请求出的值；反之，请说明理由 28在同一平面内，ABC 和ABD 如图放置，其中 ABBD 小明做了如下操作： 将ABC 绕着边 AC 的中点旋转 180得到CEA，将ABD
11、绕着边 AD 的中点旋转 180得到DFA， 如图，请完成下列问题： （1）试猜想四边形 ABDF 是什么特殊四边形，并说明理由； （2）连接 EF，CD，如图，求证：四边形 CDEF 是平行四边形 29已知ABC 中，M 为 BC 的中点，直线 m 绕点 A 旋转， 过 B、M、 C 分别作 BDm 于 D， MEm 于 E， CFm 于 F （1）当直线 m 经过 B 点时，如图 1，易证 EMCF （不需证明） （2）当直线 m 不经过 B 点，旋转到如图 2、图 3 的位置时，线段 BD、ME、CF 之间有怎样的数量关系？ 请直接写出你的猜想，并选择一种情况加以证明 30两个长为 2c
12、m，宽为 1cm 的长方形，摆放在直线 l 上（如图） ，CE2cm，将长方形 ABCD 绕着点 C 顺时针旋转 角，将长方形 EFGH 绕着点 E 逆时针旋转相同的角度 （1）当旋转到顶点 D、H 重合时，连接 AE、CG，求证：AEDGCD（如图） （2）当 45时（如图） ，求证：四边形 MHND 为正方形 参考答案与试题解析参考答案与试题解析 一、选择题（共一、选择题（共 11 小题）小题） 1如图，E、F 分别是正方形 ABCD 的边 AB、BC 上的点，BECF，连接 CE、DF将BCE 绕着正方形 的中心 O 按逆时针方向旋转到CDF 的位置，则旋转角是（ ） A45 B60 C
13、90 D120 【分析】首先作出旋转中心，根据多边形的性质即可求解 【解答】解：如图，连接 AC、BD，AC 与 BD 的交点即为旋转中心 O 根据旋转的性质知，点 C 与点 D 对应，则DOC 就是旋转角 四边形 ABCD 是正方形 DOC90 故选：C 【点评】本题主要考查了旋转的性质，以及正多边形的性质，正确理解正多边形的性质以及旋转角（对 应点与旋转中心所连线段的夹角等于旋转角）是解题的关键 2如图，将 RtABC 绕点 A 按顺时针旋转一定角度得到 RtADE， 点 B 的对应点 D 恰好落在 BC 边上若 AC，B60，则 CD 的长为（ ） A0.5 B1.5 C D1 【分析】
14、解直角三角形求出 AB，再求出 CB，然后根据旋转的性质可得 ABAD，然后判断出ABD 是 等边三角形，根据等边三角形的三条边都相等可得 BDAB，然后根据 CDBCBD 计算即可得解 【解答】解：B60， C906030， AC， ABACtan301， BC2AB2， 由旋转的性质得，ABAD， ABD 是等边三角形， BDAB1， CDBCBD211 故选：D 【点评】本题考查了旋转的性质，等边三角形的判定与性质，解直角三角形，熟记性质并判断出ABD 是等边三角形是解题的关键 3将两个斜边长相等的三角形纸片如图放置，其中ACBCED90，A45，D30把 DCE 绕点 C 顺时针旋转
15、15得到D1CE1，如图，连接 D1B，则E1D1B 的度数为（ ） A10 B20 C7.5 D15 【分析】根据直角三角形两锐角互余求出DCE60，旋转的性质可得BCE115，然后求出 BCD145，从而得到BCD1A，利用“边角边”证明ABC 和D1CB 全等，根据全等三角形对 应角相等可得BD1CABC45，再根据E1D1BBD1CCD1E1计算即可得解 【解答】解：CED90，D30， DCE60， DCE 绕点 C 顺时针旋转 15， BCE115， BCD1601545， BCD1A， 在ABC 和D1CB 中， ， ABCD1CB（SAS） ， BD1CABC45， E1D1B
16、BD1CCD1E1453015 故选：D 【点评】本题考查了旋转的性质，等腰直角三角形的性质，全等三角形的判定与性质，熟记性质并求出 ABC 和D1CB 全等是解题的关键 4如图，在 RtABC 中，ACB90，ABC30，将ABC 绕点 C 顺时针旋转至ABC，使得 点 A恰好落在 AB 上，则旋转角度为（ ） A30 B60 C90 D150 【分析】 根据直角三角形两锐角互余求出A60， 根据旋转的性质可得 ACAC， 然后判断出A AC 是等边三角形，根据等边三角形的性质求出ACA60，然后根据旋转角的定义解答即可 【解答】解：ACB90，ABC30， A903060， ABC 绕点
17、C 顺时针旋转至ABC 时点 A恰好落在 AB 上， ACAC， AAC 是等边三角形， ACA60， 旋转角为 60 故选：B 【点评】本题考查了旋转的性质，直角三角形两锐角互余，等边三角形的判定与性质，熟记各性质并准 确识图是解题的关键 5如图，RtABC 中，ACB90，ACBC2，在以 AB 的中点 O 为坐标原点，AB 所在直线为 x 轴建 立的平面直角坐标系中，将ABC 绕点 B 顺时针旋转，使点 A 旋转至 y 轴正半轴上的 A处，则图中阴 影部分面积为（ ） A2 B C D2 【分析】根据等腰直角三角形的性质求出 AB，再根据旋转的性质可得 ABAB，然后求出OAB 30，再
18、根据直角三角形两锐角互余求出ABA60，即旋转角为 60，再根据 S阴影S扇形ABA+S ABCSABCS扇形CBCS扇形ABAS扇形CBC，然后利用扇形的面积公式列式计算即可得解 【解答】解：ACB90，ACBC， ABC 是等腰直角三角形， AB2OA2OBAC2， ABC 绕点 B 顺时针旋转点 A 在 A处， BAAB， BA2OB， OAB30， ABA60， 即旋转角为 60， S阴影S扇形ABA+SABCSABCS扇形CBC， S扇形ABAS扇形CBC， ， ， 故选：C 【点评】本题考查了旋转的性质，等腰直角三角形的性质，直角三角形 30角所对的直角边等于斜边的 一半的性质，表
19、示出阴影部分的面积等于两个扇形的面积的差是解题的关键，难点在于求出旋转角的度 数 6 如图， 在ABC 中， CAB70， 将ABC 绕点 A 逆时针旋转到ABC的位置， 使得 CCAB， 则BAB的度数是（ ） A70 B35 C40 D50 【分析】根据旋转的性质得 ACAC，BABCAC，再根据等腰三角形的性质得ACC ACC， 然后根据平行线的性质由CCAB得ACCCAB70， 则ACCACC70， 再根据三角形内角和计算出CAC40，所以BAB40 【解答】解：ABC 绕点 A 逆时针旋转到ABC的位置， ACAC，BABCAC， ACCACC， CCAB， ACCCAB70， AC
20、CACC70， CAC18027040， BAB40， 故选：C 【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转 中心的连线段的夹角等于旋转角也考查了平行线的性质 7 如图， ABC 中， CAB65， 在同一平面内， 将ABC 绕点 A 旋转到AED 的位置， 使得 DCAB， 则BAE 等于（ ） A30 B40 C50 D60 【分析】 先根据平行线的性质得DCACAB65， 再根据旋转的性质得BAECAD， ACAD， 则根据等腰三角形的性质得ADCDCA65， 然后根据三角形内角和定理计算出CAD180 ADCDCA50，于是有BAE50
21、【解答】解：DCAB， DCACAB65， ABC 绕点 A 旋转到AED 的位置， BAECAD，ACAD， ADCDCA65， CAD180ADCDCA50， BAE50 故选：C 【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转 中心的连线段的夹角等于旋转角 8如图，已知ABC 中，C90，ACBC，将ABC 绕点 A 顺时针方向旋转 60到ABC 的位置，连接 CB，则 CB 的长为（ ） A2 B C1 D1 【分析】连接 BB，根据旋转的性质可得 ABAB，判断出ABB是等边三角形，根据等边三角形 的三条边都相等可得 ABBB，然后利用“边
22、边边”证明ABC和BBC全等，根据全等三角形 对应角相等可得ABCBBC， 延长BC交AB于D， 根据等边三角形的性质可得BDAB， 利用勾股定理列式求出 AB，然后根据等边三角形的性质和等腰直角三角形的性质求出 BD、CD，然后 根据 BCBDCD 计算即可得解 【解答】解：如图，连接 BB， ABC 绕点 A 顺时针方向旋转 60得到ABC， ABAB，BAB60， ABB是等边三角形， ABBB， 在ABC和BBC中， ， ABCBBC（SSS） ， ABCBBC， 延长 BC交 AB于 D， 则 BDAB， C90，ACBC， AB2， BD2， CD21， BCBDCD1 故选：C
23、【点评】本题考查了旋转的性质，全等三角形的判定与性质，等边三角形的判定与性质，等腰直角三角 形的性质， 作辅助线构造出全等三角形并求出 BC在等边三角形的高上是解题的关键， 也是本题的难点 9如图，在 RtABC 中，ACB90，B60，BC2，ABC 可以由ABC 绕点 C 顺时针旋 转得到，其中点 A与点 A 是对应点，点 B与点 B 是对应点，连接 AB，且 A、B、A在同一条直 线上，则 AA的长为（ ） A6 B4 C3 D3 【分析】利用直角三角形的性质得出 AB4，再利用旋转的性质以及三角形外角的性质得出 AB2， 进而得出答案 【解答】解：在 RtABC 中，ACB90，B60
24、，BC2， CAB30，故 AB4， ABC 由ABC 绕点 C 顺时针旋转得到，其中点 A与点 A 是对应点，点 B与点 B 是对应点， 连接 AB，且 A、B、A在同一条直线上， ABAB4，ACAC， CAAA30， ACBBAC30， ABBC2， AA2+46 故选：A 【点评】此题主要考查了旋转的性质以及直角三角形的性质等知识，得出 ABBC2 是解题关键 10如图，边长为 1 的正方形 ABCD 绕点 A 逆时针旋转 45后得到正方形 AB1C1D1，边 B1C1与 CD 交于点 O，则四边形 AB1OD 的面积是（ ） A B C D 【分析】连接 AC1，AO，根据四边形 A
25、B1C1D1是正方形，得出C1AB1AC1B145，求出DAB1 45，推出 A、D、C1三点共线，在 RtC1D1A 中，由勾股定理求出 AC1，进而求出 DC1OD，根据 三角形的面积计算即可 【解答】解：连接 AC1， 四边形 AB1C1D1是正方形， C1AB19045AC1B1， 边长为 1 的正方形 ABCD 绕点 A 逆时针旋转 45后得到正方形 AB1C1D1， B1AB45， DAB1904545， AC1过 D 点，即 A、D、C1三点共线， 正方形 ABCD 的边长是 1， 四边形 AB1C1D1的边长是 1， 在 RtC1D1A 中，由勾股定理得：AC1， 则 DC11
26、， AC1B145，C1DO90， C1OD45DC1O， DC1OD1， SADOODAD， 四边形 AB1OD 的面积是21， 故选：C 【点评】本题考查了正方形性质，勾股定理等知识点，主要考查学生运用性质进行计算的能力，题目比 较好，但有一定的难度 11如图，矩形 ABCD 的外接圆 O 与水平地面相切于 A 点，圆 O 半径为 2，且2若在没有滑动的 情况下，将圆 O 向右滚动，使得 O 点向右移动了 75，则此时哪一弧与地面相切？（ ） A B C D 【分析】根据题意得出圆的周长以及圆转动的周数，进而得出与地面相切的弧 【解答】解：圆 O 半径为 2， 圆的周长为：2r4， 将圆
27、O 向右滚动，使得 O 点向右移动了 75， 754183， 即圆滚动 18 周后，又向右滚动了 3， 矩形 ABCD 的外接圆 O 与水平地面相切于 A 点，2， +43， 此时与地面相切 故选：C 【点评】此题主要考查了旋转的性质以及圆的周长公式等知识，得出 O 点转动的周数是解题关键 二、填空题（共二、填空题（共 13 小题）小题） 12如图，是将菱形 ABCD 以点 O 为中心按顺时针方向分别旋转 90，180，270后形成的图形若 BAD60，AB2，则图中阴影部分的面积为 124 【分析】根据菱形的性质得出 DO 的长，进而求出 S正方形DNMF，进而得出 SADF即可得出答案 【
28、解答】解：如图所示：连接 AC，BD 交于点 E，连接 DF，FM，MN，DN， 将菱形 ABCD 以点 O 为中心按顺时针方向分别旋转 90， 180， 270后形成的图形， BAD60， AB2， ACBD，四边形 DNMF 是正方形，AOC90，BD2，AEEC， AOE45，ED1， AEEO，DO1， S正方形DNMF2（1）2（1）84， SADFADAFsin301， 则图中阴影部分的面积为：4SADF+S正方形DNMF4+84124 故答案为：124 【点评】此题主要考查了菱形的性质以及旋转的性质，得出正确分割图形得出 DO 的长是解题关键 13如图，把ABC 绕点 C 按顺时
29、针方向旋转 35，得到ABC，AB交 AC 于点 D若ADC 90，则A 55 【分析】根据题意得出ACA35，则A903555，即可得出A 的度数 【解答】解：把ABC 绕点 C 按顺时针方向旋转 35，得到ABC，AB交 AC 于点 D，A DC90， ACA35，则A903555， 则AA55 故答案为：55 【点评】此题主要考查了旋转的性质以及三角形内角和定理等知识，得出A的度数是解题关键 14如图，ABC 绕点 A 顺时针旋转 45得到ABC，若BAC90，ABAC，则图中阴影 部分的面积等于 1 【分析】根据题意结合旋转的性质以及等腰直角三角形的性质得出 ADBC1，AFFCsin
30、45 ACAC1，进而求出阴影部分的面积 【解答】解：ABC 绕点 A 顺时针旋转 45得到ABC，BAC90，ABAC， BC2，CBCACC45， ADBC，BCAB， ADBC1，AFFCsin45ACAC1， 图中阴影部分的面积等于：SAFCSDEC11（1）21 故答案为：1 【点评】此题主要考查了旋转的性质以及等腰直角三角形的性质等知识，得出 AD，AF，DC的长是解 题关键 15如图，COD 是AOB 绕点 O 顺时针旋转 40后得到的图形，若点 C 恰好落在 AB 上，且AOD 的 度数为 90，则B 的度数是 60 【分析】根据旋转的性质可得AOCBOD40，AOCO，再求出
31、BOC，ACO，然后利用三 角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解 【解答】解：COD 是AOB 绕点 O 顺时针旋转 40后得到的图形， AOCBOD40，AOCO， AOD90， BOC9040210， ACOA（180AOC）（18040）70， 由三角形的外角性质得，BACOBOC701060 故答案为：60 【点评】本题考查了旋转的性质，等腰三角形的性质，三角形的一个外角等于与它不相邻的两个内角的 和的性质，熟记各性质并准确识图是解题的关键 16如图，将等边ABC 绕顶点 A 顺时针方向旋转，使边 AB 与 AC 重合得ACD，BC 的中点 E 的对应点 为 F，
32、则EAF 的度数是 60 【分析】根据等边三角形的性质以及旋转的性质得出旋转角，进而得出EAF 的度数 【解答】解：将等边ABC 绕顶点 A 顺时针方向旋转，使边 AB 与 AC 重合得ACD，BC 的中点 E 的 对应点为 F， 旋转角为 60，E，F 是对应点， 则EAF 的度数为：60 故答案为：60 【点评】此题主要考查了等边三角形的性质以及旋转的性质，得出旋转角的度数是解题关键 17如图，在矩形 ABCD 中，AB，AD1，把该矩形绕点 A 顺时针旋转 度得矩形 ABCD，点 C落在 AB 的延长线上，则图中阴影部分的面积是 【分析】首先根据题意利用锐角三角函数关系得出旋转角的度数，
33、进而求出 SABC，S扇形BAB，即可 得出阴影部分面积 【解答】解：在矩形 ABCD 中，AB，AD1， tanCAB，ABCD，ADBC1， CAB30， BAB30， SABC1， S扇形BAB， S阴影SABCS扇形BAB 故答案为： 【点评】此题主要考查了矩形的性质以及旋转的性质以及扇形面积公式等知识，得出旋转角的度数是解 题关键 18如图，等腰 RtABC 中，ACB90，ACBC1，且 AC 边在直线 a 上，将ABC 绕点 A 顺时针 旋转到位置可得到点 P1，此时 AP1；将位置的三角形绕点 P1顺时针旋转到位置，可得到点 P2， 此时 AP21+； 将位置的三角形绕点 P2
34、顺时针旋转到位置， 可得到点 P3， 此时 AP32+； ， 按此规律继续旋转，直至得到点 P2014为止则 AP2014 1342+672 【分析】 由已知得 AP1， AP21+， AP32+； 再根据图形可得到 AP42+2； AP53+2； AP64+2；AP74+3；AP85+3；AP96+3；每三个一组，由于 20133671，则 AP2013 （2013671）+671，然后把 AP2013加上即可 【解答】解：AP1，AP21+，AP32+； AP42+2；AP53+2；AP64+2； AP74+3；AP85+3；AP96+3； 20133671， AP2013（2013671
35、）+6711342+671， AP20141342+671+1342+672 故答案为：1342+672 【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转 中心的连线段的夹角等于旋转角 19如图，在正方形 ABCD 中，E、F 分别是边 BC、CD 上的点，EAF45，ECF 的周长为 4，则正 方形 ABCD 的边长为 2 【分析】根据旋转的性质得出EAF45，进而得出FAEEAF，即可得出 EF+EC+FC FC+CE+EFFC+BC+BF4，得出正方形边长即可 【解答】解：将DAF 绕点 A 顺时针旋转 90 度到BAF位置， 由题意可得出：DA
36、FBAF， DFBF，DAFBAF， EAF45， 在FAE 和EAF中 ， FAEEAF（SAS） ， EFEF， ECF 的周长为 4， EF+EC+FCFC+CE+EFFC+BC+BFDF+FC+BC4， 2BC4， BC2 故答案为：2 【点评】 此题主要考查了旋转的性质以及全等三角形的判定与性质等知识， 得出FAEEAF是解题 关键 20如图（1） ，有两个全等的正三角形 ABC 和 ODE，点 O、C 分别为ABC、DEO 的重心；固定点 O， 将ODE 顺时针旋转，使得 OD 经过点 C，如图（2） ，则图（2）中四边形 OGCF 与OCH 面积的比为 4：3 【分析】设正三角形
37、的边长是 x，则图 1 中四边形 OGCF 是一个内角是 60的菱形，图 2 中OCH 是一 个角是 30的直角三角形，分别求得两个图形的面积，即可求解 【解答】解：设正三角形的边长是 x，则高长是x 图 1 中，四边形 OGCF 是一个内角是 60的菱形，OCxx 另一条对角线长是：FG2GH2OCtan302xtan30 x 则四边形 OGCF 的面积是：xxx2； 图 2 中，OCxx OCH 是一个角是 30的直角三角形 则OCH 的面积OCsin30OCcos30 xxx2 四边形 OGCF 与OCH 面积的比为：x2：x24：3 故答案为：4：3 【点评】本题主要考查了三角形的重心
38、的性质，解直角三角形，以及菱形、直角三角形面积的计算，正 确计算两个图形的面积是解决本题的关键 21如图，ABC 中，B70，BAC30，将ABC 绕点 C 顺时针旋转得EDC当点 B 的对应 点 D 恰好落在 AC 上时，CAE 50 【分析】利用旋转的性质得出 ACCE，以及利用三角形内角和得出BCA 的度数，利用等腰三角形的 性质得出答案 【解答】解：ABC 中，B70，则BAC30，将ABC 绕点 C 顺时针旋转得EDC，点 B 的对应点 D 恰好落在 AC 上， BCA180703080，ACCE， BCADCE80， CAEAEC（18080）50 故答案为：50 【点评】此题主要
39、考查了旋转的性质以及等腰三角形的性质，得出CAEAEC 是解题关键 22如图，两块完全相同的含 30角的直角三角板 ABC 和 ABC重合在一起，将三角板 ABC 绕其直角顶点 C按逆时针方向旋转角 （090） ，有以下四个结论： 当 30时，AC 与 AB 的交点恰好为 AB 中点； 当 60时，AB恰好经过 B； 在旋转过程中，存在某一时刻，使得 AABB； 在旋转过程中，始终存在 AABB， 其中结论正确的序号是 （多填或填错得 0 分，少填酌情给分） 【分析】 根据全等三角形的性质可得 ACAC， BCBC， 再根据旋转角求出等边三角形， 判断出 正确，求出AAC 和BBC 相似，根据
40、相似三角形对应边成比例求出 AABB，判断出错 误，再根据四边形的内角和等于 360求出 AA与 BB的夹角为 90，判断出正确 【解答】解：直角三角板 ABC 和 ABC重合在一起， ACAC，BCBC， 30时，ACB60， AC 与 AB 的交点与点 B、C 构成等边三角形， AC 与 AB 的交点为 AB 的中点，故正确； 60时，BCB60， AB恰好经过 B，故正确； 在旋转过程中，ACABCB， AACBBC， ， AABB，故错误； CAACBB（180） ， AA与 BB的夹角为 360（180）2（90+）90， 在旋转过程中，始终存在 AABB，故正确； 综上所述，结论正
41、确的是 故答案为： 【点评】本题考查了旋转的性质，等边三角形的判定与性质，等腰三角形两底角相等的性质，相似三角 形的判定与性质，熟记性质并准确识图，理清图中各角度之间的关系是解题的关键 23如图，将OAB 绕着点 O 逆时针连续旋转两次得到OAB，每次旋转的角度都是 50若B OA120，则AOB 20 【分析】根据旋转的性质得AOAAOA50，然后利用AOBBOABOB 进行 计算即可 【解答】解：AOAAOA50， BOB100， BOA120， AOBBOABOB12010020， 故答案为 20 【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等
42、 于旋转角；旋转前、后的图形全等 24如图，已知AOB90，点 A 绕点 O 顺时针旋转后的对应点 A1落在射线 OB 上，点 A 绕点 A1顺时 针旋转后的对应点 A2落在射线 OB 上，点 A 绕点 A2顺时针旋转后的对应点 A3落在射线 OB 上，连 接 AA1，AA2，AA3，依此作法，则AAnAn+1等于 （180） 度 （用含 n 的代数式表示，n 为 正整数） 【分析】 根据旋转的性质得 OAOA1， 则根据等腰三角形的性质得AA1O， 同理得到 A1AA1A2， 根据等腰三角形的性质和三角形外角性质得到AA2A1AA1O，同样得到AA3A2， 于是可推广得到AAnAn1，然后利
43、用邻补角的定义得到AAnAn+1180 【解答】解：点 A 绕点 O 顺时针旋转后的对应点 A1落在射线 OB 上， OAOA1， AA1O， 点 A 绕点 A1顺时针旋转后的对应点 A2落在射线 OB 上， A1AA1A2， AA2A1AA1O， 点 A 绕点 A2顺时针旋转后的对应点 A3落在射线 OB 上， A2AA2A3， AA3A2AA2A1， AAnAn1， AAnAn+1180 故答案为：180 【点评】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转 中心的连线段的夹角等于旋转角也考查了等腰三角形的性质 三、解答题（共三、解答题（共 6 小题）
44、小题） 25如图，在 RtABC 中，ACB90，B30，将ABC 绕点 C 按顺时针方向旋转 n 度后，得到 DEC，点 D 刚好落在 AB 边上 （1）求 n 的值； （2）若 F 是 DE 的中点，判断四边形 ACFD 的形状，并说明理由 【分析】 （1）利用旋转的性质得出 ACCD，进而得出ADC 是等边三角形，即可得出ACD 的度数； （2）利用直角三角形的性质得出 FCDF，进而得出 ADACFCDF，即可得出答案 【解答】解： （1）在 RtABC 中，ACB90，B30，将ABC 绕点 C 按顺时针方向旋转 n 度后，得到DEC， ACDC，A60， ADC 是等边三角形， A
45、CD60， n 的值是 60； （2）四边形 ACFD 是菱形； 理由：DCEACB90，F 是 DE 的中点， FCDFFE， CDFA60， DFC 是等边三角形， DFDCFC， ADC 是等边三角形， ADACDC， ADACFCDF， 四边形 ACFD 是菱形 【点评】 此题主要考查了菱形的判定以及旋转的性质和直角三角形斜边上的中线等于斜边的一半等知识， 得出DFC 是等边三角形是解题关键 26如图，已知 RtABC 中，ABC90，先把ABC 绕点 B 顺时针旋转 90至DBE 后，再把ABC 沿射线平移至FEG，DE、FG 相交于点 H （1）判断线段 DE、FG 的位置关系，并
46、说明理由； （2）连结 CG，求证：四边形 CBEG 是正方形 【分析】 （1）根据旋转和平移可得DEBACB，GFEA，再根据ABC90可得A+ACB 90，进而得到DEB+GFE90，从而得到 DE、FG 的位置关系是垂直； （2）根据旋转和平移找出对应线段和角，然后再证明是矩形，后根据邻边相等可得四边形 CBEG 是正 方形 【解答】 （1）解：FGED理由如下： ABC 绕点 B 顺时针旋转 90至DBE 后， DEBACB， 把ABC 沿射线平移至FEG， GFEA， ABC90， A+ACB90， DEB+GFE90， FHE90， FGED； （2）证明：根据旋转和平移可得GEF
47、90，CBE90，CGEB，CBBE， CGEB， BCGCBE90， 四边形 BCGE 是矩形， CBBE， 四边形 CBEG 是正方形 【点评】此题主要考查了图形的旋转和平移，关键是掌握新图形中的每一点，都是由原图形中的某一点 移动后得到的，这两个点是对应点连接各组对应点的线段平行且相等 27 将一副三角尺 （在 RtABC 中， ACB90， B60； 在 RtDEF 中， EDF90， E45） 如图摆放，点 D 为 AB 的中点，DE 交 AC 于点 P，DF 经过点 C （1）求ADE 的度数； （2）如图，将DEF 绕点 D 顺时针方向旋转角 （060） ，此时的等腰直角三角尺记
48、为 DEF，DE交 AC 于点 M，DF交 BC 于点 N，试判断的值是否随着 的变化而变化？如果不 变，请求出的值；反之，请说明理由 【分析】 （1）根据直角三角形斜边上的中线等于斜边的一半可得 CDADBDAB，根据等边对等角 求出ACDA，再求出ADC120，再根据ADEADCEDF 计算即可得解； （2）根据同角的余角相等求出PDMCDN，再根据然后求出BCD 是等边三角形，根据等边三角 形的性质求出BCD60，再根据三角形的一个外角等于与它不相邻的两个内角的和求出CPD 60， 从而得到CPDBCD， 再根据两组角对应相等， 两三角形相似判断出DPM 和DCN 相似， 再根据相似三角形对应边成比例
