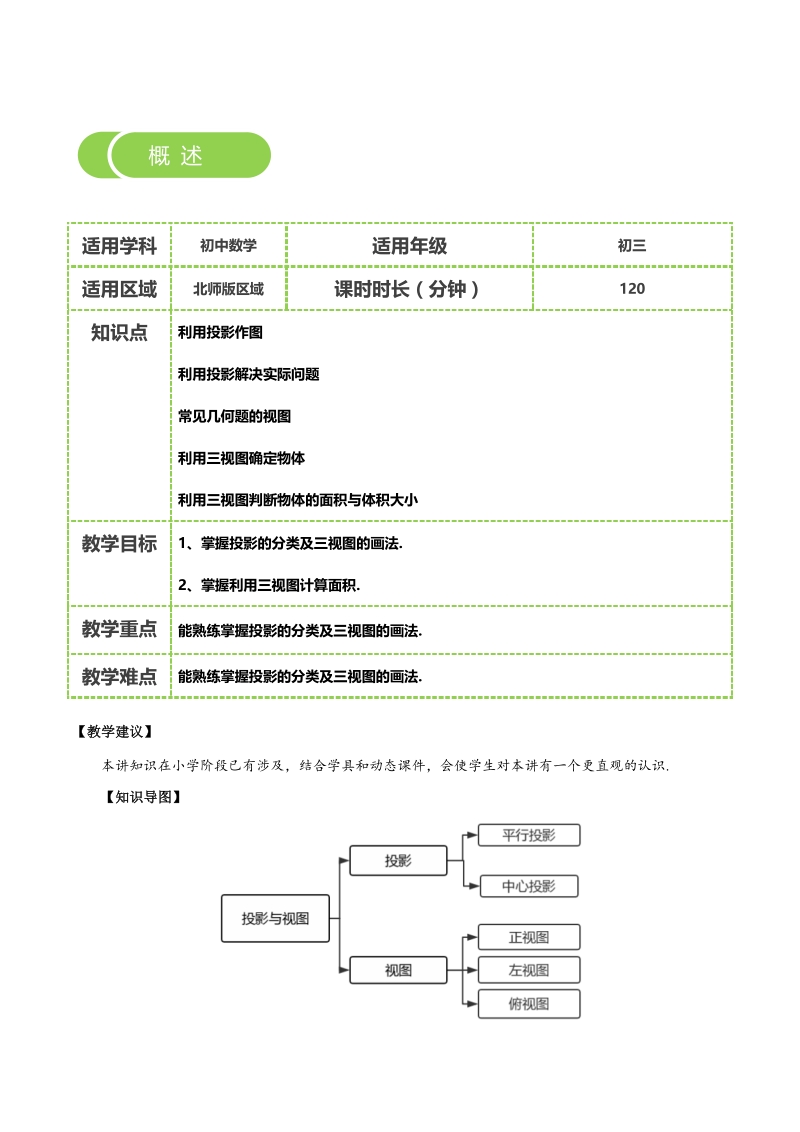
1、 投影与试图投影与试图 第14讲 适用学科 初中数学 适用年级 初三 适用区域 北师版区域 课时时长（分钟） 120 知识点 利用投影作图 利用投影解决实际问题 常见几何题的视图 利用三视图确定物体 利用三视图判断物体的面积与体积大小 教学目标 1、掌握投影的分类及三视图的画法. 2、掌握利用三视图计算面积. 教学重点 能熟练掌握投影的分类及三视图的画法. 教学难点 能熟练掌握投影的分类及三视图的画法. 【教学建议教学建议】 本讲知识在小学阶段已有涉及，结合学具和动态课件，会使学生对本讲有一个更直观的认识. 【知识导图】【知识导图】 概 述 【教学建议】【教学建议】 在这一讲知识的学习中，观察
2、能力最为重要，可以让学生结合学具来对投影和视图有一个更直观的认 识. 投影与视图也是每年中考中的热门考点，这一部分我们在小学阶段就已经接触过，本讲中我们要对投 影与试图有一个更为深入的认识. 平行投影：在平行投影中，如果三视图与投影面互相垂直，称为“正投影”，当物体面平行于投影面 时，这个面的正投影不改变这个面的形状和大小 中心投影：即点光源使物体所形成的投影. 正视图：从物体正面观察得到的图形； 左视图：从物体左面观察得到的图形； 俯视图：从物体上面观察得到的图形. 教学过程 考点 1 投影 二、知识讲解 一、导入 考点 2 视图 类型一 利用投影作图利用投影作图 已知，如图，AB 和 DE
3、 是直立在地面上的两根立柱 AB=6m，某一时刻 AB 在太阳光下的投影 BC=3m. （1）请你在图中画出此时 DE 在太阳光下的投影 EF； （2）在测量AB 的投影时，同时测量出DE 在太阳光下的投影EF 长为6m，请你计算DE 的长. 【解析】 （1） （连接 AC，过点 D 作 DF/AC，交直线 BC 于点 F，线段 EF 即为 DE 的投影） （2）AC/DF，ACB=DFE. ABC=DEF=90ABCDEF. 63 ,. 6 ABBC DEEFDE DE=12（m）. 【总结与反思】本题较为简单，利用投影作图并用相似来计算即可. 三 、例题精析 例题 1 类型二 利用投影解决
4、实际问题利用投影解决实际问题 如图，AB 和 DE 是直立在地面上的两根立柱，AB=5 米，某一时刻 AB在阳光下的投影 BC=3 米，在测量 AB 的 投影时，同时测量出 DE 在阳光下的投影长为 6 米，则 DE 的长为_ 【解析】10m 连接 AC，过点 D 作 DFAC，交直线 BE 于 F，则 EF 就是 DE 的投影 太阳光线是平行的， ACDF ACB=DFE 又ABC=DEF=90， ABCDEF EF BC DE AB ， AB=5m，BC=3m，EF=6m， 6 35 DE ， DE=10（m） 【总结与反思】 解答本题的关键是掌握平行投影的性质，根据已知得出ABCDEF
5、类型三：常见几何题的视图常见几何题的视图 例题 1 例题 1 用 4 个小立方体搭成的几何体如图请画出它的三视图. 【解析】几何体的主视图有 3 列，每列小正方形数目分别为 1，2，1；左视图有 2 列，每列小正方形数目分 别为 2，1；俯视图有 3 列，每行小正方形数目分别为 1，2，1 如图所示： 【总结与反思】 此题根据三视图的观察方法即可做出各个方向的视图. 类型四：利用三视图判断物体的面积与体积大小利用三视图判断物体的面积与体积大小 如图所示是某种型号的正六角螺母毛坯的三视图，求它的全面积. 【解析】 2 )36312(cm 侧面积=632=36（cm2）， 底面为边长为 2cm 的
6、正六边形，它可分成 6 个边长为 2cm 的 6 个等边三角形， 所以一个底面积是：6 /422=6 （cm2）， 全面积=（6 ）2+263=（12 +36）cm2. 【总结与反思】本题考查了三视图，及矩形和正六边形的面积计算，比较麻烦. 例题 1 1.如图，旗杆、树和竹竿都垂直于地面且一字排列，在路灯下树和竹竿的影子的方位和长短如图所示.请根 据图上的信息标出灯泡的位置（点 P 表示），再作出旗杆的影子（字母表示）.（不写作法，保留作图痕迹） 2.作出下面立体图形的三视图. 答案与解析答案与解析 1.【答案】见解析 【解析】 2.【答案】见解析 【解析】 四 、课堂运用 基础 1.展览厅内
7、要用相同的正方体木块搭成一个三视图如下图的展台，则此展台共需这样的正方体 块. 答案与解析答案与解析 1.【答案】10 【解析】分析：主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形 解：综合主视图，俯视图，左视图，底层有 3+1+2=6 个正方体，第二层有 2 个正方体，第三层有 2 个正方 体，所以搭成这个几何体所用的小立方块的个数是 6+2+2=10 个 1.如图是某工件的三视图，求此工件的全面积和体积 答案与解析答案与解析 1.【答案】 32 100)10100100(cmVcmS 【解析】本题考查三视图及面积，体积的计算 如图示，此工件的实物是一底面走直径为20dc
8、m，高为30hcm的圆锥. 此圆锥的底面积为 22 1 20 100 22 d S 巩固 拔高 圆锥的侧面展开图是一个扇形，此扇形的半径为 22 1 1030100010 10rcm 扇形的弧长为20ld 所以其侧面积为 2 2 10 10 10100 10SRlcm 故此圆锥的全面积为 2 12 100100 10SSScm 此圆锥的体积为 3 1 11 100301000 33 VS hcm 所以此工件的全面积为 2 100100 10cm，体积为 3 1000cm 本节的重要内容：投影与视图 投影：中心投影，平行投影 视图：正视图，左视图，俯视图 1.如图A A ，B B 是两根柱子在同
9、一灯光下的影子 （1）请在图中画出光源的位置（用点 P 表示光源）； （2）在图中画出人物 DE 在此光源下的影子（用线段 EF 表示） 2.设点 O 为投影中心，长度为 1 的线段 AB 平行于它在面 H 内的投影A B ，投影A B 的长度为 3，且 O 到直 线 AB 的距离为 1.5，那么直线 AB 与直线A B 的距离为_ 五 、课堂小结 六 、课后作业 基础 3.画出下图所示四棱柱的三视图. 4.一个几何体的三视图,那么这个几何体是 . 答案与解析答案与解析 1.【答案】 1 4 【解析】 （1）连接 A与柱子 A 的顶点，B与柱子 B 的顶点，相交于点 P，则点 P 就是光源所在
10、的位置； （2）连接 PD 并延长与底面相交于点 F，即可得到影子 EF. 解答： （1）如图所示，点 P 是影子的光源； （2）如图所示，EF 就是人在光源 P 下的影子. 2.【答案】3 【解析】ABA B ，OABOA B，对应高之比等于相似比，设 O 到A B 的距离为 h，则 1.5 AB A Bh ， 11.5 3h ，4.5h ，直线 AB 与直线A B 的距离为35 . 15 . 4，故答案为：3 3.【答案】见解析 【解析】 4.【答案】圆锥 【解析】根据三视图的知识可知该几何体为一个圆锥 解：综合主视图，俯视图，左视图可以看出这个几何体应该是圆锥 本题主要考查了根据几何体的
11、主视图、左视图、俯视图判断几何体的方法 1.四个直立在地面上的字母广告牌在丌同情况下，在地面上的投影（阴影部分）效果如图则在字母 L、K、C 的投影中，不 字母 N 属同一种投影的有 2.如图是由一些相同的小正方体构成的几何体的三视图，你知道构成这个几何体的相同的小正方体的个数 有 个. 答案与解析答案与解析 1.【答案】见解析 巩固 【解析】根据平行投影和中心投影的特点和规律“L”、“K”与“N”属中心投影； 2.【答案】5 【解析】从主视图看有 2 层 3 列，由左到右依次是第 1 列 2 层，2、3 列各 1 层；从左视图看有 2 行 2 层， 由前到后依次是第 1 行 1 层，第 2
12、行 2 层；从俯视图看有 2 行 3 列，第 1 行有 1 个小正方体，第 2 行有 3 个小正方体，综合得本题共有 5 个小正方体. 1.如图，王华晚上由路灯 A 下的 B 处走到 C 处时，测得影子 CD 的长为 1 米，继续往前走 3 米到达 E 处时， 测得影子 EF 的长为 2 米，已知王华的身高是 1.5 米. （1）求路灯 A 的高度； （2）当王华再向前走 2 米，到达 F 处时，他的影长是多少？ 2.一个长方体的三视图如图所示，若其俯视图为正方形，求这个长方体的体积. 答案与解析答案与解析 1.【答案】（1）路灯 A 有 6 米高（2）王华的影子长 8 3 米. 【解析】（1
13、）由题可知 AB/MC/NE， BD CD AB MC BF EF AB NE ，而 MC=NE BF EF BD CD CD=1 米，EF=2 米，BF=BD+4，BD=4 米，AB= 1 45 . 1 =6 米 所以路灯 A 有 6 米高 拔高 依题意，设影长为 x，则 ABBFx x身高 , 解得 3 8 x米 答：王华的影子长 8 3 米. 2.【答案】12 【解析】由图可得对角线为22，俯视图是一个正方形， 则边长为 2根据长方体体积计算公式即可解答 俯视图为正方形，则可得出边长为 2依图根据长方体体积的计算公式可知：V=223=12 考点：本题主要考查三视图的基本知识以及长方体体积计算公式 七 、教学反思
