1、 一次函数与正比例函数 第 9 讲 适用学科 初中数学 适用年级 初二 适用区域 北师版区域 课时时长（分钟） 120 知识点 函数及其表示方法 函数的值及自变量的取值范围 一次函数与正比例函数 教学目标 1、根据两个变量间的关系式，给定其中一个量，相应地会求出另一个量的值。 2、判断两个变量之间的关系是否可看作函数。 3、理解一次函数和正比例函数的概念，以及它们之间的关系。 4、能根据所给条件写出简单的一次函数表达式。 5、经历一般规律的探索过程、发展学生的抽象思维能力。 6、通过由已知信息写一次函数表达式的过程，发展学生的数学应用能力。 教学重点 1、一次函数、正比例函数的概念及关系。 2
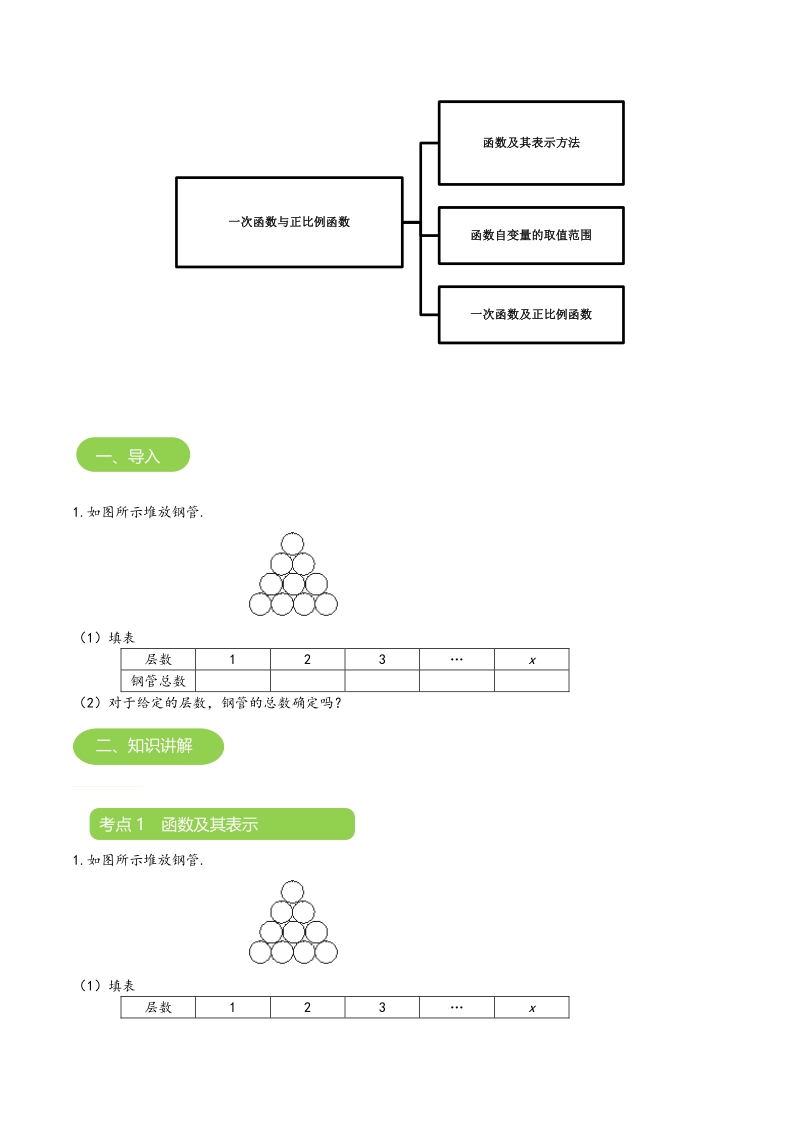
2、、会根据已知信息写出一次函数的表达式。 教学难点 会根据已知信息写出一次函数的表达式。 【教学建议教学建议】 本节课从生活实例中引入函数的概念，注意引导学生探索发现及由实例到数学模型的抽象思维能力 【知识导图】【知识导图】 概 述 1.如图所示堆放钢管. （1）填表 层数 1 2 3 x 钢管总数 （2）对于给定的层数，钢管的总数确定吗？ 1.如图所示堆放钢管. （1）填表 层数 1 2 3 x 一次函数与正比例函数一次函数与正比例函数 函数及其表示方法函数及其表示方法 函数自变量的取值范围函数自变量的取值范围 一次函数及正比例函数一次函数及正比例函数 二、知识讲解 一、导入 考点 1 函数及
3、其表示 钢管总数 （2）对于给定的层数，钢管的总数确定吗？ 2、声音在空气中传播的速度 y（m/s）（简称音速）与气温 x（）之间的关系：y= 5 3 x+331，x0， （1）当 x 分别为 5，15，30 时，你能求出相应的 y 值吗？ （2）给出任意 x，你能求出对应的 y 值吗？ 在上面各例中，都有两个变量，给定其中一个变量的值，相应地就确定了另外一个变量的值。 一般的，在一个变化过程中一般的，在一个变化过程中, ,如果有两个变量如果有两个变量 x x 与与 y y，并且对于，并且对于 x x 的每一个确定的值，的每一个确定的值，y y 都有唯一确定的值都有唯一确定的值 与其对应，那么
4、我们就说与其对应，那么我们就说 x x 是自变量，是自变量，y y 是是 x x 的函数的函数 在一个变化过程中,数值发生变化的量叫做 自变量；数值始终不变的量叫做常量 ； 函数有三种表示形式： （1）解析式法；（2）列表法；（3）图象法 函数中自变量取值范围的求法： （1）用整式表示的函数，自变量的取值范围是全体实数。 （2）用分式表示的函数，自变量的取值范围是使分母不为 0 的一切实数。 （3）用奇次根式表示的函数，自变量的取值范围是全体实数。用偶次根式表示的函数，自变量的取值范围 是使被开方数为非负数的一切实数。 （4）若解析式由上述几种形式综合而成，须先求出各部分的取值范围，然后再求其
5、公共范围，即为自变量 的取值范围。 （5）对于与实际问题有关系的，自变量的取值范围应使实际问题有意义。 有关函数问题在我们日常生活中随处可见，如弹簧秤有自然长度，在弹性限度内，随着所挂物体的重 量的增加，弹簧的长度相应的会拉长，那么所挂物体的重量与弹簧的长度之间就存在某种关系，究竟是什 么样的关系，请看： 某弹簧的自然长度为 3 厘米，在弹性限度内，所挂物体的质量 x 每增加 1 千克、弹簧长度 y 增加 0.5 厘米。 （1）计算所挂物体的质量分别为 1 千克、2 千克、3 千克、4 千克、5 千克时弹簧的长度，并填入下表： x/千克 0 1 2 3 4 5 y/厘米 3 3.5 4 4.5
6、 5 5.5 （2）你能写出 x 与 y 之间的关系式吗？ 分析：当不挂物体时，弹簧长度为 3 厘米，当挂 1 千克物体时，增加 0.5 厘米，总长度为 3.5 厘米， 当增加 1 千克物体，即所挂物体为 2 千克时，弹簧又增加 0.5 厘米，总共增加 1 厘米，由此可见，所挂物 体每增加 1 千克，弹簧就伸长 0.5 厘米，所挂物体为 x 千克，弹簧就伸长 0.5x 厘米，则弹簧总长为原长加 考点 3 一次函数及正比例函数 考点 2 函数自变量的取值范围 伸长的长度，即 y=3+0.5x。 2、做一做 某辆汽车油箱中原有汽油 100 升，汽车每行驶 50 千克耗油 9 升。 （1）完成下表：
7、 汽车行驶路程 x/千米 0 50 100 150 200 300 油箱剩余油量 y/升 你能写出 x 与 y 之间的关系吗？（y=100-0.18x 或 y=100-x 50 9 ） 3、一次函数，正比例函数的概念 上面的两个函数关系式为 y=0.5x+3， y=100-0.18x， 都是左边是因变量 y， 右边是含自变量 x 的代数式。 并且自变量和因变量的指数都是一次。若两个变量两个变量 x,yx,y 间的关系式可以表示成间的关系式可以表示成 y y= =kxkx+ +b b（k k，b b 为常数为常数 k k0 0） 的形式，则称的形式，则称 y y 是是 x x 的一次函数（的一次
8、函数（x x 为自变量，为自变量，y y 为因变量）为因变量）. .特别地，当特别地，当 b b=0=0 时，称时，称 y y 是是 x x 的正比例函数。的正比例函数。 类型一 函数及其表示 1.对于圆的面积公式S=R 2,下列说法中，正确的为（ ） A.是自变量 B.R 2是自变量 C.R 是自变量 D.R 2是自变量 【解析】C 【总结与反思】自变量与因变量. 2.下列四个图形中，不是以 x 为自变量的函数的图象是（ ） AB. C. D. 【解析】C 【总结与反思】函数的概念. 3.已知两个变量 x 和 y，它们之间的 3 组对应值如下表所示： 则 y 与 x 之间的函数关系式可能是（
9、 ） x -1 0 1 Y -1 1 3 三 、例题精析 A.yx B. 21yx C. 2 1yxx D. 3 y x 【解析】B 【总结与反思】用关系式表示函数. 类型二 函数值及自变量的取值范围 1.已知：, 3 42 x x y求：（1）求当 x 取 1，-1 时的值；（2）求当2, 3 1 , 3 1 y时 x 的值 【解析】(1) x=1 时,y=-3， x=-1 时，y= 2 1 ； （2） 3 1 y时,x= 7 9 , y= 3 1 时，x=-3， y=-2 时， 2 1 x 【总结与反思】函数求值. 2.函数 1 3 x x y中自变量的取值范围是（ ） A.3x B. 3
10、x C. 0 x且1x D. 3x，且1x 【解析】D 【总结与反思】自变量的取值范围. 类型三 一次函数及正比例函数 1.下列函数中，一次函数是（ ） A 2 8yx B. 1yx C. 8 y x D. 1 1 y x 【解析】B 【总结与反思】一次函数概念. 2.下列函数中，是正比例函数的是（） A.y = -8x B . x y 8 C. y=5 +6 D.y=-0.5x-1 【解析】A 【总结与反思】正比例函数概念. 1.为迎接省运会在某市召开，市里组织了一个梯形鲜花队参加开幕式，要求共站 60 排，第一排站 40 人， 四 、课堂运用 基础 后面每一排都比前一排多站一人，则每排的人
11、数 y 与该排的排数 x 之间的函数关系式 . 2.已知函数 3 1 x y x ，当10 x 时，y 的值为（ ） A. 7 9 B. 9 7 C. 7 3 D. 3 7 3.下列问题中，变量之间的关系是正比例函数关系的是（） A.长方形的面积固定，长和宽之间的关系 B.正方形的面积和边长之间的关系 C.三角形的面积一定，底边和底边上的高之间的关系 D.匀速运动中，路程和时间之间的关系 4.下列函数：yx； 4 x y ； 4 y x ；21yx；2yx； 1 3 2 x y ； 2 32yx. 其中是一次函数的个数是（ ） A.3 B.4 C.5 D.6 答案与解析答案与解析 1.【答案】
12、39yx，160 x 【解析】用关系式表示函数. 2.【答案】C 【解析】求函数值. 3.【答案】D 【解析】用函数关系式表示变量之间的关系及正比例函数. 4.【答案】C 【解析】一次函数概念. 1.下列变量之间的关系： （1）多边形的对角线条数与边数； （2）三角形面积与它的底边长； （3）x-y=3 中的 x 与 y； （4）32 xy中的 y 与 x； （5）圆面积与圆的半径。 其中成函数关系的有（ ） 巩固 A.2 个 B.3 个 C.4 个 D.5 个 2.若 y= 2 2 1 m xm ）（是正比例函数，则 m 的值为（） B.-1 C.1 或-1 D. 或- 3.下列函数：ykx
13、， 2 3 yx， 2 1yxxx， 2 1yx， 2 2yx，一定是一次函 数的有（ ） A.3 个 B.2 个 C.4 个 D.5 个 4.下列函数中，是一次函数但不是正比例函数的是（ ） A. 3 x y B. 3 y x C. 1 2 x y D. 2 21 2 x y x 答案与解析答案与解析 1.【答案】C 【解析】本题主要考查函数的概念. 2.【答案】B 【解析】本题主要考查正比例函数的概念. 3.【答案】A 【解析】本题主要考查一次函数的概念 4.【答案】C 【解析】本题主要考查一次函数与正比例函数的区别. 1.下列各曲线中，反映了变量 y 是 x 的函数的是（ ） A. B.
14、 C. D. 2.函数 0 2 3 x yx x 中，自变量 x 的取值范围是 . 拔高 3.下列说法中正确的是（ ） A一次函数是正比例函数 B.正比例函数不是一次函数 C. 不是正比例函数就不是一次函数 D.不是一次函数就不是正比例函数 4.若 y=（m-2）x+(m-2)是正比例函数，则 m 的值为（） A. 2 B.-2 C. 2 D.任意实数 答案与解析答案与解析 1.【答案】C 【解析】本题主要考查函数的概念. 2.【答案】 0 x 且 3x 【解析】本题主要考查函数自变量的取值范围. 3.【答案】D 【解析】本题主要考查一次函数与正比例函数的区别与联系. 4.【答案】B 【解析】
15、本题主要考查正比例函数的概念. 本节讲了 3 个重要内容： 1.函数及其表示方法 2.函数的值及自变量的取值范围 3.一次函数与正比例函数 五 、课堂小结 六 、课后作业 1.甲、乙两地相距 S 千米，某人行完全程所用的时间 t（时）与他的速度 v（千米/时）满足 vt=S，在这个 变化过程中，下列判断中错误的是（ ）. A.S 是变量 B.t 是变量 C.v 是变量 D.S 是常量 2.假设甲、乙两人在一次赛跑中，路程 S 与时间 t 的关系如图，那么可知道： （1）这是一次 米赛跑； （2）甲、乙两人中先到达终点是 . 3.如果函数 | | 1 24 n ynx 是一次函数，则此函数的关系
16、式为（ ） A4yx B.44yx C.44yx D.44yx 答案与解析答案与解析 1.【答案】A 【解析】函数中变量与常量的判定. 2.【答案】（1）100 米； （2）甲 【解析】由图像表示函数关系. 3.【答案】D 【解析】本题主要考查一次函数的概念. 1.等腰三角形顶角的度数 y（单位：度）与底角的度数 x（单位：度）之间的函数关系式及 x 的取值范围是 （ ） A1802090yxx B. 180090yxx C1802090yxx D. 180090yxx 2.如果函数(2)3yax是一次函数，那么a的取值范围是_. 3.已知3y 与x成正比例，且当2x 时，7y . 巩固 基础
17、 （1）写出y与x之间的函数关系式；（2）当4x 时，求y的值；（3）当4y 时，求x的值； 4.容积为 800L 的水池内已贮水 200L，若每分钟注入的水量是 15L，设池内的水量为 Q（L），注水时间为 t （min）. （1）请写出 Q 与 t 的函数关系式.（2）注水多长时间可以把水池注满？（3）当注水时间为 0.2h 时，池中 水量是多少？ 答案与解析答案与解析 1.【答案】C 【解析】用关系式表示函数及自变量的取值范围. 2.【答案】 2a 【解析】本题主要考查一次函数的概念. 3.【答案】(1)23yx ；(2)11；(3) 1 2 【解析】本题主要考查正比例关系式及函数求值.
18、 4.【答案】 2a 【解析】（1）Q=200+15t，0t40.（2）注水 40min 可以把水池注满.（3）380L 1.已知函数31 2ya xa . （1）当a取何值时，这个函数是一次函数？（2）当a取何值时，这个函数是正比例函数？ 2.如图,在三角形 ABC 中,B 与C 的平分线交于点 P, 设A=x,BPC=y,当A 变化时,求y与x之间的函数关 系式,并判断y是不是x的一次函数. 拔高 P A BC 3.我国现行个人工资薪金所得税征收办法规定：月收入低于 2000 元的部分不收税；月收入超过 2000 元但 低于 2500 元的部分征收 5%的所得税如某人月收入 2300 元，
19、他应缴个人工资薪金所得税为（2300-2000） 5%=15（元） （1）当月收入大于 2000 元而又小于 2500 元时，写出应缴所得税 y（元）与月收入 x（元）之间的关系式； （2）某人月收入为 2100 元，他应缴所得税多少元？ （3）如果某人本月缴所得税 1.92 元，那么此人本月工资薪金是多少元？ 答案与解析答案与解析 1.【答案】（1）a3 时；（2） 1 2 【解析】本题主要考查一次函数及正比例函数的概念. 2.【答案】 1 90 2 yx，(0 180 )x ； y 是x的一次函数. 【解析】用关系式表示函数的应用. 3.【答案】解：（1）月收入大于 2000 元而又小于 2500 元， 应缴所得税 y（元）与月收入 x（元）之间的关系式为； y=（x-2000）5% =0.05x-100； （2）根据题意得： （2100-2000）5%=5（元）， 答：他应缴所得税 5 元 （3）此人本月工资薪金是 x 元，根据题意得： （x-2000）5%=1.92， 解得：x=2038.4， 则此人本月工资薪金是 2038.4 元 【解析】用关系式表示函数的应用. 七 、教学反思
