1、2020 年江苏年江苏南京南京中考数学一模二模试题分类（中考数学一模二模试题分类（6）概率与统计概率与统计 一选择题（共一选择题（共 7 小题）小题） 1 （2020秦淮区二模）数据 76，78，80，82，84 的方差是（ ） A2.4 B4 C4.8 D8 2 （2020秦淮区一模）在某市 2019 年青少年航空航天模型锦标赛中，各年龄组的参赛人数情况如表所示： 年龄组 13 岁 14 岁 15 岁 16 岁 参赛人数 5 19 12 14 若小明所在年龄组的参赛人数占全体参赛人数的 38%，则小明所在的年龄组是（ ） A13 岁 B14 岁 C15 岁 D16 岁 3 （2020南京二模
2、）已知一组数据 5，6，7，8，9，5，9，若增加一个数 7，则新的这组数据与原来相比 （ ） A平均数变大，方差变大 B平均数不变，方差变大 C平均数不变，方差变小 D平均数不变，方差不变 4 （2020建邺区一模）小敏参加了某次演讲比赛，根据比赛时七位评委所给的分数制作了如下表格： 平均数/分 中位数/分 众数/分 方差/分 2 8.8 8.9 8.5 0.14 如果去掉一个最高分和一个最低分，那么表格中数据一定不发生变化的是（ ） A平均数 B中位数 C众数 D方差 5 （2020鼓楼区一模）某班 37 名同学中只有 1 位同学身高是 165cm若除甲、乙外其余 35 名同学身高的 平均
3、数和中位数都是 165cm， 则该班 37 名同学身高的平均数 a 和中位数 b （单位： cm） ， 不可能是 （ ） Aa165，b165 Ba165，b165 Ca165，b164 Da165，b166 6 （2020鼓楼区校级模拟）有 15 位同学参加数学竞赛，已知他们的得分互不相同，取 8 位同学进入决赛， 小明同学知道了自己的分数后，想知道自己能否进入决赛，还需知道这 15 位同学分数的（ ） A平均数 B众数 C中位数 D方差 7 （2020鼓楼区校级二模）为了比较甲乙两足球队的身高谁更整齐，分别量出每人身高，发现两队的平均 身高一样，甲、乙两队的方差分别是 1.7、2.4，则下
4、列说法正确的是（ ） A甲、乙两队身高一样整齐 B甲队身高更整齐 C乙队身高更整齐 D无法确定甲、乙两队身高谁更整齐 二填空题（共二填空题（共 3 小题）小题） 8 （2020秦淮区二模）某校初中女子篮球队共有 11 名队员，她们的年龄情况如下： 年龄/岁 12 13 14 15 人数 1 3 3 4 则该篮球队队员年龄的中位数是 岁 9 （2020浦口区二模）某商场统计了去年 15 月 A，B 两种品牌冰箱的销售情况 A 品牌（台） 15 17 16 13 14 B 品牌（台） 10 14 15 16 20 则这段时间内这两种品牌冰箱月销售量较稳定的是 （填“A”或“B” ） 10 （202
5、0鼓楼区一模）一组数据 2，3，2，3，5 的方差是 三解答题（共三解答题（共 24 小题）小题） 11 （2020秦淮区二模） “科技兴国” 科技企业在社会生产生活中的地位越来越重要调查某科技企业五 年以来的研发成本和年度利润率，将相关数据绘制成统计图和统计表： 2015 年2019 年利润率： 年份 利润率 2015 年 6.3% 2016 年 5.2% 2017 年 6.7% 2018 年 9.1% 2019 年 17.4% （1）2019 年度该企业总成本是 亿元； （2）求该企业五年以来的年平均研发成本； （3）根据统计图和统计表中的信息，进行综合分析，写出两个不同类型的结论 12
6、（2020秦淮区二模）在一个不透明的袋子中有 1 个红球，2 个白球和若干个黑球小明将袋子中的球摇 匀后，从中任意摸出一个球，记下颜色后放回袋中并摇匀，在多次重复以上操作后，小明统计了摸到红 球的频率，并绘制了如折线统计图： （1）袋子中一共有 个球； （2）若从该袋中同时摸出 2 个球，求摸出的 2 个球都是白球的概率 13 （2020玄武区二模）某校为了解七、八年级学生英语听力训练情况（七八年级学生人数相同） ，某周从 这两个年级学生中分别随机抽查了 50 名同学，调查了他们周一至周五的听力训练情况，根据调查情况得 到如下统计图： （1）根据上述统计图完成下表中的相关统计量： 年级 平均训
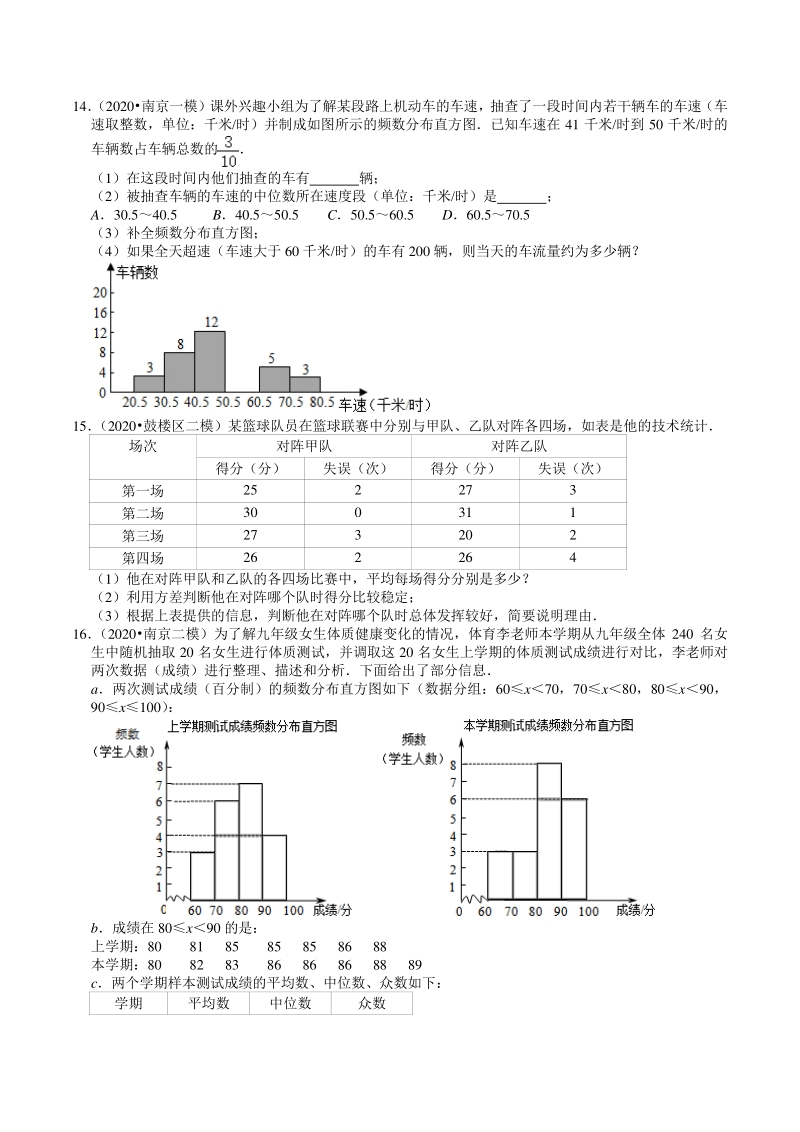
7、练时间的中位数 平时训练时间的方差 七年级 20.8 八年级 27 （2）请你利用上述统计图，对七八年级英语听力训练情况写出两条合理的评价 14 （2020南京一模）课外兴趣小组为了解某段路上机动车的车速，抽查了一段时间内若干辆车的车速（车 速取整数，单位：千米/时）并制成如图所示的频数分布直方图已知车速在 41 千米/时到 50 千米/时的 车辆数占车辆总数的 （1）在这段时间内他们抽查的车有 辆； （2）被抽查车辆的车速的中位数所在速度段（单位：千米/时）是 ； A30.540.5 B40.550.5 C50.560.5 D60.570.5 （3）补全频数分布直方图； （4）如果全天超速（
8、车速大于 60 千米/时）的车有 200 辆，则当天的车流量约为多少辆？ 15 （2020鼓楼区二模）某篮球队员在篮球联赛中分别与甲队、乙队对阵各四场，如表是他的技术统计 场次 对阵甲队 对阵乙队 得分（分） 失误（次） 得分（分） 失误（次） 第一场 25 2 27 3 第二场 30 0 31 1 第三场 27 3 20 2 第四场 26 2 26 4 （1）他在对阵甲队和乙队的各四场比赛中，平均每场得分分别是多少？ （2）利用方差判断他在对阵哪个队时得分比较稳定； （3）根据上表提供的信息，判断他在对阵哪个队时总体发挥较好，简要说明理由 16 （2020南京二模）为了解九年级女生体质健康变
9、化的情况，体育李老师本学期从九年级全体 240 名女 生中随机抽取 20 名女生进行体质测试，并调取这 20 名女生上学期的体质测试成绩进行对比，李老师对 两次数据（成绩）进行整理、描述和分析下面给出了部分信息 a两次测试成绩（百分制）的频数分布直方图如下（数据分组：60 x70，70 x80，80 x90， 90 x100） ： b成绩在 80 x90 的是： 上学期：80 81 85 85 85 86 88 本学期：80 82 83 86 86 86 88 89 c两个学期样本测试成绩的平均数、中位数、众数如下： 学期 平均数 中位数 众数 上学期 84 a 85 本学期 b c d 根据
10、以上信息，回答下列问题： （1）表中 a 的值是 ； （2）下列关于本学期样本测试成绩的结论：c86；d86；成绩的极差可能为 41；b 有可能等 于 80其中所有正确结论的序号是 ； （3）从两个不同角度分析这 20 名女生从上学期到本学期体质健康变化情况 17 （2020鼓楼区二模）甲盒中有标号为 1，2，3 的牌子，乙盒中有标号为 1，2，3，4 的牌子，两个盒子 均不透明，这些牌子除标号外无其他差别小勇从甲盒中随机摸出一个牌子，标号为 a，小婷从乙盒中 随机摸出一个牌子，标号为 b，若 ab，则小勇获胜；若 ab，则小婷获胜 （1）求小勇获胜的概率； （ 2 ） 若 小 勇 摸 出 的
11、 牌 子 标 号 为2 ， 在 不 知 道 小 婷 标 号 的 情 况 下 ， 他 获 胜 的 概 率 是 18 （2020南京二模）经过某路口的汽车，可能直行，也可能向左转或向右转如果这三种可能性大小相 同，现有甲、乙、丙三辆汽车经过这个路口 （1）求甲、乙两辆汽车向同一方向行驶的概率； （2）甲、乙、丙三辆汽车向同一方向行驶的概率是 19 （2020建邺区一模）某校七、八、九年级共有 1000 名学生学校统计了各年级学生的人数，绘制了图 、图两幅不完整的统计图 （1）将图的条形统计图补充完整 （2）图中，表示七年级学生人数的扇形的圆心角度数为 （3）学校数学兴趣小组调查了各年级男生的人数，
12、绘制了如图所示的各年级男生人数占比的折线统计 图（年级男生人数占比100%） 请结合相关信息，绘制一幅适当的统计图，表示 各年级男生及女生的人数，并在图中标明相应的数据 20 （2020玄武区一模） 某班有甲、 乙两名同学报名参加 100 米跑步比赛， 他们在赛前进行了 10 次训练 将 两人的 10 次训练成绩分别绘制成如图统计图 （1）根据统计图把下列表格补充完整： 平均数（s） 方差（s2） 跑进 15s 以内（不包括 15s）的占比 甲 15 50% 乙 15 0.038 （2）从两个不同角度评价甲、乙两名同学的训练成绩 21 （2020秦淮区一模）面对今年的新冠疫情，某区所有中学开展
13、了“停课不停学”活动该区教育主管 部门随机调查了一些家长对该活动的态度（A：无所谓；B：赞成；C：反对） ，并将调査结果绘制成图 和图的统计图请根据图中提供的信息，解答下列问题： （1）在图中，C 部分所占扇形的圆心角度数为 ； （2）将图补充完整； （ 3 ） 根 据 抽 样 调 查 结 果 ， 估 计 该 区 30000 名 中 学 生 家 长 中 有 多 少 人 持 赞 成 态 度 ？ 22 （2020浦口区模拟）一个不透明的布袋中仅有 2 个红球、1 个黑球，这些球除颜色外无其他差别 （1）甲同学先随机摸出一个小球，记下颜色后放回搅匀，再随机摸出一个小球，则两次摸出的小球颜色 不同的概
14、率是多少？ （2）乙同学从中一次摸出两个球，则摸出的小球均为红色的概率是 23 （2020建邺区一模）疫情期间的某一天， “建邺云课堂”为学生提供了语文、数学、英语三个学科各一 节微课，甲、乙两名同学随机选择一节微课自主学习 （1）甲同学选择数学微课的概率是 ； （2）求甲、乙两名同学选择同一学科微课的概率 24 （2020玄武区一模）某校对高一新生随机摇号分班，一共分 4 个班，班号分别为 1 班、2 班、3 班、4 班，甲、乙两人是该校的高一新生 （1）甲恰好被分在 1 班的概率为 ； （2）求甲、乙被分在班号连续的两个班级的概率 25 （2020鼓楼区一模） （1）不透明的袋子 A 中装
15、有红球 1 个、白球 1 个，不透明的袋子 B 中装有红球 1 个、白球 2 个，这些球除颜色外无其他差别分别从两个袋子中随机摸出一个球，求摸出的两个球颜色 不同的概率； （2）甲、乙两人解同一道数学题，甲正确的概率为，乙正确的概率为，则甲乙恰有一人正确的概率 是 26 （2020秦淮区一模）到目前为止，北京是世界上唯一一个既举办过夏季奥运会，又即将举办冬季奥运 会的城市以下四个是北京奥运会、残奥会、冬奥会及冬残奥会的会徽 （1）从中任意抽取一个会徽，恰好是“中国印舞动的北京”的概率为 ； （2）从中任意抽取两个会徽，求恰好是“冬梦”和“飞跃”的概率 27 （2020鼓楼区一模）如图是某区 1
16、500 名小学生和初中生的视力情况和他们每节课课间户外活动平均时 长的统计图 （1）根据图 1，计算该区 1500 名学生的近视率； （2）根据图 2，从两个不同的角度描述该区 1500 名学生各年级近视率的变化趋势； （3）根据图 1、图 2、图 3，描述该区 1500 名学生近视率和所在学段（小学、初中） 、每节课课间户外 活动平均时长的关系 28 （2020玄武区模拟）如图，A、B、C 三个完全一样的不透明杯子依次排成一排，倒扣在水平桌面上， 其中一个杯子里有一枚硬币 （1）随机翻开一个杯子，出现硬币的概率是 ； （2）同时随机翻开两个杯子，求出现硬币的概率； （3）若这枚硬币在 A 杯
17、内，现从三个杯子中随机选择两个交换位置（硬币随 A 杯一起移动） ，则经过两 次交换后，硬币恰好在中间位置的杯子内的概率为 A.B.C.D. 29 （2020玄武区模拟）为了支持新冠肺炎疫情防控工作，某社区积极响应党的号召，鼓励共产党员踊跃 捐款为了了解该社区共产党员的捐款情况，抽取了部分党员的捐款金额进行统计，数据整理成如图尚 不完整的统计表和统计图 某社区抽样党员捐款金额统计表 组别 捐款金额（元） 人数 A x100 2 B 100 x200 10 C 200 x300 D 300 x400 14 E x400 4 （1）一共抽取了 名党员，捐款金额的中位数在 中（填组别） ； （2）补
18、全条形统计图，并算出扇形统计图中 B 组对应扇形的圆心角度数为 ； （3）该社区共有 1000 名党员，请估计捐款金额超过 300 元的党员有多少名？ 30 （2020浦口区模拟）丁老师为了解所任教的两个班的学生数学学习情况，对数学进行了一次测试，获 得了两个班的成绩（百分制） ，并对数据（成绩）进行整理、描述和分析，下面给出了部分信息 A、B 两班学生（两个班的人数相同）数学成绩不完整的频数分布直方图如下（数据分成 5 组：x60， 60 x70，70 x80，80 x90，90 x100） ： A、B 两班学生测试成绩在 80 x90 这一组的数据如下： A 班：80 80 82 83 8
19、5 85 86 87 87 87 88 89 89 B 班：80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89 A、B 两班学生测试成绩的平均数、中位数、方差如下： 平均数 中位数 方差 A 班 80.6 m 96.9 B 班 80.8 n 153.3 根据以上信息，回答下列问题： （1）补全数学成绩频数分布直方图； （2）写出表中 m、n 的值； （3）请你对比分析 A、B 两班学生的数学学习情况（至少从两个不同的角度分析） 31 （2020南京二模）一个不透明箱子中有 2 个红球，1 个黑球和 1 个白球，四个
20、小球的形状、大小完全相 同 （1）从中随机摸取 1 个球，则摸到黑球的概率为 （2）小明和小贝做摸球游戏，游戏规则如下 游戏规则 让小明先从箱子中随机摸取 个小球，记下颜色后放回箱子， 摇匀后再让小贝随机摸取一个小 球，记下颜色，若两人所摸小球的 颜色相同，则小明胜：反之，则小 贝胜 你认为这个游戏公平吗？请说明理由 32 （2020玄武区二模）校园歌手大赛中甲乙丙 3 名学生进入了决赛，组委会决定通过抽签确定表演顺序 （1）求甲第一个出场的概率； （2）求甲比乙先出场的概率 33 （2020浦口区二模）网瘾低龄化问题已经引起社会各界的高度关注，有关部门在全国范围内对 1235 岁的网瘾人群进
21、行了简单的随机抽样调查，绘制出如图两幅统计图 请根据图中的信息，回答下列问题： （1）这次抽样调查中共调查了 人，并请补全条形统计图； （2）扇形统计图中 1823 岁部分的圆心角的度数是 度； （3）据报道，目前我国 1235 岁网瘾人数约为 2000 万，请估计其中 1223 岁的人数 34 （2020浦口区二模）初三（1）班要从、乙、丙、丁这 4 名同学中随机选取 2 名同学参加学校毕业生代 表座谈会，求下列事件的概率 （1）已确定甲参加，另外 1 人恰好选中乙； （2）随机选取 2 名同学，恰好选中甲和乙 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 7 小题）小题）
22、 1 （2020秦淮区二模）数据 76，78，80，82，84 的方差是（ ） A2.4 B4 C4.8 D8 【答案】D 【解答】解：平均数为： （76+78+80+82+84）580， 方差为：S2（7680）2+（7880）2+（8080）2+（8280）2+（8480）2 8 故选：D 2 （2020秦淮区一模）在某市 2019 年青少年航空航天模型锦标赛中，各年龄组的参赛人数情况如表所示： 年龄组 13 岁 14 岁 15 岁 16 岁 参赛人数 5 19 12 14 若小明所在年龄组的参赛人数占全体参赛人数的 38%，则小明所在的年龄组是（ ） A13 岁 B14 岁 C15 岁
23、D16 岁 【答案】B 【解答】解：根据各年龄组的参赛人数情况表可知： 总参赛人数为：5+19+12+1450， 195038%， 则小明所在的年龄组是 14 岁 故选：B 3 （2020南京二模）已知一组数据 5，6，7，8，9，5，9，若增加一个数 7，则新的这组数据与原来相比 （ ） A平均数变大，方差变大 B平均数不变，方差变大 C平均数不变，方差变小 D平均数不变，方差不变 【答案】C 【解答】解：数据 5，6，7，8，9，5，9 的平均数为： 7， s2（57）2+（67）2+（77）2+（87）2+（97）2+（57）2+（97）272， 若增加一个数 7， 则新的数据与原来相比
24、平均数不变， 新的数据的方差：s2（57）2+（67）2+（77）22+（87）2+（97）2+（57）2+（97） 28 ， 则方差变小 故选：C 4 （2020建邺区一模）小敏参加了某次演讲比赛，根据比赛时七位评委所给的分数制作了如下表格： 平均数/分 中位数/分 众数/分 方差/分 2 8.8 8.9 8.5 0.14 如果去掉一个最高分和一个最低分，那么表格中数据一定不发生变化的是（ ） A平均数 B中位数 C众数 D方差 【答案】B 【解答】解：如果去掉一个最高分和一个最低分，则平均数、众数可能发生变化，数据的波动性变小， 方差变小， 而 7 个数据按由小到大排列， 最中间的一个数没
25、有变化， 所以数据的中位数一定不发生变化 故选：B 5 （2020鼓楼区一模）某班 37 名同学中只有 1 位同学身高是 165cm若除甲、乙外其余 35 名同学身高的 平均数和中位数都是 165cm， 则该班 37 名同学身高的平均数 a 和中位数 b （单位： cm） ， 不可能是 （ ） Aa165，b165 Ba165，b165 Ca165，b164 Da165，b166 【答案】D 【解答】解：因为 35 名同学身高的平均数和中位数都是 165cm，且只有 1 位同学身高是 165cm，如果甲 乙两同学身高都大于 165，中位数可能是 166，但平均数大于 165；如果甲乙两同学身高
26、都小于 165，中 位数小于 165， 平均数小于 165； 如果甲乙两同学身高一个大于 165， 一个小于 165， 则平均数可能是 165， 但中位数只能是 165， 故选：D 6 （2020鼓楼区校级模拟）有 15 位同学参加数学竞赛，已知他们的得分互不相同，取 8 位同学进入决赛， 小明同学知道了自己的分数后，想知道自己能否进入决赛，还需知道这 15 位同学分数的（ ） A平均数 B众数 C中位数 D方差 【答案】C 【解答】解：由于 15 个人中，第 8 名的成绩是中位数，故小明同学知道了自己的分数后，想知道自己能 否进入决赛，还需知道这 15 位同学的分数的中位数 故选：C 7 （
27、2020鼓楼区校级二模）为了比较甲乙两足球队的身高谁更整齐，分别量出每人身高，发现两队的平均 身高一样，甲、乙两队的方差分别是 1.7、2.4，则下列说法正确的是（ ） A甲、乙两队身高一样整齐 B甲队身高更整齐 C乙队身高更整齐 D无法确定甲、乙两队身高谁更整齐 【答案】B 【解答】解：甲、乙两队的方差分别是 1.7、2.4， S甲 2S 乙 2， 甲队身高更整齐； 故选：B 二填空题（共二填空题（共 3 小题）小题） 8 （2020秦淮区二模）某校初中女子篮球队共有 11 名队员，她们的年龄情况如下： 年龄/岁 12 13 14 15 人数 1 3 3 4 则该篮球队队员年龄的中位数是 1
28、4 岁 【答案】14 【解答】解：一共有 11 个数据，其中位数为第 6 个数据， 这组数据的中位数为 14 岁， 故答案为：14 9 （2020浦口区二模）某商场统计了去年 15 月 A，B 两种品牌冰箱的销售情况 A 品牌（台） 15 17 16 13 14 B 品牌（台） 10 14 15 16 20 则这段时间内这两种品牌冰箱月销售量较稳定的是 A （填“A”或“B” ） 【答案】见试题解答内容 【解答】解：A 品牌的销售量的平均数为15， B 品牌的销售量的平均数为15， A 品牌的方差（1315）2+（1415）2+（1515）2+（1615）2+（1715）22， B 品牌的方差
29、（1015）2+（1415）2+（1515）2+（1615）2+（2015）210.4， 因为 10.42，所以 A 品牌的销售量较为稳定 A， 故答案为 A 10 （2020鼓楼区一模）一组数据 2，3，2，3，5 的方差是 1.2 【答案】见试题解答内容 【解答】解： （2+3+3+3+5）53， S2（23）2+（33）2+（33）2+（23）2+（53）21.2 故填答案为 1.2 三解答题（共三解答题（共 24 小题）小题） 11 （2020秦淮区二模） “科技兴国” 科技企业在社会生产生活中的地位越来越重要调查某科技企业五 年以来的研发成本和年度利润率，将相关数据绘制成统计图和统计
30、表： 2015 年2019 年利润率： 年份 利润率 2015 年 6.3% 2016 年 5.2% 2017 年 6.7% 2018 年 9.1% 2019 年 17.4% （1）2019 年度该企业总成本是 17 亿元； （2）求该企业五年以来的年平均研发成本； （3）根据统计图和统计表中的信息，进行综合分析，写出两个不同类型的结论 【答案】见试题解答内容 【解答】解： （1）2019 年度该企业总成本是 5.1（170%）17（亿元） ， 故答案为：17 （2） （0.5+1.2+2+3.5+5.1）52.46（亿元） 该企业五年以来的年平均研发成本为 2.46 亿元 （3） 该企业 2
31、019 年的总成本为 17 亿元， 2019 年的利润率是 17.4%， 所以 2019 年的利润是 1717.4% 2.958（亿元） 该企业近五年的研发成本分别是 0.5 亿元、 1.2 亿元、 2 亿元、 3.5 亿元、 5.1 亿元， 年利润率分别是 6.3%、 5.2%、6.7%、9.1%、17.4%，可以看出增加研发成本短期会使得年利润率下降，但是长期能使得年利润 率大幅上升 说明：两个结论，但应注意“综合分析” 静态写实型，直接陈述图中信息的，得 0 分，例如： “2019 年的研发成本为 5.1 亿元” 只写出一个结论，对某一组数据进行分析，例如： “5 年来研发成本逐年上升”
32、 ，或者两组数据建立联 系的，例如参考答案中的或 两个不同类型结论中，两个都是对某一组数据进行分析，例如： “5 年来研发成本逐年上升”和“5 年 来利润率第一年下降然后逐年上升” 两个不同类型结论中，有一个类型是对某一组数据进行分析，例如： “5 年来利润率第一年下降然后逐 年上升” ，另一类型是两组数据建立联系的，例如参考答案中的或 12 （2020秦淮区二模）在一个不透明的袋子中有 1 个红球，2 个白球和若干个黑球小明将袋子中的球摇 匀后，从中任意摸出一个球，记下颜色后放回袋中并摇匀，在多次重复以上操作后，小明统计了摸到红 球的频率，并绘制了如折线统计图： （1）袋子中一共有 5 个球
33、； （2）若从该袋中同时摸出 2 个球，求摸出的 2 个球都是白球的概率 【答案】见试题解答内容 【解答】解： （1）观察折线统计图可知： 摸到红球的频率稳定在 0.2， 设袋子中有 x 个黑球， 所以0.2， 解得 x2， 所以袋子中一共有 5 个球 故答案为：5； （2）解：将 2 个白球分别记作“白 1” 、 “白 2” ， 2 个黑球分别记作“黑 1” 、 “黑 2” 从袋中同时摸出 2 个球， 可能出现的结果有 10 种， 即（红，白 1） ， （红，白 2） ， （红，黑 1） ， （红，黑 2） ， （白 1，白 2） ， （白 1，黑 1） ， （白 1，黑 2） ， （白 2
34、，黑 1） ， （白 2，黑 2） ， （黑 1，黑 2） ， 并且它们出现的可能性相同 其中 2 个球都是白球（记为事件 A）的结果有 1 种，即（白 1，白 2） ， 所以 P（A） 13 （2020玄武区二模）某校为了解七、八年级学生英语听力训练情况（七八年级学生人数相同） ，某周从 这两个年级学生中分别随机抽查了 50 名同学，调查了他们周一至周五的听力训练情况，根据调查情况得 到如下统计图： （1）根据上述统计图完成下表中的相关统计量： 年级 平均训练时间的中位数 平时训练时间的方差 七年级 24 20.8 八年级 27 7.6 （2）请你利用上述统计图，对七八年级英语听力训练情况写
35、出两条合理的评价 【答案】见试题解答内容 【解答】解： （1）七年级平均训练时间的中位数是 24 分钟； 八年级平时训练时间的平均数是：（23+25+27+30+30）27（分钟） ， 则八年级平时训练时间的方差是：（2327）2+（2527）2+（2727）2+2（3027）27.6； 故答案为：24，7.6； （2）八年级的平均训练时间的中位数比七年级的平均训练时间中位数大； 八年级平时训练时间的方差小于七年级平时训练时间的方差，说明八年级的平均训练时间更加稳定 14 （2020南京一模）课外兴趣小组为了解某段路上机动车的车速，抽查了一段时间内若干辆车的车速（车 速取整数，单位：千米/时）
36、并制成如图所示的频数分布直方图已知车速在 41 千米/时到 50 千米/时的 车辆数占车辆总数的 （1）在这段时间内他们抽查的车有 40 辆； （2）被抽查车辆的车速的中位数所在速度段（单位：千米/时）是 B ； A30.540.5 B40.550.5 C50.560.5 D60.570.5 （3）补全频数分布直方图； （4）如果全天超速（车速大于 60 千米/时）的车有 200 辆，则当天的车流量约为多少辆？ 【答案】见试题解答内容 【解答】解： （1）观察统计图知：车速在 41 千米/时到 50 千米/时的车辆数为 12，占总数的， 则在这段时间内他们抽查的车有：1240（辆） ； 故答案
37、为：40； （2）共 40 辆车，处于中间位置的是第 20、21 辆车的速度的平均数， 被抽查车辆的车速的中位数所在速度段（单位：千米/时）是 40.550.5； 故答案为：B； （3）50.560.5 的车辆数是：403812539（辆） ，补全统计图如下： （4）2001000（辆） ， 答：当天的车流量约为 1000 辆 15 （2020鼓楼区二模）某篮球队员在篮球联赛中分别与甲队、乙队对阵各四场，如表是他的技术统计 场次 对阵甲队 对阵乙队 得分（分） 失误（次） 得分（分） 失误（次） 第一场 25 2 27 3 第二场 30 0 31 1 第三场 27 3 20 2 第四场 26
38、2 26 4 （1）他在对阵甲队和乙队的各四场比赛中，平均每场得分分别是多少？ （2）利用方差判断他在对阵哪个队时得分比较稳定； （3）根据上表提供的信息，判断他在对阵哪个队时总体发挥较好，简要说明理由 【答案】见试题解答内容 【解答】解： （1）甲队的平均每场得分是27（分） ； 乙队的平均每场得分是26（分） ； （2）甲队的方差是：（2527）2+（3027）2+（2727）2+（2627）23.5； 乙队的方差是：（2726）2+（3126）2+（2026）2+（2626）215.5； 3.515.5， 他在对阵甲队时得分比较稳定； （3）他在对阵甲队时总体发挥较好，理由：甲队的平均数
39、大于乙队的平均数，而甲队的方差小于乙队的 方差， 他对阵甲队平均失误是1.75 次，对阵乙队的平均失误为2.5 次， 所以他在对阵甲队时总体发挥较好 16 （2020南京二模）为了解九年级女生体质健康变化的情况，体育李老师本学期从九年级全体 240 名女 生中随机抽取 20 名女生进行体质测试，并调取这 20 名女生上学期的体质测试成绩进行对比，李老师对 两次数据（成绩）进行整理、描述和分析下面给出了部分信息 a两次测试成绩（百分制）的频数分布直方图如下（数据分组：60 x70，70 x80，80 x90， 90 x100） ： b成绩在 80 x90 的是： 上学期：80 81 85 85
40、85 86 88 本学期：80 82 83 86 86 86 88 89 c两个学期样本测试成绩的平均数、中位数、众数如下： 学期 平均数 中位数 众数 上学期 84 a 85 本学期 b c d 根据以上信息，回答下列问题： （1）表中 a 的值是 80.5 ； （2）下列关于本学期样本测试成绩的结论：c86；d86；成绩的极差可能为 41；b 有可能等 于 80其中所有正确结论的序号是 ； （3）从两个不同角度分析这 20 名女生从上学期到本学期体质健康变化情况 【答案】见试题解答内容 【解答】解： （1）80.5， 故答案为：80.5； （2）上学期成绩处在第 10、11 位的两个数都是
41、 86，因此中位数 c86，故正确； 平均数、众数受每组的具体数据的影响，因此不能确定，极差最大为 1006040，不能为 41，因此 不正确； 假设平均数是 80 分，则 20 人的总成绩为 80201600 分，而 8090 组的总分为 680 分，其它三个组 的总分为 1600680920 分， 而 603+703+906930920，因此平均分不能为 80 分； 故答案为：； （3）从中位数上看，由上学期的 80.5，到本学期的 86，一半以上的女生体质情况有较大提升； 从成绩达到 80 分的女生数上看，本学期比上学期增加 3 人，且 90 分以上多 2 人，体质训练有效果 17 （2
42、020鼓楼区二模）甲盒中有标号为 1，2，3 的牌子，乙盒中有标号为 1，2，3，4 的牌子，两个盒子 均不透明，这些牌子除标号外无其他差别小勇从甲盒中随机摸出一个牌子，标号为 a，小婷从乙盒中 随机摸出一个牌子，标号为 b，若 ab，则小勇获胜；若 ab，则小婷获胜 （1）求小勇获胜的概率； （ 2 ） 若 小 勇 摸 出 的 牌 子 标 号 为 2 ， 在 不 知 道 小 婷 标 号 的 情 况 下 ， 他 获 胜 的 概 率 是 【答案】见试题解答内容 【解答】解： （1）画树状图如图： 共有 12 个等可能的结果，小勇获胜的结果有 6 个， 小勇获胜的概率为； （2）若小勇摸出的牌子标
43、号为 2，在不知道小婷标号的情况下， 当抽出 3 或 4 时，小勇获胜， 当抽出 1 或 2 时，小婷获胜， 他获胜的结果有 2 个， 若小勇摸出的牌子标号为 2，在不知道小婷标号的情况下，他获胜的概率为； 故答案为： 18 （2020南京二模）经过某路口的汽车，可能直行，也可能向左转或向右转如果这三种可能性大小相 同，现有甲、乙、丙三辆汽车经过这个路口 （1）求甲、乙两辆汽车向同一方向行驶的概率； （2）甲、乙、丙三辆汽车向同一方向行驶的概率是 【答案】见试题解答内容 【解答】解： （1）根据题意画图如下： 共有 9 种等情况数，其中甲、乙两辆汽车向同一方向行驶的有 3 种， 则甲、乙两辆汽
44、车向同一方向行驶的概率是； （2）根据题意画图如下： 共有 27 种等情况数，其中甲、乙、丙三辆汽车向同一方向行驶的有 3 种， 则 P（三辆汽车朝一个方向行驶） 故答案为： 19 （2020建邺区一模）某校七、八、九年级共有 1000 名学生学校统计了各年级学生的人数，绘制了图 、图两幅不完整的统计图 （1）将图的条形统计图补充完整 （2）图中，表示七年级学生人数的扇形的圆心角度数为 144 （3）学校数学兴趣小组调查了各年级男生的人数，绘制了如图所示的各年级男生人数占比的折线统计 图（年级男生人数占比100%） 请结合相关信息，绘制一幅适当的统计图，表示 各年级男生及女生的人数，并在图中标
45、明相应的数据 【答案】见试题解答内容 【解答】解： （1）八年级人数：100025%250（人） ，七年级人数：1000250350400（人） ， 补全条形统计图如图所示： （2）360144 故答案为：144； （3）七年级：男生 40060%240 人，女生 400（160%）160 人， 八年级：男生 40050%125 人，女生 400（150%）125 人， 九年级：男生 35060%210 人，女生 400（160%）140 人， 用条形统计图表示如下： 20 （2020玄武区一模） 某班有甲、 乙两名同学报名参加 100 米跑步比赛， 他们在赛前进行了 10 次训练 将 两人的
46、 10 次训练成绩分别绘制成如图统计图 （1）根据统计图把下列表格补充完整： 平均数（s） 方差（s2） 跑进 15s 以内（不包括 15s）的占比 甲 15 0.07 50% 乙 15 0.038 40% （2）从两个不同角度评价甲、乙两名同学的训练成绩 【答案】见试题解答内容 【解答】解： （1）甲同学 10 次训练的成绩为：15.0，14.7，15.3，15.0，14.8，14.9，15.5，14.7，14.8， 15.3，平均数为 15， 所以方差为：2（14.715） 2+2（14.815）2+（14.915）2+2（15.015）2+2（15.315） 2+（15.515）20.0
47、7， 乙跑进 15s 以内（不包括 15s）的占比为：100%40% 故答案为：0.07，40%； （2）两人训练成绩的平均数都是 15s，说明两人成绩整体实力相当； 甲的方差大于乙的方差，说明乙的成绩更加稳定 或：甲跑进 15s 以内的占比多于乙，且甲的最快速度比乙快，说明甲更加有可能创造出好成绩 21 （2020秦淮区一模）面对今年的新冠疫情，某区所有中学开展了“停课不停学”活动该区教育主管 部门随机调查了一些家长对该活动的态度（A：无所谓；B：赞成；C：反对） ，并将调査结果绘制成图 和图的统计图请根据图中提供的信息，解答下列问题： （1）在图中，C 部分所占扇形的圆心角度数为 18 ；
48、 （2）将图补充完整； （ 3 ） 根 据 抽 样 调 查 结 果 ， 估 计 该 区 30000 名 中 学 生 家 长 中 有 多 少 人 持 赞 成 态 度 ？ 【答案】见试题解答内容 【解答】解： （1）由题意得：C 部分所占扇形的圆心角度数为 12（20485%）36018； 故答案为：18； （2）A：无所谓有 20485%2041224 人，将图补充完整如图所示， （3）3000085%25500（人） 答：估计该区 30000 名中学生家长中有 25500 人持赞成态度 22 （2020浦口区模拟）一个不透明的布袋中仅有 2 个红球、1 个黑球，这些球除颜色外无其他差别 （1）甲同学先随机摸出一个小球，记下颜色后放回搅匀，再随机摸出一个小球，则两次摸出的小球颜色 不同的概率是多少？ （2）乙同学从中一次摸出两个球，则摸出的小球均为红色的概率是 【答案】见试题解答内容 【解答】解： （1）画树状图如图所示： 一共有 9 种等可能的情况，两次摸出的小球颜色不同的有 4 种， 两次摸出的小球颜色不同的概率为； （2）由（1）可知一共有 9 种等可
