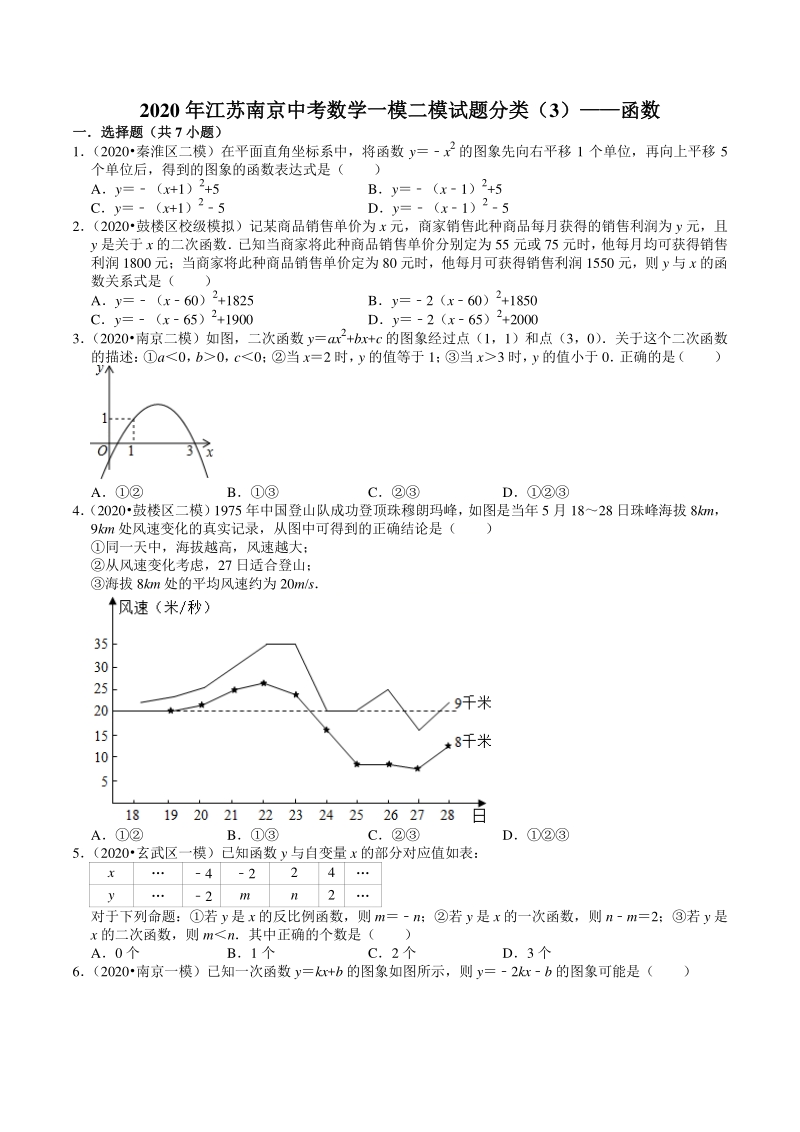
1、2020 年江苏年江苏南京南京中考数学一模二模试题分类（中考数学一模二模试题分类（3）函数函数 一选择题（共一选择题（共 7 小题）小题） 1 （2020秦淮区二模）在平面直角坐标系中，将函数 yx2的图象先向右平移 1 个单位，再向上平移 5 个单位后，得到的图象的函数表达式是（ ） Ay（x+1）2+5 By（x1）2+5 Cy（x+1）25 Dy（x1）25 2 （2020鼓楼区校级模拟）记某商品销售单价为 x 元，商家销售此种商品每月获得的销售利润为 y 元，且 y 是关于 x 的二次函数 已知当商家将此种商品销售单价分别定为 55 元或 75 元时， 他每月均可获得销售 利润 180
2、0 元；当商家将此种商品销售单价定为 80 元时，他每月可获得销售利润 1550 元，则 y 与 x 的函 数关系式是（ ） Ay（x60）2+1825 By2（x60）2+1850 Cy（x65）2+1900 Dy2（x65）2+2000 3 （2020南京二模）如图，二次函数 yax2+bx+c 的图象经过点（1，1）和点（3，0） 关于这个二次函数 的描述： a0， b0， c0； 当 x2 时， y 的值等于 1； 当 x3 时， y 的值小于 0 正确的是 （ ） A B C D 4 （2020鼓楼区二模） 1975 年中国登山队成功登顶珠穆朗玛峰， 如图是当年 5 月 1828 日
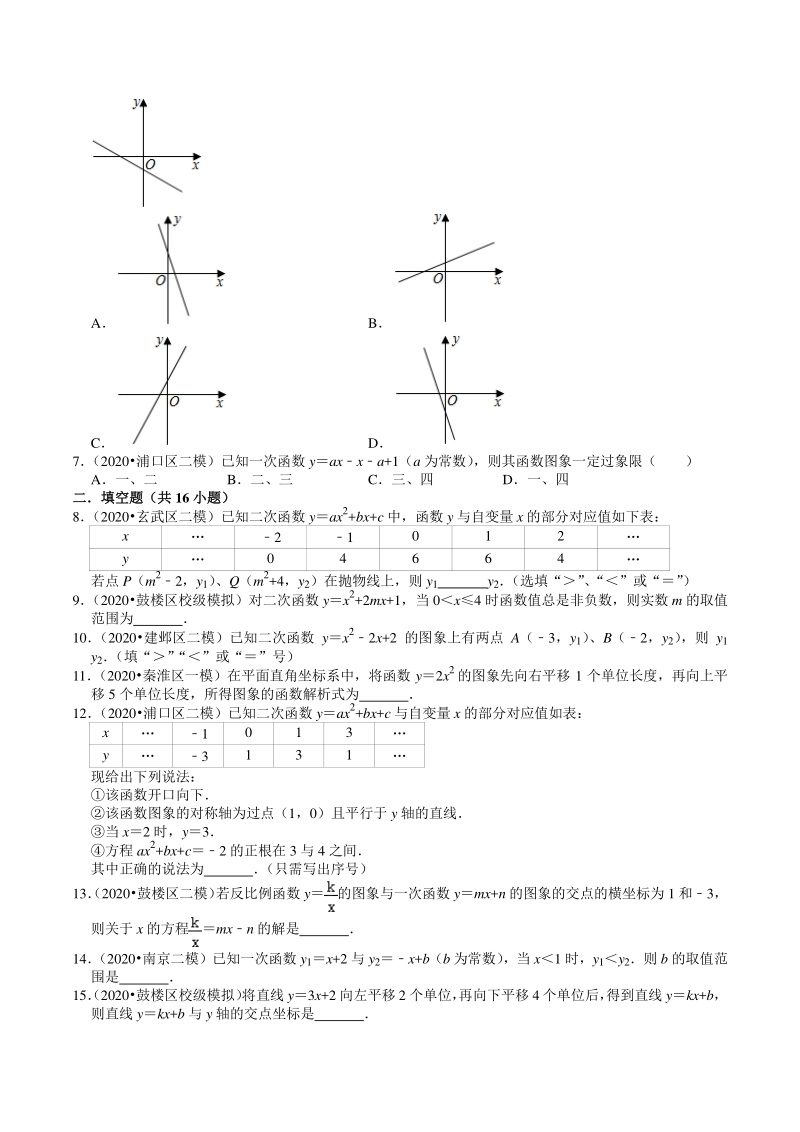
3、珠峰海拔 8km， 9km 处风速变化的真实记录，从图中可得到的正确结论是（ ） 同一天中，海拔越高，风速越大； 从风速变化考虑，27 日适合登山； 海拔 8km 处的平均风速约为 20m/s A B C D 5 （2020玄武区一模）已知函数 y 与自变量 x 的部分对应值如表： x 4 2 2 4 y 2 m n 2 对于下列命题：若 y 是 x 的反比例函数，则 mn；若 y 是 x 的一次函数，则 nm2；若 y 是 x 的二次函数，则 mn其中正确的个数是（ ） A0 个 B1 个 C2 个 D3 个 6 （2020南京一模）已知一次函数 ykx+b 的图象如图所示，则 y2kxb
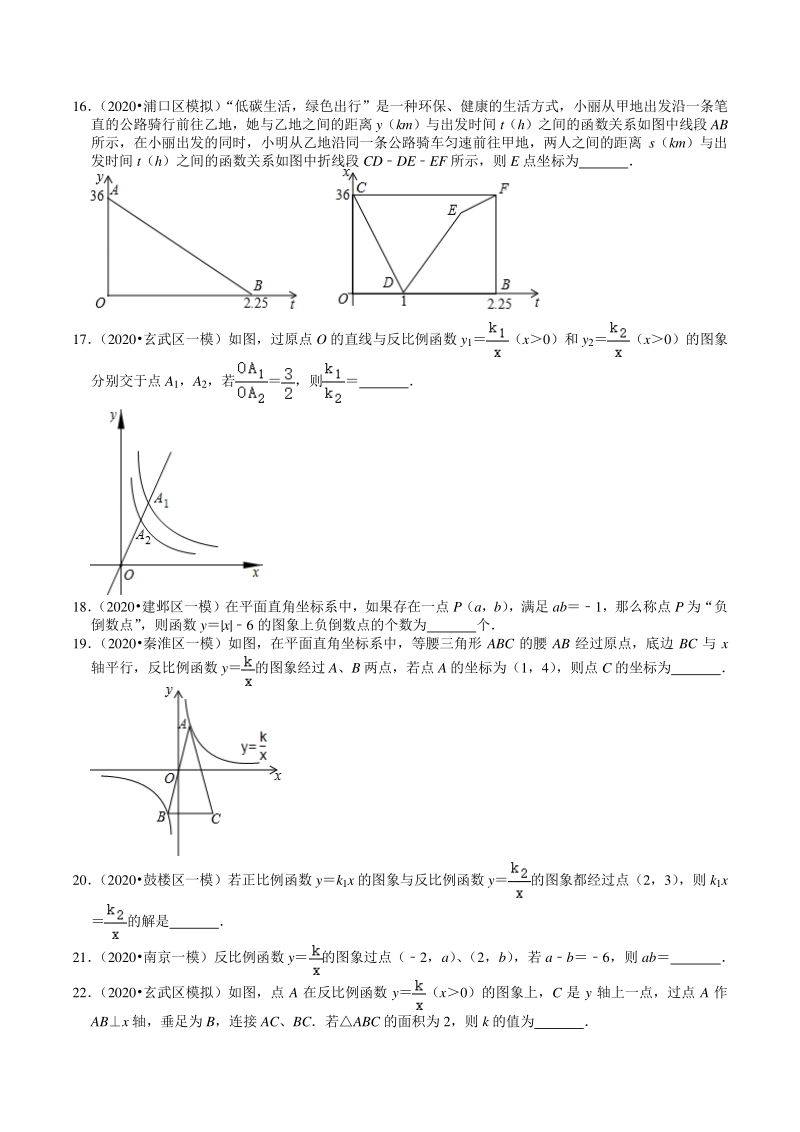
4、的图象可能是（ ） A B C D 7 （2020浦口区二模）已知一次函数 yaxxa+1（a 为常数） ，则其函数图象一定过象限（ ） A一、二 B二、三 C三、四 D一、四 二填空题（共二填空题（共 16 小题）小题） 8 （2020玄武区二模）已知二次函数 yax2+bx+c 中，函数 y 与自变量 x 的部分对应值如下表： x 2 1 0 1 2 y 0 4 6 6 4 若点 P（m22，y1） 、Q（m2+4，y2）在抛物线上，则 y1 y2 （选填“” 、 “”或“” ） 9 （2020鼓楼区校级模拟）对二次函数 yx2+2mx+1，当 0 x4 时函数值总是非负数，则实数 m 的
5、取值 范围为 10 （2020建邺区二模）已知二次函数 yx22x+2 的图象上有两点 A（3，y1） 、B（2，y2） ，则 y1 y2 （填“” “”或“”号） 11 （2020秦淮区一模）在平面直角坐标系中，将函数 y2x2的图象先向右平移 1 个单位长度，再向上平 移 5 个单位长度，所得图象的函数解析式为 12 （2020浦口区二模）已知二次函数 yax2+bx+c 与自变量 x 的部分对应值如表： x 1 0 1 3 y 3 1 3 1 现给出下列说法： 该函数开口向下 该函数图象的对称轴为过点（1，0）且平行于 y 轴的直线 当 x2 时，y3 方程 ax2+bx+c2 的正根在
6、 3 与 4 之间 其中正确的说法为 （只需写出序号） 13（2020鼓楼区二模） 若反比例函数 y的图象与一次函数 ymx+n 的图象的交点的横坐标为 1 和3， 则关于 x 的方程mxn 的解是 14 （2020南京二模）已知一次函数 y1x+2 与 y2x+b（b 为常数） ，当 x1 时，y1y2则 b 的取值范 围是 15（2020鼓楼区校级模拟） 将直线 y3x+2 向左平移 2 个单位， 再向下平移 4 个单位后， 得到直线 ykx+b， 则直线 ykx+b 与 y 轴的交点坐标是 16 （2020浦口区模拟） “低碳生活，绿色出行”是一种环保、健康的生活方式，小丽从甲地出发沿一
7、条笔 直的公路骑行前往乙地，她与乙地之间的距离 y（km）与出发时间 t（h）之间的函数关系如图中线段 AB 所示，在小丽出发的同时，小明从乙地沿同一条公路骑车匀速前往甲地，两人之间的距离 s（km）与出 发时间 t（h）之间的函数关系如图中折线段 CDDEEF 所示，则 E 点坐标为 17 （2020玄武区一模）如图，过原点 O 的直线与反比例函数 y1（x0）和 y2（x0）的图象 分别交于点 A1，A2，若，则 18 （2020建邺区一模）在平面直角坐标系中，如果存在一点 P（a，b） ，满足 ab1，那么称点 P 为“负 倒数点” ，则函数 y|x|6 的图象上负倒数点的个数为 个 1
8、9 （2020秦淮区一模）如图，在平面直角坐标系中，等腰三角形 ABC 的腰 AB 经过原点，底边 BC 与 x 轴平行，反比例函数 y的图象经过 A、B 两点，若点 A 的坐标为（1，4） ，则点 C 的坐标为 20 （2020鼓楼区一模）若正比例函数 yk1x 的图象与反比例函数 y的图象都经过点（2，3） ，则 k1x 的解是 21 （2020南京一模）反比例函数 y的图象过点（2，a） 、 （2，b） ，若 ab6，则 ab 22 （2020玄武区模拟）如图，点 A 在反比例函数 y（x0）的图象上，C 是 y 轴上一点，过点 A 作 ABx 轴，垂足为 B，连接 AC、BC若ABC
9、的面积为 2，则 k 的值为 23 （2020建邺区二模）函数 y中，自变量 x 的取值范围是 三解答题（共三解答题（共 23 小题）小题） 24 （2020玄武区二模）已知函数 ym（x1）2+2（x1） （m 为常数） （1）求证：无论 m 为何值，该函数的图象都经过 x 轴上的一个定点； （2）若该函数的图象与坐标轴交点的横、纵坐标均为整数，求 m 的值 25 （2020南京二模）已知二次函数 ym（x1） （xm3） （m 为常数，且 m0） （1）求证：不论 m 为何值，该函数的图象与 x 轴总有公共点； （2）设该函数的图象与 y 轴交于点 A，若点 A 在 x 轴上方，求 m 的
10、取值范围； （3）该函数图象所过的象限随 m 的值变化而变化，直接写出函数图象所经过的象限及对应的 m 的取值 范围 26 （2020鼓楼区二模）已知二次函数 yax26ax+5a（a 为常数，a0）的图象为抛物线 C （1）求证：不论 a 为何值，抛物线 C 与 x 轴总有两个不同的公共点； （2）设抛物线 C 交 x 轴于点 A、B，交 y 轴于点 D，若ABD 的面积为 20，求 a 的值； （3）设点 E（2，4） 、F（3，4） ，若抛物线 C 与线段 EF 只有一个公共点，结合函数图象，直接写出 a 的取值范围 27 （2020秦淮区一模）从“数”与“形”两个角度解决问题 1 和问
11、题 2 （1）问题 1 两数之和为 14，其中一个数比另一个数大 4，求这两个数 【 “数”的角度】 解：设较大数为 x，较小数为 y 根据题意，得，解这个方程组，得 【 “形”的角度】 解：设较大数为 x，较小数为 y 根据题意，得 y 与 x 的函数关系为 yx+14，yx4 在同一直角坐标系中画出它们的函数图象，得； 两个函数图象的交点坐标为 所以问题 1 的答案是 （2）问题 2 一根长 16cm 的铁丝能否围成面积为 12cm2的矩形？ 28 （2020玄武区一模）商家销售某种商品，每件成本 50 元经市场调研，当售价为 60 元时，可销售 300 件；售价每增加 1 元，销售量将减
12、少 10 件为了提高销售量，当售价为 80 元时，网络主播直播带货， 此时售价每增加 1 元，需支付给主播 300 元物价局对该商家聘请问此商品规定：售价最高不超过 110 元如图中的折线 ABC 表示该商品的销售量 y（单位：件）与售价 x（单位：元）之间的函数关系 （1）求线段 BC 对应的函数表达式； （2）当售价为多少元时，该商家获得的利润最大？最大利润是多少？ （3）直播带货后，售价至少为 元，该商家获得的利润不低于直播带货前的最大利润 29 （2020秦淮区一模）已知二次函数 y（xk）2+2（xk） （k 为常数） （1）该函数的图象与 x 轴有 个公共点； （2）在该函数的图象
13、上任取两点 A（2k，y1） ，B（2k+1，y2） ，试比较 y1与 y2的大小 30 （2020建邺区一模）已知函数 yx2+（m3）x+12m（m 为常数） （1）求证：不论 m 为何值，该函数的图象与 x 轴总有两个公共点 （2）不论 m 为何值，该函数的图象都会经过一个定点，求定点的坐标 31 （2020鼓楼区一模）已知 y 是 x 的二次函数，该函数的图象经过点 A（0，5） 、B（1，2） 、C（3，2） （1）求该二次函数的表达式，画出它的大致图象并标注顶点及其坐标； （2）结合图象，回答下列问题： 当 1x4 时，y 的取值范围是 ； 当 mxm+3 时，求 y 的最大值（用
14、含 m 的代数式表示） ； 是否存在实数 m、n（mn） ，使得当 mxn 时，myn？若存在，请求出 m、n；若不存在，请说 明理由 32 （2020玄武区模拟）已知二次函数 yx22mx+2m21（m 为常数） （1）若该函数图象与 x 轴只有一个公共点，求 m 的值 （2）将该函数图象沿过其顶点且平行于 x 轴的直线翻折，得到新函数图象 则新函数的表达式为 ，并证明新函数图象始终经过一个定点； 已知点 A（2，1） 、B（2，1） ，若新函数图象与线段 AB 只有一个公共点，请直接写出 m 的取值 范围 33 （2020南京一模）已知二次函数 yx22mx+m2+m1（m 是常数） （1
15、）求证：不论 m 为何值，该函数图象的顶点都在函数 yx1 的图象上 （2）若该函数图象与函数 yx+b 的图象有两个交点，则 b 的取值范围为（ ） Ab0；Bb1；Cb；Db2 （3）该函数图象与坐标轴交点的个数随 m 的值变化而变化，直接写出交点个数及对应的 m 取值范围 34 （2020浦口区模拟）在平面直角坐标系 xOy 中，已知抛物线 yx2mx+n （1）当 m2 时， 求抛物线的对称轴，并用含 n 的式子表示顶点的纵坐标； 若点 A（2，y1） ，B（x2，y2）都在抛物线上，且 y2y1，则 x2的取值范围是 ； （2）已知点 P（1，2） ，将点 P 向右平移 4 个单位长
16、度，得到点 Q当 n3 时，若抛物线与线段 PQ 恰有一个公共点，结合函数图象，求 m 的取值范围 35 （2020南京二模）某商场经市场调查，发现进价为 40 元的某童装每月的销售量 y（件）与售价 x（元） 的相关信息如下： 售价 x（元） 60 70 80 90 销售量 y（件） 280 260 240 220 （1）试用你学过的函数来描述 y 与 x 的关系，这个函数可以是 （填一次函数、反比例函数或二 次函数） ，求这个函数关系式； （2）售价为多少元时，当月的利润最大？最大利润是多少？ 36 （2020浦口区二模）把一根长 80cm 的铁丝分成两个部分，分别围成两个正方形 （1）能
17、否使所围的两个正方形的面积和为 250cm2，并说明理由； （2）能否使所围的两个正方形的面积和为 180cm2，并说明理由； （3）怎么分，使围成两个正方形的面积和最小？ 37 （2020秦淮区二模）用充电器给某手机充电时，其屏幕的起始画面如图 经测试，在用快速充电器和普通充电器对该手机充电时，其电量 E（单位：%）与充电时间 t（单位：h） 的函数图象分别为图中的线段 AB、AC （1）求线段 AB、AC 对应的函数表达式； （2）已知该手机正常使用时耗电量为 10%/h，在用快速充电器将其充满电后，正常使用 ah，接着再用普 通充电器将其充满电，其“充电耗电充电”的时间恰好是 6h，求
18、a 的值 38 （2020南京二模）某观光湖风景区，一观光轮与一巡逻艇同时从甲码头出发驶往乙码头，巡逻艇匀速 往返于甲、 乙两个码头之间， 当观光轮到达乙码头时， 巡逻艇也同时到达乙码头 设出发 xh 后， 观光轮、 巡逻艇离甲码头的距离分别为 y1km、y2km图中的线段 OG、折线 OABCDEFG 分别表示 y1、y2与 x 之 间的函数关系 （1）观光轮的速度是 km/h，巡逻艇的速度是 km/h； （2）求整个过程中观光轮与巡逻艇的最大距离； （3）求整个过程中观光轮与巡逻艇相遇的最短时间间隔 39 （2020玄武区一模）已知一次函数 y12x+m（m 为常数）和 y2x+1 （1）
19、当 m2 时，若 y1y2，求 x 的取值范围； （2）当 x11 时，y1y2；当 x11 时，y1y2，则 m 的值是 （3）判断函数 yy1y2的图象与 x 轴的交点个数情况，并说明理由 40 （2020建邺区一模）已知一次函数 y1kx2（k 为常数，k0）和 y2x+1 （1）当 k3 时，若 y1y2，求 x 的取值范围 （2）在同一平面直角坐标系中，若两函数的图象相交所形成的锐角小于 15，请直接写出 k 的取值范 围 41 （2020鼓楼区一模）某工厂生产 A、B、C 三种产品，这三种产品的生产数量均为 x 件它们的单件成 本和固定成本如表： 产品 单件成本（元/件） 固定成本
20、（元） A 0.1 1100 B 0.8 a C b（b0） 200 （注：总成本单件成本生产数量+固定成本） （1）若产品 A 的总成本为 yA，则 yA关于 x 的函数表达式为 （2）当 x1000 时，产品 A、B 的总成本相同 求 a； 当 x2000 时，产品 C 的总成本最低，求 b 的取值范围 42 （2020南京一模）一辆货车从 A 地出发以每小时 80km 的速度匀速驶往 B 地，一段时间后，一辆轿车从 B 地出发沿同一条路匀速驶往 A 地货车行驶 3 小时后，在距 B 地 160km 处与轿车相遇图中线段表示 货车离 B 地的距离 y1与货车行驶的时间 x 的关系 （1）A
21、B 两地之间的距离为 km； （2）求 y1与 x 之间的函数关系式； （3）若两车同时到达各自目的地，在同一坐标系中画出轿车离 B 地的距离 y2与货车行驶时间 x 的函数 图象，用文字说明该图象与 x 轴交点所表示的实际意义 43 （2020玄武区模拟）甲、乙两人从 M 地出发，甲先出发，乙后出发，都匀速骑车前往 N 地乙在骑行 途中休息片刻后，以原速度继续骑行已知乙的速度是甲的 1.6 倍甲、乙两人离 M 地的距离（米）与 乙行驶的时间 x（分钟）之间的关系如图，请根据图象回答问题 （1）M、N 两地之间的距离为 米，甲的速度为 米/分钟 （2）求线段 BD 所表示的 y 与 x 之间的
22、函数表达式 （3）直接写出当 x 取何值时，甲、乙两人在到达 N 地之前相遇 44 （2020鼓楼区校级模拟）如图，在平面直角坐标系中，直线 AB：ykx+4（k0）与 x 轴，y 轴，交于 A、B 两点，点 C 是 BO 的中点且 tanABO （1）求直线 AC 的解析式； （2）若点 M 是直线 AC 的一点，当 SABM2SAOC时，求点 M 的坐标 45（2020浦口区二模） 如图， 正比例函数 y2x 的图象与反比例函数 y的图象交于点 A、 B， AB2， （1）求 k 的值； （2）若反比例函数 y的图象上存在一点 C，则当ABC 为直角三角形，请直接写出点 C 的坐标 46
23、（2020建邺区二模）小王骑车从甲地到乙地，小李骑车从乙地到甲地，两人同时出发，沿同一条公路 匀速前进，在出发 2h 时，两人相距 36km，在出发 3h 时，两人相遇设骑行的时间为 x（h） ，两人之间 的距离为 y（km） ，图中的线段 AB 表示两人从出发到相遇这个过程中，y 与 x 之间的函数关系 （1）求线段 AB 所表示的 y 与 x 之间的函数表达式； （2）求甲、乙两地之间的距离 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 7 小题）小题） 1 （2020秦淮区二模）在平面直角坐标系中，将函数 yx2的图象先向右平移 1 个单位，再向上平移 5 个单位后，得
24、到的图象的函数表达式是（ ） Ay（x+1）2+5 By（x1）2+5 Cy（x+1）25 Dy（x1）25 【答案】B 【解答】解：函数 yx2的图象先向右平移 1 个单位，再向上平移 5 个单位， 平移后的抛物线的顶点坐标为（1，5） ， 平移后得到的函数关系式为 y（x1）2+5 故选：B 2 （2020鼓楼区校级模拟）记某商品销售单价为 x 元，商家销售此种商品每月获得的销售利润为 y 元，且 y 是关于 x 的二次函数 已知当商家将此种商品销售单价分别定为 55 元或 75 元时， 他每月均可获得销售 利润 1800 元；当商家将此种商品销售单价定为 80 元时，他每月可获得销售利润
25、 1550 元，则 y 与 x 的函 数关系式是（ ） Ay（x60）2+1825 By2（x60）2+1850 Cy（x65）2+1900 Dy2（x65）2+2000 【答案】D 【解答】解：设二次函数的解析式为：yax2+bx+c， 当 x55，75，80 时，y1800，1800，1550， ， 解得， y 与 x 的函数关系式是 y2x2+260 x64502（x65）2+2000， 故选：D 3 （2020南京二模）如图，二次函数 yax2+bx+c 的图象经过点（1，1）和点（3，0） 关于这个二次函数 的描述： a0， b0， c0； 当 x2 时， y 的值等于 1； 当 x
26、3 时， y 的值小于 0 正确的是 （ ） A B C D 【答案】B 【解答】解：如图所示，抛物线开口方向向下，则 a0 对称轴在 y 轴的右侧，则 a、b 异号，即 b0 抛物线与 y 轴交于负半轴，则 b0 综上所述，a0，b0，c0 故正确； 抛物线与 x 轴另一交点横坐标 0 x1， 抛物线的顶点横坐标x2 抛物线开口向下，且过点（1，1） ， 点（1，1）关于对称轴对称的点的横坐标大于 2， 当 x2 时，y 的值大于 1，故错误； 观察函数图象，可知：当 x3 时，y 的值小于 0， 故正确； 故选：B 4 （2020鼓楼区二模） 1975 年中国登山队成功登顶珠穆朗玛峰， 如
27、图是当年 5 月 1828 日珠峰海拔 8km， 9km 处风速变化的真实记录，从图中可得到的正确结论是（ ） 同一天中，海拔越高，风速越大； 从风速变化考虑，27 日适合登山； 海拔 8km 处的平均风速约为 20m/s A B C D 【答案】A 【解答】解：同一天中，海拔越高，风速越大，说法正确； 从风速变化考虑，27 日适合登山，说法正确； 海拔 8km 处的平均风速约为 15m/s，说法错误； 故选：A 5 （2020玄武区一模）已知函数 y 与自变量 x 的部分对应值如表： x 4 2 2 4 y 2 m n 2 对于下列命题：若 y 是 x 的反比例函数，则 mn；若 y 是 x
28、 的一次函数，则 nm2；若 y 是 x 的二次函数，则 mn其中正确的个数是（ ） A0 个 B1 个 C2 个 D3 个 【答案】D 【解答】解：若 y 是 x 的反比例函数，则2m2n42， 解得 m4，n4，则 mn，故正确； 若 y 是 x 的一次函数，设为 ykx+b， 把 x4，y2；x4，y2 代入求得 yx， 当 x2 时 y1；x2 时 y1， m1，n1， nm2，故正确； 若 y 是 x 的二次函数，由函数经过点（4，2）和（4，2） ， 当开口向上时，对称轴在 y 轴的左侧，则点（2，m）到对称轴的距离小于点（2，n）到对称轴的距离， 所以 mn； 当开口向下时，对称
29、轴在 y 轴的右侧，则点（2，m）到对称轴的距离大于点（2，n）到对称轴的距离， 所以 mn； 故正确； 故选：D 6 （2020南京一模）已知一次函数 ykx+b 的图象如图所示，则 y2kxb 的图象可能是（ ） A B C D 【答案】C 【解答】解：一次函数 ykx+b 的图象经过二、三、四象限， k0，b0 函数 y2kb 的图象经过第一、二、三象限 因为|k|2k|， 所以一次函数 ykx+b 的图象比 y2kxb 的图象的倾斜度小， 综上所述，符合条件的图象是 C 选项 故选：C 7 （2020浦口区二模）已知一次函数 yaxxa+1（a 为常数） ，则其函数图象一定过象限（ ）
30、 A一、二 B二、三 C三、四 D一、四 【答案】D 【解答】解：一次函数 yaxxa+1（a1）x（a1） ， 当 a10 时，（a1）0，图象经过一、三、四象限； 当 a10 时，（a1）0，图象经过一、二、四象限； 所以其函数图象一定过一、四象限， 故选：D 二填空题（共二填空题（共 16 小题）小题） 8 （2020玄武区二模）已知二次函数 yax2+bx+c 中，函数 y 与自变量 x 的部分对应值如下表： x 2 1 0 1 2 y 0 4 6 6 4 若点 P（m22，y1） 、Q（m2+4，y2）在抛物线上，则 y1 y2 （选填“” 、 “”或“” ） 【答案】 【解答】解：
31、x0 时，y6；x1 时，y6， 抛物线的对称轴为直线 x，且抛物线开口向下， 点 P（m22，y1） 、Q（m2+4，y2）在抛物线上，且|m22|m2+4|， y1y2， 故答案为 9 （2020鼓楼区校级模拟）对二次函数 yx2+2mx+1，当 0 x4 时函数值总是非负数，则实数 m 的取值 范围为 m1 【答案】见试题解答内容 【解答】解：对称轴为：， 分三种情况：当对称轴 x0 时，即m0，m0，满足当 0 x4 时的函数值总是非负数； 当时，0m4，4m0，当 1m20 时，1m1，满足当 0 x4 时的函数 值总是非负数； 当 1m20 时，不能满足当 0 x4 时的函数值总是
32、非负数； 当1m0 时，当 0 x4 时的函数值总是非负数， 当对称轴m4，即 m4，如果满足当 0 x4 时的函数值总是非负数，则有 x4 时，y0， 16+8m+10， m，此种情况 m 无解； 综合可得：当 m1 时，当 0 x4 时函数值总是非负数 10 （2020建邺区二模）已知二次函数 yx22x+2 的图象上有两点 A（3，y1） 、B（2，y2） ，则 y1 y2 （填“” “”或“”号） 【答案】见试题解答内容 【解答】解：二次函数 yx22x+2 的对称轴是 x1，开口向上， 在对称轴的左侧 y 随 x 的增大而减小， 点 A（3，y1） ，B（2，y2）是二次函数 yx2
33、2x+2 的图象上的两点， 23， y1y2 故答案为： 11 （2020秦淮区一模）在平面直角坐标系中，将函数 y2x2的图象先向右平移 1 个单位长度，再向上平 移 5 个单位长度，所得图象的函数解析式为 y2（x1）2+5 【答案】见试题解答内容 【解答】解：由“左加右减”的原则可知， 抛物线 y2x2的图象向右平移 1 个单位所得函数图象的关系式是：y2（x1）2； 由“上加下减”的原则可知， 抛物线 y2（x1）2的图象向上平移 5 个单位长度所得函数图象的关系式是：y2（x1）2+5 故答案为 y2（x1）2+5 12 （2020浦口区二模）已知二次函数 yax2+bx+c 与自变
34、量 x 的部分对应值如表： x 1 0 1 3 y 3 1 3 1 现给出下列说法： 该函数开口向下 该函数图象的对称轴为过点（1，0）且平行于 y 轴的直线 当 x2 时，y3 方程 ax2+bx+c2 的正根在 3 与 4 之间 其中正确的说法为 （只需写出序号） 【答案】见试题解答内容 【解答】解：二次函数值先由小变大，再由大变小， 抛物线的开口向下，所以正确； 抛物线过点（0，1）和（3，1） ， 抛物线的对称轴为直线 x，所以错误； 点（1，3）和点（2，3）为对称点，所以正确； x1 时，y3， x4 时，y3， 二次函数 yax2+bx+c 的函数值为2 时，1x0 或 3x4，
35、 即方程 ax2+bx+c2 的负根在1 与 0 之间，正根在 3 与 4 之间，所以正确 故答案为 13（2020鼓楼区二模） 若反比例函数 y的图象与一次函数 ymx+n 的图象的交点的横坐标为 1 和3， 则关于 x 的方程mxn 的解是 x11，x23 【答案】见试题解答内容 【解答】解：两交点坐标为（1，k） ， （3，k） ， 把（1，k） ， （3，k）代入 ymx+n 得，解得， 关于 x 的方程mxn 化为kxk，解得 x11，x23 即关于 x 的方程mxn 的解是 x11，x23 故答案为 x11，x23 14 （2020南京二模）已知一次函数 y1x+2 与 y2x+b
36、（b 为常数） ，当 x1 时，y1y2则 b 的取值范 围是 b4 【答案】见试题解答内容 【解答】解：解方程组得， 两函数图象的交点坐标为（，） ， 当 x1 时，y1y2， 1， b4 故答案为 b4 15（2020鼓楼区校级模拟） 将直线 y3x+2 向左平移 2 个单位， 再向下平移 4 个单位后， 得到直线 ykx+b， 则直线 ykx+b 与 y 轴的交点坐标是 （0，4） 【答案】见试题解答内容 【解答】解：将直线 y3x+2 向左平移 2 个单位，得到直线 y3（x+2）+2，即 y3x+8， 再向下平移 4 个单位，所得的解析式为 y3x+84，即 y3x+4， 令 x0，
37、则 y4， 直线 ykx+b 与 y 轴的交点坐标是（0，4） 故答案为（0，4） 16 （2020浦口区模拟） “低碳生活，绿色出行”是一种环保、健康的生活方式，小丽从甲地出发沿一条笔 直的公路骑行前往乙地，她与乙地之间的距离 y（km）与出发时间 t（h）之间的函数关系如图中线段 AB 所示，在小丽出发的同时，小明从乙地沿同一条公路骑车匀速前往甲地，两人之间的距离 s（km）与出 发时间 t（h）之间的函数关系如图中折线段 CDDEEF 所示，则 E 点坐标为 （，） 【答案】见试题解答内容 【解答】解：由图可得， 小丽的速度为：362.2516（km/h） ， 小明的速度为：361162
38、0（km/h） ， 故点 E 的横坐标为：3620，纵坐标是： （20+16）（1）， 故答案为： （，） 17 （2020玄武区一模）如图，过原点 O 的直线与反比例函数 y1（x0）和 y2（x0）的图象 分别交于点 A1，A2，若，则 【答案】见试题解答内容 【解答】解：分别过点 A1、A2作 x 轴的垂线，垂足分别为 M、N， 则OA1NOA2M， ，即两个三角形的相似比为 3：2， 则OA2M 和OA1N 的面积比为：9：4， 而， 故答案为： 18 （2020建邺区一模）在平面直角坐标系中，如果存在一点 P（a，b） ，满足 ab1，那么称点 P 为“负 倒数点” ，则函数 y|x
39、|6 的图象上负倒数点的个数为 3 个 【答案】见试题解答内容 【解答】解：ab1， b，且 a0，b0， 把（a，b）代入 y|x|6 得：|a|6， 当 a0 时，a6， a26a+10， 解得：a13+2，a232 当 a3+2时，b23，即 P（3+2，23） ； 当 a32时，b23，即 P（32，23） ； 当 a0 时，a6， a2+6a10， 解得：a13+，a23， 3， 30，即3+0， a13+不符合题意，舍去； 当 a3时，b3，即 P（3，3） 故答案为：3 19 （2020秦淮区一模）如图，在平面直角坐标系中，等腰三角形 ABC 的腰 AB 经过原点，底边 BC 与
40、 x 轴平行，反比例函数 y的图象经过 A、B 两点，若点 A 的坐标为（1，4） ，则点 C 的坐标为 （3， 4） 【答案】见试题解答内容 【解答】解：作 ADBC 于 D， BC 等腰三角形 ABC 的底边， CDBD， 反比例函数 y的图象经过 A、B 两点，若点 A 的坐标为（1，4） ， B（1，4） ， D（1，4） ， BD2， CDBD2， C（3，4） ， 故答案为（3，4） 20 （2020鼓楼区一模）若正比例函数 yk1x 的图象与反比例函数 y的图象都经过点（2，3） ，则 k1x 的解是 2 或2 【答案】见试题解答内容 【解答】解：两个函数的图象都经过点（2，3）
41、 ，即 k1x的一个解为 x12， 根据正比例函数点的对称性，则另外一个解为 x22， 故答案为 2 或2 21 （2020南京一模）反比例函数 y的图象过点（2，a） 、 （2，b） ，若 ab6，则 ab 9 【答案】见试题解答内容 【解答】解：反比例函数 y的图象过点（2，a） 、 （2，b） ， 2a2b， a+b0， ab6， a3，b3， ab9， 故答案为：9 22 （2020玄武区模拟）如图，点 A 在反比例函数 y（x0）的图象上，C 是 y 轴上一点，过点 A 作 ABx 轴，垂足为 B，连接 AC、BC若ABC 的面积为 2，则 k 的值为 4 【答案】见试题解答内容 【
42、解答】解：连结 OA，如图， ABx 轴， OCAB， SOABSABC2， 而 SOAB|k|， |k|2， k0， k4 故答案为 4 23 （2020建邺区二模）函数 y中，自变量 x 的取值范围是 x1 【答案】见试题解答内容 【解答】解：由题意，得 1x0， 解得 x1， 故答案为：x1 三解答题（共三解答题（共 23 小题）小题） 24 （2020玄武区二模）已知函数 ym（x1）2+2（x1） （m 为常数） （1）求证：无论 m 为何值，该函数的图象都经过 x 轴上的一个定点； （2）若该函数的图象与坐标轴交点的横、纵坐标均为整数，求 m 的值 【答案】 （1）证明过程见解析部
43、分； （2）m2，1，0，1，2 【解答】 （1）证明：当 m0 时，该函数是一次函数 y2x2，其函数图象与 x 轴交点坐标是（1，0） ； 当 m0 时，ym（x1）2+2（x1）（x1）m（x1）+2， 该抛物线与 x 轴交点横坐标分别是 1 和 1 无论 m 取何值，该抛物线与 x 轴总交于点（1，0） ； （2）解：若 m0，则 y2x2，此时函数与 x 轴，y 轴交点分别是（1，0） ， （0，2） ，符合题意； 若 m0 时，则函数与 x 轴交点分别是（1，0） ， （1，0） ，与 y 轴交点是（0，m2） 即当 m2 是整数时，1也是整数， 所以 m1，2 综上所述，m2，1
44、，0，1，2 25 （2020南京二模）已知二次函数 ym（x1） （xm3） （m 为常数，且 m0） （1）求证：不论 m 为何值，该函数的图象与 x 轴总有公共点； （2）设该函数的图象与 y 轴交于点 A，若点 A 在 x 轴上方，求 m 的取值范围； （3）该函数图象所过的象限随 m 的值变化而变化，直接写出函数图象所经过的象限及对应的 m 的取值 范围 【答案】见试题解答内容 【解答】 （1）证明：当 y0 时，m（x1） （xm3）0，解得 x11，x2m+3， 当 m+31，即 m2 时，方程有两个相等的实数根； 当 m+31，即 m2 时，方程有两个不相等的实数根， 不论 m
45、 为何值，该函数的图象与 x 轴总有公共点； （2）解：当 x0 时，ym2+3m， 点 A 坐标为（0，m2+3m） ， 该函数的图象与 y 轴交于点 A，点 A 在 x 轴上方， m2+3m0 设 zm2+3m，即 z 是 m 的二次函数，当 m0 或3 时，z0 抛物线开口向上， 当 m0 或 m3 时，z0 m 的取值范围是 m0 或 m3； （3）当 m0 时，图象经过一、二、四象限； 当3m0（m2）时，图象经过一、三、四象限； 当 m2 时，图象经过三、四象限； 当 m3 时，图象经过一、二、三、四象限 26 （2020鼓楼区二模）已知二次函数 yax26ax+5a（a 为常数，
46、a0）的图象为抛物线 C （1）求证：不论 a 为何值，抛物线 C 与 x 轴总有两个不同的公共点； （2）设抛物线 C 交 x 轴于点 A、B，交 y 轴于点 D，若ABD 的面积为 20，求 a 的值； （3）设点 E（2，4） 、F（3，4） ，若抛物线 C 与线段 EF 只有一个公共点，结合函数图象，直接写出 a 的取值范围 【答案】见试题解答内容 【解答】解： （1）a0， （6a）24a5a16a20， 故抛物线 C 与 x 轴总有两个不同的公共点； （2）对于 yax26ax+5a，令 y0，则 x1 或 5，令 x0，则 y5a， 故点 A、B、D 的坐标分别为： （1，0）
47、、 （5，0） 、 （0，5a） ， ABD 的面积AB|yD|45|a|20， 解得：a2； （3）当 a0 时，如图 1，EF 与抛物线不可能有公共点； 当 a0 时，如图 2， 临界点为点 E、F， 当抛物线过点 E 时，即 x2，yax26ax+5a3a4，解得：a， 当抛物线过点 F 时，即 x3，yax26ax+5a4a4，解得：a1， 故 a 的取值范围为a1 27 （2020秦淮区一模）从“数”与“形”两个角度解决问题 1 和问题 2 （1）问题 1 两数之和为 14，其中一个数比另一个数大 4，求这两个数 【 “数”的角度】 解：设较大数为 x，较小数为 y 根据题意，得，解
48、这个方程组，得 【 “形”的角度】 解：设较大数为 x，较小数为 y 根据题意，得 y 与 x 的函数关系为 yx+14，yx4 在同一直角坐标系中画出它们的函数图象，得； 两个函数图象的交点坐标为 （9，5） 所以问题 1 的答案是 9 和 5 （2）问题 2 一根长 16cm 的铁丝能否围成面积为 12cm2的矩形？ 【答案】见试题解答内容 【解答】解： （1）解方程组得：， 画出函数大致图象如下： 从图象看，两个函数的交点为（9，5） ； 故：这两个数分别为 9 和 5； 故答案为：， （9，5） ，9 和 5； （2） 【 “数”的角度】 方法一：设这根铁丝围成的矩形的一边长为 xcm 根据题意，得 x（8x）12 解这个方程，得 x16，x22 当 x16 时，8x12；当 x22 时，8x26 答：一根长 16cm 的铁丝能围成面积为 12cm2的矩形 方法二：设铁丝围成的矩形一边长为 xcm，相邻的另一边为 ycm 根据题意，得，解得或， 答：一根长 16cm 的铁丝能围成面积为 12cm2的矩形 【 “形”的角度】 方法一：设铁丝围成的矩形面积为 ycm2，一边长为 xcm 根据题意，得 y
