1、四校 2020 秋学期 八年级数学 第 1 次学情调查 试题 共 4 页 第 1 页 四校四校 20202021 学年度第一学期第学年度第一学期第 1 次学情调查次学情调查 八八年级数学试题年级数学试题 （考试时间：120 分钟，满分：150 分） 成绩_ 一选择题（共 6 小题，共 18 分） 1低碳环保理念深入人心，共享单车已成为出行新方式下列共享单车图标，是轴对标图形的是（ ） A B C D 2如图，某同学把一块三角形的玻璃打破成了三块，现要到玻璃店去配一块大小、形状完全相同的玻璃， 那么他可以（ ） A带去 B带去 C带去 D带和去 3小明从镜子中看到对面电子钟示数如图所示，这时的时
2、刻应是（ ） A21：10 B10：21 C10：51 D12：01 第 2 题 第 3 题 第 4 题 第 5 题 4如图，工人师傅砌门时，常用木条 EF 固定矩形门框 ABCD，使其不变形，这种做法的根据是（ ） A两点之间线段最短 B矩形的对称性 C矩形的四个角都是直角 D三角形的稳定性 5如图，OP 平分MON，PAON 于点 A，点 Q 是射线 OM 上的一个动点，若 PA2，则 PQ 的最小值为 （ ） A1 B2 C3 D4 6已知ABCABC，A40，CBA60，AC 交边 AB 于 P（点 P 不与 A、B 重合） BO、CO 分别平分CBA，BCP，若 mBOCn，则 nm
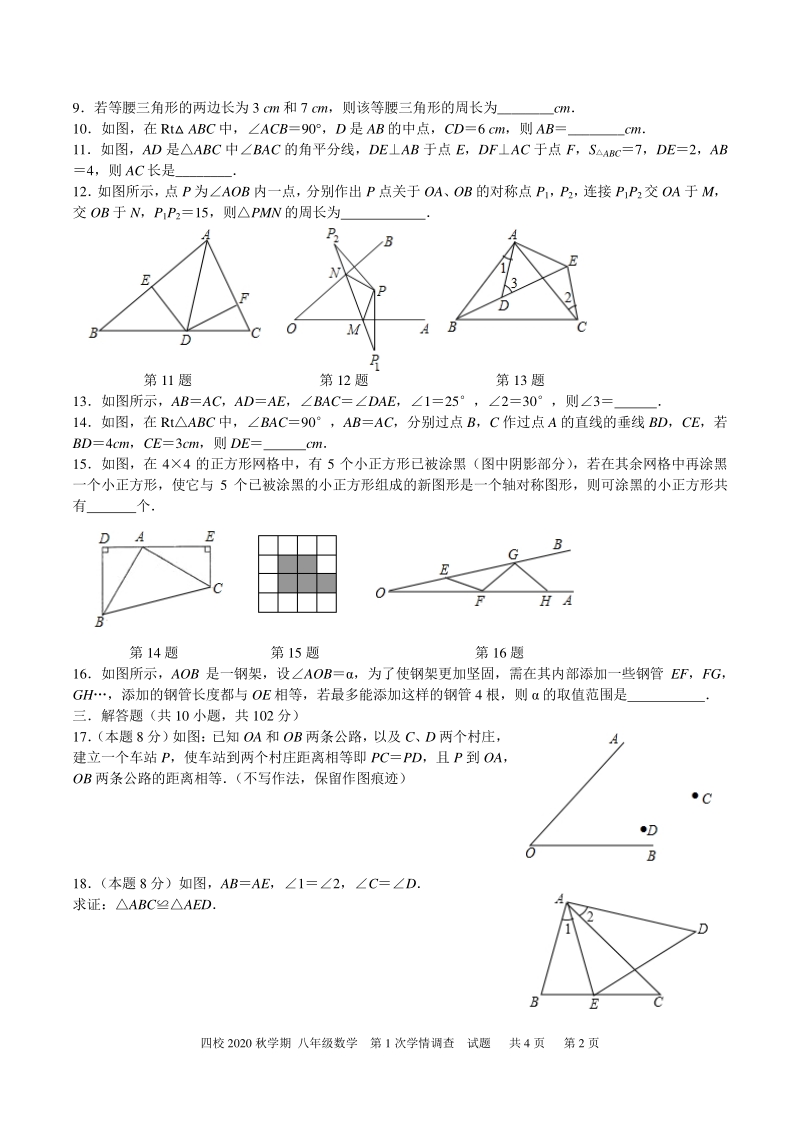
3、 的值为（ ） A20 B40 C60 D100 第 6 题 第 8 题 第 10 题 二填空题（共 10 小题，共 30 分） 7已知ABCABC，A60，B40，则C 8已知，如图：ABCDEF，ABDE，要说明ABCDEF，若以“ASA”为依据，还要添加的条 件为 D B A C O P BA B C A 四校 2020 秋学期 八年级数学 第 1 次学情调查 试题 共 4 页 第 2 页 9若等腰三角形的两边长为 3 cm 和 7 cm，则该等腰三角形的周长为_cm 10如图，在 Rt ABC 中，ACB90 ，D 是 AB 的中点，CD6 cm，则 AB_cm 11如图，AD 是AB
4、C 中BAC 的角平分线，DEAB 于点 E，DFAC 于点 F，SABC7，DE2，AB 4，则 AC 长是_ 12 如图所示， 点 P 为AOB 内一点， 分别作出 P 点关于 OA、 OB 的对称点 P1， P2， 连接 P1P2交 OA 于 M， 交 OB 于 N，P1P215，则PMN 的周长为 第 11 题 第 12 题 第 13 题 13如图所示，ABAC，ADAE，BACDAE，125，230，则3 14如图，在 RtABC 中，BAC90，ABAC，分别过点 B，C 作过点 A 的直线的垂线 BD，CE，若 BD4cm，CE3cm，则 DE cm 15如图，在 44 的正方形
5、网格中，有 5 个小正方形已被涂黑（图中阴影部分） ，若在其余网格中再涂黑 一个小正方形，使它与 5 个已被涂黑的小正方形组成的新图形是一个轴对称图形，则可涂黑的小正方形共 有 个 第 14 题 第 15 题 第 16 题 16如图所示，AOB 是一钢架，设AOB，为了使钢架更加坚固，需在其内部添加一些钢管 EF，FG， GH，添加的钢管长度都与 OE 相等，若最多能添加这样的钢管 4 根，则 的取值范围是 三解答题（共 10 小题，共 102 分） 17 （本题 8 分） 如图： 已知 OA 和 OB 两条公路， 以及 C、 D 两个村庄， 建立一个车站 P，使车站到两个村庄距离相等即 PC
6、PD，且 P 到 OA， OB 两条公路的距离相等 （不写作法，保留作图痕迹） 18 （本题 8 分）如图，ABAE，12，CD 求证：ABCAED 四校 2020 秋学期 八年级数学 第 1 次学情调查 试题 共 4 页 第 3 页 19 （本题 8 分）如图，点 B、E、C、F 在同一条直线上，AD，BDEF，BECF求证：AC DF 20 （本题 10 分）已知：如图ABCADC90，M、N 分别是 AC、BD 的中点求证：MNBD 21 （本题 10 分）如图，在ABC 中，ABAC，B30，D 为 BC 边上一点，DAB45 （1）求DAC 的度数； （2）请说明：ABCD 22 （
7、本题 10 分）在如图网格中画图： 画A1B1C1，使它与ABC 关于 l1对称； 画A2B2C2，使它与A1B1C1关于 l2对称； 画A3B3C3，使它与A2B2C2关于 l3对称； 画出A3B3C3与ABC 的对称轴 23 （本题 10 分）如图，在ABC 中，C90，AD 是BAC 的平分线，DEAB 于 E，F 在 AC 上，且 BDDF （1）求证：CFEB； （2）试判断 AB 与 AF，EB 之间存在的数量关系并说明理由 四校 2020 秋学期 八年级数学 第 1 次学情调查 试题 共 4 页 第 4 页 24 （本题 12 分）已知：如图，ABC 和CDE 都是等边三角形，且
8、点 A、C、E 在一条直线上，AD 与 BE 相交于点 P，AD 与 BC 相交于点 M，BE 与 CD 相交于点 N 求证： （1）APB60； （2）CMCN 25 （本题 12 分）如图，在ABC 中，ABAC，ADBC，CEAB，AECE （1）求证：AEFCEB （2）猜想：AF 与 CD 之间存在怎样的数量关系？请说明理由 26 （本题 14 分）如图，在ABC 中，ACB90，AC6，BC8点 P 从点 A 出发，沿折线 ACCB 以每秒 1 个单位长度的速度向终点 B 运动，点 Q 从点 B 出发沿折线 BCCA 以每秒 3 个单位长度的速度向 终点 A 运动， P、 Q 两点
9、同时出发分别过 P、Q 两点作 PEl 于 E，QFl 于 F设点 P 的运动时间为 t（秒） ： （1）当 P、Q 两点相遇时，求 t 的值； （2）在整个运动过程中，求 CP 的长（用含 t 的代数式表示） ； （3）当PEC 与QFC 全等时，直接写出所有满足条件的 CQ 的长 lFE A C B P Q 四校 2020 秋学期 八年级数学 第 1 次学情调查 试题 共 4 页 第 5 页 四校 20202021 学年度第一学期第 1 次学情调查 八年级数学试题 参考答案与试题解析 一选择题（共一选择题（共 6 小题）小题） 1A 2C 3C 4D 5B 6B 二填空题（共二填空题（共
10、10 小题）小题） 780 8AD 917 1012 113 1215 1355 147 154 161822.5 三解答题（共三解答题（共 10 小题）小题） 17解：如图，点 P 即为所求 (8(8 分）分） 18证明：12， 1EAC2EAC， 即BACEAD， 在ABC 和AED 中， DC BACEAD ABAE ， ABCAED（AAS） (8(8 分）分） 19证明：BECF（已知） ， BEECECCF， 即 BCEF， 在ABC 和DEF 中， AD BDEF BCEF ABCDEF（AAS） ， ACDF（全等三角形对应边相等） (8(8 分）分） 20证明：如图，连接 B
11、M、DM， ABCADC90，M 是 AC 的中点， 四校 2020 秋学期 八年级数学 第 1 次学情调查 试题 共 4 页 第 6 页 BMDM 1 2 AC， 点 N 是 BD 的中点， MNBD (10(10 分）分） 21 （1）解： ABAC， BC30， CBACB180， BAC1803030120， DAB45， DACBACDAB1204575；(5(5 分）分） （2）证明：DAB45， ADCBDAB75， DACADC， DCAC， ABAC， ABCD(10(10 分）分） 22解：如图，A1B1C1、A2B2C2、A3B3C3、直线 l 即为所求； (10(10
12、分）分） 23 （1）证明：AD 是BAC 的平分线，DEAB，C90， DCDE， 在 RtFCD 和 RtBED 中， DCDE DFDB ， RtFCDRtBED（HL） ， CFEB；(5(5 分）分） （2）解：在 RtACD 和 RtAED 中， DCDE ADAD ， RtACDRtAED（HL） ， ACAE， ABAEBEAFFCBEAF2BE(10(10 分）分） 24证明： （1）ABC 和CDE 都是等边三角形， ACBC，DCEC，ACBDCE60， ACBBCDDCEBCD， 即ACDBCE， 在ACD 和BCE 中， ACBC ACDBCE DCEC ACDBCE
13、（SAS） ， CADCBE 四校 2020 秋学期 八年级数学 第 1 次学情调查 试题 共 4 页 第 7 页 又AMCBMP， APBACB60；(6(6 分）分） （2）在ACM 和BCN 中， CADCBE ACBC ACBBCD ACMBCN（ASA） ， CMCN(12(12 分）分） 25 （1）证明：ADBC，CEAB， AEFBECADB90， EAFBBBCE90， 即EAFBCE 在AEF 和CEB 中， EAFBCE AECE AEFCEB ， AEFCEB（ASA） (6(6 分）分） （2）解：AF2CD 理由：由（1）得 AFBC ABAC，ADBC， BC2C
14、D， AF2CD(12(12 分）分） 26解： （1）由题意得 t3t68，解得 t 7 2 （秒） ，当 P、Q 两点相遇时，t 的值为 7 2 秒；(4(4 分）分） （2）由题意可知 APt， 则 CP 的长为 6(6) 6(614) t t tt ；(8(8 分）分） （3）当 P 在 AC 上，Q 在 BC 上时， ACB90， PCEQCF90， PEl 于 E，QFl 于 F EPCPCE90，PECCFQ90， EPCQCF， PCECQF， PCCQ， 6t83t，解得 t1， CQ83t5； 当 P 在 AC 上，Q 在 AC 上时，即 P、Q 重合时，则 CQPC， 由题意得，6t3t8， 解得 t3.5， CQ3t82.5， 当 P 在 BC 上，Q 在 AC 上时，即 A、Q 重合时，则 CQAC6， 综上，当PEC 与QFC 全等时，满足条件的 CQ 的长为 5 或 2.5 或 6(14(14 分）分）
