1、第第 3 章章 统计案例统计案例 章末复习章末复习 学习目标 1.理解独立性检验的基本思想及实施步骤.2.会求线性回归方程，并用回归直线进 行预测 122 列联表 22 列联表如表所示： B B 合计 A a b ab A c d cd 合计 ac bd n 其中 nabcd 为样本容量 2最小二乘法 对于一组数据(xi，yi)，i1,2，n，如果它们线性相关，则线性回归方程为y b xa ，其 中b i1 n xi x yi y i1 n xi x 2 i1 n xiyin x y i1 n x2in x 2 ，a y b x . 3独立性检验 常用统计量 2 nadbc2 abcdacbd
2、来检验两个变量是否有相关关系. 类型一 独立性检验 例 1 为了解某班学生喜爱打篮球是否与性别有关， 对本班 48 人进行了问卷调查得到了如下 的 22 列联表： 喜爱打篮球 不喜爱打篮球 合计 男生 6 女生 10 合计 48 已知在全班 48 人中随机抽取 1 人，抽到喜爱打篮球的学生的概率为2 3. (1)请将上面的 22 列联表补充完整；(不用写计算过程) (2)能否在犯错误的概率不超过 0.05 的前提下认为喜爱打篮球与性别有关？说明你的理由； (3)现从女生中抽取 2 人进一步调查，设其中喜爱打篮球的女生人数为 X，求 X 的概率分布与 均值 考点 独立性检验及其基本思想 题点 独
3、立性与均值的综合应用 解 (1)列联表补充如下： 喜爱打篮球 不喜爱打篮球 合计 男生 22 6 28 女生 10 10 20 合计 32 16 48 (2)由 2 48220602 282032164.286. 因为 4.2863.841， 所以能在犯错误的概率不超过 0.05 的前提下认为喜爱打篮球与性别有关 (3)喜爱打篮球的女生人数 X 的可能取值为 0,1,2，其概率分别为 P(X0)C 2 10 C220 9 38， P(X1)C 1 10C 1 10 C220 10 19， P(X2)C 2 10 C220 9 38， 故 X 的概率分布为 X 0 1 2 P 9 38 10 1
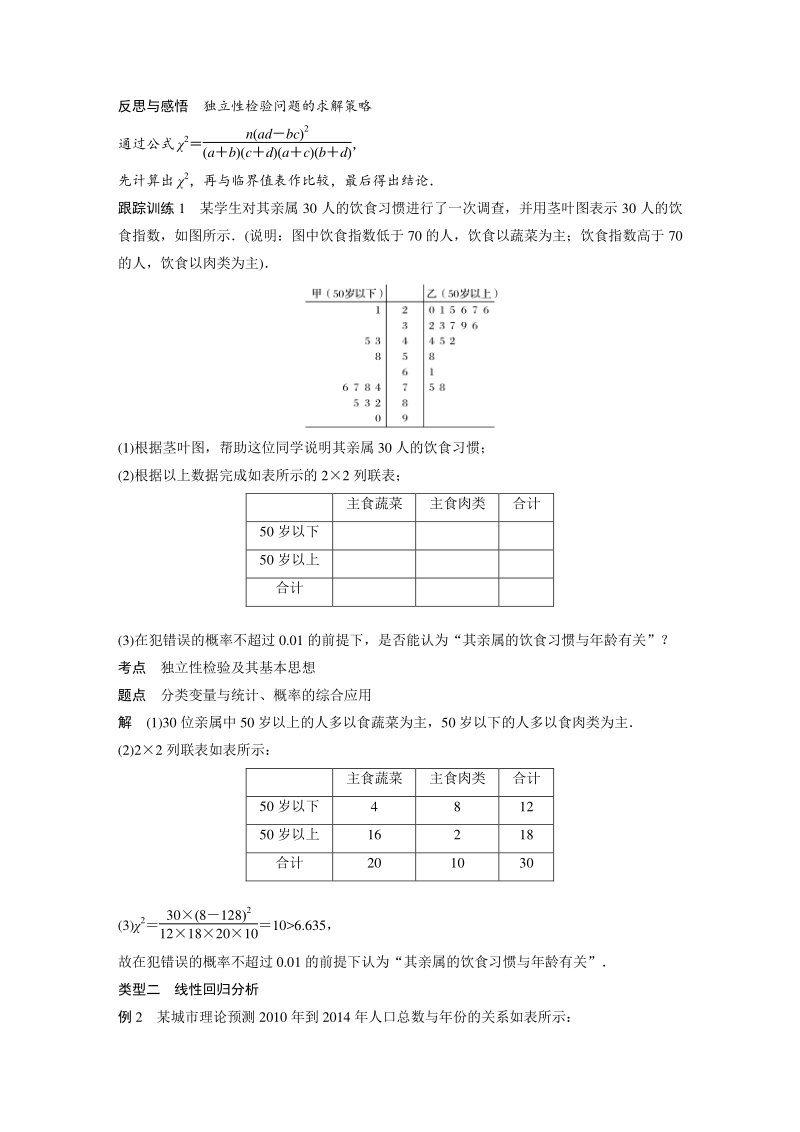
4、9 9 38 X 的均值 E(X)010 19 9 191. 反思与感悟 独立性检验问题的求解策略 通过公式 2 nadbc2 abcdacbd， 先计算出 2，再与临界值表作比较，最后得出结论 跟踪训练 1 某学生对其亲属 30 人的饮食习惯进行了一次调查，并用茎叶图表示 30 人的饮 食指数，如图所示(说明：图中饮食指数低于 70 的人，饮食以蔬菜为主；饮食指数高于 70 的人，饮食以肉类为主) (1)根据茎叶图，帮助这位同学说明其亲属 30 人的饮食习惯； (2)根据以上数据完成如表所示的 22 列联表； 主食蔬菜 主食肉类 合计 50 岁以下 50 岁以上 合计 (3)在犯错误的概率不
5、超过 0.01 的前提下，是否能认为“其亲属的饮食习惯与年龄有关”？ 考点 独立性检验及其基本思想 题点 分类变量与统计、概率的综合应用 解 (1)30 位亲属中 50 岁以上的人多以食蔬菜为主，50 岁以下的人多以食肉类为主 (2)22 列联表如表所示： 主食蔬菜 主食肉类 合计 50 岁以下 4 8 12 50 岁以上 16 2 18 合计 20 10 30 (3)2 3081282 12182010106.635， 故在犯错误的概率不超过 0.01 的前提下认为“其亲属的饮食习惯与年龄有关” 类型二 线性回归分析 例 2 某城市理论预测 2010 年到 2014 年人口总数与年份的关系如
6、表所示： 年份 201x(年) 0 1 2 3 4 人口数 y(十万) 5 7 8 11 19 (1)请画出上表数据的散点图； (2)请根据上表提供的数据，求出 y 关于 x 的线性回归方程y b xa ； (3)据此估计 2019 年该城市人口总数 考点 回归分析思想的应用 题点 回归分析思想的应用 解 (1)散点图如图： (2)因为 x 01234 5 2， y 5781119 5 10， i1 5 xiyi051728311419132， i1 5 x2i021222324230， 所以b 1325210 30522 3.2， a y b x 3.6. 所以线性回归方程为y 3.2x3.
7、6. (3)令 x9，则y 3.293.632.4， 故估计 2019 年该城市人口总数为 32.4(十万) 反思与感悟 解决回归分析问题的一般步骤 (1)画散点图：根据已知数据画出散点图 (2)判断变量的相关性并求回归方程： 通过观察散点图， 直观感知两个变量是否具有相关关系； 在此基础上，利用最小二乘法求回归系数，然后写出回归方程 (3)实际应用：依据求得的回归方程解决实际问题 跟踪训练 2 在一段时间内，某种商品的价格 x(元)和需求量 y(件)之间的一组数据为： x(元) 14 16 18 20 22 y(件) 12 10 7 5 3 且知 x 与 y 具有线性相关关系，求出 y 关于
8、 x 的线性回归方程 考点 回归分析思想的应用 题点 回归分析思想的应用 解 x 1 5(1416182022)18， y 1 5(1210753)7.4， i1 5 x2i1421621822022221 660， i1 5 xiyi14121610187205223620， 所以b i1 5 xiyi5 x y i1 5 x2i5 x 2 6205187.4 1 6605182 1.15， 所以a 7.41.151828.1， 所以 y 对 x 的线性回归方程为y 1.15x28.1. 1下面是一个 22 列联表： y1 y2 合计 x1 a 21 70 x2 5 c 30 合计 b d
9、100 则 bd_. 考点 题点 答案 8 解析 a702149，c30525， b49554，d212546， bd8. 2 “回归”一词是在研究子女的身高与父母的身高之间的遗传关系时由高尔顿提出的， 他的 研究结果是子代的平均身高向中心回归根据他的结论，在儿子的身高 y 与父亲的身高 x 的 线性回归方程y b xa 中，b 的取值范围是_ 考点 线性回归分析 题点 线性回归方程的应用 答案 (0,1) 解析 子代平均身高向中心回归，b 应为正的真分数 3假如由数据：(1,2)，(3,4)，(2,2)，(4,4)，(5,6)，(3,3.6)可以得出线性回归方程y a b x， 则经过的定点
10、是以上点中的_ 考点 题点 答案 (3,3.6) 解析 易知，线性回归方程y a b x 经过定点( x ， y )，根据计算可知这几个点中满足条件 的是(3,3.6) 4考古学家通过始祖鸟化石标本发现：其股骨长度 x(cm)与肱骨长度 y(cm)的线性回归方程 为y 1.197x3.660，由此估计，当股骨长度为 50 cm 时，肱骨长度的估计值为_cm. 考点 题点 答案 56.19 解析 根据线性回归方程y 1.197x3.660，将 x50 代入，得 y56.19，则肱骨长度的估计 值为 56.19 cm. 5对于线性回归方程y b xa ，当 x3 时，对应的 y 的估计值是 17，
11、当 x8 时，对应的 y 的估计值是 22，那么，该线性回归方程是_，根据线性回归方程判断当 x_ 时，y 的估计值是 38. 考点 线性回归分析 题点 线性回归方程的应用 答案 y x14 24 解析 首先把两组值代入线性回归方程，得 217, 1, 14, 222, ba b a ba 解得 所以线性回归方程是y x14. 令 x1438，可得 x24，即当 x24 时，y 的估计值是 38. 1 独立性检验是对两个分类变量间是否存在相关关系的一种案例分析方法 利用假设的思想 方法，计算出某一个 2统计量的值来判断更精确些 2建立回归模型的基本步骤 (1)确定研究对象，明确哪个变量是自变量，哪个变量是因变量； (2)画出散点图，观察它们之间的关系； (3)由经验确定回归方程的类型； (4)按照一定的规则估计回归方程中的参数.
