1、第十二章第十二章 全等三角形单元检测 【基础篇基础篇】 一一. .选择题选择题 1. 如图所示，若ABEACF，且 AB5，AE2，则 EC 的长为（ ） A. .2 B. .3 C. .5 D. .2.5 2. 在ABC 中，BC，与ABC 全等的三角形有一个角是 100，那么在ABC 中与这 100角对应相等的角是（ ） A. A B. B C. C D. B 或C 3. 如图，ABCAEF，若ABC 和AEF 是对应角，则EAC 等于 （ ） AACB BCAF CBAF DBAC 4. 在下列结论中, 正确的是( ) A.全等三角形的高相等 B.顶角相等的两个等腰三角形全等 C. 一角
2、对应相等的两个直角三角形全等 D.一边对应相等的两个等边三角形全等 5. 如图，点 C、D 分别在AOB 的边 OA、OB 上，若在线段 CD 上求一点 P，使它到 OA，OB 的距离相等，则 P 点是（ ） A. 线段 CD 的中点 B. OA 与 OB 的中垂线的交点 C. OA 与 CD 的中垂线的交点 D. CD 与AOB 的平分线的交点 6在ABC 与DEF 中，给出下列四组条件： （1）ABDE，BCEF，ACDF； （2）ABDE， BE， BCEF； （3） BE， BCEF， CF；（4） ABDE， ACDF， BE 其 中，能使ABCDEF 的条件共有（ ）组 A1 组
3、B2 组 C3 组 D4 组 7. 如果两个锐角三角形有两条边和其中一边上的高对应相等，那么这两个三角形的第三条 边所对的角的关系是（ ） A. 相等 B.不相等 C.互补 D.相等或互补 8. ABC 中，BAC90 ADBC，AE 平分BAC，B2C，DAE 的度数是( ) A.45 B.20 C.、30 D.15 二二. .填空题填空题 9. 已知ABCA B C， 若ABC 的面积为 10 2 cm， 则 ABC的面积为_ 2 cm，若A B C的周长为 16cm，则ABC 的周长为_cm 10. ABC 和ADC 中，下列三个论断：ABAD；BACDAC；BCDC将两个论 断作为条件
4、，另一个论断作为结论构成一个命题，写出一个真命题：_ 11. 如图，直线 AEBD，点 C 在 BD 上，若 AE4，BD8，ABD 的面积为 16，则的 面积为_ 12. 下列说法中： 如果两个三角形可以依据 “AAS” 来判定全等， 那么一定也可以依据 “ASA” 来判定它们全等； 如果两个三角形都和第三个三角形不全等， 那么这两个三角形也一 定不全等；要判断两个三角形全等，给出的条件中至少要有一对边对应相等正确的 是_. 13. 如右图，在ABC 中，C90，BD 平分CBA 交 AC 于点 D若 ABa，CDb，则 ADB 的面积为_ 14如图，已知 ABBD, ABED，ABED，要
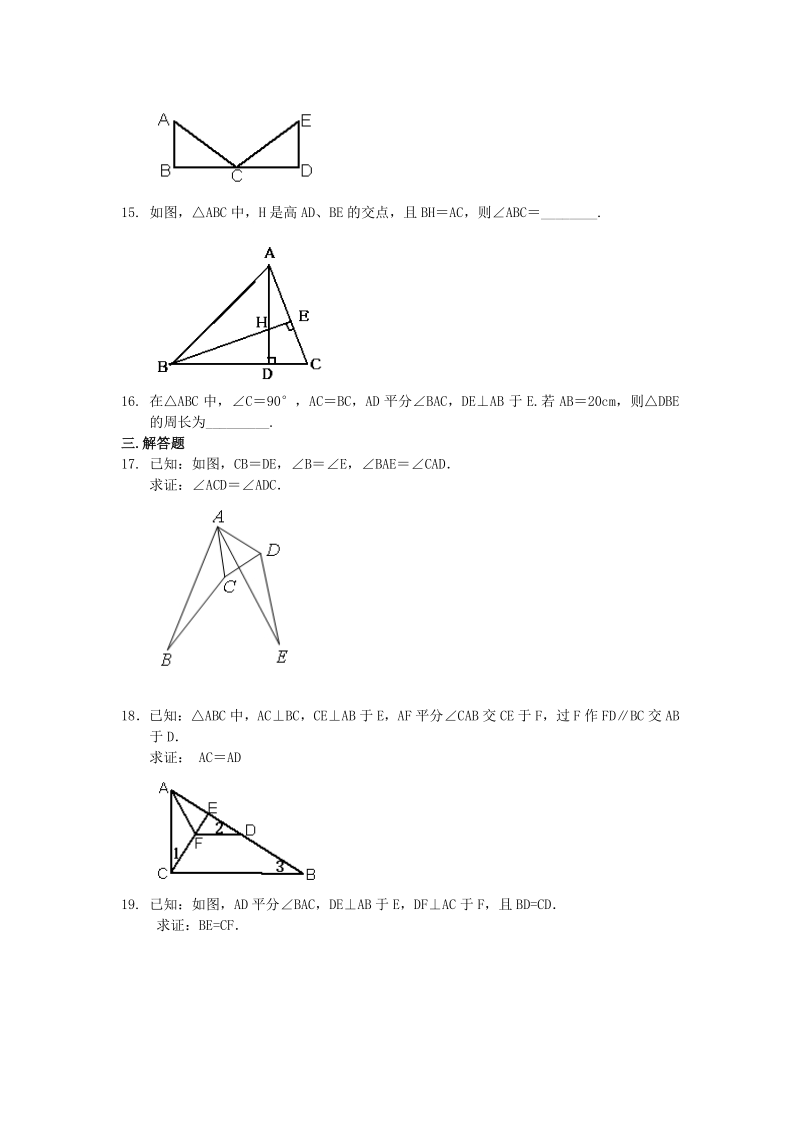
5、说明 ABCEDC，若以“SAS”为依据，还 要添加的条件为_； 若添加条件 ACEC， 则可以用_公理 （或定理） 判定全等. 15. 如图，ABC 中，H 是高 AD、BE 的交点，且 BHAC，则ABC_. 16. 在ABC 中，C90，ACBC，AD 平分BAC，DEAB 于 E.若 AB20cm，则DBE 的周长为_. 三三. .解答题解答题 17. 已知：如图，CBDE，BE，BAECAD 求证：ACDADC 18已知：ABC 中，ACBC，CEAB 于 E，AF 平分CAB 交 CE 于 F，过 F 作 FDBC 交 AB 于 D 求证： ACAD 19. 已知：如图，AD 平分
6、BAC，DEAB 于 E，DFAC 于 F，且 BD=CD 求证：BE=CF 20. 已知如图所示，PAPB，12180，求证：OP 平分AOB 【提高篇提高篇】 一一. .选择题选择题 1. 下列命题中, 错误的命题是( ) A.两边和其中一边上的中线对应相等的两个三角形全等 B.两边和第三边上的高对应相等的两个三角形全等 C.两边和第三边上的中线对应相等的两个三角形全等 D.两边和其夹角对应相等的两个三角形全等 2. 如图, 在AOB 的两边上截取 AO BO, CO DO, 连结 AD、BC 交于点 P. 则下列结论 正确的是( ) AODBOC； APCBPD； 点 P 在AOB 的平
7、分线上 A. 只有 B. 只有 C. 只有 D. 3. 如图, ABCD, ACBD, AD 与 BC 交于 O, AEBC 于 E, DFBC 于 F, 那么图中全等的三 角形有( ) A. 5 对 B. 6 对 C. 7 对 D. 8 对 4如图，ABBC 于 B，BEAC 于 E，12，D 为 AC 上一点，ADAB，则（ ） A1EFD B FDBC CBFDFCD DBEEC 5. 如图，ABCFDE，C40，F110，则B 等于（ ） A.20 B.30 C.40 D.150 6. 根据下列条件能画出唯一确定的ABC 的是（ ） A.AB3，BC4，AC8 B.AB4，BC3，A3
8、0 C.A60，B45，AB4 D.C90，ABAC6 7. 如图，已知 ABAC，PBPC，且点 A、P、D、E 在同一条直线上.下面的结论：EBEC； ADBC；EA 平分BEC；PBCPCB.其中正确的有（ ） A.1 个 B. 2 个 C.3 个 D. 4 个 8. 如图，AEAB 且 AE=AB，BCCD 且 BC=CD，请按照图中所标注的数据，计算图中实线所 围成的图形的面积 S 是（ ） A50 B62 C65 D68 二二. .填空题填空题 9. 在平面直角坐标系中，已知点 A（1，2） ，B（5，5） ，C（5，2） ，存在点 E，使ACE 和 ACB 全等，写出所有满足条件
9、的 E 点的坐标 10. 如图，ABC 中，H 是高 AD、BE 的交点，且 BHAC，则ABC_. 11. 在ABC 中，C90，ACBC，AD 平分BAC，DEAB 于 E.若 AB20cm，则DBE 的周长为_. 12. 如图，ABC 中，C90，EDAB，12，若 CD1.3cm，则点 D 到 AB 边的 距离是_. 13. 如图， RtABC 中， B90， 若点 O 到三角形三边的距离相等， 则AOC_. 14. 如图，BAAC，CDAB，BCDE，且 BCDE.若 AB2，CD6，则 AE_. 15. ABC 中，C90，BC40，AD 是BAC 平分线，交 BC 于点 D，且
10、DC：DB3:5， 则点 D 到 BA 的距离是_. 16. 如图，在ABC 中，ABAC，BAC90，AE 是过 A 点的一条直线，AECE 于 E，BD AE 于 D，DE4cm，CE2cm，则 BD_. 三三. .解答题解答题 17如图所示，已知在ABC 中，B60，ABC 的角平分线 AD、CE 相交于点 O， 求证：AECDAC 18. 在四边形 ABCP 中，BP 平分ABC，PDBC 于 D，且 ABBC2BD. 求证：BAPBCP180. 19. 如图：已知 AD 为ABC 的中线，且12，34,求证：BECFEF. 20已知：ABC 中，AD 平分BAC 交 BC 于点 D，
11、且ADC60 问题问题 1 1：如图 1，若ACB90，ACmAB，BDnDC， 则m的值为_，n的值为_ 问题问题 2 2：如图 2，若ACB 为钝角，且 ABAC，BDDC （1）求证：BDDCABAC； （2）若点 E 在 AD 上，且 DEDB，延长 CE 交 AB 于点 F，求BFC 的度数 【基础篇基础篇答案与解析】答案与解析】 一一. .选择题选择题 1. 【答案】B； 【解析】根据全等三角形对应边相等，ECACAE523； 2. 【答案】A； 【解析】如果选 B 或者 C 的话，三角形内角和就会超过 180. 3. 【答案】C； 【解析】EAFBAC，EACEAFCAFBACC
12、AFBAF. 4. 【答案】D； 【解析】A 项应为全等三角形对应边上的高相等；B 项如果腰不相等不能证明全等；C 项 直角三角形至少要有一边相等. 5. 【答案】D； 【解析】角平分线上的点到角两边的距离相等. 6. 【答案】C； 【解析】 （1） （2） （3）能使两个三角形全等. 7. 【答案】A； 【解析】高线可以看成为直角三角形的一条直角边，进而用 HL 定理判定全等. 8. 【答案】D； 【解析】由题意可得BDAC60，C30，所以DAE604515. 二二. .填空题填空题 9. 【答案】10，16； 【解析】全等三角形面积相等，周长相等. 10 【答案】； 11.【答案】8；
13、【解析】 1 16 2 BD h ，h4， 1 48 2 AE. 12.【答案】 【解析】不正确是因为存在两个全等的三角形与某一个三角形不全等的情况. 13.【答案】ab 2 1 ； 【解析】由角平分线的性质，D 点到 AB 的距离等于 CDb，所以ADB 的面积为ab 2 1 . 14.【答案】BCDC ，HL； 15.【答案】45； 【解析】RtBDHRtADC，BDAD. 16.【答案】20cm； 【解析】BCACAE，DBE 的周长等于 AB. 三三. .解答题解答题 17 【解析】 证明：BAECAD， BAECAE CADCAE， 即BACEAD 在ABC 和AED 中， BACE
14、AD BE BCED ， ， ， ABCAED （AAS） ACAD ACDADC 18.【解析】 证明：ACBC，CEAB CAB1CAB390， 13 又FDBC 23， 12 在CAF 与DAF 中 CAF= DAF 1= 2 AF=AF CAF 与DAF（AAS） ACAD. 19.【解析】 证明：AD 平分BAC，DEAB 于 E，DFAC 于 F， （已知） DE=DF（角平分线上的点到角两边距离相等） 又BD=CD BDECDF（HL） BE=CF 20.【解析】 证明：如图所示，过点 P 作 PEAO，PFOB， 垂足分别为 E、F 21180， 又2PBO180， 1PBO
15、在AEP 和BFP 中， AEPBFP（AAS） PEPF（全等三角形对应边相等） OP 平分AOB（到角两边距离相等的点在这个角的平分线上） 【提高篇提高篇答案与解析】答案与解析】 一一. .选择题选择题 1. 【答案】B； 【解析】B 项如果这两个三角形一个是锐角三角形，一个是钝角三角形，则虽然有两边 和第三边上的高对应相等，但是不全等. 2. 【答案】D； 【解析】可由 SAS 证，由和 AAS 证，SSS 证. 3. 【答案】C； 4. 【答案】B ； 【解析】证ADFABF，则ABFADFACB，所以 FDBC. 5. 【答案】B； 【解析】CE，BFDE1801104030. 6.
16、 【答案】C； 【解析】A 项构不成三角形，B 项是 SSA，D 项斜边和直角边一样长，是不可能的. 7. 【答案】D； 8. 【答案】A； 【解析】易证EFAABG 得 AF=BG，AG=EF同理证得BGCDHC 得 GC=DH， CH=BG故 FH=FA+AG+GC+CH=3+6+4+3=16，故 S= 1 2 （6+4）16-34-63=50 二二. .填空题填空题 9. 【答案】 （1，5）或（1，1）或（5，1） ； 10.【答案】45； 【解析】RtBDHRtADC，BDAD. 11.【答案】20cm； 【解析】BCACAE，DBE 的周长等于 AB. 12.【答案】1.3cm；
17、【解析】AD 是BAC 的平分线，点 D 到 AB 的距离等于 DC. 13.【答案】135； 【解析】点 O 为角平分线的交点，AOC180 1 2 （BACBCA）135. 14.【答案】4； 【解析】证ABCCED. 15.【答案】15； 【解析】作 DEAB 于 E，则 DECD. 16.【答案】6cm； 【解析】CAEABD，ABDCAE. 三三. .解答题解答题 17.【解析】 证明：如图所示，在 AC 上取点 F，使 AFAE，连接 OF， 在AEO 和AFO 中， , 12 , AEAF AOAO AEOAFO（SAS） EOAFOA B60， AOC180(OACOCA) 1
18、80 1 2 (BACBCA) 180 1 2 (18060) 120 AOEAOFCOFDOC60 在COD 和COF 中， , , , CODCOF OCOC OCDOCF CODCOF（ASA） CDCF AECDAFCFAC 18.【解析】 证明：过点 P 作 PEAB，交 BA 的延长线于 E， BP 平分ABC，PDBC ，PEAB， PEPD 在 RtPBE 与 RtPBD 中，BPBP，PEPD RtPBERtPBD（HL） BEBD 又ABBC2BD. ABBDDC2BD，即 ABDCBD AEDC 由（SAS）可证 RtPEARtPDC， PAEPCD BAPPAE180
19、BAPBCP180. 19.【解析】 证明：在 DA 上截取 DNDB，连接 NE，NF，则 DNDC， 在DBE 和DNE 中： DBEDNE （SAS） BENE（全等三角形对应边相等） 同理可得：CFNF 在EFN 中 ENFNEF（三角形两边之和大于第三边） BECFEF. 20 【解析】 证明：问题问题 1 1： 2 1 ，2 ； 问题问题 2 2： （1）在 AB 上截取 AG，使 AGAC，连接 GD （如图） AD 平分BAC， 12 在AGD 和ACD 中， AGAC 12 ADAD AGDACD DGDC BGD 中，BDDGBG， BDDCBG BG ABAG ABAC， BDDCABAC （2）由（1）知AGDACD， GDCD，4 360 5 18034180606060 5 3 在BGD 和ECD 中， 53 DBDE DGDC ， BGDECD B 6 BFC 中，BFC180B7 18067 3， BFC60
