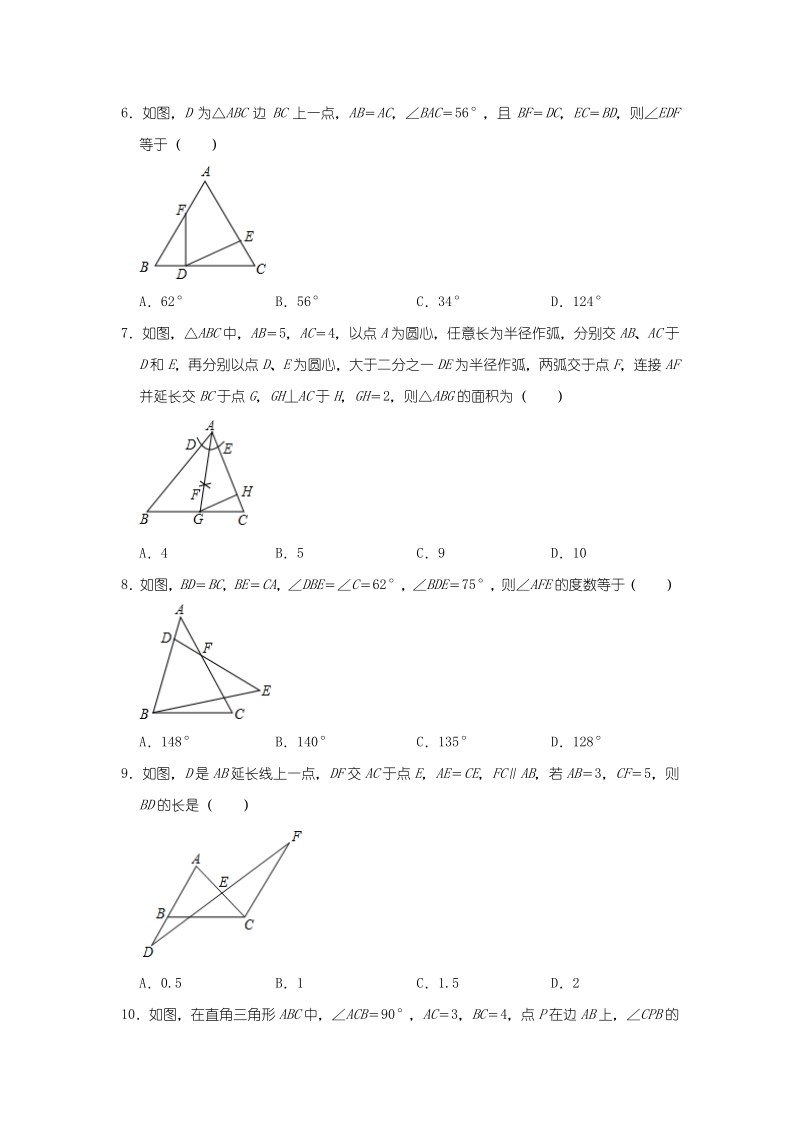
1、课时练：第十二章课时练：第十二章 全等三角形全等三角形 （提升篇）（提升篇） 时间：时间：100100 分钟分钟 满分：满分：100100 分分 一选择题（每小题一选择题（每小题 3 3 分，共分，共 3030 分）分） 1下列所给的四组条件，能作出唯一三角形的是（ ） AAB4cm，BC3cm，AC5cm BAB2cm，BC6cm，AC4cm CABC60 DA30，B60，C90 2如图，在ABC中，C90，DEAB于点E，CDDE，CBD26，则A的度数为 （ ） A40 B34 C36 D38 3如图，已知ACAD，ACBADB90，则全等三角形共有（ ） A1 对 B2 对 C3 对
2、 D4 对 4下列说法不正确的是（ ） A面积相等的两个三角形全等 B全等三角形对应边上的中线相等 C全等三角形的对应角的角平分线相等 D全等三角形的对应边上的高相等 5如图，ABCABC，BCB30，则ACA的度数为（ ） A30 B45 C60 D15 6如图，D为ABC边BC上一点，ABAC，BAC56，且BFDC，ECBD，则EDF 等于（ ） A62 B56 C34 D124 7如图，ABC中，AB5，AC4，以点A为圆心，任意长为半径作弧，分别交AB、AC于 D和E，再分别以点D、E为圆心，大于二分之一DE为半径作弧，两弧交于点F，连接AF 并延长交BC于点G，GHAC于H，GH2
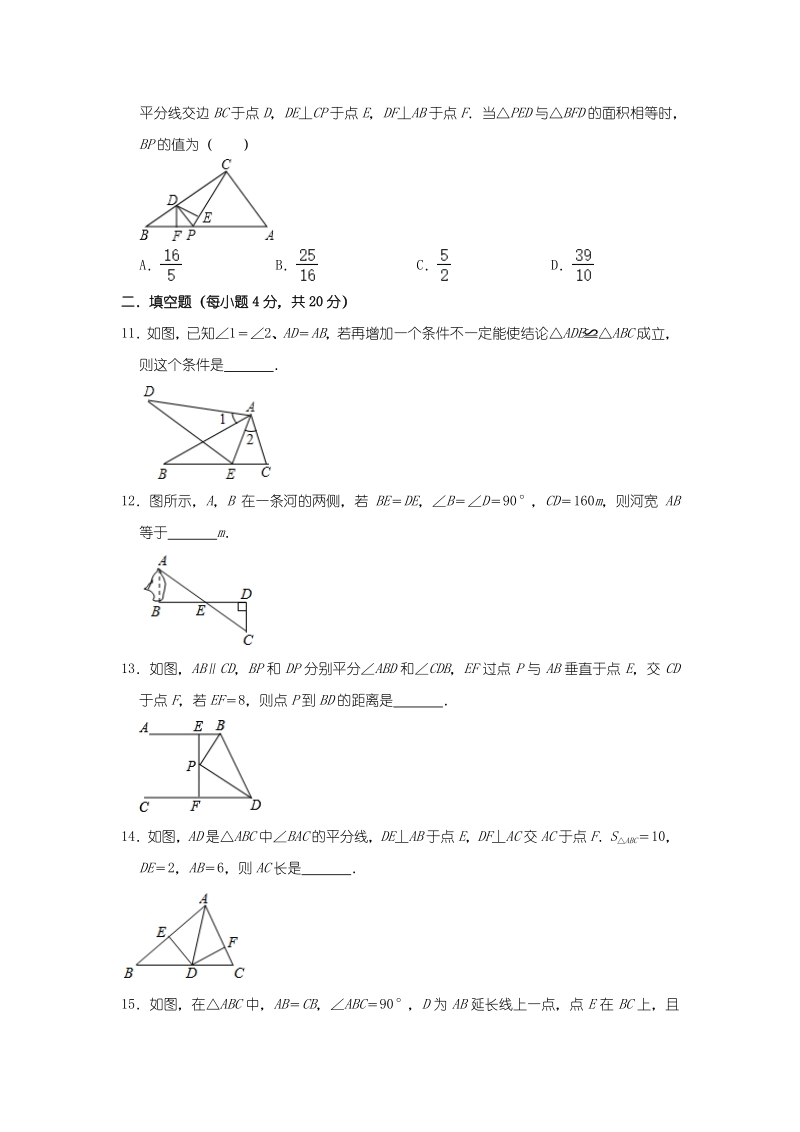
3、，则ABG的面积为（ ） A4 B5 C9 D10 8如图，BDBC，BECA，DBEC62，BDE75，则AFE的度数等于（ ） A148 B140 C135 D128 9如图，D是AB延长线上一点，DF交AC于点E，AECE，FCAB，若AB3，CF5，则 BD的长是（ ） A0.5 B1 C1.5 D2 10如图，在直角三角形ABC中，ACB90，AC3，BC4，点P在边AB上，CPB的 平分线交边BC于点D，DECP于点E，DFAB于点F当PED与BFD的面积相等时， BP的值为（ ） A B C D 二填空题二填空题（每小题（每小题 4 4 分，共分，共 2020 分）分） 11如图
4、，已知12、ADAB，若再增加一个条件不一定能使结论ADEABC成立， 则这个条件是 12图所示，A，B在一条河的两侧，若BEDE，BD90，CD160m，则河宽AB 等于 m 13如图，ABCD，BP和DP分别平分ABD和CDB，EF过点P与AB垂直于点E，交CD 于点F，若EF8，则点P到BD的距离是 14如图，AD是ABC中BAC的平分线，DEAB于点E，DFAC交AC于点FSABC10， DE2，AB6，则AC长是 15如图，在ABC中，ABCB，ABC90，D为AB延长线上一点，点E在BC上，且 BEBD，连接AE、DE、DC若CAE30，则BDC 三解答题三解答题（每题（每题 10
5、10 分，共分，共 5050 分）分） 16如图，四边形ABCD中，ADBC，DEEC，连接AE并延长交BC的延长线于点F，连接 BE （1）求证：AEEF； （2）若BEAF，求证：BCABAD 17如图，在ABC中，BD，CE分别是AC，AB边上的高，在BD上截取BFAC，延长CE至 点G使CGAB，连接AF，AG （1）如图 1，求证：AGAF； （2）如图 2，若BD恰好平分ABC，过点G作GHAC交CA的延长线于点H，请直接写 出图中所有的全等三角形并用全等符号连接 18如图，ABCD，AD与BC相交于点E，AF平分BAD，交BC于点F，交CD的延长线于点 G （1）若G29，求AD
6、C的度数； （2）若点F是BC的中点，求证：ABAD+CD 19如图，ADC中，DB是高，点E是DB上一点，ABDB，EBCB，M，N分别是AE，CD 上的点，且AMDN （1）求证：ABEDBC （2）探索BM和BN的关系，并证明你的结论 20已知，在ABC中，ACBC分别过A，B点作互相平行的直线AM和BN过点C的直线 分别交直线AM，BN于点D，E （1）如图 1若CDCE求ABE的大小； （2）如图 2ABCDEB60求证：AD+DCBE 参考答案参考答案 一选择题 1 A 2 D 3 C 4 A 5 A 6 A 7 B 8 A 9 D 10 D 二填空题 11 DEBC 12 160
7、 13 4 144 15 75 三解答题 16证明：（1）ADBC， DAEF，ADEFCE， 又DECE， ADEFCE（AAS）， AEEF； （2）AEEF，BEAF， ABBF， ADEFCE， ADCF， ABBC+CFBC+AD， BCABAD 17证明：（1）BD、CE分别是AC、AB两条边上的高， AECADB90， ABD+BADACE+CAE90， ABDACG， 在AGC与FAB中， AGCFAB（SAS）， AGAF； （2）图中全等三角形有AGCFAB，由得出CGHBAD， 由得出 RtAGHRtAFD，ABDCBD；CBDGCH 18证明：（1）ABCD， BAGG
8、，BADADC AF平分BAD， BAD2BAG2G ADCBAD2G G29， ADC58； （2）AF平分BAD， BAGDAG BAGG， DAGG ADGD 点F是BC的中点， BFCF 在ABF和GCF中， ABFGCF（AAS）， ABGC ABGD+CDAD+CD 19（1）证明：DB是高， ABEDBC90 在ABE和DBC中， ABEDBC （2）解：BMBN，MBBN 证明如下： ABEDBC， BAMBDN 在ABM 和DBN 中， ABMDBN（SAS） BMBN，ABMDBN DBN+DBMABM+DBMABD90 MBBN 20（1）解：如图 1，延长AC交BN于点
9、F， AMBN， DAFAFB， 在ADC和FEC中， ADCFEC（AAS）， ACFC， ACBC， BCACFCAF， ABF是直角三角形， ABE90； （2）证明：如图 2，在EB上截取EHEC，连CH， ACBC，ABC60， ABC为等边三角形， DEB60， CHE是等边三角形， CHE60，HCE60， BHC120， AMBN， ADC+BEC180， ADC120， DAC+DCA60， 又DCA+ACB+BCH+HCE180， DCA+BCH60， DACBCH， 在DAC与HCB中， DACHCB（AAS）， ADCH，DCBH， 又CHCEHE， BEBH+HEDC+AD， 即AD+DCBE
