1、课时练：第十二章课时练：第十二章 全等三角形全等三角形 （基础篇）（基础篇） 时间：100 分钟 满分：100 分 一选择题（一选择题（每小题每小题 3 3 分，分，共共 3030 分分） 1下列说法正确的是（ ） A三个角对应相等的两个三角形全等 B两角对应相等，且一条边也对应相等的两个三角形全等 C两边和其中一边的对角对应相等的两个三角形全等 D有两个角与一边对应相等的两个三角形不一定全等 2如图点O在ABC内，且到三边的距离相等若A50，则BOC等于（ ） A115 B105 C125 D130 3如图，AC与DB交于点O，下列条件不能证明ABCDCB的是（ ） AABDC，ACDB B
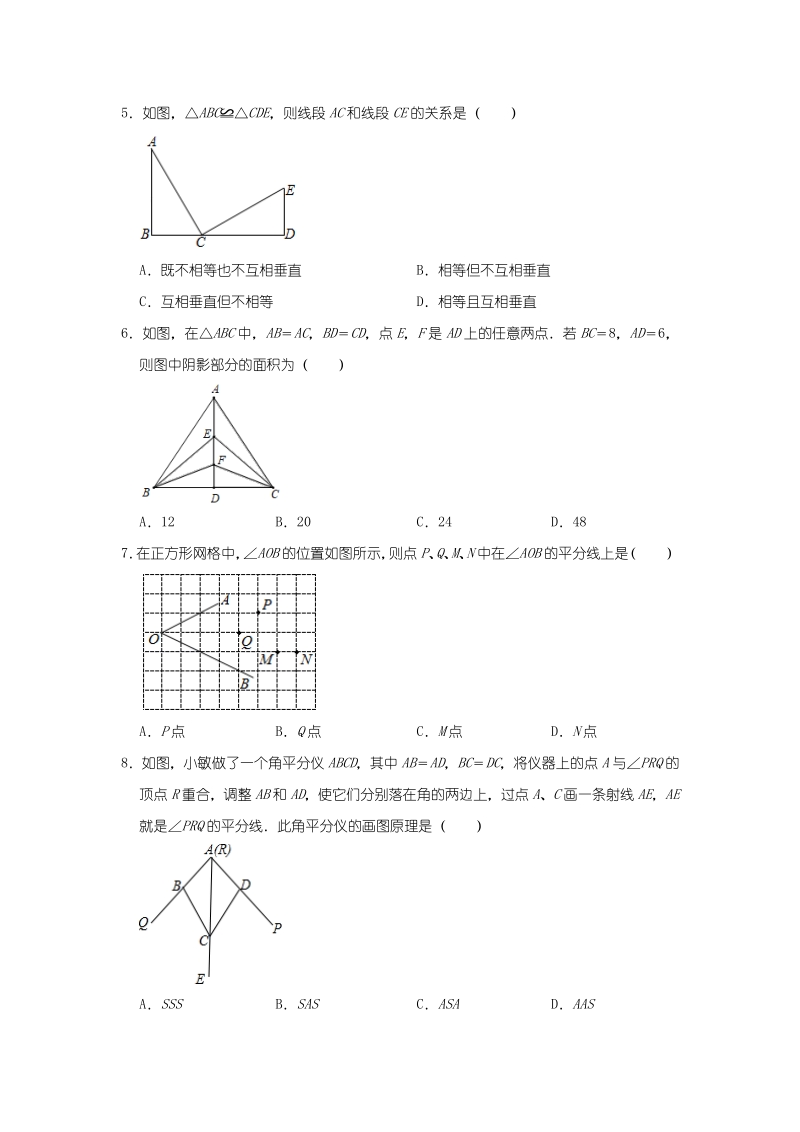
2、AD，ABCDCB CBOCO，AD DABDC，ACBDBC 4在如图所示的 66 网格中，ABC是格点三角形（即顶点恰好是网格线的交点），则与 ABC有一条公共边且全等（不含ABC）的所有格点三角形的个数是（ ） A3 个 B4 个 C6 个 D7 个 5如图，ABCCDE，则线段AC和线段CE的关系是（ ） A既不相等也不互相垂直 B相等但不互相垂直 C互相垂直但不相等 D相等且互相垂直 6如图，在ABC中，ABAC，BDCD，点E，F是AD上的任意两点若BC8，AD6， 则图中阴影部分的面积为（ ） A12 B20 C24 D48 7 在正方形网格中， AOB的位置如图所示， 则点P、
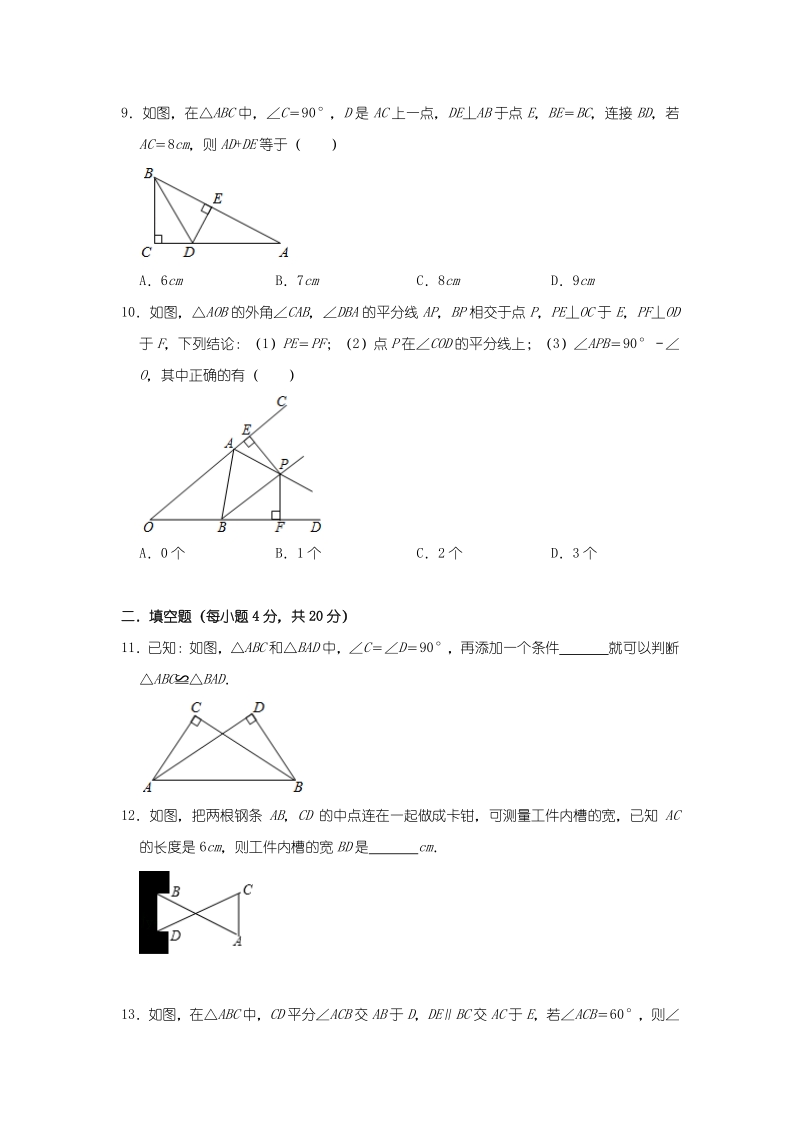
3、Q、M、N中在AOB的平分线上是 （ ） AP点 BQ点 CM点 DN点 8如图，小敏做了一个角平分仪ABCD，其中ABAD，BCDC，将仪器上的点A与PRQ的 顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A、C画一条射线AE，AE 就是PRQ的平分线此角平分仪的画图原理是（ ） ASSS BSAS CASA DAAS 9如图，在ABC中，C90，D是AC上一点，DEAB于点E，BEBC，连接BD，若 AC8cm，则AD+DE等于（ ） A6cm B7cm C8cm D9cm 10如图，AOB的外角CAB，DBA的平分线AP，BP相交于点P，PEOC于E，PFOD 于F，下列结论
4、：（1）PEPF；（2）点P在COD的平分线上；（3）APB90 O，其中正确的有（ ） A0 个 B1 个 C2 个 D3 个 二填空题二填空题（每小题（每小题 4 4 分，共分，共 2020 分）分） 11已知：如图，ABC和BAD中，CD90，再添加一个条件 就可以判断 ABCBAD 12如图，把两根钢条AB，CD的中点连在一起做成卡钳，可测量工件内槽的宽，已知AC 的长度是 6cm，则工件内槽的宽BD是 cm 13如图，在ABC中，CD平分ACB交AB于D，DEBC交AC于E，若ACB60，则 EDC 14如图，AD是ABC中BAC的平分线，DEAB于点E，DFAC交AC于点FSABC
5、10， DE2，AB6，则AC长是 15如图，EB交AC于点M，交C于点D，AB交FC于点N，EF90，BC，AE AF，给出下列结论：12；CDDN；ACNABM；BECF其中正确 的结论有 （填序号） 三解答题三解答题（每题（每题 1010 分，共分，共 5050 分）分） 16如图，在ABC和DBE中，点D在边AC上，BC与DE交于点P，ABDB，ABDE， ABDCBE （1）求证：BCBE； （2）若ADDC2.5，BC4，求CDP与BEP的周长之和 17如图，已知点B，E在线段CF上，CEBF，CF，ABCDEF 试说明：ABCDEF 解：因为CEBF（已知） 所以CE BFBE（
6、 ） 即 在ABC和DEF中 ， 所以ABCDEF（ ） 18如图，点B，E，C，F在一条直线上，ABDE，ACDF，BECF试说明： （1）ABCDEF； （2）AEGC 19如图，已知ABDC，ABCD，E、F是AC上两点，且AFCE （1）求证：ABECDF； （2）若BCE30，CBE70，求CFD的度数 20如图，在ABC中，ABAC8，BC12，点D从B出发以每秒 2 个单位的速度在线段 BC上从点B向点C运动，点E同时从C出发以每秒 2 个单位的速度在线段CA上向点A 运动，连接AD、DE，设D、E两点运动时间为t秒（0t4） （1）运动 秒时，AEDC； （2）运动多少秒时，A
7、BDDCE能成立，并说明理由； （3）若ABDDCE，BAC，则ADE （用含的式子表示） 参考答案 一选择题 1解：A、如图， ADE和ABC的三角对应相等，但两三角形不全等，错误，故本选项不符合题意； B、两角对应相等，且一条边也对应相等的两个三角形全等，符合全等三角形的判定定理 ASA或AAS，正确，故本选项符合题意； C、如图， ACAD，ABAB，BB，但是ABD和ABC不全等，错误，故本选项不符合题意； D、如图， ABC和DEF中，BE90，AF，BCEF， 当ABC和DEF不全等，错误，故本选项不符合题意； 故选：B 2解：点O在ABC内，且到三边的距离相等， 点O为ABC的内
8、角平分线的交点， 即OB平分ABC，OC平分ACB， OBCABC，OCBACB， BOC180ABCACB180（ABC+ACB）， 而ABC+ACB180A， BOC180（180A） 90+A 90+50 115 故选：A 3解：A在ABC和DCB中， ， ABCDCB（SSS），故A选项不合题意； B在ABC和DCB中， ， ABCDCB（AAS），故B选项不合题意； CBOCO， ACBDBC， 在ABC和DCB中， ， ABCDCB（AAS），故C选项不合题意； DABDC，ACBDBC，不能证明ABCDCB，故D选项符合题意； 故选：D 4解：如图所示：一共有 6 个符合题意的点
9、 故选：C 5解：ABCCDE， ACCE，ABCD，BD，ACBE， ACB+BCDACB+A， 当BD90时，ACB+BCDACB+A90， 则ACE90， 即AC和CE不互相垂直， 故选：B 6解：ABAC，BDCD，ADAD， ADCADB（SSS）， SADCSADB，BDBC， BC8， BD4， SBEFSCEF，AD6， S阴影SADB 故选：A 7解：如图，C点到OA、OB的距离相等， 所以OC平分AOB， 所以Q在AOB的平分线 故选：B 8解：在ABC和ADC中， ， ABCADC（SSS）， BACDAC， AE就是PRQ的平分线， 故选：A 9解：DEAB， DEB9
10、0， 在 RtBCD和 RtBED中， ， RtBCDRtBED（HL）， CDDE， AD+DEAD+CDAC， AC8cm， AD+DEAC8cm 故选：C 10解：（1）证明：作PHAB于H， AP是CAB的平分线， PAEPAH， 在PEA和PHA中， ， PEAPHA（AAS）， PEPH， 同理，PFPH， PEPF， （1）正确； （2）与（1）可知：PEPF， 又PEOC于E，PFOD于F， 点P在COD的平分线上， （2）正确； （3）O+OEP+EPF+OFP360， 又OEP+OFP90+90180， O+EPF180， 即O+EPA+HPA+HPB+FPB180， 由（
11、1）知：PEAPHA， EPAHPA， 同理：FPBHPB， O+2（HPA+HPB）180， 即O+2APB180， APB90， （3）错误； 故选：C 二填空题（共 5 小题） 11解：添加ACBD， 理由：CD90， ACB和BDA都是直角三角形， 在 RtABC和 RtBAD中， RtABCRtBAD（HL）， 故答案为：ACBD 12解：把两根钢条AB，CD的中点连在一起做成卡钳， AOBO，CODO， 在BOD和AOC中， BODAOC（SAS）， BDAC6cm， 故答案为：6 13解：如图，在ABC中，CD平分ACB交AB于D，ACB60， BCDDCEACB30 又DEBC
12、， EDCBCD30 故答案是：30 14解：AD是ABC中BAC的平分线，DEAB于点E，DFAC交AC于点F， DFDE2 又SABCSABD+SACD，AB6， 1062+AC2， AC4， 故答案为：4 15解：在ABE和ACF中， ， ABEACF（AAS）， EABFAC， EABBACFACBAC， 12 正确； 没有条件可以证明CDDN， 错误； ABEACF， ABAC， 在ACN和ABM中， ， ACNABM（ASA）， 正确； ABEACF， BECF， 正确 其中正确的结论有 故答案为： 三解答题（共 5 小题） 16（1）证明：ABDCBE， ABCDBE， ABDE
13、，ABBD， ABCDBE（SAS）， BCBE； （2）ABCDBE， DEACAD+DC2.5+2.55，BEBC4， CDP和BEP的周长和DC+DP+CP+BP+PE+BEDC+DE+BC+BE15.5 17解：因为CEBF（已知）， 所以CEBEBFBE（等式的性质）， 即BCEF， 在ABC和DEF中 ， 所以ABCDEF（ASA） 故答案为：BE；等式的性质；BCEF；ASA 18解：（1）BECF， BE+ECCF+EC， BCEF， 在ABC和DEF中 ， ABCDEF（SSS）； （2）ABCDEF， BDEF， ABDE， AEGC 19（1）证明：ABCD， BAEFCD， AFCE， AECF， 又ABCD， ABECDF（SAS） （2）解：BCE30，CBE70， AEBBCE+CBE30+70100， ABECDF， CFDAEB100 20解：（1）由题可得，BDCE2t， CD122t，AE82t， 当AEDC，时，82t（122t）， 解得t3， 故答案为：3； （2）当ABDDCE成立时，ABCD8， 122t8， 解得t2， 运动 2 秒时，ABDDCE能成立； （3）当ABDDCE时，CDEBAD， 又ADE180CDEADB，B180BADADB， ADEB， 又BAC，ABAC， ADEB（180）90 故答案为：90
