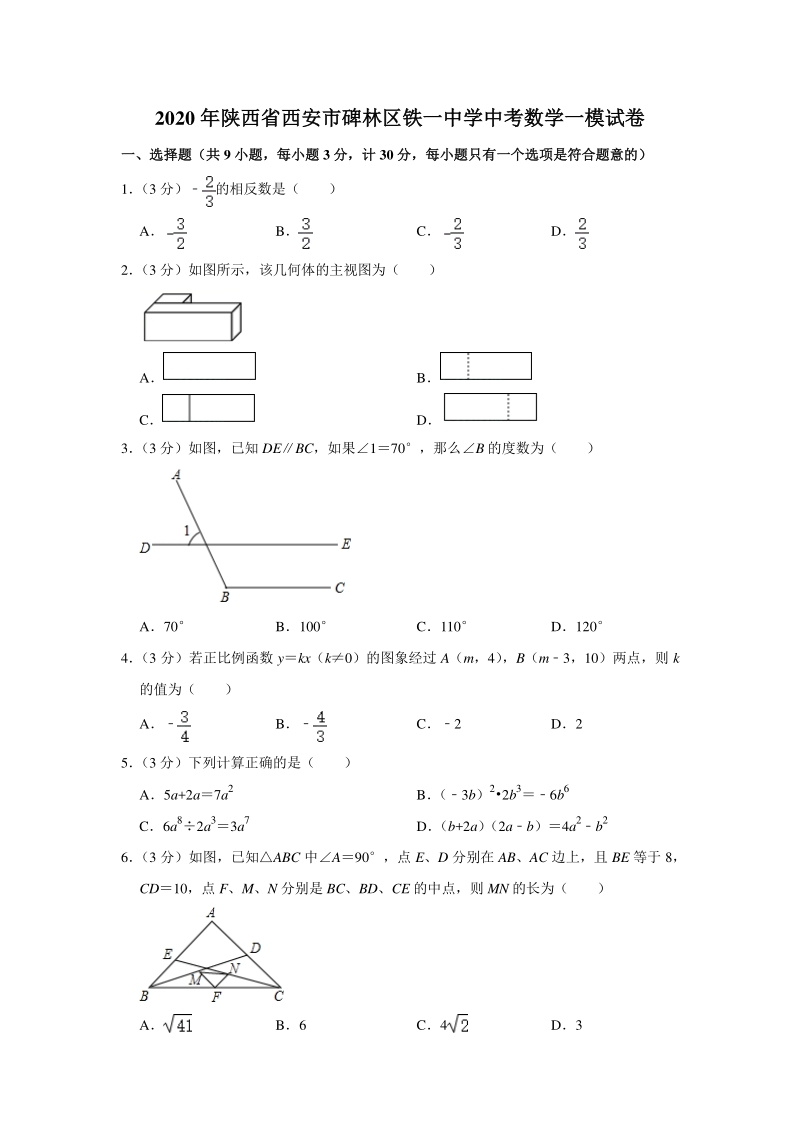
1、2020 年陕西省西安市碑林区铁一中学中考数学一模试卷年陕西省西安市碑林区铁一中学中考数学一模试卷 一、选择题（共一、选择题（共 9 小题，每小题小题，每小题 3 分，计分，计 30 分，每小题只有一个选项是符合题意的）分，每小题只有一个选项是符合题意的） 1 （3 分）的相反数是（ ） A B C D 2 （3 分）如图所示，该几何体的主视图为（ ） A B C D 3 （3 分）如图，已知 DEBC，如果170，那么B 的度数为（ ） A70 B100 C110 D120 4 （3 分）若正比例函数 ykx（k0）的图象经过 A（m，4） ，B（m3，10）两点，则 k 的值为（ ） A
2、B C2 D2 5 （3 分）下列计算正确的是（ ） A5a+2a7a2 B （3b）22b36b6 C6a82a33a7 D （b+2a） （2ab）4a2b2 6 （3 分）如图，已知ABC 中A90，点 E、D 分别在 AB、AC 边上，且 BE 等于 8， CD10，点 F、M、N 分别是 BC、BD、CE 的中点，则 MN 的长为（ ） A B6 C4 D3 7 （3 分）把直线 yx+3 向下平移 a 个单位后，与直线 y2x4 的交点在第四象限，则 a 的取值范围是（ ） A3a5 B1a7 Ca7 Da5 8 （3 分）如图，已知菱形 ABCD 中，ABC135，BFAD 于点
3、 F，BF 交对角线 AC 于点 E， 过点 E 作 EHAB 于点 H， 若EBH 的周长是 2， 则菱形 ABCD 的面积是 （ ） A4 B2 C8 D 9 （3 分）如图，已知四边形 ABCD 内接于O，且O 的半径为 4，连接 AC，BD，交于 点 O，若DAC+BAC90，AB6，则 CD 的长为（ ） A2 B2 C2 D6 二、填空题（共二、填空题（共 4 小题，每小题小题，每小题 3 分，计分，计 12 分）分） 10 （3 分）在实数，0，中，无理数有 11 （3 分）如果一个正多边形的每一个内角都是 144，则该正多边形的对称轴条数 为 12 （3 分）如图，线段 AB
4、交 x 轴于点 C，且 BCAC，点 A 在双曲线 y（x0） 上，点 B 在双曲线 y （k0，x0）上，若OAC 的面积为 4，则 k 的值为 13 （3 分）如图，已知线段 AB8，在平面上有一动点 M 满足 MBMA3，过点 B 作 AMB 角平分线的垂线，垂足为 N，连接 AN，则ANB 面积的最大值为 三、解答题（共三、解答题（共 11 小题，计小题，计 78 分分.解答应写出过程）解答应写出过程） 14 （5 分）计算：4cos30|23| 15 （5 分）解分式方程：3 16 （5 分）如图，已知ABC（BA） ，请在 AC 上求一点 P，使APB+2A180 （保留作图痕迹，
5、不写画法） 17 （5 分） 如图： 已知BE90， 点 B、 C、 F、 E 在一条直线上 ACDF， BFEC 求 证四边形 ACDF 是平行四边形 18 （7 分）识稼穡，会知艰辛；知很辛，会懂检朴；懂俭朴，会远离奢靡，劳动教育成为 大中小学的必修课程，某校建议同学们在家里“停课不停学”的同时也要帮助父母做一 些力所能及的家务小悦随机调查了该校部分同学三份在家做家务的总时间，设被调查得 每位同学三月份在家做家务的总时间为 x 小时，将做家务的总时间分为五个类别：A（0 x6）B（6x12） ，C（12x18） ，D（18x24） ，E（x24） ，并将调查结果 绘成下两幅不完整的统计图，
6、请结合图中信息解答下列问题： （1）在这次活动中被调查的学生共 人； （2）补全条形统计图； （3）该校共有学生 1300 人，根据抽样调查结果，请你估计该校有多少名学生在三月份 在家做家务的时间不低于 12 个小时 19 （7 分）如图，在坡角为 20的山坡上有一铁塔 AB、其正前方矗立着一大型广告牌，当 阳光与水平线成 45角时，测得铁塔 AB 落在斜坡上的影子 BD10 米，落在广告牌上 的影子 CD5 米，已知 AB，CD 均与水平面垂直，请根据相关测量信息，求铁塔 AB 的 高 （sin200.34，cos200.94，tan200.36） 20 （7 分）某校九年级决定购买学习用具
7、对在本次适应性考试中数学成绩进步较大的同学 进行奖励，其中计划购买甲、乙两款圆规套装，已知甲款圆规套装所需费用 y（元）与购 买数量 x（套）之间的函数关系如图所示，乙款圆规套装单价为每套 11 元， （1）求出 y 与 x 的函数关系式； （2） 若购买计划中， 甲、 乙两款圆规套装共需 65 套， 甲款圆规套装的数量不超过 50 套， 但不少于乙款圆规套装的数量，请设计购买方案，使总费用最低，并求出最低费用 21 （7 分）西安城墙国际马拉松赛是世界唯一一个将赛道设置在完整古城墙上的马拉松赛 事，赛事创办于 1993 年，2019 年被正式列入“一带一路”陕西 2019 体育精品赛事行列
8、该赛事共有三项：A （半程马拉松） ：B （13.7 公里） ：C （5 公里） 小林、小远和小斌 参与该赛事的志愿者服务工作，他们每个人被组委会随机的分配到 A、B、C 中的某一个 项目组，每个项目组的志愿者人数不限 （1）求小林被分配到“C （5 公里） ”项目组的概率； （2）已知小林被分配到“A （半程马拉松） ”项目组，请利用列表或画树状图的方法求 出三人被分配到不同项目组的概率为多少？ 22 （8 分）如图，已知ABC 中，ABAC，以 AB 为直径的O 交 CB 于 D，E 为 AB 延长 上一点，C+BDE90 （1）求证：DE 是O 的切线 （2）若 BE2，tanABC，求
9、O 的半径 23 （10 分）如图，在平面直角坐标系中，已知抛物线 C：yax2+bx+c 经过 A（0，3） ， B（2，0）两点，且点 B 为抛物线的顶点 （1）求抛物线 C 的解析式 （2）将抛物线 C 平移到抛物线 C，到抛物线 C的顶点为 B，且与 x 轴交于 M、N（M 在 N 的左侧） ，此时满足以 A、B、B、M 为顶点的四边形面积为 12 的平行四边形，请你写 出平移过程，并说明理由 24 （12 分）问题提出： （1）如图，已知线段 AB 及 AB 外点 C，试在线段 AB 上确定一点 D，使得 CD 最短 问题探究： （2）如图，已知 RtABC 中，ACB90，AB10
10、，sinABC，D 为 AB 中 点，点 E 为 AC 边上的一个动点，请求出BDE 周长的最小值 问题解决： （3）如图，有一个矩形花坛 ABCDAB10m，AD24m，根据设计造型要求，在 AB 上任取一动点 E、连 ED，过点 A 作 AFED，交 DE 于点 F，在 FD 上截取 FP AF，连接 PB、PC；现需在PBC 的区内种植一种黄色花卉，在矩形内的其它区域种植 一种红色花卉，已知种植这种黄色花卉每平方米需 200 元，种植这种红色花卉每平方米 需 180 元，完成这两种花卉的种植至少需花费多少元？（结果保数整数，参考数据： 1.7） 2020 年陕西省西安市碑林区铁一中学中考
11、数学一模试卷年陕西省西安市碑林区铁一中学中考数学一模试卷 参考答案与试题解析参考答案与试题解析 一、选择题（共一、选择题（共 9 小题，每小题小题，每小题 3 分，计分，计 30 分，每小题只有一个选项是符合题意的）分，每小题只有一个选项是符合题意的） 1 （3 分）的相反数是（ ） A B C D 【分析】根据只有符号不同的两个数互为相反数，可得一个数的相反数 【解答】解：的相反数是， 故选：D 2 （3 分）如图所示，该几何体的主视图为（ ） A B C D 【分析】找到从正面看所得到的图形即可 【解答】解：从正面看两个矩形，中间的线为虚线， 故选：B 3 （3 分）如图，已知 DEBC，
12、如果170，那么B 的度数为（ ） A70 B100 C110 D120 【分析】设 DE 与 AB 相交于点 F，由170，可得AFE 的度数，再根据平行线的 性质，即可得到B 的度数 【解答】 解：设 DE 与 AB 相交于点 F， 因为170， 所以AFE110， 因为 DEBC， 所以BAFE110， 故选：C 4 （3 分）若正比例函数 ykx（k0）的图象经过 A（m，4） ，B（m3，10）两点，则 k 的值为（ ） A B C2 D2 【分析】利用一次函数图象上点的坐标特征，可得出关于 k，m 的方程组，解之即可得出 k 值 【解答】解：正比例函数 ykx（k0）的图象经过 A
13、（m，4） ，B（m3，10）两点， ， 解得： 故选：C 5 （3 分）下列计算正确的是（ ） A5a+2a7a2 B （3b）22b36b6 C6a82a33a7 D （b+2a） （2ab）4a2b2 【分析】各项计算得到结果，即可作出判断 【解答】解：A、原式7a，不符合题意； B、原式9b22b318b5，不符合题意； C、原式3a5，不符合题意； D、原式4a2b2，符合题意 故选：D 6 （3 分）如图，已知ABC 中A90，点 E、D 分别在 AB、AC 边上，且 BE 等于 8， CD10，点 F、M、N 分别是 BC、BD、CE 的中点，则 MN 的长为（ ） A B6 C
14、4 D3 【分析】根据三角形中位线定理和勾股定理即可得到结论 【解答】解：A90， ABC+ACB90， 点 F、M、N 分别是 BC、BD、CE 的中点， NFBE，NFBE4，MFCD，MFCD5， NFCABC，MFBACB， MFN180MFBNFC180ABCACB90， MN， 故选：A 7 （3 分）把直线 yx+3 向下平移 a 个单位后，与直线 y2x4 的交点在第四象限，则 a 的取值范围是（ ） A3a5 B1a7 Ca7 Da5 【分析】直线 yx+3 向下平移 a 个单位后可得：yx+3a，求出直线 yx+3a 与直线 y2x4 的交点，再由此点在第四象限可得出 a
15、的取值范围 【解答】解：直线 yx+3 向下平移 a 个单位后可得：yx+3a， 联立两直线解析式得：， 解得：， 即交点坐标为（，） ， 交点在第四象限， ， 解得：1a7 故选：B 8 （3 分）如图，已知菱形 ABCD 中，ABC135，BFAD 于点 F，BF 交对角线 AC 于点 E， 过点 E 作 EHAB 于点 H， 若EBH 的周长是 2， 则菱形 ABCD 的面积是 （ ） A4 B2 C8 D 【分析】由菱形的性质可得DAB45，DACBAC，由角平分线的性质和等腰 直角三角形的性质可得 EFEH，AFBF，ABBF，HEHB，BEBH，由线 段的和差关系可求 EH 的长，
16、可求 AB 和 BF 的长，即可求解 【解答】解：四边形 ABCD 是菱形，ABC135， DAB45，DACBAC， 又 EHAB，EFAD， EFEH，ABFDAB45， AFBF， ABBF， ABF45，EHAB， HEB45ABF， HEHB， BEBH， EBH 的周长是 2， BH+EH+EB2BH+BH2， BH2EHEF， BE22， BFBE+EF， AB2， 菱形 ABCD 的面积ABDH2， 故选：B 9 （3 分）如图，已知四边形 ABCD 内接于O，且O 的半径为 4，连接 AC，BD，交于 点 O，若DAC+BAC90，AB6，则 CD 的长为（ ） A2 B2
17、C2 D6 【分析】由圆周角定理推知 AC、BD 是两直径，所以在直角ABD 中利用勾股定理求得 AD 的长度，然后在直角ADC 中利用勾股定理求得 CD 的长度即可 【解答】解：如图，DAC+BAC90， DAB90 BD 是直径 在直角ABD 中，AB6，BD8，则 AD2 AC 与 BD 相交于点 O AC 是圆 O 的一条直径， ADC90 在直角ADC 中，CD6 故选：D 二、填空题（共二、填空题（共 4 小题，每小题小题，每小题 3 分，计分，计 12 分）分） 10 （3 分）在实数，0，中，无理数有 ， 【分析】无理数常见的三种类型：开方开不尽的数，无限不循环小数，含有 的数
18、 【解答】解：2 是有理数，是有理数，0 是有理数，是无理数，是 无理数， 故答案为：， 11（3 分） 如果一个正多边形的每一个内角都是 144， 则该正多边形的对称轴条数为 10 【分析】根据多边形的内角和公式，得出边数，进而结合对称轴条数的规律，可得答案 【解答】解：设正多边形是 n 边形，由内角和公式得 （n2）180144n， 解得：n10， 故该正多边形的对称轴条数为：10 故答案为：10 12 （3 分）如图，线段 AB 交 x 轴于点 C，且 BCAC，点 A 在双曲线 y（x0） 上，点 B 在双曲线 y（k0，x0）上，若OAC 的面积为 4，则 k 的值为 3 【分析】分
19、别作 ADx 轴于点 D，BEx 轴于点 E，设 A（a，b） ，求得 ab 的值，通过 平行线分线段成比例性质，求得 B 点的坐标，再运用待定系数法求得 k 的值 【解答】解：分别作 ADx 轴于点 D，BEx 轴于点 E，如图， 则 BEAD， 设 A（a，b） ，则 ADb，ODa， 点 A 在双曲线 y（x0）上， ab12， ， OAC 的面积为 4， OC2CD， BEAD，BCAC， ， BEADb，CE， OEOCCE2CDCDCD， DECE+CD， OEDECDa， B（a，b） ， 点 B 在双曲线 y（k0，x0）上， k3 故答案为：3 13 （3 分）如图，已知线段
20、 AB8，在平面上有一动点 M 满足 MBMA3，过点 B 作 AMB 角平分线的垂线，垂足为 N，连接 AN，则ANB 面积的最大值为 6 【分析】延长 BM、MA 交于点 C，过点 N 作 NHAB 于 H，取 AB 的中点 P，连接 PN， 易证CNMBNM，则有 BNCN，MBMC，由 MBMA3 可得 AC3，根据三 角形中位线定理可得 PN，根据点到直线之间垂线段最短可得 NH，从而可求出 ANB 的面积的最大值 【解答】解：延长 BM、MA 交于点 C，过点 N 作 NHAB 于 H，取 AB 的中点 P，连接 PN，如图 MN 平分AMB，BNMN， AMNBMN，CNMBNM
21、90 在CNM 和BNM 中， ， CNMBNM（ASA） ， BNCN，MBMC MBMA3， AC3， BCPCPBPAPB4 BNCN，BPAP， PNAC NHAB， NH 当 ACAB 时，NP 与 NH 重合，此时，NH 取得最大值， ANB 的面积也就取到最大值，最大值为6 故答案为 6 三、解答题（共三、解答题（共 11 小题，计小题，计 78 分分.解答应写出过程）解答应写出过程） 14 （5 分）计算：4cos30|23| 【分析】先计算立方根、代入三角函数值、去绝对值符号，再去括号，最后计算加减可 得 【解答】解：原式34（32） 323+2 33 15 （5 分）解分式
22、方程：3 【分析】分式方程去分母转化为整式方程，求出整式方程的解得到 x 的值，经检验即可 得到分式方程的解 【解答】解：去分母得：3x29x2x63x227， 解得：x， 经检验 x是分式方程的解 16 （5 分）如图，已知ABC（BA） ，请在 AC 上求一点 P，使APB+2A180 （保留作图痕迹，不写画法） 【分析】根据线段垂直平分线的性质即可在 AC 上求一点 P，使APB+2A180 【解答】解：如图， 点 P 即为所求 17 （5 分） 如图： 已知BE90， 点 B、 C、 F、 E 在一条直线上 ACDF， BFEC 求 证四边形 ACDF 是平行四边形 【分析】证 RtA
23、BCRtDEF（HL） ，得出ACBDFE，则ACFDFC，证出 ACDF，再由 ACDF，即可得出四边形 ACDF 是平行四边形 【解答】证明：BFEC， BFCFECCF，即 BCEF， 在 RtABC 和 RtDEF 中， RtABCRtDEF（HL） ， ACBDFE， ACFDFC， ACDF， 又ACDF， 四边形 ACDF 是平行四边形 18 （7 分）识稼穡，会知艰辛；知很辛，会懂检朴；懂俭朴，会远离奢靡，劳动教育成为 大中小学的必修课程，某校建议同学们在家里“停课不停学”的同时也要帮助父母做一 些力所能及的家务小悦随机调查了该校部分同学三份在家做家务的总时间，设被调查得 每位
24、同学三月份在家做家务的总时间为 x 小时，将做家务的总时间分为五个类别：A（0 x6）B（6x12） ，C（12x18） ，D（18x24） ，E（x24） ，并将调查结果 绘成下两幅不完整的统计图，请结合图中信息解答下列问题： （1）在这次活动中被调查的学生共 50 人； （2）补全条形统计图； （3）该校共有学生 1300 人，根据抽样调查结果，请你估计该校有多少名学生在三月份 在家做家务的时间不低于 12 个小时 【分析】 （1）根据 A 类的人数和所占的百分比即可得出答案； （2）用总人数减去其它类的人数求出 D 类的人数，从而补全统计图； （3） 用该校的总人数乘以在家做家务的时间不
25、低于12个小时的人数所占的百分比即可 【解答】解： （1）在这次活动中被调查的学生总人数有：1020%50（人） ， 故答案为：50； （2）D 类人数：5010141646（人） ， 补全条形统计图如下： （3）根据题意得： 1300（120%28%）676（名） ， 答：估计该校有 676 名学生在三月份在家做家务的时间不低于 12 个小时 19 （7 分）如图，在坡角为 20的山坡上有一铁塔 AB、其正前方矗立着一大型广告牌，当 阳光与水平线成 45角时，测得铁塔 AB 落在斜坡上的影子 BD10 米，落在广告牌上 的影子 CD5 米，已知 AB，CD 均与水平面垂直，请根据相关测量信息
26、，求铁塔 AB 的 高 （sin200.34，cos200.94，tan200.36） 【分析】过点 C 作 CEAB 于 E，过点 B 作 BNCD 于 N，在 RtBND 中，分别求出 DN、BN 的长度，在 RtACE 中，求出 AE、CE 的长度，继而可求得 AB 的长度 【解答】解：过点 C 作 CEAB 于 E，过点 B 作 BNCD 于 N， 在 RtBND 中， DBN20，BD10， DNBDsinDBN100.343.4， BNBDcosDBN100.949.4， ABCD，CEAB，BNCD， 四边形 BNCE 为矩形， BNCE9.4，CNBECDDN1.6， 在 Rt
27、ACE 中，ACE45， AECE9.4， AB9.4+1.611（米） 答：铁塔 AB 的高约为 11 米 20 （7 分）某校九年级决定购买学习用具对在本次适应性考试中数学成绩进步较大的同学 进行奖励，其中计划购买甲、乙两款圆规套装，已知甲款圆规套装所需费用 y（元）与购 买数量 x（套）之间的函数关系如图所示，乙款圆规套装单价为每套 11 元， （1）求出 y 与 x 的函数关系式； （2） 若购买计划中， 甲、 乙两款圆规套装共需 65 套， 甲款圆规套装的数量不超过 50 套， 但不少于乙款圆规套装的数量，请设计购买方案，使总费用最低，并求出最低费用 【分析】 （1）根据函数图象中的
28、数据可以求得 y 与 x 的函数关系式； （2）根据（1）中的函数关系式和题意，可以求得费用的最小值和所对应的的购买方案 【解答】解： （1）当 0 x30 时，设 y 与 x 的函数关系式为 yk1x， 30k1360， 解得，k112， 即当 0 x30 时，y 与 x 的函数关系式为 y12x， 当 x30 时，设 y 与 x 的函数关系式是 yk2x+b， ， 解得， 即当 x30 时，y 与 x 的函数关系式是 y10 x+60， 综上可知：y 与 x 的函数关系式为 y； （2）设购买甲款圆规套装的数量 x 套，则购买乙款圆规套装的数量是（65x）支， 由甲款圆规套装的数量不超过
29、50 套，但不少于乙款圆规套装的数量，得 ， 解得 32.5x50， x 为整数， 33x50， 设总费用为 W 元， 当 x30 时，y 与 x 的函数关系式是 y10 x+60， W11（65x）+（10 x+60）x+775， 以为 k10，所以 W 随 x 的增大而减小， 故当 x50 时，W 取得最小值，此时 W725，65x15， 答：当购买甲款圆规套装 50 套，B 种乙款圆规套装 15 套时总费用最低，最低费用是 725 元 21 （7 分）西安城墙国际马拉松赛是世界唯一一个将赛道设置在完整古城墙上的马拉松赛 事，赛事创办于 1993 年，2019 年被正式列入“一带一路”陕西
30、 2019 体育精品赛事行列 该赛事共有三项：A （半程马拉松） ：B （13.7 公里） ：C （5 公里） 小林、小远和小斌 参与该赛事的志愿者服务工作，他们每个人被组委会随机的分配到 A、B、C 中的某一个 项目组，每个项目组的志愿者人数不限 （1）求小林被分配到“C （5 公里） ”项目组的概率； （2）已知小林被分配到“A （半程马拉松） ”项目组，请利用列表或画树状图的方法求 出三人被分配到不同项目组的概率为多少？ 【分析】 （1）利用概率公式直接计算即可； （2）根据树状图，可得所有可能的结果，即可求出三人被分配到不同项目组的概率 【解答】解： （1）赛事共有三项， 小林被分配到
31、“C （5 公里） ”项目组的概率为； （2）小林被分配到“A （半程马拉松） ”项目组， 画树状图如下： 由树状图可知： 所有等可能的结果有 9 种， 小林被分配到 A， 小远和小斌被分配到 B、C 组的情况有 2 种， 所以三人被分配到不同项目组的概率为 22 （8 分）如图，已知ABC 中，ABAC，以 AB 为直径的O 交 CB 于 D，E 为 AB 延长 上一点，C+BDE90 （1）求证：DE 是O 的切线 （2）若 BE2，tanABC，求O 的半径 【分析】 （1）连接 OD，证得ODB+BDE90，则ODE90，可得出结论； （2）连接 AD，证明BDEDEA，可求出 DE，
32、AE 的长，则 AB 可求出则答案可 得出 【解答】解： （1）证明：连接 OD， ABAC， CABC， C+BDE90， ABC+BDE90， ODOB， OBDODB， ODB+BDE90， ODE90， 即 ODDE， DE 是O 的切线； （2）连接 AD， AB 是O 的直径， ADB90， BAD+ABD90， BDE+ABD90， BDEBAD， BDEDEA， ， tanABC， ， ， BE2， DE2，AE10， AB1028， O 的半径为 4 23 （10 分）如图，在平面直角坐标系中，已知抛物线 C：yax2+bx+c 经过 A（0，3） ， B（2，0）两点，且点
33、 B 为抛物线的顶点 （1）求抛物线 C 的解析式 （2）将抛物线 C 平移到抛物线 C，到抛物线 C的顶点为 B，且与 x 轴交于 M、N（M 在 N 的左侧） ，此时满足以 A、B、B、M 为顶点的四边形面积为 12 的平行四边形，请你写 出平移过程，并说明理由 【分析】 （1）利用顶点式解决问题即可 （2）分点 M 在点 B 的右边或左边两种情形分别求解即可 【解答】解： （1）抛物线的顶点为 B（2，0） ， 可以假设抛物线的解析式为 ya（x2）2， 把 A（0，3）代入 ya（x2）2，得到 a 抛物线的解析式为 y（x2）2 （2）当点 M 在点 B 的左侧时， 四边形 ABBM
34、 是平行四边形时， ABBM，ABMB， 点 B的纵坐标与点 A 的纵坐标绝对值相等， A（0，3） ， 点 B的纵坐标为 3， 平行四边形 ABBM 的面积为 12， SBMBBM36， BM4， B（2，0） ， M（2，0） ，B（0，3） ， 抛物线 C 向左平移 2 个单位，再向上平移 3 个单位得到抛物线 C， 同理可得，当点 M 在点 B 的右侧时，M（6，0） ，B（8，3） ， 抛物线 C 向右平移 6 个单位，再向上平移 3 个单位得到抛物线 C 24 （12 分）问题提出： （1）如图，已知线段 AB 及 AB 外点 C，试在线段 AB 上确定一点 D，使得 CD 最短
35、问题探究： （2）如图，已知 RtABC 中，ACB90，AB10，sinABC，D 为 AB 中 点，点 E 为 AC 边上的一个动点，请求出BDE 周长的最小值 问题解决： （3）如图，有一个矩形花坛 ABCDAB10m，AD24m，根据设计造型要求，在 AB 上任取一动点 E、连 ED，过点 A 作 AFED，交 DE 于点 F，在 FD 上截取 FP AF，连接 PB、PC；现需在PBC 的区内种植一种黄色花卉，在矩形内的其它区域种植 一种红色花卉，已知种植这种黄色花卉每平方米需 200 元，种植这种红色花卉每平方米 需 180 元，完成这两种花卉的种植至少需花费多少元？（结果保数整数
36、，参考数据： 1.7） 【分析】 （1）根据垂线段最短解决问题即可 （2） 如图中， 作点 D 关于 AC 的对称点 D， 连接 DD交 AC 于 J， 连接 ED， BD， 过点 D作 DHBC 交 BC 的延长线于 H周长 DE+EB 的最小值即可解决问题 （3）如图中，以 AD 为边向上作等边三角形 ADJ，作AJ 的外接圆J，在J 上取 一点 T，连接 TA，TD，过点 J 作 JQBC 于 Q，过点 P 作 PHBC 于 H求出 PH 的最 小值即可解决问题 【解答】解： （1）如图中，线段 CD 即为所求 （2） 如图中， 作点 D 关于 AC 的对称点 D， 连接 DD交 AC
37、于 J， 连接 ED， BD， 过点 D作 DHBC 交 BC 的延长线于 H 在 RtACB 中，ACB90，AB10， sinABC， AC8，BC6， DJAACB90， DJBC， ADDB， AJJC4， DJJDBC3，AJJC4， DHCHCJCJD90， 四边形 CHDJ 是矩形， JDCH3，DHJC4， BHBC+CH6+39， BD， DE+BEBE+EDBD， DE+BE， DE+BE 的最小值为， BDE 的周长的最小值为 5+ （3）如图中，以 AD 为边向上作等边三角形 ADJ，作AJ 的外接圆J，在J 上取 一点 T，连接 TA，TD，过点 J 作 JQBC 于 Q，过点 P 作 PHBC 于 H 在 RtAFP 中，tanAPF， APF30， APD150， ADJ 是等边三角形， AJD60， TAJD30， T+APD180， A，T，D，P 四点共圆， AB10m，ADAJJDAP24m， AQ（10+12） （m） ， PA+PHAQ， PH 的最小值（10+12）24（1214） （m） ， 完成这两种花卉的种植的费用20024PH+180（102424PH） 240PH+43200， PH1214 时，费用最小，最小值为 240（1214）+4320044736（元）
