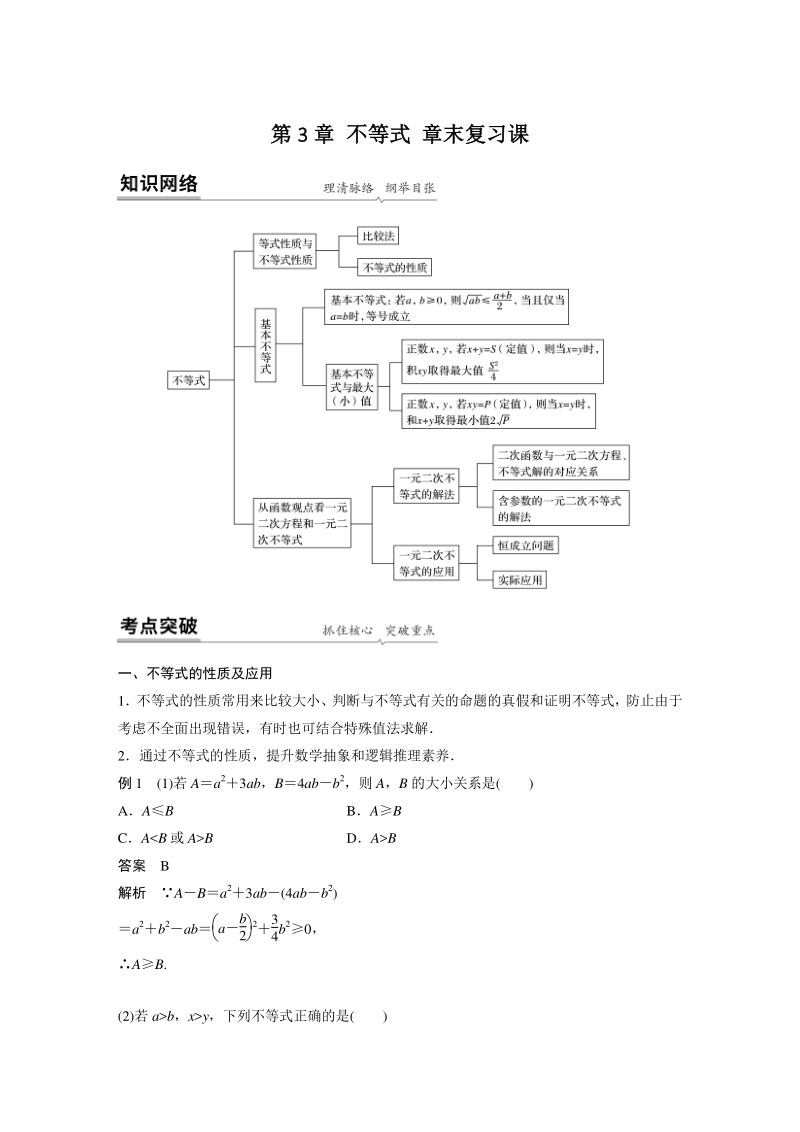
1、第第 3 3 章章 不等式不等式 章末复习课章末复习课 一、不等式的性质及应用 1不等式的性质常用来比较大小、判断与不等式有关的命题的真假和证明不等式，防止由于 考虑不全面出现错误，有时也可结合特殊值法求解 2通过不等式的性质，提升数学抽象和逻辑推理素养 例 1 (1)若 Aa23ab，B4abb2，则 A，B 的大小关系是( ) AAB BAB CAB DAB 答案 B 解析 ABa23ab(4abb2) a2b2ab ab 2 23 4b 20， AB. (2)若 ab，xy，下列不等式正确的是( ) Aaxby C|a|x|a|y D(ab)x0，不等式两边同乘以一个大于零的数，不等号方
2、向不变；当 a 0 时，|a|x|a|y，故|a|x|a|y. 反思感悟 不等式性质的应用方法 (1)作差法比较大小的关键是对差式进行变形，变形的方法一般是通分、分解因式、配方等 (2)不等式真假的判断，要依靠其适用范围和条件来确定，举反例是判断命题为假的一个好方 法，用特例法验证时要注意，适合的不一定对，不适合的一定错，故特例只能否定选择项 跟踪训练 1 已知 a，b，c，dR，则 Pacbd，Q a2b2c2d2的大小关系为( ) APQ BPQ CP0 的解集是 x 1 2xa5 的解集 解 (1)依题意，可得 ax25x20 的两个实数根为1 2和 2， 由根与系数的关系，得 1 22
3、 2 a ， 1 22 5 a 解得 a2. (2)将 a2 代入不等式，得12x x1 3， 即12x x1 30， 整理得x2 x1 0，即(x1)(x2)0， 解得2x1， 则不等式的解集为x|2x0，b0)是每年高考的热点，主要考查命题判断、不等式证明 以及求最值问题，特别是求最值问题往往与实际问题相结合，同时在基本不等式的使用条件 上设置一些问题，实际上是考查学生恒等变形的技巧，另外，基本不等式的和与积的转化在 高考中也经常出现 2借助基本不等式的应用，提升数学抽象和数学运算素养 例 3 (1)若 0x2，则 x(2x)的最大值是( ) A2 B.3 2 C1 D. 1 2 答案 C
4、 解析 因为 0x0，x(2x) x2x 2 21， 当且仅当 x2x，即 x1 时，等号成立 (2)已知 x0，y0，且 x3y1，则xy xy 的最小值是_ 答案 2 34 解析 x0，y0，且 x3y1. xy xy xyx3y xy x 23y24xy xy x 23y2 xy 42 x 2 3y2 xy 42 34. 当且仅当 x 3y，x3y1， 即 y 1 3 3 3 3 6 ，x 3 3 3 31 2 时取等号 xy xy 的最小值是 2 34. 反思感悟 利用基本不等式求最值的关注点 (1)注意寻求已知条件与目标函数之间的联系 (2)利用添项和拆项的配凑方法，使积(或和)产生
5、定值特别注意“1”的代换 跟踪训练 3 已知函数 yx4 9 x1(x1)， 当 xa 时， y 取得最小值 b， 则 a_； b_. 答案 2 1 解析 yx4 9 x1(x1) 9 x15， 因为 x1，所以 x10， 所以 y2x1 9 x152351， 当且仅当 x1 9 x1，即 x2 时，等号成立， 此时 a2，b1. 四、不等式在实际问题中的应用 1不等式的应用题常以函数为背景，多是解决现实生活、生产中的优化问题，在解题中主要 涉及不等式的解法、基本不等式求最值，根据题设条件构建数学模型是解题关键 2利用不等式解决实际应用问题，提升数学建模素养和数学运算素养 例4 某房地产开发公
6、司计划在一楼区内建造一个长方形公园ABCD， 公园由长方形A1B1C1D1 的休闲区和环公园人行道(阴影部分)组成已知休闲区 A1B1C1D1的面积为 4 000 平方米，人 行道的宽分别为 4 米和 10 米(如图所示) (1)若设休闲区的长和宽的比A1B1 B1C1x(x1)，写出公园 ABCD 所占面积 S 与 x 的关系式； (2)要使公园所占面积最小，则休闲区 A1B1C1D1的长和宽该如何设计？ 解 (1)设休闲区的宽 B1C1为 a 米，则长 A1B1为 ax 米，由 a2x4 000，得 a20 10 x . 则 S(a8)(ax20)a2x(8x20)a160 4 000(8
7、x20) 20 10 x 160 80 10 2 x 5 x 4 160(x1) (2)80 10 2 x 5 x 4 160 80 1022 x 5 x4 160 1 6004 1605 760. 当且仅当 2 x 5 x，即 x2.5 时，等号成立， 此时 a40，ax100. 所以要使公园所占面积最小，休闲区 A1B1C1D1应设计为长 100 米，宽 40 米 反思感悟 解决与不等式有关的实际应用问题的关注点 (1)审题要准，初步建模 (2)设出变量，列出函数关系式 (3)根据题设构造应用不等式的形式并解决问题 跟踪训练 4 甲厂以 x 千克/小时的速度运输生产某种产品(生产条件要求
8、1x10)，每小时 可获得的利润是 100 5x13 x 元 (1)要使生产该产品 2 小时获得的利润不低于 3 000 元，求 x 的取值范围； (2)要使生产 900 千克该产品获得的利润最大，问：甲厂应该选取何种生产速度？并求最大利 润 解 (1)根据题意，200 5x13 x 3 000 5x143 x0， 又 1x10，可解得 3x10. (2)设利润为 y 元，则 y900 x 100 5x13 x 9104 3 1 x 1 6 261 12 ， 故 x6 千克/小时时，ymax457 500 元 1(2020 全国)已知集合 Ax|x23x40，B4,1,3,5，则 AB 等于(
9、 ) A4,1 B1,5 C3,5 D1,3 答案 D 解析 Ax|x23x40 x|(x1)(x4)0 x|1x0，Bx|x10，则 AB 等于( ) Ax|x1 Bx|2x1 Cx|3x3 答案 A 解析 根据题意知，Ax|x25x60 x|x3 或 x2，Bx|x10 x|x1，则 AB x|x0，则RA 等于( ) Ax|1x2 Bx|1x2 Cx|x2 Dx|x1x|x2 答案 B 解析 x2x20，(x2)(x1)0，x2 或 x2 或 x0 在 R 上恒成立，则实数 a 的取值范围是 _ 答案 (0,8) 解析 x2ax2a0 在 R 上恒成立， a242a0，0a0，则a 44b41 ab 的最小值为_ 答案 4 解析 a，bR，ab0， a 44b41 ab 4a 2b21 ab 4ab 1 ab2 4ab 1 ab4， 当且仅当 a22b2， 4ab 1 ab， 即 a2 2 2 ， b2 2 4 ab0 时取得等号 故a 44b41 ab 的最小值为 4.
