 陕西省西安交大附中2020年中考数学三模试卷(含答案解析)
陕西省西安交大附中2020年中考数学三模试卷(含答案解析)
《陕西省西安交大附中2020年中考数学三模试卷(含答案解析)》由会员分享,可在线阅读,更多相关《陕西省西安交大附中2020年中考数学三模试卷(含答案解析)(27页珍藏版)》请在七七文库上搜索。
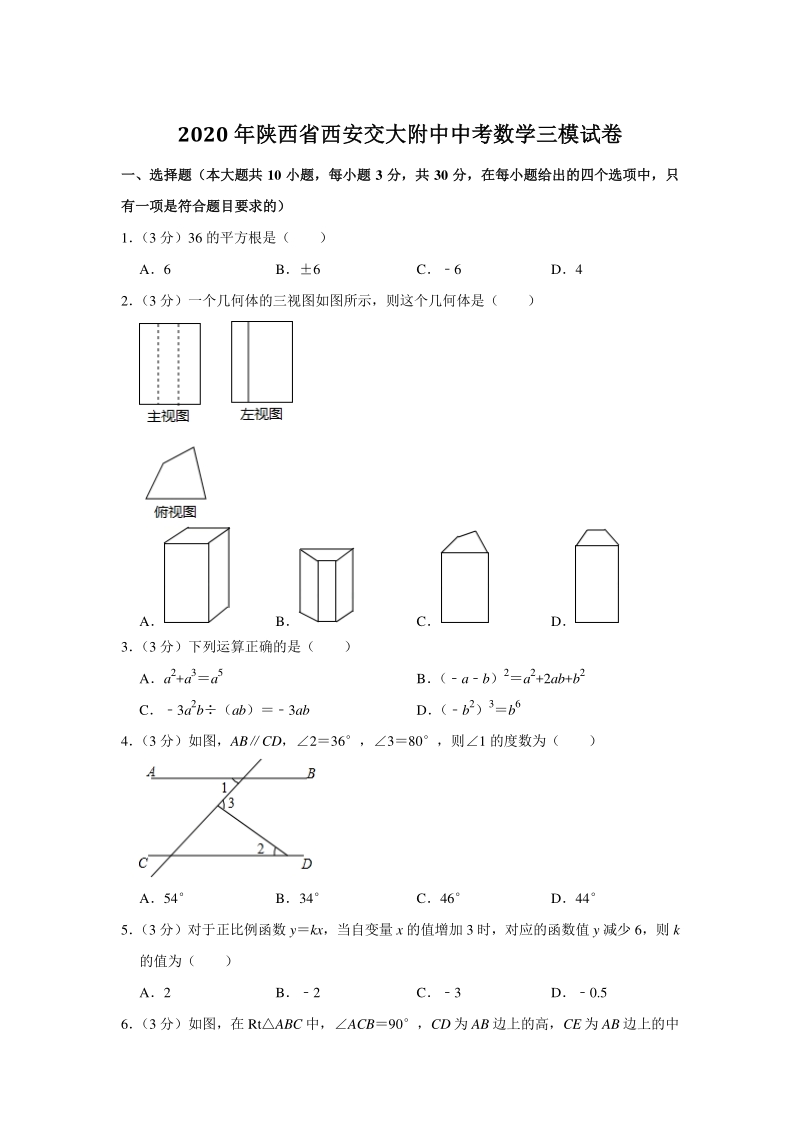
1、2020 年陕西省西安交大附中中考数学三模试卷年陕西省西安交大附中中考数学三模试卷 一、选择题(本大题共一、选择题(本大题共 10 小题,每小题小题,每小题 3 分,共分,共 30 分,在每小题给出的四个选项中,只分,在每小题给出的四个选项中,只 有一项是符合题目要求的)有一项是符合题目要求的) 1 (3 分)36 的平方根是( ) A6 B6 C6 D4 2 (3 分)一个几何体的三视图如图所示,则这个几何体是( ) A B C D 3 (3 分)下列运算正确的是( ) Aa2+a3a5 B (ab)2a2+2ab+b2 C3a2b(ab)3ab D (b2)3b6 4 (3 分)如图,AB
2、CD,236,380,则1 的度数为( ) A54 B34 C46 D44 5 (3 分)对于正比例函数 ykx,当自变量 x 的值增加 3 时,对应的函数值 y 减少 6,则 k 的值为( ) A2 B2 C3 D0.5 6 (3 分)如图,在 RtABC 中,ACB90,CD 为 AB 边上的高,CE 为 AB 边上的中 线,AD2,CE5,则 CD( ) A2 B3 C4 D2 7(3 分) 已知一次函数 ymx+4 与一次函数 y2x+n 关于 x 轴对称, 则 m、 n 分别为 ( ) Am2,n4 Bm2,n4 Cm2,n4 Dm2,n4 8 (3 分)如图,点 O 是矩形 ABC
3、D 的对称中心,点 E 在 AB 边上,连接 CE若点 B 与点 O 关于 CE 对称,则 CB:AB 为( ) A B C D 9 (3 分)如图,四边形 ABCD 内接于圆 O,连接 OB,OD,若BODBCD,则BAD 的度数为( ) A30 B45 C60 D120 10 (3 分)已知二次函数 yax2+2ax+2a+5(其中 x 是自变量)图象上有两点(2,y1) , (1,y2) ,满足 y1y2当2x1 时,y 的最小值为5,则 a 的值为( ) A5 B10 C2 D5 二二.填空题(本大题共填空题(本大题共 4 个小题,每小题个小题,每小题 3 分,共分,共 12 分)分)
4、 11 (3 分)不等式 12x4 的负整数解是 12 (3 分) 某正多边形外接圆的半径为 4, 边心距为 2, 则该正多边形的边长为 13 (3 分)如图,在平面直角坐标系 xOy 中,矩形 OABC 的两边 OC、OA 分别在 x 轴、y 轴的正半轴上,反比例函数 y(x0)分别与边 AB、边 BC 相交于点 E、点 F,且点 E、 点 F 分别为 AB、 BC 边的中点, 连接 EF 若BEF 的面积为 3, 则 k 的值是 14 (3 分)如图,在 RtABC 中,ACB90,AB4,以 AC 为边在ABC 外作等边 三角形ACD,连接 BD则 BD 的最大值是 三三.解答题(本大题
5、共解答题(本大题共 11 小题,共小题,共 78 分,解答应写出过程)分,解答应写出过程) 15 (5 分)计算: () 2|tan602|+ 16 (5 分)化简并求值: (1),其中 x1 17 (5 分)如图,已知ABC 中,ABAC,BAC 的平分线 AD 交 BC 于 D请用尺规在 AD 上找一点 P,使得点 P 到 AB 的距离等于 PD (保留作图痕迹,不写做法) 18 (5 分)如图,点 D、C 在线段 BF 上,BDCF,BF,且 DEAC求证:AC DE 19 (7 分)近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查,调查 结果显示,支付方式有:A 微信、B
6、 支付宝、C 现金、D 其他该小组对某超市一天内购 买者的支付方式进行调查统计,得到如下两幅不完整的统计图 请你根据统计图提供的信息,解答下列问题: (1)补全条形统计图; (2)在扇形统计图中,A 种支付方式所对应的圆心角为 度 (3)若该超市这一周内有 1500 名购买者,请你估计使用 A 和 B 两种支付方式的购买者 共有多少名? 20 (7 分)小华和同学们想用一些测量工具和所学的几何知识测量学校旗杆的高度 PA,检 验自己掌握知识和运用知识的能力如图所示,旗杆直立于旗台上的点 P 处,他们的测 量方法是:首先,在阳光下,小华站在旗杆影子的顶端 F 处此时,量的小华的影长 FG 2m
7、小华身高 EF1.6m;然后,在旗杆影子上的点 D 处,安装测频器 CD测得旗杆 顶端 A 的仰角为 49,量得 CD0.6m,DF5m,旗台高 BP1.2m已知在测量过程 中,点 B、D、F、G 在同一水平直线上,点 A、P、B 在同一条直线上,AB、CD、EF 均 垂直于 BG,求旗杆的高度 PA(参考数据:sin490.8,cos490.7tan491.2) 21 (7 分)小蕊骑电动车,小彤骑自行车分别同时从 A、B 两地出发,匀速相向而行,在 45 分钟时两人相遇,在行驶的过程中,小蕊到达 B 地后停留一会,再按原路原速返回 A 地,小彤一直匀速骑自行车 3h 后,与小蕊同时到达 A
8、 地,如图表示两人距 B 地的距离 y (km)与时间 x(h)之间的函数关系 (1)求小蕊和小彤骑车的速度; (2)求线段 AB 的解析式; (3)如果小蕊不在 B 地停留,按原路原速直接返回,问在小蕊回到 A 地之前,小蕊何时 能追上小彤? 22 (7 分) “新冠肺炎”肆虐,无数抗疫英雄涌现,以下四位抗疫英雄是钟南山、李兰娟、 李文亮、张定宇(依次记为 A、B、C、D) 为让同学们了解四位的事迹,老师设计如下 活动:取四张完全相同的卡片,分别写上 A、B、C、D 四个标号,然后背面朝上放置, 搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡 片上的标号查找相应
9、抗疫英雄的资料,并做成小报 (1)班长在四种卡片中随机抽到标号为 C 的概率为 (2) 平平和安安两位同学抽到的卡片是不同英雄的概率是多少?用树状图或列表的方法 表示 23 (8 分)如图,点 A,点 C 在以 BD 为直径的O 上过点 A 作 AEBC 交 CD 的延长线 于点 E,且DAEABD (1)求证:AE 是O 的切线 (2)若O 的半径为 5CD6,求 AD 的长 24 (10 分)在平面直角坐标系中,O 为坐标原点,抛物线 L:yax24ax(a0)与 x 轴 正半轴交于点 A抛物线 L 的顶点为 M,对称轴与 x 轴交于点 D (1)求抛物线 L 的对称轴 (2)抛物线 L:
10、yax24ax 关于 x 轴对称的抛物线记为 L,抛物线 L的顶点为 M,若 以 O、M、A、M为顶点的四边形是正方形,求 L的表达式 (3)在(2)的条件下,点 P 在抛物线 L 上,且位于第四象限,点 Q 在抛物线 L上,是 否存在点 P、点 Q 使得以 O、D、P、Q 为顶点的四边形是平行四边形,若存在,求出点 P 坐标,若不存在,请说明理由 25 (12 分)问题提出: (1)如图,已知ABC 中,点 D 在 BC 边上,且 BD2CD连接 AD,则 SABD:S ACD 问题探究: (2)如图,已知 AD 是ABC 的中线,过点 D 任意做一条直线交 AB 于点 E,交 AC 延长线
11、于点 F请说明 SAEFSABC 问题解决: (3)如图,有一个菱形花园 ABCD,B60,AB80 米在对角线 AC 上有一个 凉亭 P,测得 PC30 米,按规划,过凉亭 P 要修建一条笔直的小路 EF,使得点 E 在 BC 边上,点 F 在 CD 边上,连接 AE、AF在四边形 AECF 中种植花卉,在菱形内其他区域 种植草坪 已知花卉每平米 400 元, 草坪每平米 120 元若要花园中全部种植草坪和花卉, 则所需费用至少为多少元?(小路的宽度忽略不计,结果保留整数,1.7) 2020 年陕西省西安交大附中中考数学三模试卷年陕西省西安交大附中中考数学三模试卷 参考答案与试题解析参考答案
12、与试题解析 一、选择题(本大题共一、选择题(本大题共 10 小题,每小题小题,每小题 3 分,共分,共 30 分,在每小题给出的四个选项中,只分,在每小题给出的四个选项中,只 有一项是符合题目要求的)有一项是符合题目要求的) 1 (3 分)36 的平方根是( ) A6 B6 C6 D4 【分析】根据平方根的定义求解即可 【解答】解:(6)236, 36 的平方根是6, 故选:B 2 (3 分)一个几何体的三视图如图所示,则这个几何体是( ) A B C D 【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形 【解答】解:由于主视图和左视图为长方形可得此几何体为柱体, 由
13、俯视图为四边形,只有 C 符合条件; 故选:C 3 (3 分)下列运算正确的是( ) Aa2+a3a5 B (ab)2a2+2ab+b2 C3a2b(ab)3ab D (b2)3b6 【分析】直接利用合并同类项法则、乘法公式以及积的乘方运算法则、整式的除法运算 法则分别判断得出答案 【解答】解:A、a2+a3,不是同类项,无法合并,故此选项错误; B、 (ab)2a2+2ab+b2,故此选项正确; C、3a2b(ab)3a,故此选项错误; D、 (b2)3b6,故此选项错误; 故选:B 4 (3 分)如图,ABCD,236,380,则1 的度数为( ) A54 B34 C46 D44 【分析】
14、利用平行线的性质三角形的外角的性质解决问题即可 【解答】解:如图,ABCD, 14, 34+2,236,380, 444, 144, 故选:D 5 (3 分)对于正比例函数 ykx,当自变量 x 的值增加 3 时,对应的函数值 y 减少 6,则 k 的值为( ) A2 B2 C3 D0.5 【分析】由于自变量 x 增加 3,y 的值减小 6,则 y6k(x+3) ,然后把 ykx 代入可求 出 k 的值 【解答】解:根据题意得 y6k(x+3) , 即 y6kx+3k, 而 ykx, 所以 kx6kx+3k 3k6 解得:k2 故选:B 6 (3 分)如图,在 RtABC 中,ACB90,CD
15、 为 AB 边上的高,CE 为 AB 边上的中 线,AD2,CE5,则 CD( ) A2 B3 C4 D2 【分析】根据直角三角形的性质得出 AECE5,进而得出 DE3,利用勾股定理解答 即可 【解答】解:在 RtABC 中,ACB90,CE 为 AB 边上的中线,CE5, AECE5, AD2, DE3, CD 为 AB 边上的高, 在 RtCDE 中,CD, 故选:C 7(3 分) 已知一次函数 ymx+4 与一次函数 y2x+n 关于 x 轴对称, 则 m、 n 分别为 ( ) Am2,n4 Bm2,n4 Cm2,n4 Dm2,n4 【分析】一次函数 ymx+4 与一次函数 y2x+n
16、 关于 x 轴对称,则两函数相交于 x 轴上 一点,所以令两方程中 y0,分别解得 x,令其相等即可 【解答】解:根据题意,n4, 一次函数 ymx+4 与一次函数 y2x4, 在 y2x4 中,令 y0,则 02x4,解得 x2, 两函数交于点(2,0) , 把(2,0)代入 ymx+4 得:02m+4 解得:m2, 故选:B 8 (3 分)如图,点 O 是矩形 ABCD 的对称中心,点 E 在 AB 边上,连接 CE若点 B 与点 O 关于 CE 对称,则 CB:AB 为( ) A B C D 【分析】连接 DB,利用对称得出 OEEB,进而利用全等三角形的判定和性质得出 OC BC,进而
17、解答即可 【解答】解:连接 DB,AC,OE, 四边形 ABCD 是矩形, ACDB,ABC90,OCOAOBOD, 点 B 与点 O 关于 CE 对称, OEEB,OECBEC, 在COE 与CBE 中, , COECBE(SAS) , OCCB, AC2BC, ABC90, ABCB, 即 CB:AB, 故选:C 9 (3 分)如图,四边形 ABCD 内接于圆 O,连接 OB,OD,若BODBCD,则BAD 的度数为( ) A30 B45 C60 D120 【分析】根据圆内接四边形的性质,构建方程解决问题即可 【解答】解:设BADx,则BOD2x, BCDBOD2x,BAD+BCD180,
18、 3x180, x60, BAD60, 故选:C 10 (3 分)已知二次函数 yax2+2ax+2a+5(其中 x 是自变量)图象上有两点(2,y1) , (1,y2) ,满足 y1y2当2x1 时,y 的最小值为5,则 a 的值为( ) A5 B10 C2 D5 【分析】将点的坐标代入解析式,可求 a0,由取值范围可求当 x1 时,y 有最小值, 即可求解 【解答】 解: 当 x2 时, y14a4a+2a+52a+5, 当 x1 时, y2a+2a+2a+55a+5, y1y2, 2a+55a+5, a0, 二次函数 yax2+2ax+2a+5 的对称轴为直线 x1, 当2x1 时,y
19、的最小值为 5a+55, a2, 故选:C 二二.填空题(本大题共填空题(本大题共 4 个小题,每小题个小题,每小题 3 分,共分,共 12 分)分) 11 (3 分)不等式 12x4 的负整数解是 1 【分析】求出不等式的解集,根据不等式的解集求出即可 【解答】解:12x4, 2x3, x, 不等式 12x4 的负整数解是1, 故答案为:1 12(3 分) 某正多边形外接圆的半径为 4, 边心距为 2, 则该正多边形的边长为 4 【分析】首先利用勾股定理求得边长的一半,然后求得边长即可 【解答】解:正多边形外接圆的半径为 4,边心距为 2, 正多边形的边长的一半为:2, 边长为 224, 故


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 陕西省 西安 交大 附中 2020 年中 数学 试卷 答案 解析
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
文档标签
- 西工大附中
- 陕西省西工大附中八年级上语文月考试卷
- 交大附中五模
- 2019陕西数学
- 西安工大附中数学
- 陕西省西安周至县2018八年级下册期中物理
- 2020年交大附中第五次模拟考试
- 陕西省山阳中学
- 2021万维中考黑白卷陕西历史
- 陕西省2020年中考数学试题含答案解析
- 2021年陕西省中考物理三模试卷含答案解析
- 陕西省西安市高新一中2020年中考数学三模试卷含答案解析
- 2019年陕西省西安交大附中中考物理五模试卷含答案解析
- 陕西省西安交大附中分校2020年中考数学二模试卷含答案
- 2020年陕西省西安交大附中中考数学五模试卷含答案解析
- 2018年陕西省西安工大附中中考数学五模试卷含答案解析
- 2018年陕西省西安工大附中中考数学二模试卷含答案解析
- 陕西省西安交大附中2020年中考数学三模试卷含答案解析
- 陕西省2020年中考语文信息试卷含答案



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-152685.html