1、 第第 13 章全等三角形检测卷章全等三角形检测卷 一选择题（共一选择题（共 12 小题，满分小题，满分 36 分，每小题分，每小题 3 分）分） 1下列语句是命题的是（ ） A延长线段 AB B你吃过午饭了吗 C连接 A，B 两点 D直角都相等 2小明同学有一块玻璃的三角板，不小心掉到地上碎成了三块，现要去文具店买一块同样 的三角板，最省事的是（ ） A带去 B带去 C带去 D三块都带去 3下列命题中，假命题是（ ） A斜边及一锐角对应相等的两个直角三角形全等 B一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等 C两个锐角对应相等的两个直角三角形全等 D两条直角边对应相等的两个直
2、角三角形全等 4已知ABCA1B1C1，A 和 A1对应，B 和 B1对应，A70，B150，则C 的度数为（ ） A70 B50 C120 D60 5如图，已知 AEAC，CE，下列条件中，无法判定ABCADE 的是（ ） ABD BBCDE C12 DABAD 6如图，ABCDEF，BC7，EC4，则 CF 的长为（ ） A2 B3 C5 D7 7如图，在 RtABC 中，B90，分别以点 A 和点 C 为圆心，大于AC 的长为半径 画弧，两弧相交于点 E，点 F，作直线 EF 交 BC 于点 D，连接 AD，若 AB3，BC5， 则ABD 的周长为（ ） A5 B6 C7 D8 8有甲、
3、乙、丙三人，甲说乙在说谎，乙说丙在说谎，丙说甲和乙都在说谎，则（ ） A甲说实话，乙和丙说谎 B乙说实话，甲和丙说谎 C丙说实话，甲和乙说谎 D甲、乙、丙都说谎 9如图，点 P 是AOB 的角平分线上一点，过点 P 作 PCOA 于点 C，且 PC3，则点 P 到 OB 的距离为（ ） A3 B4 C5 D6 10等腰三角形的周长为 12cm，其中一边长为 5cm，则该等腰三角形的底边为（ ） A5cm B3cm C3.5cm 或 2cm D8cm 11如图所示，点 E 在 AC 上，ABAD，BCDC，则图中全等的三角形有（ ） A1 对 B2 对 C3 对 D4 对 12已知：如图，在AB
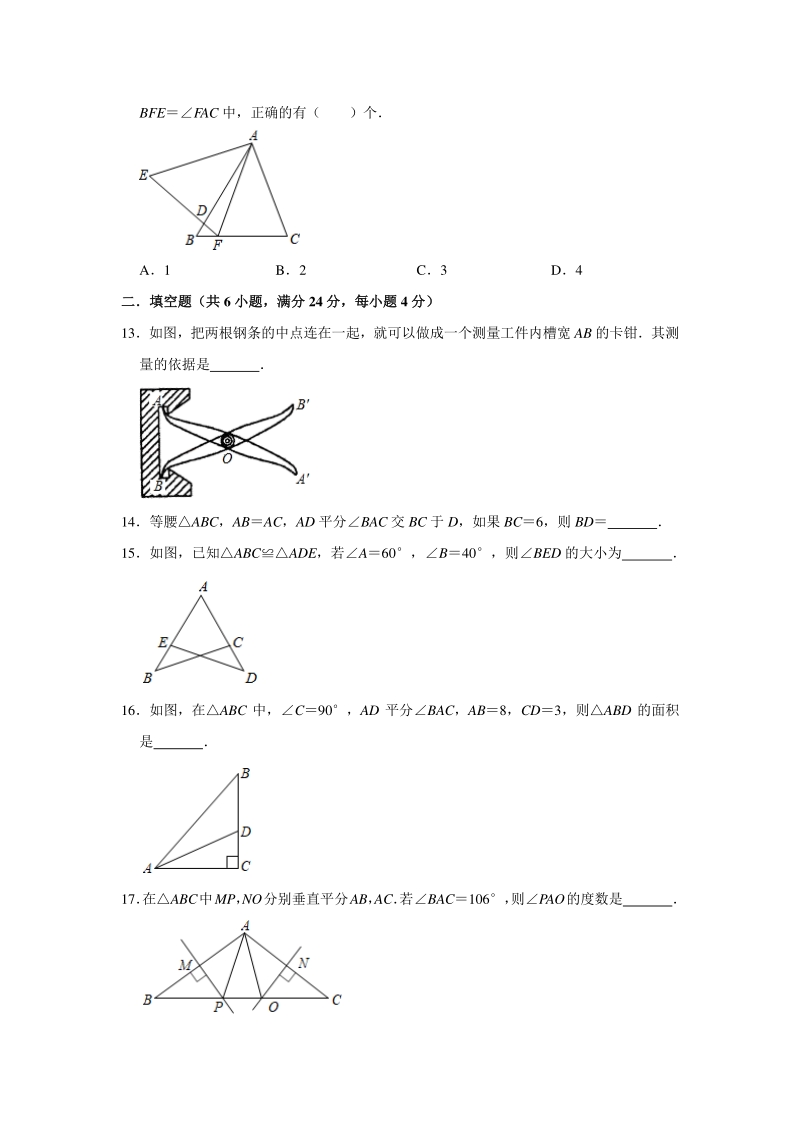
4、C 与AEF 中，点 F 在 BC 上，ABAE，BCEF，BE， AB 交 EF 于点 D下列结论：EABFAC；AFAC；FA 平分EFC； BFEFAC 中，正确的有（ ）个 A1 B2 C3 D4 二填空题（共二填空题（共 6 小题，满分小题，满分 24 分，每小题分，每小题 4 分）分） 13如图，把两根钢条的中点连在一起，就可以做成一个测量工件内槽宽 AB 的卡钳其测 量的依据是 14等腰ABC，ABAC，AD 平分BAC 交 BC 于 D，如果 BC6，则 BD 15如图，已知ABCADE，若A60，B40，则BED 的大小为 16如图，在ABC 中，C90，AD 平分BAC，A
5、B8，CD3，则ABD 的面积 是 17 在ABC中MP， NO分别垂直平分AB， AC 若BAC106， 则PAO的度数是 18如图，点 C 在线段 BD 上，ABBD 于 B，EDBD 于 DACE90，且 AC5cm， CE6cm，点 P 以 2cm/s 的速度沿 ACE 向终点 E 运动，同时点 Q 以 3cm/s 的速度从 E 开始，在线段 EC 上往返运动（即沿 ECEC运动） ，当点 P 到达终点时，P， Q 同时停止运动过 P，Q 分别作 BD 的垂线，垂足为 M，N设运动时间为 ts，当以 P， C，M 为顶点的三角形与QCN 全等时，t 的值为 三解答题（共三解答题（共 8
6、 小题，满分小题，满分 60 分）分） 19 （6 分）已知，如图，ABAE，ABDE，ECB70，D110，求证：ABC EAD 20 （6 分）如图，A、B 表示两个仓库，要在 A、B 一侧的河岸边建造一个码头，使它到两 个仓库的距离相等，码头应建造在什么位置？ 21 （7 分）如图，已知AOB，点 P 是 OA 边上的一点 （1）在 OA 的右侧作APCAOB（用尺规作图法，保留作图痕迹，不写作法） ； （2）在（1）的条件下，判断直线 PC 与直线 OB 的位置关系，并说明理由 22 （7 分）如图，在ABC 中，BADC，BE 平分ABC （1）求证：AEAF； （2）若 ACBC，
7、C32，求AEF 的度数 23（8 分） 已知 OM 是AOB 的平分线， 点 P 是射线 OM 上一点， 点 C、 D 分别在射线 OA、 OB 上，连接 PC、PD （1）如图，当 PCOA，PDOB 时，则 PC 与 PD 的数量关系是 （2） 如图， 点 C、 D 在射线 OA、 OB 上滑动， 且AOB90， OCP+ODP180， 当 PCPD 时，PC 与 PD 在（1）中的数量关系还成立吗？说明理由 24 （8 分）如图，在ABC 和ABD 中，BACABD90，点 E 为 AD 边上的一点， 且 ACAE，连接 CE 交 AB 于点 G，过点 A 作 AFAD 交 CE 于点
8、 F （1）求证：AGEAFC； （2）若 ABAC，求证：ADAF+BD 25 （8 分）如图，在ABC 中，ABAC2，BC50，点 D 在线段 BC 上运动（点 D 不与 B、C 重合） ，连结 AD，作ADE50，DE 交线段 AC 于点 E （1）若 DC2，求证：ABDDCE； （2） 在点 D 的运动过程中， ADE 的形状可以是等腰三角形吗？若可以， 请求出BDA 的度数；若不可以，请说明理由 26 （10 分）如图，已知在ABC 中，ABAC，BC12 厘米，点 D 为 AB 上一点且 BD8 厘米， 点 P 在线段 BC 上以 2 厘米/秒的速度由 B 点向 C 点运动，
9、设运动时间为 t， 同时， 点 Q 在线段 CA 上由 C 点向 A 点运动 （1）用含 t 的式子表示 PC 的长为 ； （2）若点 Q 的运动速度与点 P 的运动速度相等，当 t2 时，三角形 BPD 与三角形 CQP 是否全等，请说明理由； （3）若点 Q 的运动速度与点 P 的运动速度不相等，请求出点 Q 的运动速度是多少时， 能够使三角形 BPD 与三角形 CQP 全等？ 参考答案参考答案 一选择题（共一选择题（共 12 小题，满分小题，满分 36 分，每小题分，每小题 3 分）分） 1解：A、延长线段 AB，没有作出判断，不是命题； B、你吃过午饭了吗，没有作出判断，不是命题； C
10、、连接 A，B 两点，没有作出判断，不是命题； D、直角都相等，是命题； 故选：D 2解：带去符合“角边角”可以配一块同样大小的三角板 故选：C 3解：A、斜边及一锐角对应相等的两个直角三角形利用 AAS 可得全等，是真命题； B、 一条直角边和另一条直角边上的中线对应相等， 可得另一直角边也相等， 构成了 SAS， 能判定全等，是真命题； C、两直角三角形隐含一个条件是两直角相等，两个锐角对应相等，因此构成了 AAA，不 能判定全等，原命题是假命题； D、两条直角边对应相等，构成了 SAS，能判定全等；是真命题； 故选：C 4解：ABCA1B1C1，A 和 A1对应，B 和 B1对应，A70
11、，B150， BB150， 则C 的度数为：180507060 故选：D 5解：A、添加BD，由“AAS”可证ABCADE，故选项 A 不合题意； B、添加 BCDE，由“SAS”可证ABCADE，故选项 B 不合题意； C、添加12，由“ASA”可证ABCADE，故选项 C 不合题意； D、添加 ABAD，不能证明ABCADE，故选项 D 符合题意； 故选：D 6解：ABCDEF， EFBC7， EC4， CF3， 故选：B 7解：根据作图过程可知： EF 是 AC 的垂直平分线， CDAD， ABD 的周长为：AD+BD+ABCD+BD+ABBC+AB5+38 故选：D 8解：A、若甲说的
12、是实话，即乙说的是谎话，则丙没有说谎，即甲、乙都说谎是对的， 与甲说的是实话相矛盾，故 A 不合题意； B、若乙说的是实话，即丙说的谎话，即甲、乙都说谎是错了，即甲，乙至少有一个说了 实话，与乙说的是实话不矛盾，故 B 符合题意； C、若丙说的是实话，甲、乙都说谎是对的，那甲说的乙在说谎是对的，与丙说的是实话 相矛盾，故 C 不合题意； D、若甲、乙、丙都说谎，与丙说的甲和乙都在说谎，相矛盾，故 D 不合题意； 故选：B 9解：如图，过点 P 作 PDOB 于 D， 点 P 是AOB 的角平分线上一点，PCOA， PCPD3， 即点 P 到 OB 的距离等于 3 故选：A 10解：当 5cm
13、是等腰三角形的底边时，则其腰长是（125）23.5（cm） ，能够组成 三角形； 当 5cm 是等腰三角形的腰时，则其底边是 12522（cm） ，能够组成三角形 故选：C 11解：ABAD，BCDC，AC 为公共边， ABCADC BACDAC，BCADCA， ABEADE， CBECDE 故选：C 12解：在AEF 和ABC 中， ， AEFABC（SAS） ， EAFBAC，AFAC，CEFA， EABFAC，AFCC， EFAAFC， 即 FA 平分EFC 又AFBC+FACAFE+BFE， BFEFAC 故正确 故选：D 二填空题（共二填空题（共 6 小题，满分小题，满分 24 分，
14、每小题分，每小题 4 分）分） 13解：O 是 AA，BB的中点， AOAO，BOBO， 又AOB 与AOB是对顶角， AOBAOB 在AOB 和AOB中， ， AOBAOB（SAS） ， ABAB 故答案为 SAS 14解：ABAC，AD 平分BAC， BDCDBC3， 故答案为：3 15解：ABCADE， DB40， BEDA+D60+40100， 故答案为：100 16解：作 DEAB 于 E，如图， AD 平分BAC，DEAB，DCAC， DEDC3， SABD8312 故答案为 12 17解：BAC106， B+C18010674， MP 是线段 AB 的垂直平分线， PAPB， P
15、ABB， 同理，OACC， PAOBAC（PAB+OAC）BAC（B+C）32， 故答案为：32 18 解： 当点 P 在 AC 上， 点 Q 在 CE 上时， 以 P， C， M 为顶点的三角形与QCN 全等， PCCQ， 52t63t， t1， 当点 P 在 AC 上，点 Q 第一次从点 C 返回时，以 P，C，M 为顶点的三角形与QCN 全等， PCCQ， 52t3t6， t， 当点 P 在 CE 上，点 Q 第一次从 E 点返回时，以 P，C，M 为顶点的三角形与QCN 全等， PCCQ， 2t5183t， t， 综上所述：t 的值为 1 或或 三解答题（共三解答题（共 8 小题，满分
16、小题，满分 60 分）分） 19证明：由ECB70得ACB110 又D110 ACBD ABDE CABE 在ABC 和EAD 中， ， ABCEAD（AAS） 20解：连接 AB，码头应建在线段 AB 的垂直平分线与靠近 A、B 一侧的河岸的交汇点处 如图：点 P 就是码头应建的位置 21解： （1）如图，APC 就是所要求作的角； （2）直线 PC 与直线 OB 的位置关系为：PCOB， 理由如下： 由（1）作图可得：APCAOB， PCOB 22 （1）证明：BE 平分ABC， ABECBE， BADC， ABE+BADCBE+C， AFEABE+BAD，AEBCBE+C， AFEAEB
17、， AEAF； （2）解：C32， CBA+CAB180C148， ACBC， CBACAB74， BE 平分ABC， CBEABC37， AEFC+CBE32+3769 23解： （1）PCPD， 理由：OM 是AOB 的平分线， PCPD（角平分线上点到角两边的距离相等） ， 故答案为：PCPD； （2）证明：过点 P 点作 PEOA 于 E，PFOB 于 F，如图， PECPFD90， OM 是AOB 的平分线， PEPF， AOB90，CPD90， PCE+PDO3609090180， 而PDO+PDF180， PCEPDF， 在PCE 和PDF 中， PCEPDF（AAS） ， PC
18、PD 24证明： （1）CABFAE90， CABFAGFAEFAG，即CAFEAG， ACAE， ACFAEG， 在AGE 和AFC 中， ， AGEAFC（ASA） ； （2）延长 AF 至点 H，使 AHAD， 在CAH 和BAD 中， ， CAHBAD（SAS） CHBD，ACHABD90， CHAB， CHAHAG， AGEAFC， AGEAFC， AGFAFG， HCFHFC， HCHF， AHAF+HFAF+CH， ADAF+BD 25 （1）证明：ABAC2，DC2， ABDC， BC50，ADE50， BDA+CDE130， CED+CDE130， BDACED， ABDDC
19、E（AAS） （2）解：可以有以下三种可能： 由（1）得：ABDDCE，得 ADDE 则有DAEDEA65 BDACED65+50115； 由（1）得BDACED 点 D 在线段 BC 上运动（点 D 不与 B、C 重合） ADAE； 当 EAED 时，EADADE50 BDACED50+50100 26解： （1）BP2t，则 PCBCBP122t； 故答案为（122t）cm （2）当 t2 时，BPCQ224 厘米， BD8 厘米 又PCBCBP，BC12 厘米， PC1248 厘米， PCBD， 又ABAC， BC， 在BPD 和CQP 中， BPDCQP（SAS） ； vPvQ， BPCQ， 又BPDCPQ，BC， BPPC6cm，CQBD8cm， 点 P，点 Q 运动的时间 t3 秒， VQ厘米/秒 即点 Q 的运动速度是厘米/秒时，能够使三角形 BPD 与三角形 CQP 全等
