1、 第第 3 章圆的基本性质章末检测卷章圆的基本性质章末检测卷 满分 120 分 姓名：_班级：_学号：_ 一选择题（共一选择题（共 12 小题，满分小题，满分 36 分，每小题分，每小题 3 分）分） 1在平面直角坐标系中，圆心为坐标原点，O 的半径为 10，则 P（10，1）与O 的位 置关系为（ ） A点 P 在O 上 B点 P 在O 外 C点 P 在O 内 D无法确定 2下列叙述中不正确的是（ ） A圆是中心对称图形，圆心是它的对称中心 B圆是轴对称图形，直径是它的对称轴 C连接圆上两点的线段叫弦 D圆上两点间的部分叫弧 3如图，四边形 ABCD 内接于O，AB 为直径，BCCD，连接
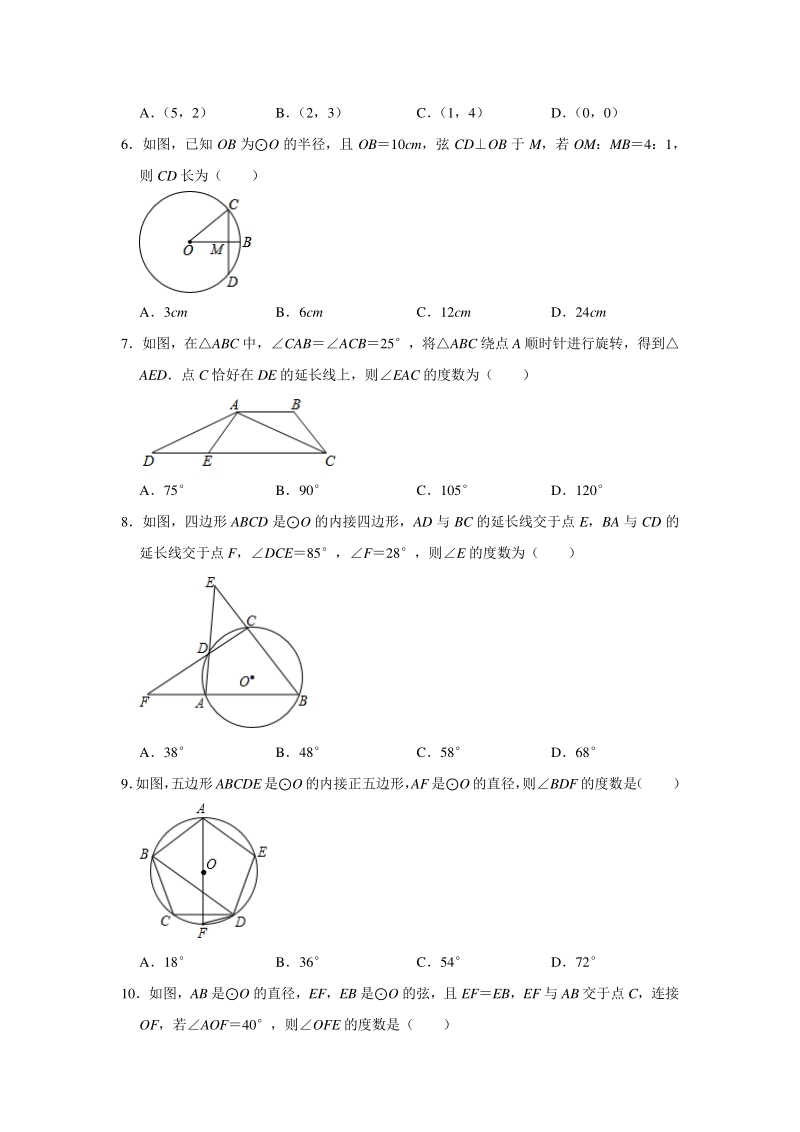
2、AC若DAB50，则 B 的度数为（ ） A50 B65 C75 D130 4如图，ABC 的外接圆O 的半径是 1若C45，则 AB 的长为（ ） A B C2 D2 5如图，ABC 外接圆的圆心坐标是（ ） A （5，2） B （2，3） C （1，4） D （0，0） 6如图，已知 OB 为O 的半径，且 OB10cm，弦 CDOB 于 M，若 OM：MB4：1， 则 CD 长为（ ） A3cm B6cm C12cm D24cm 7如图，在ABC 中，CABACB25，将ABC 绕点 A 顺时针进行旋转，得到 AED点 C 恰好在 DE 的延长线上，则EAC 的度数为（ ） A75 B9
3、0 C105 D120 8如图，四边形 ABCD 是O 的内接四边形，AD 与 BC 的延长线交于点 E，BA 与 CD 的 延长线交于点 F，DCE85，F28，则E 的度数为（ ） A38 B48 C58 D68 9 如图， 五边形ABCDE是O 的内接正五边形， AF是O的直径， 则BDF 的度数是 （ ） A18 B36 C54 D72 10如图，AB 是O 的直径，EF，EB 是O 的弦，且 EFEB，EF 与 AB 交于点 C，连接 OF，若AOF40，则OFE 的度数是（ ） A30 B20 C40 D35 11如图，菱形 ACBD 中，AB 与 CD 交于 O 点，ACB120
4、，以 C 为圆心 AC 为半径作 弧 AB，再以 C 为圆心，CO 为半径作弧 EF 分别交 AC 于 F 点，BC 于 E 点，若 CB2， 则图中阴影部分的面积为（ ） A B C D 12如图，已知正方形 ABCD 的边长为 1，将DCB 绕点 D 顺时针旋转 45得到DGH， HG 交 AB 于点 E，连接 DE 交 AC 于点 F，连接 FG下列结论中正确的有（ ） 四边形 AEGF 是菱形；AEDGED；DFG112.5；BC+FG1.5 A1 个 B2 个 C3 个 D4 个 二填空题（共二填空题（共 6 小题，满分小题，满分 24 分，每小题分，每小题 4 分）分） 13已知一
5、个扇形的面积为 12cm2，圆心角的度数为 108，则它的弧长为 14O 的圆心是原点 O（0，0） ，半径为 5，点 A（3，a）在O 上，如果点 A 在第一象 限内，那么 a 15如图，在平面直角坐标系中，将点 P（4，6）绕坐标原点 O 顺时针旋转 90得到点 Q， 则点 Q 的坐标为 16 如图， 将ABC 绕点 A 顺时针旋转得到ABC， 点 C恰好落在线段 AB 上， 连接 BB 若 AC1，AB3，则 BC 17如图，AB 为O 直径，点 C、D 在O 上，已知BOC70，ADOC，则AOD 度 18如图，AB 是O 的直径，C 是O 上一点，ACB 的平分线交O 于 D，且 A
6、B10， 则 AD 的长为 三解答题（共三解答题（共 7 小题，满分小题，满分 60 分）分） 19 （8 分）如图，点 A，C，D，B 在以 O 点为圆心，OA 长为半径的圆弧上，ACCD DB，AB 交 OC 于点 E求证：AECD 20 （8 分）如图，在一座圆弧形拱桥，它的跨度 AB 为 60m，拱高 PM 为 18m，当洪水泛滥 到跨度只有 30m 时，就要采取紧急措施，若某次洪水中，拱顶离水面只有 4m，即 PN 4m 时，试通过计算说明是否需要采取紧急措施 21 （8 分）如图，AB 是O 的直径，CD 是O 的弦，如果ACD30 （1）求BAD 的度数； （2）若 AD，求 D
7、B 的长 22 （8 分）如图， 在平面直角坐标系中， 已知ABC 的三个顶点的坐标分别为 A（3，5） 、 B（2，1） 、C（1，3） （1）画出将ABC 绕点 O 顺时针旋转 90后所得到的图形A1B1C1；并写出 A1，B1， C1的坐标 （2）计算出边 BC 扫过的面积 23 （8 分）如图，在ABC 中，ACBC，D 是 AB 上一点，O 经过点 A、C、D，交 BC 于点 E，过点 D 作 DFBC，交O 于点 F 求证： （1）四边形 DBCF 是平行四边形； （2）AFEF 24 （10 分）取一副三角板按如图所示拼接，固定三角板 ADC，将三角板 ABC 绕点 A 顺时 针
8、方向旋转，旋转角度为 （045） ，得到ABC 当 为多少度时，ABDC？ 当旋转到图所示位置时， 为多少度？ 连接 BD，当 045时，DBC+CAC+BDC 值是否会发生变化？为什 么？ 25 （10 分）如图，将O 内的一条弦 AB 绕点 A 按顺时针方向旋转得到弦 AC，过点 B 作 弦 BD，与 AC 相交于点 M，且BACCADACBACD （1）求证：ACBD； （2）作ACD 关于直线 AD 对称的AED（E 与 C 是对应点） 若 CD5，DM3，求 点 O 到弦 AD 的距离 参考答案参考答案 一选择题（共一选择题（共 12 小题，满分小题，满分 36 分，每小题分，每小题
9、 3 分）分） 1解：圆心 P 的坐标为（10，1） ， OP O 的半径为 10， 10， 点 P 在O 外 故选：B 2解：A、圆是中心对称图形，圆心是它的对称中心，正确； B、圆是轴对称图形，直径所在的直线为圆的对称轴，错误； C、连接圆上两点的线段叫弦，正确； D、圆上两点间的部分叫弧，正确； 故选：B 3解：BCCD， ， DACCAB， DAB50， CAB5025， AB 是直径， ACB90， B902565， 故选：B 4解：连接 OA，OB， C45， AOB90， OAOB1， ABOB， 故选：A 5解：作线段 BC 的垂直平分线，作 AB 的垂直平分线， 两条直线相交
10、于点 D， 所以 D 的坐标为（5，2） 故选：A 6解：弦 CDOB 于 M， CMDMCD， OM：MB4：1， OMOB8cm， CM6（cm） ， CD2CM12cm， 故选：C 7解：将ABC 绕点 A 顺时针进行旋转，得到AED， ABCAED， ADAC，BACEAD25，ADEACB25， ADEACD25， DAC1802525130， EACDACDAE13025105， 故选：C 8解：BDCEF57， 四边形 ABCD 是O 的内接四边形， EDCB57， E180DCEEDC38， 故选：A 9解：AF 是O 的直径，五边形 ABCDE 是O 的内接正五边形， ，BA
11、E108， ， BAFBAE54， BDFBAF54， 故选：C 10解：如图，连接 BF，OE EFEB，OEOE，OFOB， OEFOEB（SSS） ， OFEOBE， OEOB0F， OEFOFEOEBOBE，OFBOBF， ABFAOF20， OFBOBE20， OFB+OBF+OFE+OBE+BEF180， 4EFO+40180， OFE35， 故选：D 11解：四边形 ACBD 是菱形，ACB120， DCAACB60，ABCD，ADBCAC2， CBACBA（180ACB）30，AOC90， OCAC1， 由勾股定理得：AO， ACAD，ACD60， ACD 是等边三角形， CD
12、AC2， DOCDOC211， 阴影部分的面积 SS扇形DCASDOA， 故选：A 12证明：四边形 ABCD 是正方形， ADDCBCAB，DABADCDCBABC90，ADBBDC CADCAB45， DHG 是由DBC 旋转得到， DGDCAD，DGEDCBDAE90， 在 RtADE 和 RtGDE 中， ， AEDGED（HL） ，故正确， ADEEDG22.5，AEEG， AEDAFE67.5， AEAF，同理AEFGEF，可得 EGGF， AEEGGFFA， 四边形 AEGF 是菱形，故正确， DFGGFC+DFCBAC+DAC+ADF112.5，故正确 AEFGEGBG，BEA
13、E， BEAE， AE， CB+FG1.5，故错误 故选：C 二填空题（共二填空题（共 6 小题，满分小题，满分 24 分，每小题分，每小题 4 分）分） 13解：设扇形的半径为 Rcm， 扇形的面积为 12cm2，圆心角的度数为 108， 12， 解得：R2， 弧长为（cm） ， 故答案为：cm 14解：O 的圆心是原点 O（0，0） ，半径为 5，点 A（3，a）在O 上， |a|4， 点 A 在第一象限内， a4 故答案为：4 15解：作图如下， MPO+POM90，QON+POM90， MPOQON， 在PMO 和ONQ 中， ， PMOONQ（AAS） ， PMON，OMQN， P
14、点坐标为（4，6） ， Q 点坐标为（6，4） ， 故答案为（6，4） 16解：ABC 绕点 A 顺时针旋转得到ABC，点 C恰好落在线段 AB 上， ACAC1， BCABAC312 故答案为 2 17解：ADOC， BOCDAO70， 又ODOA， ADODAO70， AOD180707040 18解：AB 是O 的直径， ADB90， ACB 的平分线交O 于 D， ACDBCD， ， ADBD， ABD 为等腰直角三角形， ADAB105 故答案为 5 三解答题（共三解答题（共 7 小题，满分小题，满分 60 分）分） 19证明：方法一：连接 OD， ACCDDB，弧 AC弧 CD弧
15、DB， AOCCODBOD， COBCOD+DOB2COD2AOC， COB2CAE，AOCCAE， 在AOC 中，OAOC， 在ACE 中，AEC180CAEACE ， ACEAEC，ACAE， ACCD，AECD 方法二：连接 OD， ACCDDB，弧 AC弧 CD弧 DB， AOCCODBOD， COBCOD+DOB2COD2AOC， COB2CAE，AOCCAE， CAOCAE+EAO，AECAOC+EAO， CAOAEC， 在AOC 中，OAOC， ACOCAO， ACOAEC，ACAE， ACCD，AECD； 方法三：连接 AD，OD， ACDB，弧 AC弧 BD， ADCDAB，
16、 CDAB， AECDCO， ACCD，AODO， COAD， ACODCO， ACOAEC，ACAE， ACCD，AECD 20解：设圆弧所在圆的圆心为 O，连接 OA、OA，设半径为 x 米， 则 OAOAOP， 由垂径定理可知 AMBM，ANBN， AB60 米， AM30 米，且 OMOPPM（x18）米， 在 RtAOM 中，由勾股定理可得 AO2OM2+AM2， 即 x2（x18）2+302，解得 x34， ONOPPN34430（米） ， 在 RtAON 中，由勾股定理可得 AN16（米） ， AB32 米30 米， 不需要采取紧急措施 21解： （1）AB 是O 的直径， AD
17、B90， BACD30， BAD90B903060； （2）在 RtADB 中，BDAD3 22解： （1）如图A1B1C1即为所求A1（5，3）B1（1，2）C1（3，1） （2）边 BC 扫过的面积 23证明： （1）ACBC， BACB， DFBC， ADFB， BACCFD， ADFCFD， BDCF， DFBC， 四边形 DBCF 是平行四边形； （2）连接 AE， ADFB，ADFAEF， AEFB， 四边形 AECF 是O 的内接四边形， ECF+EAF180， BDCF， ECF+B180， EAFB， AEFEAF， AFEF 24解：ABCD， CABACD30， CAC1
18、5 当旋转到图所示位置时， CAB45， CAB45； 不变， 理由如下： 如图， EHCBDC+DBC，CECCAC+C， DBC+CAC+BDCEHC+CECC， EHC+CEC+C180， EHC+CEC18045135， DBC+CAC+BDC135C105 25 （1）证明：BACCADACBACD， BAC+ACDACB+CAD， ACDABD，CADCBD， BAC+ABDACB+CBD， BAC+ABD+ACB+CBD180， BAC+ABD90， AMB90， ACBD； （2）将弦 AB 绕点 A 按顺时针方向旋转得到弦 AC， ABAC， ABCACBADB， ACD 与AED 关于直线 AD 对称， ACAEAB，ADCADE， ABC+ADCADB+ADE180， B，D，E 三点共线， 作 OHAD 于 H，作O 的直径 DF，连接 AF，则 AHDH，FAD90， F+ADF90， FABD，ABD+BAC90， ADFBAC， ， AFBC， CD5，DM3， EMED+DMCD+DM8， ABAE，ACBD， BMEM8，CM4， BC4， AF4， AHDH，ODOF， OHAF2， 即点 O 到弦 AD 的距离为 2
