1、 第 1 页（共 24 页） 2020 年广东省东莞市莞城区二校联考中考数学二模试卷年广东省东莞市莞城区二校联考中考数学二模试卷 一选择题（共一选择题（共 10 小题）小题） 12020 的相反数是（ ） A2020 B2020 C D 2据统计，2019 年十一期间，湖州市共接待国内外游客约 585 万人次，数据 585 万用科学 记数法表示为（ ） A5.85105 B5.85106 C0.585107 D585106 3如图，该几何体的左视图是（ ） A B C D 4一个同学周一到周五的体温测得的情况是 36.2 度，36.2 度，36.5 度，36.3 度，36.4 度， 则这五个度
2、数的众数和中位数分别是（ ） A36.3，36.2 B36.2，36.3 C36.2，36.4 D36.2，36.5 5不等式 x223x 的解集是（ ） Ax1 Bx1 Cx Dx 6下列图形中，是中心对称图形但不是轴对称图形的是（ ） A B C D 7下列各式计算结果是 a6的是（ ） 第 2 页（共 24 页） Aa3+a3 Ba12a2 Ca2a3 D （a3）2 8关于 x 的一元二次方程 x22x+m0 有实数根，则实数 m 的取值范围是（ ） Am1 Bm1 Cm1 Dm1 9如图，已知 ab，点 A 在直线 a 上，点 B，C 在直线 b 上，若1125，250， 则3 为（
3、 ） A55 B65 C70 D75 10如图，正方形 ABCD 中，点 E 是 AD 边的中点，BD，CE 交于点 H，BE、AH 交于点 G， 则下列结论： ABEDCE； AGBE； SBHESCHD； AHBEHD其中正确的是（ ） A B C D 二填空题（共二填空题（共 7 小题）小题） 11因式分解 3xy6y 12若一个正 n 边形的一个外角为 36，则 n 等于 13若实数 a，b 满足，则（ab）2020的值为 14如果 mn3，那么 2m2n3 的值是 15从，0，3 这五个数中随机抽取一个数，恰好是无理数的概率是 16如图，扇形 ABC 的圆心角为 120，半径为 8，
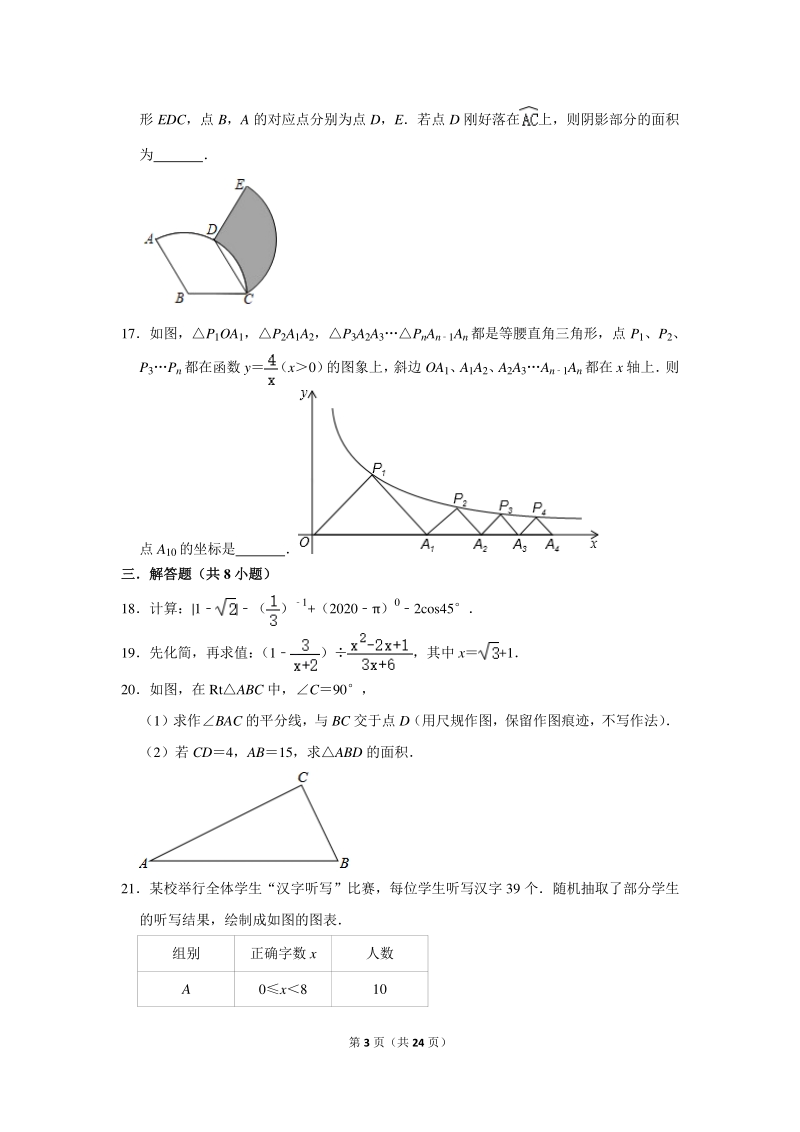
4、将扇形 ABC 绕点 C 顺时针旋转得到扇 第 3 页（共 24 页） 形 EDC，点 B，A 的对应点分别为点 D，E若点 D 刚好落在上，则阴影部分的面积 为 17如图，P1OA1，P2A1A2，P3A2A3PnAn1An都是等腰直角三角形，点 P1、P2、 P3Pn都在函数 y （x0） 的图象上， 斜边 OA1、 A1A2、 A2A3An1An都在 x 轴上 则 点 A10的坐标是 三解答题（共三解答题（共 8 小题）小题） 18计算：|1|（） 1+（2020）02cos45 19先化简，再求值： （1），其中 x+1 20如图，在 RtABC 中，C90， （1）求作BAC 的平分
5、线，与 BC 交于点 D（用尺规作图，保留作图痕迹，不写作法） （2）若 CD4，AB15，求ABD 的面积 21某校举行全体学生“汉字听写”比赛，每位学生听写汉字 39 个随机抽取了部分学生 的听写结果，绘制成如图的图表 组别 正确字数 x 人数 A 0 x8 10 第 4 页（共 24 页） B 8x16 15 C 16x24 25 D 24x32 m E 32x40 n 根据以上信息完成下列问题： （1）统计表中的 m ，n ，并补全条形统计图； （2）扇形统计图中“C 组”所对应的圆心角的度数是 ； （3）已知该校共有 900 名学生，如果听写正确的字的个数少于 24 个定为不合格，请
6、你 估计该校本次听写比赛不合格的学生人数 22 在我市雨污分流工程中， 甲、 乙两个工程队共同承担茅洲河某段 720 米河道的清淤任务， 已知甲队每天能完成的长度是乙队每天能完成长度的 2 倍，且甲工程队清理 300 米河道 所用的时间比乙工程队清理 200 米河道所用的时间少 5 天 （1）甲、乙两工程队每天各能完成多少米的清淤任务； （2）若甲队每天清淤费用为 2 万元，乙队每天清淤费用为 0.8 万元，要使这次清淤的总 费用不超过 60 万元，则至少应安排乙工程队清淤多少天？ 23 如图， 矩形 ADCD 中， AB10， BC7， P 为 AD 上一点， 将ADP 沿 BP 翻折至EB
7、P， PE 与 CD 交于点 O，且 OEOD （1）求证：OPOF； （2）求 AP 的长 第 5 页（共 24 页） 24如图 1，BC 是O 的直径，点 A 在O 上，点 D 在 CA 的延长线上，DEBC，垂足为 点 E，DE 与O 相交于点 H，与 AB 相交于点 I过点 A 作DAFABO，与 DE 相交 于点 F （1）求证：AF 为O 的切线； （2）当 ABAD，且 tanDAF时，求：的值； （3）如图 2，在（2）的条件下，延长 FA，BC 相交于点 G，若 CG10，求线段 EH 的 长 25 如图， 直线 yx2 与 x 轴交于点 B， 与 y 轴交于点 A， 抛物线
8、 yax2x+c 经过 A， B 两点，与 x 轴的另一交点为 C （1）求抛物线的解析式； （2）M 为抛物线上一点，直线 AM 与 x 轴交于点 N，当时，求点 M 的坐标； （3）P 为抛物线上的动点，连接 AP，当PAB 与AOB 的一个内角相等时，直接写出 点 P 的坐标 第 6 页（共 24 页） 第 7 页（共 24 页） 2020 年广东省东莞市莞城区二校联考中考数学二模试卷年广东省东莞市莞城区二校联考中考数学二模试卷 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 10 小题）小题） 12020 的相反数是（ ） A2020 B2020 C D 【分析】直接利
9、用相反数的定义得出答案 【解答】解：2020 的相反数是：2020 故选：B 2据统计，2019 年十一期间，湖州市共接待国内外游客约 585 万人次，数据 585 万用科学 记数法表示为（ ） A5.85105 B5.85106 C0.585107 D585106 【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相 同当原数绝对值1 时，n 是正数；当原数的绝对值1 时，n 是负数 【解答】解：585 万58500005.85106， 故选：B 3如图，该几何体的左视图是
10、（ ） A B C D 【分析】根据左视图是从物体左面看所得到的图形即可解答 【解答】解：根据左视图的概念可知，从物体的左面看得到的视图是 D 故选：D 4一个同学周一到周五的体温测得的情况是 36.2 度，36.2 度，36.5 度，36.3 度，36.4 度， 则这五个度数的众数和中位数分别是（ ） 第 8 页（共 24 页） A36.3，36.2 B36.2，36.3 C36.2，36.4 D36.2，36.5 【分析】将这 5 个数据从小到大重新排列，再根据众数和中位数的概念求解可得 【解答】解：将这 5 个数据重新排列为 36.2、36.2、36.3、36.4、36.5， 则这组数据
11、的众数为 36.2，中位数为 36.3， 故选：B 5不等式 x223x 的解集是（ ） Ax1 Bx1 Cx Dx 【分析】根据解一元一次不等式基本步骤：移项、合并同类项、系数化为 1 可得 【解答】解：x223x， x+3x2+2， 4x4， 则 x1， 故选：A 6下列图形中，是中心对称图形但不是轴对称图形的是（ ） A B C D 【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解 【解答】解：A、是轴对称图形但不是中心对称图形，故本选项不合题意； B、是轴对称图形但不是中心对称图形，故本选项不合题意； C、是中心对称图形但不是轴对称图形，故本选项符合题意； D、既是轴
12、对称图形也是中心对称图形，故本选项不合题意 故选：C 7下列各式计算结果是 a6的是（ ） Aa3+a3 Ba12a2 Ca2a3 D （a3）2 【分析】根据幂的乘方、同底数幂的乘法和除法的运算法则以及合并同类项计算后利用 第 9 页（共 24 页） 排除法求解 【解答】解：A、a3+a32a3，结果不符合； B、a12a2a10，结果不符合； C、a2a3a5，结果不符合； D、 （a3）2a6，结果符合； 故选：D 8关于 x 的一元二次方程 x22x+m0 有实数根，则实数 m 的取值范围是（ ） Am1 Bm1 Cm1 Dm1 【分析】根据判别式的意义得到（2）24m0，然后解不等式
13、即可 【解答】解：根据题意得（2）24m0， 解得 m1 故选：A 9如图，已知 ab，点 A 在直线 a 上，点 B，C 在直线 b 上，若1125，250， 则3 为（ ） A55 B65 C70 D75 【分析】利用平行线的性质结合三角形的外角的性质解决问题即可 【解答】解：ab，1125， ACD125， 250， 31255075 故选：D 10如图，正方形 ABCD 中，点 E 是 AD 边的中点，BD，CE 交于点 H，BE、AH 交于点 G， 则下列结论： ABEDCE； AGBE； 第 10 页（共 24 页） SBHESCHD； AHBEHD其中正确的是（ ） A B C
14、D 【分析】根据正方形的性质证得BAECDE，推出ABEDCE，可知正确； 利用正方形性质证ADHCDH，求得HADHCD，推出ABEHAD；求出 ABE+BAG90；最后在AGE 中根据三角形的内角和是 180求得AGE90 即可得到正确根据 ADBC，求出 SBDESCDE，推出 SBDESDEHSCDES DEH，即；SBHESCHD，故正确；由AHDCHD，得到邻补角和对顶角相等得 到AHBEHD，故正确； 【解答】解：四边形 ABCD 是正方形，E 是 AD 边上的中点， AEDE，ABCD，BADCDA90， BAECDE（SAS） ， ABEDCE， 故正确； 四边形 ABCD
15、是正方形， ADDC，ADBCDB45，DHDH， ADHCDH（SAS） ， HADHCD， ABEDCE ABEHAD， BADBAH+DAH90， ABE+BAH90， AGB1809090， AGBE， 故正确； 第 11 页（共 24 页） ADBC， SBDESCDE， SBDESDEHSCDESDEH， 即；SBHESCHD， 故正确； ADHCDH， AHDCHD， AHBCHB， BHCDHE， AHBEHD， 故正确； 故选：B 二填空题（共二填空题（共 7 小题）小题） 11因式分解 3xy6y 3y（x2） 【分析】直接提取公因式进而分解因式即可 【解答】解：3xy6y
16、3y（x2） 故答案为：3y（x2） 12若一个正 n 边形的一个外角为 36，则 n 等于 10 【分析】利用多边形的外角和即可解决问题 【解答】解：n3603610 故答案为 10 13若实数 a，b 满足，则（ab）2020的值为 1 【分析】根据非负数的性质列出算式，求出 a、b 的值，计算即可 【解答】解：由题意得，a20，b+0， 第 12 页（共 24 页） 解得，a2，b， 则（ab）2020（1）20201 故答案为：1 14如果 mn3，那么 2m2n3 的值是 3 【分析】原式前两项提取公因式变形后，把已知等式代入计算即可求出值 【解答】解：mn3， 原式2（mn）3 2
17、33 63 3 故答案为：3 15从，0，3 这五个数中随机抽取一个数，恰好是无理数的概率是 【分析】直接利用概率公式计算得出答案 【解答】 解：从，0， 3 这五个数中随机抽取一个数， 抽到的无理数的有， 这 2 种可能， 抽到的无理数的概率是， 故答案为： 16如图，扇形 ABC 的圆心角为 120，半径为 8，将扇形 ABC 绕点 C 顺时针旋转得到扇 形 EDC，点 B，A 的对应点分别为点 D，E若点 D 刚好落在上，则阴影部分的面积 为 +16 【分析】 证明BCD 是等边三角形， 根据 S阴S扇形DCE （S扇形BDCSBCD） 计算即可 【解答】解：如图，连接 BD 第 13
18、页（共 24 页） 由题意：CDCBBD， BCD 是等边三角形， DBC60， S阴S扇形DCE（S扇形BDCSBCD） （82） +16， 故答案为+16 17如图，P1OA1，P2A1A2，P3A2A3PnAn1An都是等腰直角三角形，点 P1、P2、 P3Pn都在函数 y （x0） 的图象上， 斜边 OA1、 A1A2、 A2A3An1An都在 x 轴上 则 点 A10的坐标是 （4，0） 【分析】由于P1OA1是等腰直角三角形，可知直线 OP1的解析式为 yx，将它与 y 联立，求出方程组的解，得到点 P1的坐标，则 A1的横坐标是 P1的横坐标的两倍，从而 确定点 A1的坐标；由于
19、P1OA1，P2A1A2都是等腰直角三角形，则 A1P2OP1，直线 A1P2可看作是直线OP1向右平移OA1个单位长度得到的， 因而得到直线 A1P2的解析式， 同样，将它与 y联立，求出方程组的解，得到点 P2的坐标，则 P2的横坐标是线段 A1A2的中点，从而确定点 A2的坐标；依此类推，从而确定点 A10的坐标 【解答】解：过 P1作 P1B1x 轴于 B1， 易知 B1（2，0）是 OA1的中点， A1（4，0） 第 14 页（共 24 页） 可得 P1的坐标为（2，2） ， P1O 的解析式为：yx， P1OA1P2，A1P2的表达式一次项系数相等， 将 A1（4，0）代入 yx+
20、b， b4， A1P2的表达式是 yx4， 与 y（x0）联立，解得 P2（2+2，2+2） 仿上，A2（4，0） P3（2+2，2+2） ，A3（4，0） 依此类推，点 An的坐标为（4，0） 故点 A10的坐标是（4，0） 故答案为： （4，0） 三解答题（共三解答题（共 8 小题）小题） 18计算：|1|（） 1+（2020）02cos45 【分析】直接利用绝对值的性质以及负整数指数幂的性质、零指数幂的性质、特殊角的 三角函数值分别化简得出答案 【解答】解：原式13+12 13+1 3 19先化简，再求值： （1），其中 x+1 【分析】根据分式的减法和除法可以化简题目中的式子，然后将
21、x 的值代入化简后的式 子即可解答本题 第 15 页（共 24 页） 【解答】解： （1） ， 当 x+1 时，原式 20如图，在 RtABC 中，C90， （1）求作BAC 的平分线，与 BC 交于点 D（用尺规作图，保留作图痕迹，不写作法） （2）若 CD4，AB15，求ABD 的面积 【分析】 （1）直接利用角平分线的作法得出答案； （2）过点 D 作 DEAB 于点 E，利用角平分线的性质结合三角形面积求法得出答案 【解答】解： （1）如图所示： AD 即为所求； （2）过点 D 作 DEAB 于点 E，如图 2 所示： AD 平分BAC，ACCD DEDC4， ABD 的面积ABDE
22、15430 第 16 页（共 24 页） 21某校举行全体学生“汉字听写”比赛，每位学生听写汉字 39 个随机抽取了部分学生 的听写结果，绘制成如图的图表 组别 正确字数 x 人数 A 0 x8 10 B 8x16 15 C 16x24 25 D 24x32 m E 32x40 n 根据以上信息完成下列问题： （1）统计表中的 m 30 ，n 20 ，并补全条形统计图； （2）扇形统计图中“C 组”所对应的圆心角的度数是 90 ； （3）已知该校共有 900 名学生，如果听写正确的字的个数少于 24 个定为不合格，请你 估计该校本次听写比赛不合格的学生人数 【分析】 （1）根据条形图和扇形图确
23、定 B 组的人数环绕所占的百分比求出样本容量，求 出 m、n 的值； （2）求出 C 组”所占的百分比，得到所对应的圆心角的度数； （3）求出不合格人数所占的百分比，求出该校本次听写比赛不合格的学生人数 【解答】解： （1）从条形图可知，B 组有 15 人， 从扇形图可知，B 组所占的百分比是 15%，D 组所占的百分比是 30%，E 组所占的百分 比是 20%， 1515%100， 10030%30， 第 17 页（共 24 页） 10020%20， m30，n20； （2） “C 组”所对应的圆心角的度数是 2510036090； （3）估计这所学校本次听写比赛不合格的 学生人数为：900
24、（10%+15%+25%） 450 人 22 在我市雨污分流工程中， 甲、 乙两个工程队共同承担茅洲河某段 720 米河道的清淤任务， 已知甲队每天能完成的长度是乙队每天能完成长度的 2 倍，且甲工程队清理 300 米河道 所用的时间比乙工程队清理 200 米河道所用的时间少 5 天 （1）甲、乙两工程队每天各能完成多少米的清淤任务； （2）若甲队每天清淤费用为 2 万元，乙队每天清淤费用为 0.8 万元，要使这次清淤的总 费用不超过 60 万元，则至少应安排乙工程队清淤多少天？ 【分析】 （1）设乙工程队每天能完成 x 米的清淤任务，则甲工程队每天能完成 2x 米的清 淤任务，根据工作时间工
25、作总量工作效率结合甲工程队清理 300 米河道所用的时间 比乙工程队清理 200 米河道所用的时间少 5 天，即可得出关于 x 的分式方程，解之经检 验后即可得出结论； （2）设应安排乙工程队清淤 m 天，则安排甲工程队清淤天，根据总费用每 天清淤费用工作时间结合这次清淤的总费用不超过 60 万元， 即可得出关于 m 的一元一 次不等式，解之取其中的最小值即可得出结论 【解答】解： （1）设乙工程队每天能完成 x 米的清淤任务，则甲工程队每天能完成 2x 米 的清淤任务， 依题意，得：5， 第 18 页（共 24 页） 解得：x10， 经检验，x10 是原方程的解，且符合题意， 2x20 答：
26、甲工程队每天能完成 20 米的清淤任务，乙工程队每天能完成 10 米的清淤任务 （2）设应安排乙工程队清淤 m 天，则安排甲工程队清淤天， 依题意，得：0.8m+260， 解得：m60 答：至少应安排乙工程队清淤 60 天 23 如图， 矩形 ADCD 中， AB10， BC7， P 为 AD 上一点， 将ADP 沿 BP 翻折至EBP， PE 与 CD 交于点 O，且 OEOD （1）求证：OPOF； （2）求 AP 的长 【分析】 （1）由折叠的性质得出EA90，从而得到DE90，然后可证 明ODPOEF，从而得到 OPOF （2）由ODPOEF，得出 OPOF，PDFE，从而得到 DFP
27、E，设 APEPDF x，则 PDEF6x，DFx，求出 CF、BF，根据勾股定理得出方程，解方程即可 【解答】解： （1）四边形 ABCD 是矩形， DAC90，ADBC6，CDAB8， 由翻折的性质可知：EPAP，EA90，BEAB8， 在ODP 和OEF 中， ， ODPOEF（ASA） OPOF 第 19 页（共 24 页） （2）ODPOEF（ASA） ， OPOF，PDEF DFEP 设 APEPDFx，则 PDEF7x，CF10 x，BF10（7x）3+x， 在 RtFCB 根据勾股定理得：BC2+CF2BF2，即 72+（10 x）2（1+2）2， 解得：x， AP 24如图
28、1，BC 是O 的直径，点 A 在O 上，点 D 在 CA 的延长线上，DEBC，垂足为 点 E，DE 与O 相交于点 H，与 AB 相交于点 I过点 A 作DAFABO，与 DE 相交 于点 F （1）求证：AF 为O 的切线； （2）当 ABAD，且 tanDAF时，求：的值； （3）如图 2，在（2）的条件下，延长 FA，BC 相交于点 G，若 CG10，求线段 EH 的 长 【分析】 （1）欲证明 AF 是切线，只要证明 OAAF 即可； （2）首先证明DBDAF，推出 tanBtanD，推出 AD2AI，由 AD AB，推出 BIIA，BE2IE，设 IEa，则 BE2a，BIAIa
29、，推出 ACAB a，在 RtABC 中，BC5a，可得 ECBCBE5a2a3a，由此即可 解决问题； （3）只要证明GACGBA，可得，由 CG10，推出 GA20， 第 20 页（共 24 页） BG40，BC30，由 BC5a30，推出 a6，可得 BE12，EC18，再证明CEH HEB，可得 HE2BEEC，即可解决问题； 【解答】 （1）证明：如图 1 中，连接 OA BC 是直径， BACBAD90， DAF+FAI90， OAOB， OBAOAB， DAFABO， OABDAF， OAB+FAI90， FAO90，即 OAAF， AF 是O 的切线 （2）解：如图 2 中，
30、IEBIAD90，BIEAID， DB， DAFB， 第 21 页（共 24 页） DBDAF， tanBtanD， AD2AI，ADAB， BIIA， BE2IE，设 IEa，则 BE2a，BIAIa， ACABa， 在 RtABC 中，BC5a， ECBCBE5a2a3a， 3 （3）解：如图 21 中，连接 CH、BH GACDAFABG，GG， GACGBA， ， CG10， GA20，BG40，BC30， BC5a30， a6， BE12，EC18， HEBC， HEBEHCBHC90， HBE+BHE90，BHE+CHE90， 第 22 页（共 24 页） CEHEBH， CEHH
31、EB， 可得 HE2BEEC1218， HE6 25 如图， 直线 yx2 与 x 轴交于点 B， 与 y 轴交于点 A， 抛物线 yax2x+c 经过 A， B 两点，与 x 轴的另一交点为 C （1）求抛物线的解析式； （2）M 为抛物线上一点，直线 AM 与 x 轴交于点 N，当时，求点 M 的坐标； （3）P 为抛物线上的动点，连接 AP，当PAB 与AOB 的一个内角相等时，直接写出 点 P 的坐标 【分析】 （1）直线 yx2 与 x 轴交于点 B，与 y 轴交于点 A，则点 A、B 的坐标分别 为： （0，2） 、 （4，0） ，即可求解； （2）直线 MA 的表达式为：y（m）
32、x2，则点 N（，0） ，当时， 则，即：，即可求解； （3）分PABAOB90、PABOAB、PABOBA 三种情况，分别求解即可 【解答】解： （1）直线 yx2 与 x 轴交于点 B，与 y 轴交于点 A，则点 A、B 的坐标 分别为： （0，2） 、 （4，0） ， 则 c2，将点 B 的坐标代入抛物线表达式并解得：a， 故抛物线的表达式为：yx2x2； （2）设点 M（m，m2m2） 、点 A（0，2） ， 第 23 页（共 24 页） 将点 M、A 的坐标代入一次函数表达式：ykx+b 并解得： 直线 MA 的表达式为：y（m）x2， 则点 N（，0） ， 当时，则，即：， 解得：
33、m5 或2 或 2 或 1， 故点 M 的坐标为： （5，3）或（2，3）或（2，3）或（1，3） ； （3）PABAOB90时， 则直线 AP 的表达式为：y2x2， 联立并解得：x1 或 0（舍去 0） ， 故点 P（1，0） ； 当PABOAB 时， 当点 P 在 AB 上方时，无解； 当点 P 在 AB 下方时， 将OAB 沿 AB 折叠得到OAB，直线 OA 交 x 轴于点 H、交抛物线为点 P，点 P 为所 求， 则 BOOB4，OAOA2，设 OHx， 第 24 页（共 24 页） 则 sinH，即：，解得：x，则点 H（，0） ， 则直线 AH 的表达式为：yx2， 联立并解得：x，故点 P（，） ； 当PABOBA 时， 当点 P 在 AB 上方时， 则 AHBH， 设 OHa，则 AHBH4a，AO2， 故（4a）2a2+4，解得：a， 故点 H（，0） ， 则直线 AH 的表达式为：yx2， 联立并解得：x0 或（舍去 0） ， 故点 P（，） ； 当点 P 在 AB 下方时， 同理可得：点 P（3，2） ； 综上，点 P 的坐标为： （1，0）或（，）或（，）或（3，2）
