1、第 22 课时 三角形全等(60 分)一、选择题(每题 5 分，共 20 分)12016宜昌 如图 221，在方格纸中，以 AB 为一边作ABP，使之与ABC 全等，从 P1，P 2，P 3，P 4 四个点中找出符合条件的点 P，则点 P 有 (C)A1 个 B2 个 C3 个 D4 个【解析】 要使ABP 与 ABC 全等，点 P 到 AB 的距离应该等于点 C 到AB 的距离，即 3 个单位长度，故点 P 的位置可以是 P1，P 3，P 4 三个图 221 图 2222如图 222，下列条件中，不能证明ABDACD 的是 (D)ABD DC，AB ACB ADBADC，BDCDC BC，B
2、ADCADDB C，BDDC【解析】 当 BDDC，ABAC 时，因为 ADAD，由 SSS 可得ABDACD ，故 A 正确；当ADB ADC，BDCD 时，因为ADAD，由 SAS 可得 ABDACD，故 B 正确；当BC，BADCAD 时，因为 ADAD ，由 AAS 可得ABDACD，故 C 正确；D 不能判定ABDACD，因为不能利用 SSA 判定两三角形全等32016湖州 如图 223，已知在ABC 中，CD 是 AB 边上的高线，BE 平分ABC，交 CD 于点 E，BC5，DE2，则BCE 的面积等于 (C)A10 B7C5 D4图 223 【解析】 作 EFBC 于 F，BE
3、 平分ABC ，EDAB ，EFBC，EFDE2，来源:Zxxk.ComS BCE BCEF 525.12 124.2016宁波 如图 224，ABCD 中，E，F 是对角线 BD 上的两点，如果 添加一个条件，使ABE CDF，则添加的条件不能为 (C)ABEDF BBF DECAECF D12图 224【解析】 A当 BEDF ，ABE CDF(SAS)，故此选项可添加；B当 BFED，可得 BEDF ，ABECDF(SAS)，故此选项可添加；C当 AECF 无法得出ABECDF，故此选项符合题意；来源:学|科| 网 Z|X|X|KD当12，ABECDF( ASA)，故此选项可添加二、填空
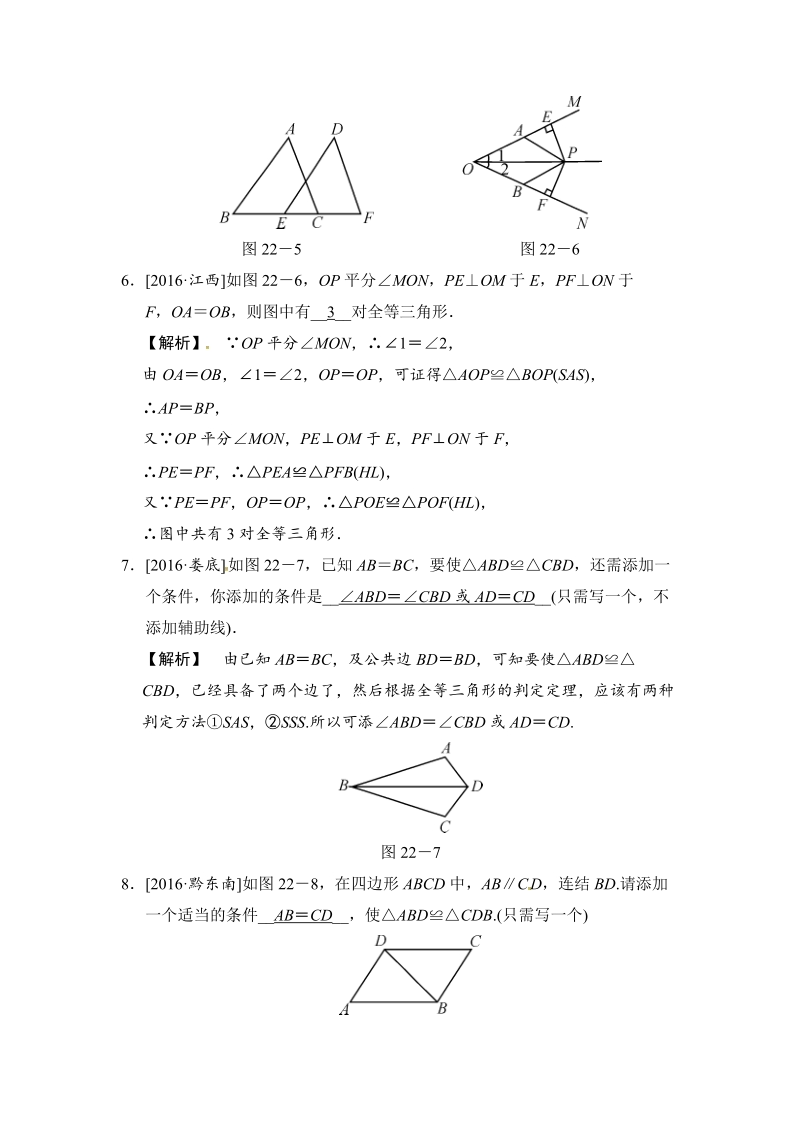
4、题(每题 5 分，共 20 分)52017长沙 如图 225，点 B，E，C，F 在一条直线上，ABDE，AB DE ，BECF，AC6，则 DF_6_.第 3 题答图图 225 图 22662016江西 如图 226，OP 平分MON，PEOM 于 E，PFON 于F，OA OB ，则图中有_ 3_对全等三角形【解析】 OP 平分MON，12，由 OA OB， 12，OPOP ，可证得AOPBOP(SAS )，APBP，又OP 平分MON，PEOM 于 E，PFON 于 F，PEPF，PEAPFB(HL)，又PEPF，OPOP ，POEPOF(HL)，图中共有 3 对全等三角形72016娄底
5、 如图 227，已知 ABBC，要使ABD CBD，还需添加一个条件，你添加的条件是_ABDCBD 或 ADCD_(只需写一个，不添加辅助线)【解析】 由已知 ABBC，及公共边 BDBD ，可知要使ABD CBD，已经具备了两个边了，然后根据全等三角形的判定定理，应该有两种判定方法SAS，SSS.所以可添ABDCBD 或 ADCD .图 22782016黔东南 如图 228，在四边形 ABCD 中，ABC D，连结 BD.请添加一个适当的条件_ABCD_，使ABDCDB.(只需写一个)图 228【解析】 ABCD，ABDCDB，而 BDDB，当添加 ABCD 时，可根据“SAS ”判定ABD
6、CDB.三、解答题(共 20 分)9(10 分)2016 福州如图 229，12，3 4，求证：ACAD.证明：34，ABCABD .在ABC 和ABD 中，1 2，AB AB，ABC ABD，)ABCABD (ASA)ACAD.10(10 分)2016 武汉如图 2210，点B，C，E，F 在同一直线上，BCEF，ACBC 于点 C，DFEF 于点F，ACDF.求证：(1)ABCDEF ；(2)ABDE .证明：(1)AC BC 于点 C，DFEF 于点 F，ACBDFE 90，在ABC 和DEF 中，BC EF，ACB DFE，AC DF， )ABC DEF(SAS)；(2)ABCDEF
7、，BDE F，ABDE.(24 分)图 229图 221011(12 分)2017 杭州如图 2211，在ABC 中， ABAC，点 E，F 分别在AB，AC 上，AE AF，BF 与 CE 相交于点 P，求证：PBPC ，并请直接写出图中其他相等的线段图 2211证明：ABAC，ABCACB，在ABF 与 ACE 中，AB AC，CAE BAF，AE AF， )ABF ACE(SAS)，ABF ACE，来源:学科网 ZXXKABCABFACBACE，FBCECB，PBPC.相等的线段还有：PEPF，BE CF，ECFB， AEAF.12(12 分)2016 温州如图 2212，点 C，E，F
8、， B 在同一直线上，点 A，D 在 BC 异侧，ABCD，AE DF， AD.(1)求证：ABCD；(2)若 ABCF，B30，求D 的度数解：(1)证明： AB CD，BC，来源:学.科.网在ABE 和 DCF 中，A D，C B，AE DF，)图 2212ABE DCF(AAS)，ABCD；(2)ABE DCF，ABCD，BE CF，ABCF，B 30，CDCF ，C B30，CDF 是等腰三角形，D (18030)75.12(16 分)13(16 分)2016 株洲如图 2213，在 RtABC 中，C90，BD 是 ABC的一条角平分线点 O，E，F 来源 :Z,xx,k.Com分别
9、在 BD，BC，AC 上，且四边形 OECF 是正方形(1)求证：点 O 在BAC 的平分线上；(2)若 AC5， BC12，求 OE 的长图 2213 解：(1)证明：过点 O 作 OMAB 于点 M，BD 是 ABC 的平分线，OE OM，四边形 OECF 是正方形，OE OF，OF OM，OM AB，OFAD，AO 是 BAC 的角平分线，第 13 题答图即点 O 在BAC 的平分线上；(2)在 RtABC 中，AC5，BC12，AB 13，AC2 BC2 52 122设 CECFx，BE BMy，AMAFz， x y 12，y z 13，x z 5，)解得 x 2，y 10，z 3，)OE CECF2.
