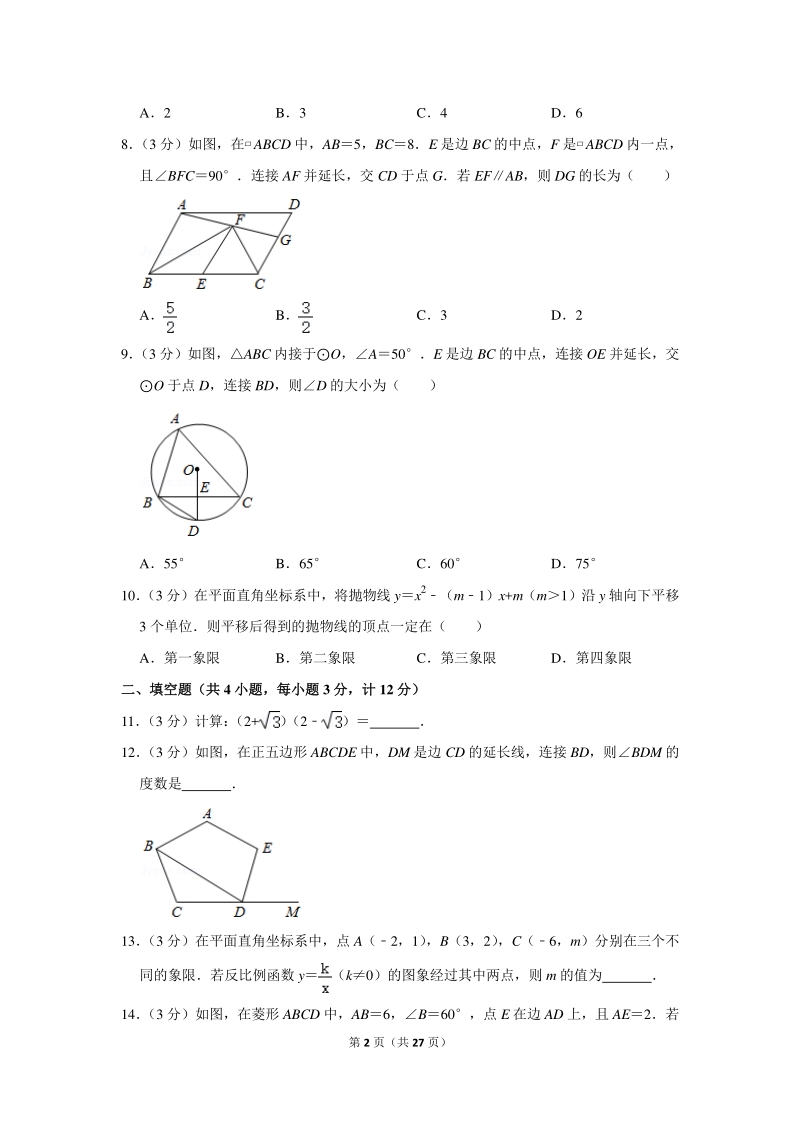
1、在平面直角坐标系中，O 为坐标原点若直线 yx+3 分别与 x 轴、直线 y2x 交于点 A、B，则AOB 的面积为（ ） 第 2 页（共 27 页） A2 B3 C4 D6 8 （3 分）如图，在ABCD 中，AB5，BC8E 是边 BC 的中点，F 是ABCD 内一点， 且BFC90连接 AF 并延长，交 CD 于点 G若 EFAB，则 DG 的长为（ ） A B C3 D2 9 （3 分）如图，ABC 内接于O，A50E 是边 BC 的中点，连接 OE 并延长，交 O 于点 D，连接 BD，则D 的大小为（ ）
2、 A55 B65 C60 D75 10 （3 分）在平面直角坐标系中，将抛物线 yx2（m1）x+m（m1）沿 y 轴向下平移 3 个单位则平移后得到的抛物线的顶点一定在（ ） A第一象限 B第二象限 C第三象限 D第四象限 二、填空题（共二、填空题（共 4 小题，每小题小题，每小题 3 分，计分，计 12 分）分） 11 （3 分）计算： （2+） （2） 12 （3 分）如图，在正五边形 ABCDE 中，DM 是边 CD 的延长线，连接 BD，则BDM 的 度数是 &nbs
3、p;13 （3 分）在平面直角坐标系中，点 A（2，1） ，B（3，2） ，C（6，m）分别在三个不 同的象限若反比例函数 y（k0）的图象经过其中两点，则 m 的值为 14 （3 分）如图，在菱形 ABCD 中，AB6，B60，点 E 在边 AD 上，且 AE2若 第 3 页（共 27 页） 直线 l 经过点 E，将该菱形的面积平分，并与菱形的另一边交于点 F，则线段 EF 的长 为 三、解答题（共三、解答题（共 11 小题，计小题，计 78 分解答应写出过程）分解答应写出过程） 15
4、 （5 分）解不等式组： 16 （5 分）解分式方程：1 17 （5 分）如图，已知ABC，ACAB，C45请用尺规作图法，在 AC 边上求作 一点 P，使PBC45 （保留作图痕迹不写作法） 18 （5 分）如图，在四边形 ABCD 中，ADBC，BCE 是边 BC 上一点，且 DE DC求证：ADBE 19 （7 分）王大伯承包了一个鱼塘，投放了 2000 条某种鱼苗，经过一段时间的精心喂养， 存活率大致达到了 90%他近期想出售鱼塘里的这种鱼为了估计鱼塘里这种鱼的总质 量，王大伯随机捕捞了 20 条鱼，分别称得其质量后放回鱼塘现将这 2
5、0 条鱼的质量作 为样本，统计结果如图所示： （1）这 20 条鱼质量的中位数是 ，众数是 （2）求这 20 条鱼质量的平均数； （3）经了解，近期市场上这种鱼的售价为每千克 18 元，请利用这个样本的平均数估 第 4 页（共 27 页） 计王大伯近期售完鱼塘里的这种鱼可收入多少元？ 20 （7 分）如图所示，小明家与小华家住在同一栋楼的同一单元，他俩想测算所住楼对面 商业大厦的高 MN他俩在小明家的窗台 B 处，测得商业大厦顶部 N 的仰角1 的度数， 由于楼下植物的遮挡，不能在 B
6、处测得商业大厦底部 M 的俯角的度数于是，他俩上楼 来到小华家， 在窗台 C 处测得大厦底部 M 的俯角2 的度数， 竟然发现1 与2 恰好相 等已知 A，B，C 三点共线，CAAM，NMAM，AB31m，BC18m，试求商业大 厦的高 MN 21 （7 分）某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术这种瓜苗早期 在农科所的温室中生长， 长到大约 20cm 时， 移至该村的大棚内， 沿插杆继续向上生长 研 究表明，60 天内，这种瓜苗生长的高度 y（cm）与生长时间 x（天）之间的关系大致如 图所示 （1）求 y 与 x 之间的函数关系式； （
7、2）当这种瓜苗长到大约 80cm 时，开始开花结果，试求这种瓜苗移至大棚后继续生 长大约多少天，开始开花结果？ 第 5 页（共 27 页） 22 （7 分）小亮和小丽进行摸球试验他们在一个不透明的空布袋内，放入两个红球，一 个白球和一个黄球，共四个小球这些小球除颜色外其它都相同试验规则：先将布袋 内的小球摇匀，再从中随机摸出一个小球，记下颜色后放回，称为摸球一次 （1）小亮随机摸球 10 次，其中 6 次摸出的是红球，求这 10 次中摸出红球的频率； （2）若小丽随机摸球两次，请利用画树状图或列表的方法，求这两次摸出的
8、球中一个是 白球、一个是黄球的概率 23 （8 分）如图，ABC 是O 的内接三角形，BAC75，ABC45连接 AO 并 延长，交O 于点 D，连接 BD过点 C 作O 的切线，与 BA 的延长线相交于点 E （1）求证：ADEC； （2）若 AB12，求线段 EC 的长 24 （10 分）如图，抛物线 yx2+bx+c 经过点（3，12）和（2，3） ，与两坐标轴的交点 分别为 A，B，C，它的对称轴为直线 l （1）求该抛物线的表达式； （2）P 是该抛物线上的点，过点 P 作 l 的垂线，垂足为 D，E 是 l
9、上的点要使以 P、D、 E 为顶点的三角形与AOC 全等，求满足条件的点 P，点 E 的坐标 第 6 页（共 27 页） 25 （12 分）问题提出 （1） 如图 1， 在 RtABC 中， ACB90， ACBC， ACB 的平分线交 AB 于点 D 过 点 D 分别作 DEAC，DFBC垂足分别为 E，F，则图 1 中与线段 CE 相等的线段 是 问题探究 （2） 如图 2， AB 是半圆 O 的直径， AB8 P 是上一点， 且2， 连接 AP， BP APB 的平分线交
10、AB 于点 C，过点 C 分别作 CEAP，CFBP，垂足分别为 E，F，求线 段 CF 的长 问题解决 （3）如图 3，是某公园内“少儿活动中心”的设计示意图已知O 的直径 AB70m， 点 C 在O 上， 且 CACB P 为 AB 上一点， 连接 CP 并延长， 交O 于点 D 连接 AD， BD过点 P 分别作 PEAD，PFBD，重足分别为 E，F按设计要求，四边形 PEDF 内部为室内活动区， 阴影部分是户外活动区， 圆内其余部分为绿化区 设 AP 的长为 x （m） ， 阴影部分的面积为 y（m2） 求 y 与 x 之间的函数关系式； &nb
11、sp;按照 “少儿活动中心” 的设计要求， 发现当 AP 的长度为 30m 时， 整体布局比较合理 试 求当 AP30m 时室内活动区（四边形 PEDF）的面积 第 7 页（共 27 页） 第 8 页（共 27 页） 2020 年陕西省中考数学试卷年陕西省中考数学试卷 参考答案与试题解析参考答案与试题解析 一、选择题（共一、选择题（共 10 小题，每小题小题，每小题 3 分，计分，计 30 分每小题只有一个选项是符合题意的）分每小题只有一个选项是符合题意的） 1 （3 分）18
12、 的相反数是（ ） A18 B18 C D 【分析】直接利用相反数的定义得出答案 【解答】解：18 的相反数是：18 故选：A 【点评】此题主要考查了相反数，正确把握相反数的定义是解题关键 2 （3 分）若A23，则A 余角的大小是（ ） A57 B67 C77 D157 【分析】根据A 的余角是 90A，代入求出即可 【解答】解：A23， A 的余角是 902367 故选：B 【点评】本题考查了互余的应用，注意：如果A 和B 互为余角，那么A90 B
13、 3 （3 分）2019 年，我国国内生产总值约为 990870 亿元，将数字 990870 用科学记数法表示 为（ ） A9.9087105 B9.9087104 C99.087104 D99.087103 【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相 同 【解答】解：9908709.9087105， 故选：A 【点评】此题考查科学记数法的表示方法科学记数法的表示形式为 a10n的形式，其 中
14、1|a|10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值 4 （3 分）如图，是 A 市某一天的气温随时间变化的情况，则这天的日温差（最高气温与最 第 9 页（共 27 页） 低气温的差）是（ ） A4 B8 C12 D16 【分析】根据 A 市某一天内的气温变化图，分析变化趋势和具体数值，即可求出答案 【解答】解：从折线统计图中可以看出，这一天中最高气温 8，最低气温是4，这 一天中最高气温与最低气温的差为 12， 故选：C 【点评】本题考查了函数图象，认真观察函数图象图，从图
15、中得到必要的信息是解决问 题的关键 5 （3 分）计算： （x2y）3（ ） A2x6y3 Bx6y3 Cx6y3 Dx5y4 【分析】根据积的乘方运算法则计算即可，积的乘方，等于每个因式乘方的积 【解答】解： （x2y）3 故选：C 【点评】本题主要考查了幂的乘方与积的乘方，熟记幂的运算法则是解答本题的关键 6 （3 分）如图，在 33 的网格中，每个小正方形的边长均为 1，点 A，B，C 都在格点上， 若 BD 是ABC 的高，则 BD 的长为（ ） A B C D 【分析】根据勾
16、股定理计算 AC 的长，利用面积差可得三角形 ABC 的面积，由三角形的 面积公式即可得到结论 第 10 页（共 27 页） 【解答】解：由勾股定理得：AC， SABC333.5， ， ， BD， 故选：D 【点评】本题考查了勾股定理，三角形的面积的计算，掌握勾股定理是解题的关键 7 （3 分）在平面直角坐标系中，O 为坐标原点若直线 yx+3 分别与 x 轴、直线 y2x 交于点 A、B，则AOB 的面积为（ ） A2 B3 C4 D6 【分析】
17、根据方程或方程组得到 A（3，0） ，B（1，2） ，根据三角形的面积公式即可 得到结论 【解答】解：在 yx+3 中，令 y0，得 x3， 解得， A（3，0） ，B（1，2） ， AOB 的面积323， 故选：B 【点评】本题考查了直线围成图形面积问题，其中涉及了一次函数的性质，三角形的面 积的计算，正确的理解题意是解题的关键 8 （3 分）如图，在ABCD 中，AB5，BC8E 是边 BC 的中点，F 是ABCD 内一点， 且BFC90连接 AF 并延长，交 CD 于点 G若 EFAB，则 DG 的长为（
18、 ） A B C3 D2 【分析】 依据直角三角形斜边上中线的性质， 即可得到 EF 的长， 再根据梯形中位线定理， 即可得到 CG 的长，进而得出 DG 的长 第 11 页（共 27 页） 【解答】解：E 是边 BC 的中点，且BFC90， RtBCF 中，EFBC4， EFAB，ABCG，E 是边 BC 的中点， F 是 AG 的中点， EF 是梯形 ABCG 的中位线， CG2EFAB3， 又CDAB5， DG532， 故选：D
19、 【点评】本题主要考查了平行四边形的性质以及梯形中位线定理，梯形的中位线平行于 两底，并且等于两底和的一半 9 （3 分）如图，ABC 内接于O，A50E 是边 BC 的中点，连接 OE 并延长，交 O 于点 D，连接 BD，则D 的大小为（ ） A55 B65 C60 D75 【分析】连接 CD，根据圆内接四边形的性质得到CDB180A130，根据垂 径定理得到 ODBC，求得 BDCD，根据等腰三角形的性质即可得到结论 【解答】解：连接 CD， A50， CDB180A130， E 是边 BC
20、 的中点， ODBC， BDCD， ODBODCBDC65， 故选：B 第 12 页（共 27 页） 【点评】本题考查了三角形的外接圆与外心，圆内接四边形的性质，垂径定理，等腰三 角形的性质，正确的理解题意是解题的关键 10 （3 分）在平面直角坐标系中，将抛物线 yx2（m1）x+m（m1）沿 y 轴向下平移 3 个单位则平移后得到的抛物线的顶点一定在（ ） A第一象限 B第二象限 C第三象限 D第四象限 【分析】根据平移规律得到平移后抛物线的顶点坐标，然后
21、结合 m 的取值范围判断新抛 物线的顶点所在的象限即可 【解答】解：yx2（m1）x+m（x）2+m， 该抛物线顶点坐标是（，m） ， 将其沿 y 轴向下平移 3 个单位后得到的抛物线的顶点坐标是 （， m3） ， m1， m10， 0， m310， 点（，m3）在第四象限； 故选：D 【点评】本题考查了二次函数的图象与性质、平移的性质、抛物线的顶点坐标等知识； 熟练掌握二次函数的图象和性质，求出抛物线的顶点坐标是解题的关键 二、填空题（共二、填空题（共 4 小题
22、，每小题小题，每小题 3 分，计分，计 12 分）分） 11 （3 分）计算： （2+） （2） 1 【分析】先利用平方差公式展开得到原式22（）2，再利用二次根式的性质化简， 然后进行减法运算 【解答】解：原式22（）2 43 第 13 页（共 27 页） 1 【点评】本题考查了二次根式的混合运算：在二次根式的混合运算中，如能结合题目特 点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍 12 （3 分）如图，在正五边形 ABCDE 中，DM 是边 CD 的延长线，连
23、接 BD，则BDM 的 度数是 144 【分析】根据正五边形的性质和内角和为 540，求得每个内角的度数为 108，再结合 等腰三角形和邻补角的定义即可解答 【解答】解：因为五边形 ABCDE 是正五边形， 所以C108，BCDC， 所以BDC36， 所以BDM18036144， 故答案为：144 【点评】本题考查了正五边形解题的关键是掌握正五边形的性质：各边相等，各角相 等，内角和为 540熟记定义是解题的关键 13 （3 分）在平面直角坐标系中，点 A（2，1） ，B（3，2） ，
24、C（6，m）分别在三个不 同的象限若反比例函数 y（k0）的图象经过其中两点，则 m 的值为 1 【分析】根据已知条件得到点 A（2，1）在第二象限，求得点 C（6，m）一定在第 三象限，由于反比例函数 y（k0）的图象经过其中两点，于是得到反比例函数 y （k0）的图象经过 B（3，2） ，C（6，m） ，于是得到结论 【解答】解：点 A（2，1） ，B（3，2） ，C（6，m）分别在三个不同的象限，点 A （2，1）在第二象限， 点 C（6，m）一定在第三象限， B（3，2）在第一象限，反比例函数 y（k0）的图象经过其中两点，
25、; 第 14 页（共 27 页） 反比例函数 y（k0）的图象经过 B（3，2） ，C（6，m） ， 326m， m1， 故答案为：1 【点评】本题考查了反比例函数图象上点的坐标特征，正确的理解题意是解题的关键 14 （3 分）如图，在菱形 ABCD 中，AB6，B60，点 E 在边 AD 上，且 AE2若 直线 l 经过点 E，将该菱形的面积平分，并与菱形的另一边交于点 F，则线段 EF 的长为 2 【分析】过点 A 和点 E 作 AGBC，EHBC 于点 G 和 H，
26、可得矩形 AGHE，再根据菱 形 ABCD 中，AB6，B60，可得 BG3，AG3EH，由题意可得，FHFC HC211，进而根据勾股定理可得 EF 的长 【解答】解：如图，过点 A 和点 E 作 AGBC，EHBC 于点 G 和 H， 得矩形 AGHE， GHAE2， 在菱形 ABCD 中，AB6，B60， BG3，AG3EH， HCBCBGGH6321， EF 平分菱形面积， FCAE2， FHFCHC211， 在 RtEFH 中，根据勾股定理，得 EF2
27、 第 15 页（共 27 页） 故答案为：2 【点评】本题考查了菱形的性质，解决本题的关键是掌握菱形的性质 三、解答题（共三、解答题（共 11 小题，计小题，计 78 分解答应写出过程）分解答应写出过程） 15 （5 分）解不等式组： 【分析】分别求出不等式组中两不等式的解集，找出两解集的公共部分即可 【解答】解：， 由得：x2， 由得：x3， 则不等式组的解集为 2x3 【点评】此题考查了解一元一次不等式组，熟练掌握不等式组的解法是解本题的关键
28、 16 （5 分）解分式方程：1 【分析】分式方程去分母转化为整式方程，求出整式方程的解得到 x 的值，经检验即可 得到分式方程的解 【解答】解：方程1， 去分母得：x24x+43xx22x， 解得：x， 经检验 x是分式方程的解 【点评】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验 17 （5 分）如图，已知ABC，ACAB，C45请用尺规作图法，在 AC 边上求作 一点 P，使PBC45 （保留作图痕迹不写作法） 【分析】 根据尺规作图法， 作一个角等于已知角， 在
29、AC 边上求作一点 P， 使PBC45 第 16 页（共 27 页） 即可 【解答】解：如图，点 P 即为所求 【点评】本题考查了作图基本作图，解决本题的关键是掌握基本作图方法 18 （5 分）如图，在四边形 ABCD 中，ADBC，BCE 是边 BC 上一点，且 DE DC求证：ADBE 【分析】根据等边对等角的性质求出DECC，再由BC 得DECB，所 以 ABDE，得出四边形 ABED 是平行四边形，进而得出结论 【解答】证明：DEDC， DECC BC， BD
30、EC， ABDE， ADBC， 四边形 ABED 是平行四边形 ADBE 【点评】本题主要考查了平行四边形的判定和性质解题的关键是熟练掌握平行四边形 的判定定理和性质定理的运用 19 （7 分）王大伯承包了一个鱼塘，投放了 2000 条某种鱼苗，经过一段时间的精心喂养， 存活率大致达到了 90%他近期想出售鱼塘里的这种鱼为了估计鱼塘里这种鱼的总质 量，王大伯随机捕捞了 20 条鱼，分别称得其质量后放回鱼塘现将这 20 条鱼的质量作 为样本，统计结果如图所示： 第 17 页（共 27 页） &nbs
31、p; （1）这 20 条鱼质量的中位数是 1.45kg ，众数是 1.5kg （2）求这 20 条鱼质量的平均数； （3）经了解，近期市场上这种鱼的售价为每千克 18 元，请利用这个样本的平均数估 计王大伯近期售完鱼塘里的这种鱼可收入多少元？ 【分析】 （1）根据中位数和众数的定义求解可得； （2）利用加权平均数的定义求解可得； （3）用单价乘以（2）中所得平均数，再乘以存活的数量，从而得出答案 【解答】解： （1）这 20 条鱼质量的中位数是第 10、11 个数据的平均数，且第 10、11 个数据分别为 1.4、1.
32、5， 这 20 条鱼质量的中位数是1.45（kg） ，众数是 1.5kg， 故答案为：1.45kg，1.5kg （2） 1.45（kg） ， 这 20 条鱼质量的平均数为 1.45kg； （3）181.45200090%46980（元） ， 答：估计王大伯近期售完鱼塘里的这种鱼可收入 46980 元 【点评】本题考查了用样本估计总体、加权平均数、众数及中位数的知识，解题的关键 是正确的用公式求得加权平均数，难度不大 20 （7 分）如图所示，小明家与小华家住在同一栋楼的同一单元，他俩想测算所住楼
33、对面 商业大厦的高 MN他俩在小明家的窗台 B 处，测得商业大厦顶部 N 的仰角1 的度数， 由于楼下植物的遮挡，不能在 B 处测得商业大厦底部 M 的俯角的度数于是，他俩上楼 来到小华家， 在窗台 C 处测得大厦底部 M 的俯角2 的度数， 竟然发现1 与2 恰好相 第 18 页（共 27 页） 等已知 A，B，C 三点共线，CAAM，NMAM，AB31m，BC18m，试求商业大 厦的高 MN 【分析】过点 C 作 CEMN 于点 E，过点 B 作 BFMN 于点 F，可得四边形 AMEC 和四 边形 AMFB 均为矩形，可以证明BFNCEM，得 N
34、FEM49，进而可得商业大厦 的高 MN 【解答】解：如图，过点 C 作 CEMN 于点 E，过点 B 作 BFMN 于点 F， CEFBFE90， CAAM，NMAM， 四边形 AMEC 和四边形 AMFB 均为矩形， CEBF，MEAC， 12， BFNCEM（ASA） ， NFEM31+1849， 由矩形性质可知：EFCB18， MNNF+EMEF49+491880（m） 答：商业大厦的高 MN 为 80m 【点评】本题考查了全等三角形的判定
35、与性质，解决本题的关键是掌握仰角俯角定义， 第 19 页（共 27 页） 构造全等三角形解决问题 21 （7 分）某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术这种瓜苗早期 在农科所的温室中生长， 长到大约 20cm 时， 移至该村的大棚内， 沿插杆继续向上生长 研 究表明，60 天内，这种瓜苗生长的高度 y（cm）与生长时间 x（天）之间的关系大致如 图所示 （1）求 y 与 x 之间的函数关系式； （2）当这种瓜苗长到大约 80cm 时，开始开花结果，试求这种瓜苗移至大棚后继续生 长大约多少天，开始开花结果？ &nbs
36、p; 【分析】 （1）分段函数，利用待定系数法解答即可； （2）利用（1）的结论，把 y80 代入求出 x 的值即可解答 【解答】解： （1）当 0 x15 时，设 ykx（k0） ， 则：2015k， 解得 k， y； 当 15x60 时，设 ykx+b（k0） ， 则：， 解得， y， ； 第 20 页（共 27 页） （2）当 y80 时，80，解得 x33， 331518（天） ， 这种瓜苗移至大棚后继
37、续生长大约 18 天，开始开花结果 【点评】本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，已知 函数值求自变量的值，仔细观察图象，准确获取信息是解题的关键 22 （7 分）小亮和小丽进行摸球试验他们在一个不透明的空布袋内，放入两个红球，一 个白球和一个黄球，共四个小球这些小球除颜色外其它都相同试验规则：先将布袋 内的小球摇匀，再从中随机摸出一个小球，记下颜色后放回，称为摸球一次 （1）小亮随机摸球 10 次，其中 6 次摸出的是红球，求这 10 次中摸出红球的频率； （2）若小丽随机摸球两次，请利用画树状图或列表的方法，求这两次
38、摸出的球中一个是 白球、一个是黄球的概率 【分析】 （1）由频率定义即可得出答案； （2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸出的球中 一个是白球、一个是黄球的情况，利用概率公式求解即可求得答案 【解答】解： （1）小亮随机摸球 10 次，其中 6 次摸出的是红球，这 10 次中摸出红球的 频率； （2）画树状图得： 共有 16 种等可能的结果，两次摸出的球中一个是白球、一个是黄球的有 2 种情况， 两次摸出的球中一个是白球、一个是黄球的概率 【点评】本题考查的是用列表法或画树状图
39、法求概率注意列表法或树状图法可以不重 复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或 两步以上完成的事件注意概率所求情况数与总情况数之比 23 （8 分）如图，ABC 是O 的内接三角形，BAC75，ABC45连接 AO 并 延长，交O 于点 D，连接 BD过点 C 作O 的切线，与 BA 的延长线相交于点 E （1）求证：ADEC； 第 21 页（共 27 页） （2）若 AB12，求线段 EC 的长 【分析】（1） 连接 OC， 由切线的性质可得OCE90， 由圆周角定理可得AOC9
40、0， 可得结论； （2）过点 A 作 AFEC 交 EC 于 F，由锐角三角函数可求 AD8，可证四边形 OAFC 是正方形，可得 CFAF4，由锐角三角函数可求 EF12，即可求解 【解答】证明： （1）连接 OC， CE 与O 相切于点 C， OCE90， ABC45， AOC90， AOC+OCE180， ADEC （2）如图，过点 A 作 AFEC 交 EC 于 F， 第 22 页（共 27 页） BAC75，ABC45， &
41、nbsp;ACB60， DACB60， sinADB， AD8， OAOC4， AFEC，OCE90，AOC90， 四边形 OAFC 是矩形， 又OAOC， 四边形 OAFC 是正方形， CFAF4， BAD90D30， EAF180903060， tanEAF， EFAF12， CECF+EF12+4 【点评】本题考查了切线的性质，圆周角定理，锐角三角函数，正方形的判定和性质， 熟练运用这些性质进行推理是本题的关键
42、 24 （10 分）如图，抛物线 yx2+bx+c 经过点（3，12）和（2，3） ，与两坐标轴的交点 分别为 A，B，C，它的对称轴为直线 l （1）求该抛物线的表达式； 第 23 页（共 27 页） （2）P 是该抛物线上的点，过点 P 作 l 的垂线，垂足为 D，E 是 l 上的点要使以 P、D、 E 为顶点的三角形与AOC 全等，求满足条件的点 P，点 E 的坐标 【分析】 （1）将点（3，12）和（2，3）代入抛物线表达式，即可求解； （2）由题意得：PDDE3 时，以 P、D、E 为顶点的三角
43、形与AOC 全等，分点 P 在抛物线对称轴右侧、点 P 在抛物线对称轴的左侧两种情况，分别求解即可 【解答】解： （1）将点（3，12）和（2，3）代入抛物线表达式得，解 得， 故抛物线的表达式为：yx2+2x3； （2）抛物线的对称轴为 x1，令 y0，则 x3 或 1，令 x0，则 y3， 故点 A、B 的坐标分别为（3，0） 、 （1，0） ；点 C（0，3） ， 故 OAOC3， PDEAOC90， 当 PDDE3 时，以 P、D、E 为顶点的三角形与AOC 全等， 设点 P（m，n） ，
44、当点 P 在抛物线对称轴右侧时，m（1）3，解得：m2， 故 n22+2255，故点 P（2，5） ， 故点 E（1，2）或（1，8） ； 当点 P 在抛物线对称轴的左侧时，由抛物线的对称性可得，点 P（4，5） ，此时点 E 坐 标同上， 综上，点 P 的坐标为（2，5）或（4，5） ；点 E 的坐标为（1，2）或（1，8） 【点评】本题考查的是二次函数综合运用，涉及到三角形全等等，有一定的综合性，难 度适中，其中（2）需要分类求解，避免遗漏 第 24 页（共 27 页） 25 （12 分）
45、问题提出 （1） 如图 1， 在 RtABC 中， ACB90， ACBC， ACB 的平分线交 AB 于点 D 过 点 D 分别作 DEAC，DFBC垂足分别为 E，F，则图 1 中与线段 CE 相等的线段是 CF、DE、DF 问题探究 （2） 如图 2， AB 是半圆 O 的直径， AB8 P 是上一点， 且2， 连接 AP， BP APB 的平分线交 AB 于点 C，过点 C 分别作 CEAP，CFBP，垂足分别为 E，F，求线 段 CF 的长 问题解决 （3）如图 3，是某公园内“少儿活动中心”的设计
46、示意图已知O 的直径 AB70m， 点 C 在O 上， 且 CACB P 为 AB 上一点， 连接 CP 并延长， 交O 于点 D 连接 AD， BD过点 P 分别作 PEAD，PFBD，重足分别为 E，F按设计要求，四边形 PEDF 内部为室内活动区， 阴影部分是户外活动区， 圆内其余部分为绿化区 设 AP 的长为 x （m） ， 阴影部分的面积为 y（m2） 求 y 与 x 之间的函数关系式； 按照 “少儿活动中心” 的设计要求， 发现当 AP 的长度为 30m 时， 整体布局比较合理 试 求当 AP30m 时室内活动区（四边形 PEDF）的面积 【
47、分析】 （1）证明四边形 CEDF 是正方形，即可得出结果； （2）连接 OP，由 AB 是半圆 O 的直径，2，得出APB90，AOP60， 则ABP30，同（1）得四边形 PECF 是正方形，得 PFCF，在 RtAPB 中，PB ABcosABP4，在 RtCFB 中，BFCF，推出 PBCF+BF， 即可得出结果； （3）同（1）得四边形 DEPF 是正方形，得出 PEPF，APE+BPF90，PEA 第 25 页（共 27 页） PFB90，将APE 绕点 P 逆时针旋转 90，得到APF，PAPA，则 A、 F、B 三点共线，AP
48、EAPF，证APB90，得出 SPAE+SPBFSPAB PAPBx（70 x） ，在 RtACB 中，ACBC35，SACBAC21225，由 ySPAB+SACB，即可得出结果； 当 AP30 时，AP30，PB40，在 RtAPB 中，由勾股定理得 AB 50，由 SAPBABPFPBAP，求 PF，即可得出结果 【解答】解： （1）ACB90，DEAC，DFBC， 四边形 CEDF 是矩形， CD 平分ACB，DEAC，DFBC， DEDF， 四边形 CEDF 是正方形， CECFDEDF，
49、;故答案为：CF、DE、DF； （2）连接 OP，如图 2 所示： AB 是半圆 O 的直径，2， APB90，AOP18060， ABP30， 同（1）得：四边形 PECF 是正方形， PFCF， 在 RtAPB 中，PBABcosABP8cos3084， 在 RtCFB 中，BFCF， PBPF+BF， PBCF+BF， 即：4CF+CF， 解得：CF62； （3）AB 为O 的直径， ACBADB90， &n
50、bsp;第 26 页（共 27 页） CACB， ADCBDC， 同（1）得：四边形 DEPF 是正方形， PEPF，APE+BPF90，PEAPFB90， 将APE 绕点 P 逆时针旋转 90，得到APF，PAPA，如图 3 所示： 则 A、F、B 三点共线，APEAPF， APF+BPF90，即APB90， SPAE+SPBFSPABPAPBx（70 x） ， 在 RtACB 中，ACBCAB7035， SACBAC2（35）21225， ySPAB+SAC
51、Bx（70 x）+1225x2+35x+1225； 当 AP30 时，AP30，PBABAP703040， 在 RtAPB 中，由勾股定理得：AB50， SAPBABPFPBAP， 50PF4030， 解得：PF24， S四边形PEDFPF2242576（m2） ， 当 AP30m 时室内活动区（四边形 PEDF）的面积为 576m2 第 27 页（共 27 页） 【点评】本题是圆综合题，主要考查了圆周角定理、勾股定理、矩形的判定、正方形的 判定与性质、角平分线的性质、旋转的性质、三角函数定义、三角形面积与正方形面积 的计算等知识；熟练掌握圆周角定理和正方形的判定与性质是解题的关键
