1、山东省淄博市周村区山东省淄博市周村区 2020 年年中考数学一模试卷中考数学一模试卷(解析版解析版) 一、选择题：本题共一、选择题：本题共 12 小题，在每小题所给出的四个选项中，只有一个是正确的每小题小题，在每小题所给出的四个选项中，只有一个是正确的每小题 4 分，错选、不选或选出的答案超过一个，均记零分分，错选、不选或选出的答案超过一个，均记零分 1如果 a 是无理数，那么下列各数中，一定是有理数的是（ ） Aa Ba2 C Da0 2下列几何体中，俯视图为三角形的是（ ） A B C D 3下列各式，计算结果等于 2 3 的是（ ） A2225 B2522 C2225 D （2）（2）（
2、2） 4若 4k5，则 k 的可能值是（ ） A B C2 D 5某排球队 6 名场上队员的身高（单位：cm）是：180，184，188，190，192，194现用 一名身高为 186cm 的队员换下场上身高为 192cm 的队员，与换人前相比，场上队员的身 高（ ） A平均数变小，中位数变小 B平均数变小，中位数变大 C平均数变大，中位数变小 D平均数变大，中位数变大 6只有 1 和它本身两个因数且大于 1 的自然数叫做素数，我国数学家陈景润在有关素数的 “哥德巴赫猜想”的研究中取得了世界领先的成果若从 5，6，7，9 这 4 个数中随机抽 取一个，则抽到的数是素数的概率是（ ） A B C
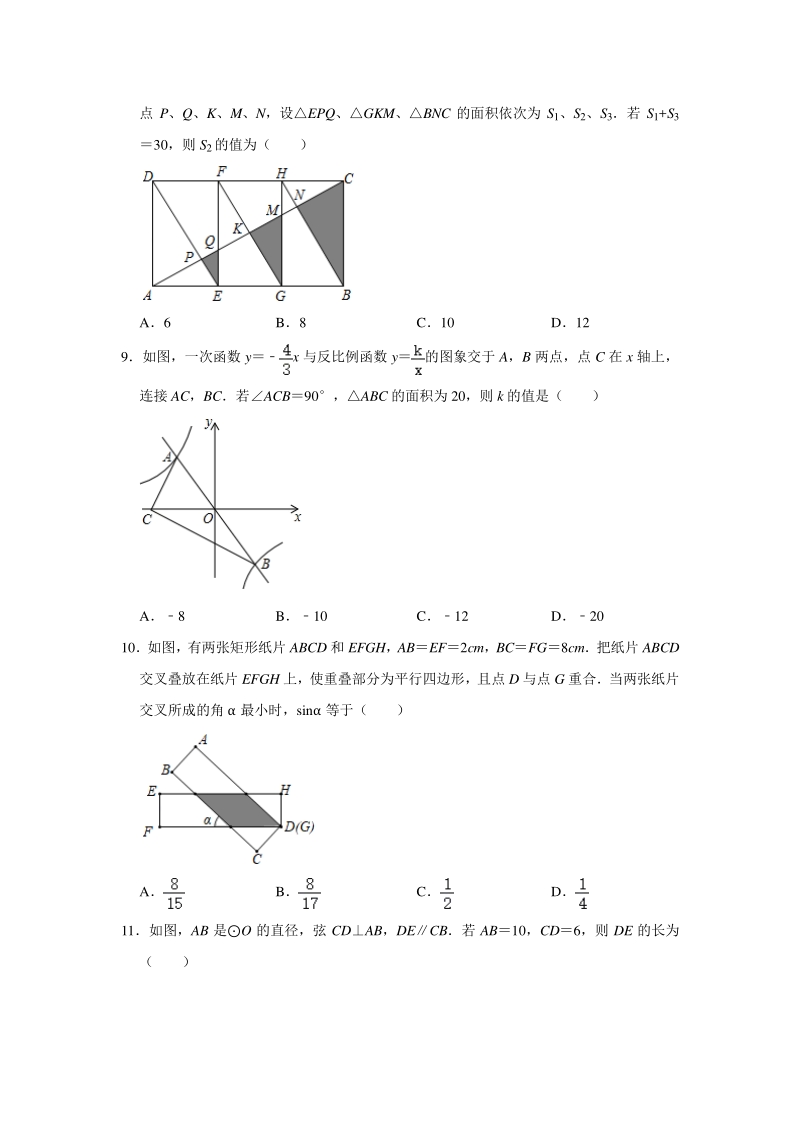
3、 D1 7下列长度的三条线段能组成锐角三角形的是（ ） A2，3，4 B2，3，5 C3，4，4 D3，4，5 8如图，矩形 ABCD 是由三个全等矩形拼成的，AC 与 DE、EF、FG、HG、HB 分别交于 点 P、Q、K、M、N，设EPQ、GKM、BNC 的面积依次为 S1、S2、S3若 S1+S3 30，则 S2的值为（ ） A6 B8 C10 D12 9如图，一次函数 yx 与反比例函数 y的图象交于 A，B 两点，点 C 在 x 轴上， 连接 AC，BC若ACB90，ABC 的面积为 20，则 k 的值是（ ） A8 B10 C12 D20 10如图，有两张矩形纸片 ABCD 和 E
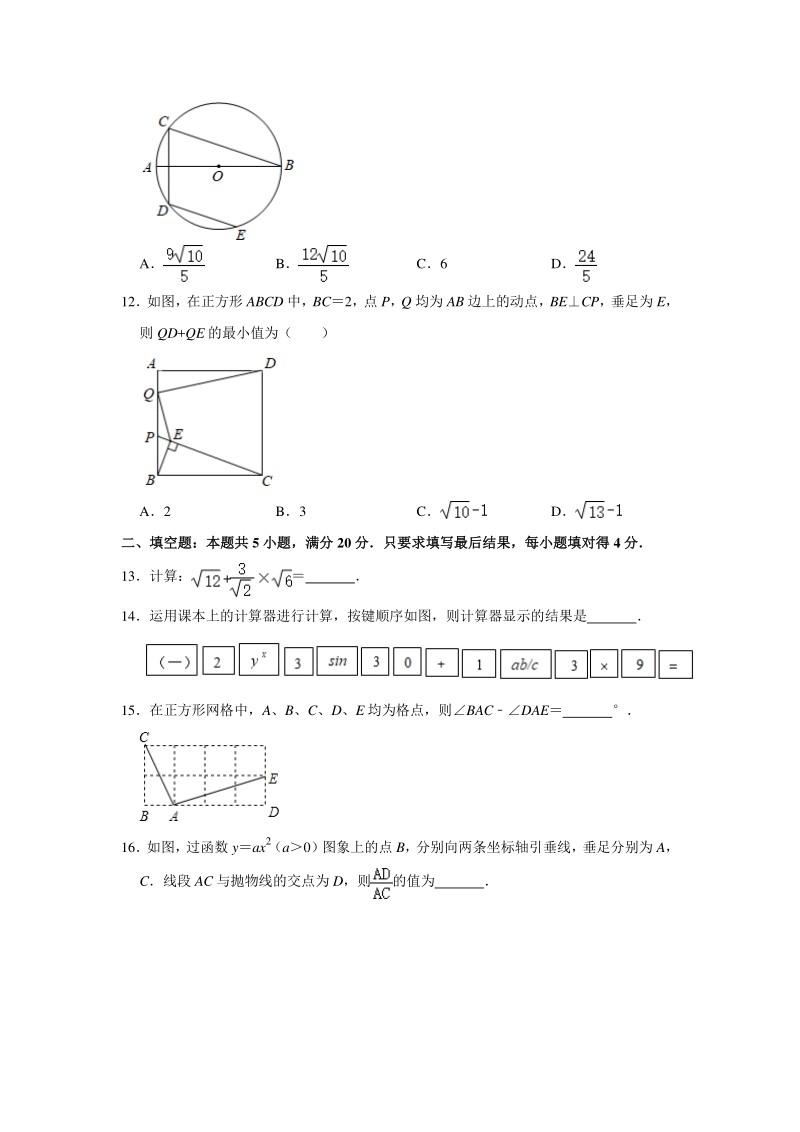
4、FGH，ABEF2cm，BCFG8cm把纸片 ABCD 交叉叠放在纸片 EFGH 上，使重叠部分为平行四边形，且点 D 与点 G 重合当两张纸片 交叉所成的角 最小时，sin 等于（ ） A B C D 11如图，AB 是O 的直径，弦 CDAB，DECB若 AB10，CD6，则 DE 的长为 （ ） A B C6 D 12如图，在正方形 ABCD 中，BC2，点 P，Q 均为 AB 边上的动点，BECP，垂足为 E， 则 QD+QE 的最小值为（ ） A2 B3 C D 二、填空题：本题共二、填空题：本题共 5 小题，满分小题，满分 20 分只要求填写最后结果，每小题填对得分只要求填写最后结
5、果，每小题填对得 4 分分 13计算： 14运用课本上的计算器进行计算，按键顺序如图，则计算器显示的结果是 15在正方形网格中，A、B、C、D、E 均为格点，则BACDAE 16 如图， 过函数 yax2（a0）图象上的点 B，分别向两条坐标轴引垂线， 垂足分别为 A， C线段 AC 与抛物线的交点为 D，则的值为 17如图，在 RtABC 中，C90，AC2，BC4点 M1，N1，P1分别在 AC，BC， AB 上，且四边形 M1CN1P1是正方形，点 M2，N2，P2分别在 P1N1，BN1，BP1上，且四 边形 M2N1N2P2是正方形，点 Mn，Nn，Pn分别在 Pn1Nn1，BNn1
6、，BPn1上，且 四边形 MnNn1NnPn是正方形，则线段 BN2020的长度是 三、解答题：本大题共三、解答题：本大题共 7 小题，共小题，共 52 分要写出必要的文字说明、证明过程或演算步骤分要写出必要的文字说明、证明过程或演算步骤 18 （5 分）化简：（x+2） 19 （5 分）如图，在ABC 中，A30，B45，AC，求 AB 的长 20 （8 分）我市某校招聘数学教师，本次招聘进行专业技能笔试和课堂教学展示两个项目 的考核，这两项考核的满分均为 100 分，学校将这两个项目的得分按一定的比例计算出 总成绩经统计，参加考核的 4 名考生的两个项目的得分如下： 考生序号 1 2 3
7、4 专业技能笔试 90 70 86 75 课堂教学展示 70 90 80 86 （1）经过计算，1 号考生的总成绩为 78 分，求专业技能笔试得分和课堂教学展示得分分 别占总成绩的百分比； （2）若学校录取总成绩最高的考生，通过计算说明 4 名考生中哪一名考生会被录取？ 21 （8 分）已知关于 x 的一元二次方程 kx2+（12k）x+k20 （1）若方程有两个不相等的实数根，求 k 的取值范围； （2） 当k取满足 （1） 中条件的最小整数时， 设方程的两根为和， 求代数式3+2+2016 的值 22 （8 分）在ABCD 中，经过 A、B、C 三点的O 与 AD 相切于点 A，经过点 C
8、 的切线与 AD 的延长线相交于点 P，连接 AC （1）求证：ABAC； （2）若 AB4，O 的半径为，求 PD 的长 23 （9 分）已知在 RtABC 中，ABC90，ABBC，将ABC 绕点 A 逆时针方向旋 转，得到ADE，旋转角为 （090） ，直线 BD 与 CE 交于点 F （1）如图 1，当 45时，求证：CFEF； （2）如图 2，在旋转过程中，当 为任意锐角时， CFB 的度数是否变化？若不变，请求出它的度数； 结论“CFEF” ，是否仍然成立？请说明理由 24 （9 分）如图，在平面直角坐标系中，直线 ykx7 与 y 轴交于点 C，与 x 轴交于点 B， 抛物线 y
9、ax2+bx+14a 经过 B、C 两点，与 x 轴的正半轴交于另一点 A，且 OA：OC2： 7 （1）求抛物线的解析式； （2）点 D 在线段 CB 上，点 P 在对称轴的左侧抛物线上，PDPB，当 tanPDB2， 求点 P 的坐标； （3）在（2）的条件下，点 Q（7，n）在第四象限，点 R 在对称轴的右侧抛物线上，若 以点 P、D、Q、R 为顶点的四边形为平行四边形，求点 Q、R 的坐标 2020 年山东省淄博市周村区中考数学一模试卷年山东省淄博市周村区中考数学一模试卷 参考答案与试题解析参考答案与试题解析 一、选择题：本题共一、选择题：本题共 12 小题，在每小题所给出的四个选项中
10、，只有一个是正确的每小题小题，在每小题所给出的四个选项中，只有一个是正确的每小题 4 分，错选、不选或选出的答案超过一个，均记零分分，错选、不选或选出的答案超过一个，均记零分 1如果 a 是无理数，那么下列各数中，一定是有理数的是（ ） Aa Ba2 C Da0 【分析】根据有理数和无理数的定义解答 【解答】解：A、如果 a 是无理数，那么a 一定是无理数，故这个选项错误； B、如果 a 是无理数，那么 a2可能是无理数，也可能是有理数，故这个选项错误； C、如果 a 是无理数，那么一定是无理数，故这个选项错误； D、如果 a 是无理数，那么 a0一定是有理数，因为 a01，故这个选项正确 故
11、选：D 【点评】本题考查了有理数和无理数的定义，解题的关键是熟练掌握有理数和无理数的 定义 2下列几何体中，俯视图为三角形的是（ ） A B C D 【分析】注意几何体的特征，主视图与左视图的高相同，主视图与俯视图的长相等，左 视图与俯视图的宽相同 【解答】解：根据俯视图的特征，应选 C 故选：C 【点评】本题考查了几何体的三视图，正确理解主视图与左视图以及俯视图的特征是解 题的关键 3下列各式，计算结果等于 2 3 的是（ ） A2225 B2522 C2225 D （2）（2）（2） 【分析】根据负整数指数幂、同底数幂的除法，乘方，有理数的减法法则计算即可求解 【解答】解：A、2225 2
12、 3，故选项正确； B、252223，故选项错误； C、222543228，故选项错误； D、 （2）（2）（2）8，故选项错误 故选：A 【点评】本题主要考查了负整数指数幂、同底数幂的除法，乘方，有理数的减法法则， 正确对法则进行记忆与理解是解决这类问题的关键 4若 4k5，则 k 的可能值是（ ） A B C2 D 【分析】利用平方法比较数的大小，因为 16k225，将、2、分 别平方即可求解 【解答】解：4k5， 16k225， ， 满足给定的范围， 故选：D 【点评】本题考查无理数的估算；熟练掌握利用平方法比较无理数是解题的关键 5某排球队 6 名场上队员的身高（单位：cm）是：180
13、，184，188，190，192，194现用 一名身高为 186cm 的队员换下场上身高为 192cm 的队员，与换人前相比，场上队员的身 高（ ） A平均数变小，中位数变小 B平均数变小，中位数变大 C平均数变大，中位数变小 D平均数变大，中位数变大 【分析】分别计算出原数据和新数据的平均数和中位数即可得 【解答】解：原数据的平均数为（180+184+188+190+192+194）188，中位数为 189， 新数据的平均数为 （180+184+188+190+186+194） 187， 中位数为187， 所以平均数变小，中位数变小， 故选：A 【点评】本题主要考查中位数和平均数，解题的关键
14、是掌握中位数的定义 6只有 1 和它本身两个因数且大于 1 的自然数叫做素数，我国数学家陈景润在有关素数的 “哥德巴赫猜想”的研究中取得了世界领先的成果若从 5，6，7，9 这 4 个数中随机抽 取一个，则抽到的数是素数的概率是（ ） A B C D1 【分析】四个数中素数为 5 和 7，然后根据概率公式求解 【解答】解：若从 5，6，7，9 这 4 个数中随机抽取一个，则抽到的数是素数的概率 故选：B 【点评】本题考查了概率公式：随机事件 A 的概率 P（A）事件 A 可能出现的结果数除 以所有可能出现的结果数 7下列长度的三条线段能组成锐角三角形的是（ ） A2，3，4 B2，3，5 C3
15、，4，4 D3，4，5 【分析】根据勾股定理求出以较短的两条边为直角边的三角形的斜边的长度，然后与较 长的边进行比较作出判断即可 【解答】解：A、4，2+34，不能组成锐角三角形； B、2+35，不能组成三角形； C、54，3+44，能组成锐角三角形； D、5，是直角三角形，不能组成锐角三角形 故选：C 【点评】本题考查了勾股定理的逆定理，利用勾股定理求出直角三角形的斜边是解题的 关键 8如图，矩形 ABCD 是由三个全等矩形拼成的，AC 与 DE、EF、FG、HG、HB 分别交于 点 P、Q、K、M、N，设EPQ、GKM、BNC 的面积依次为 S1、S2、S3若 S1+S3 30，则 S2的
16、值为（ ） A6 B8 C10 D12 【分析】先证明EPQGKMBNC，再证明AEQAGM 得到， ，所以 S1S2，同理得到 S3S2，所以S2+S230，从而得到 S2的值 【解答】解：矩形 ABCD 是由三个全等矩形拼成， ADEEFGGHB， AEDEGFGBH， DEFFGHHBC， FEHGBC， AQEAMGACB， EPQGKMBNC， QEMG， AEQAGM， ， （）2， S1S2， MGCB， AGMABC， ， （）2， S3S2， S1+S330， S2+S230， S212 故选：D 【点评】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用
17、图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角 形的一般方法是通过作平行线构造相似三角形，灵活运用相似三角形的性质表示线段之 间的关系；也考查了矩形的性质 9如图，一次函数 yx 与反比例函数 y的图象交于 A，B 两点，点 C 在 x 轴上， 连接 AC，BC若ACB90，ABC 的面积为 20，则 k 的值是（ ） A8 B10 C12 D20 【分析】设点 A 为（a，a） ，利用 SACBOC（Ay+|By|）20，构建方程即可 解决问题 【解答】解：设点 A 为（a，a） ， 则 OAa， 点 C 为 x 轴上一点，ACB90，且ACB 的面积为 20，
18、 OAOBOCa， SACBOC（Ay+|By|）（a）（a）20， 解得，a3（舍弃 3） ， 点 A 为（3，4） ， k3412， 故选：C 【点评】本题考查一次函数与反比例函数的交点问题，解题的关键是明确题意，找出所 求问题需要的条件，利用数形结合的思想解答问题 10如图，有两张矩形纸片 ABCD 和 EFGH，ABEF2cm，BCFG8cm把纸片 ABCD 交叉叠放在纸片 EFGH 上，使重叠部分为平行四边形，且点 D 与点 G 重合当两张纸片 交叉所成的角 最小时，sin 等于（ ） A B C D 【分析】 由 “ASA” 可证CDMHDN， 可证 MDDN， 即可证四边形 DN
19、KM 是菱形， 当点 B 与点 E 重合时，两张纸片交叉所成的角 a 最小，由勾股定理求出 MD 的长，即可 得出答案 【解答】解：如图，四边形 ABCD 和四边形 EFGH 是矩形， ADCHDF90，CDAB2cm， CDMNDH，且 CDDH，HC90， CDMHDN（ASA） ， MDND，且四边形 DNKM 是平行四边形， 四边形 DNKM 是菱形， KMMD， sinsinDMC， 当点 B 与点 E 重合时，两张纸片交叉所成的角 a 最小， 设 MDKMacm，则 CM8a（cm） ， MD2CD2+MC2， a24+（8a）2， a（cm） ， sinsinDMC， 故选：B
20、【点评】本题考查了矩形的性质，菱形的判定，勾股定理，全等三角形的判定和性质以 及三角函数定义等知识；求 MD 的长是本题的关键 11如图，AB 是O 的直径，弦 CDAB，DECB若 AB10，CD6，则 DE 的长为 （ ） A B C6 D 【分析】设 AB 与 CD 交于 H，连接 OD，作 OMDE，交 BC 于 N，作 DGBC，根据 垂径定理得出 CHDH，DMEM，BNCN，利用勾股定理求得 OH，即可求得 BH， 进而求得 BC，求得 ON，根据三角形函数求得 DG，因为 MNDG，即可求得 OM，根 据勾股定理求得 DM，得出 DE 【解答】解：设 AB 与 CD 交于 H，
21、连接 OD，作 OMDE，交 BC 于 N，作 DGBC， DEBC， MNBC，DGDE， DGMN， OMDE，ONBC， DMEMDE，BNCN， AB 是O 的直径，弦 CDAB，弦 DECB CHDHCD3， OH4， BH9， BC3， BNBC， ON， sinBCH，即， DG， MNDG， OMMNON， DM， DE2DM 故选：A 【点评】本题考查了垂径定理和勾股定理的应用，作出辅助线构建直角三角形是解题的 关键 12如图，在正方形 ABCD 中，BC2，点 P，Q 均为 AB 边上的动点，BECP，垂足为 E， 则 QD+QE 的最小值为（ ） A2 B3 C D 【分
22、析】作点 D 关于 AB 的对称点 D，连接 DQ，取 BC 的中点 F，连接 EF，过 D作 DG BC 于 G，交 CB 的延长线于 G，当 D，Q，E，F 在同一直线上时，DQ+QE+EF 的最 小值等于DF的长， 此时QD+QE+EF的值最小， 根据勾股定理进行计算， 即可得到QD+QE 的最小值 【解答】解：如图所示，作点 D 关于 AB 的对称点 D，连接 DQ，取 BC 的中点 F，连接 EF， 过 D作 DGBC 于 G，交 CB 的延长线于 G， BECP， RtBCE 中，EFBC1， DGDC2，BGBC2， GF2+13， 当 D， Q， E， F 在同一直线上时， D
23、Q+QE+EF 的最小值等于 DF 的长， 此时 QD+QE+EF 的值最小， RtDGF 中，DF， QD+QE 的最小值为 DFEF1， 故选：D 【点评】本题主要考查了最短距离问题，凡是涉及最短距离的问题，一般要考虑线段的 性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点 二、填空题：本题共二、填空题：本题共 5 小题，满分小题，满分 20 分只要求填写最后结果，每小题填对得分只要求填写最后结果，每小题填对得 4 分分 13计算： 【分析】先化简二次根式、计算乘法，再合并同类二次根式即可得 【解答】解：原式2+35， 故答案为：5 【点评】本题主要考查二次根式的混合运算，
24、解题的关键是掌握二次根式的性质和运算 法则 14运用课本上的计算器进行计算，按键顺序如图，则计算器显示的结果是 1 【分析】根据计算器的按键写出计算的式子然后求值 【解答】解：根据题意得，计算器按键写成算式 （2）3sin30+98+34+31 故答案为：1 【点评】本题考查了科学计算器，熟练了解按键的含义是解题的关键 15在正方形网格中，A、B、C、D、E 均为格点，则BACDAE 45 【分析】根据题意，作出合适的辅助线，然后利用勾股定理的逆定理，可以判断AEF 的形状，从而可以求得BACDAE 的度数 【解答】解：连接 AF、EF， 则CABFAD， FABDAEFAE， BACDAEF
25、AE， 设小正方形的边长为 1， 则 AF，EF，AE， AF2+EF2AE2， AFE 是等腰直角三角形， FAE45， 即BACDAE45， 故答案为：45 【点评】本题考查勾股定理、勾股定理的逆定理，解答本题的关键是明确题意，利用数 形结合的思想解答 16 如图， 过函数 yax2（a0）图象上的点 B，分别向两条坐标轴引垂线， 垂足分别为 A， C线段 AC 与抛物线的交点为 D，则的值为 【分析】设出 OC 的长，表示点 C、B、A 的坐标，进而求出直线 AC 的关系式，再利用 方程组求出交点 D 的横坐标，得出 DE 的长，再利用三角形相似，求出结果 【解答】解：过点 D 作 DE
26、OA，垂足为 E， 设 OCm，则点 C（m，0） ，B（m，am2） ，A（0，am2） ， BCOAam2， 设直线 AC 的关系式为 ykx+b，把 A、C 两点坐标代入得， bam2，kam， yamx+am2， 点 D 的坐标是方程组的一个解， 解这个方程组得，x1m0（舍去） ，x2m， 即：DE|x2|m， 由ADEACO 得， ， 故答案为： 【点评】考查反比例函数、一次函数图象上点的坐标特征，相似三角形、一元二次方程 的应用，综合利用知识，设合适的参数是本题的一个亮点 17如图，在 RtABC 中，C90，AC2，BC4点 M1，N1，P1分别在 AC，BC， AB 上，且四
27、边形 M1CN1P1是正方形，点 M2，N2，P2分别在 P1N1，BN1，BP1上，且四 边形 M2N1N2P2是正方形，点 Mn，Nn，Pn分别在 Pn1Nn1，BNn1，BPn1上，且 四边形 MnNn1NnPn是正方形，则线段 BN2020的长度是 【分析】 根据相似三角形的性质求出 BN1， BN2， BN3的值， 找出规律即可求出线段 BN2020 的长度 【解答】解：N1P1AC， B1N1P1BCA， ， 设 N1P1x，则， 解得：x， BN1BCCN14， 同理， N2P2AC， P1N1BP2N2B， 设 P2N2y， ， 解得：y， BN2 同理，BN3， 线段 BN2
28、020的长度是 故答案为： 【点评】此题考查了相似三角形的性质及正方形的性质，属规律性题目，解答此题的关 键是求出 BN1，BN2，BN3的值，找出规律，根据此规律求解 三、解答题：本大题共三、解答题：本大题共 7 小题，共小题，共 52 分要写出必要的文字说明、证明过程或演算步骤分要写出必要的文字说明、证明过程或演算步骤 18 （5 分）化简：（x+2） 【分析】首先把括号里的式子进行通分，然后把除法运算转化成乘法运算，进行约分化 简 【解答】解：（x+2） （） 故答案为 【点评】分式的四则运算是整式四则运算的进一步发展，在计算时，首先要弄清楚运算 顺序，先去括号，再进行分式的乘除 19
29、（5 分）如图，在ABC 中，A30，B45，AC，求 AB 的长 【分析】过 C 作 CDAB 于 D，求出BCDB，推出 BDCD，根据含 30 度角的直 角三角形求出 CD，根据勾股定理求出 AD，相加即可求出答案 【解答】解： 过 C 作 CDAB 于 D， ADCBDC90， B45， BCDB45， CDBD， A30，AC2， CD， BDCD， 由勾股定理得：AD3， ABAD+BD3+， 答：AB 的长是 3+ 【点评】本题考查了勾股定理，等腰三角形的性质和判定，含 30 度角的直角三角形性质 等知识点的应用，关键是构造直角三角形，题目具有一定的代表性，是一道比较好的题 目
30、20 （8 分）我市某校招聘数学教师，本次招聘进行专业技能笔试和课堂教学展示两个项目 的考核，这两项考核的满分均为 100 分，学校将这两个项目的得分按一定的比例计算出 总成绩经统计，参加考核的 4 名考生的两个项目的得分如下： 考生序号 1 2 3 4 专业技能笔试 90 70 86 75 课堂教学展示 70 90 80 86 （1）经过计算，1 号考生的总成绩为 78 分，求专业技能笔试得分和课堂教学展示得分分 别占总成绩的百分比； （2）若学校录取总成绩最高的考生，通过计算说明 4 名考生中哪一名考生会被录取？ 【分析】 （1）可设专业技能笔试得分占总成绩的百分比是 a，根据 1 号考生
31、的总成绩为 78 分列出方程求解即可； （2）根据加权平均数公式分别求出 4 个考生总成绩，再比较大小即可求解 【解答】解： （1）设专业技能笔试得分占总成绩的百分比是 a 根据题意，得 90a+70（1a）78 解这个方程，得 a40% 140%60% 所以专业技能笔试得分和课堂教学展示得分占总成绩的百分比分别是 40%，60% （2）2 号考生总成绩为 700.4+900.682（分） 3 号考生总成绩为 860.4+800.682.4（分） 4 号考生总成绩为 750.4+860.681.6（分） 因为 82.48281.678，所以 3 号考生会被录取 【点评】本题主要考查加权平均数的
32、计算解题的关键是熟记加权平均数的计算公式 21 （8 分）已知关于 x 的一元二次方程 kx2+（12k）x+k20 （1）若方程有两个不相等的实数根，求 k 的取值范围； （2） 当k取满足 （1） 中条件的最小整数时， 设方程的两根为和， 求代数式3+2+2016 的值 【分析】 （1）根据一元二次方程的定义和判别式的意义得到 k0 且（12k）24k （k2）0，然后求出两不等式的公共部分即可； （2）k1方程变为 x2x10，利用根与系数的关系得到 +1，1，利用 一元二次方程根的定义得到 210，210，则 2+1，32+1，然后 利用整体代入的方法计算 3+2+2016 的值 【解
33、答】解： （1）根据题意得 k0 且（12k）24k（k2）0， 解得 k且 k0； （2）k 取满足（1）中条件的最小整数， k1此时方程变为 x2x10， +1，1， 210，210， 2+1，2+1， 32+1+2+1， 3+2+2016 2+1+1+2016 2（+）+2018 21+2018 2020 【点评】本题考查了根与系数的关系：若 x1，x2是一元二次方程 ax2+bx+c0（a0）的 两根时，x1+x2，x1x2也考查了根的判别式 22 （8 分）在ABCD 中，经过 A、B、C 三点的O 与 AD 相切于点 A，经过点 C 的切线与 AD 的延长线相交于点 P，连接 AC
34、 （1）求证：ABAC； （2）若 AB4，O 的半径为，求 PD 的长 【分析】 （1）连接 AO 并延长交 BC 于点 E，交O 于点 F，根据切线的性质得到FAP 90，证明 AE 是 BC 的垂直平分线，证明结论； （2）连接 FC，OC，设 OEx，根据勾股定理求出 CF，再根据勾股定理列式求出 x，证 明PACABC，根据相似三角形的性质列出比例式，计算即可 【解答】 （1）证明：连接 AO 并延长交 BC 于点 E，交O 于点 F， AP 是O 的切线，AF 是O 的直径， AFAP， FAP90， 四边形 ABCD 是平行四边形， ADBC， AEBFAP90， AFBC， A
35、F 是O 的直径，AFBC， BECE AFBC，BECE， ABAC； （2）解：连接 FC，OC， 设 OEx，则 EFx AF 是O 的直径， ACF90 ACAB4，AF2， 在 RtACF 中，ACF90， CF2 在 RtOEC 中，OEC90， CE2OC2OE2 在 RtFEC 中，FEC90， CE2CF2EF2 OC2OE2CF2EF2，即（）2x222（x）2 解得，x EC， BC2EC 四边形 ABCD 是平行四边形， ADBC， ADBC， PACACB PA，PC 是O 的切线， PAPC PACPCA ABAC， ABCACB PACABC，PCAACB， PA
36、CABC， APAB2 PDAPAD 【点评】本题考查的是切线的性质、相似三角形的判定和性质，掌握圆的切线垂直于经 过切点的半径是解题的关键 23 （9 分）已知在 RtABC 中，ABC90，ABBC，将ABC 绕点 A 逆时针方向旋 转，得到ADE，旋转角为 （090） ，直线 BD 与 CE 交于点 F （1）如图 1，当 45时，求证：CFEF； （2）如图 2，在旋转过程中，当 为任意锐角时， CFB 的度数是否变化？若不变，请求出它的度数； 结论“CFEF” ，是否仍然成立？请说明理由 【分析】 （1）先判断出BACBCA45，借助旋转求出ABDADB67.5， 进而判断出 CFD
37、F，再判断出CEDEDF 得出 EFDF，即可得出结论； （2）先判断出ABDACE，再用三角形内角和定理即可得出结论； 先判断出 ADAB，得出ABDADB，进而得出EDGCBF，再判断出 EG ED，进而判断出FEGFCB（AAS） ，即可得出结论 【解答】解： （1）当 45时，在 RtABC 中，ABC90，ABBC， BACBCA45， 由旋转知，AEDACB45，ADEABC90，ABAD， ABDADB67.5， CDFADB67.5， 同理，ACE67.5， ACECDF67.5， CFDF， 在 RtCDE 中，CEDAECAED22.5，EDFCDECDF90 67.522
38、.5， CEDEDF， EFDF， CFEF； （2）CFB 的度数不变，CFB45， 理由：如图 2，由旋转知，ADAB，AEAC，BADCAE， ABD 与ACE 均为顶角为 的等腰三角形， 底角相等， 即ABDACE， 设 AC 与 BF 的交点为 O，则AOBCOF， ABD+AOB+CABACE+COF+CFB180， CFBCAB45； 结论“CFEF” ，仍然成立 理由：如图 2，作 EGCB 交 BF 延长线于点 G， 由旋转知 DEBC，ADEABC90，ADAB， ABDADB， 又ADE90， EDG+ADBCBF+ABD90， EDGCBF， EGCB， GCBFEDG
39、， EGED， 又EDBC， EGBC， FEGFCB（AAS） ， EFCF 【点评】此题是几何变换综合题，主要考查了等腰直角三角形的性质，旋转的性质，三 角形的内角和定理，平行线的性质，全等三角形的判定和性质，等腰三角形的性质，判 断出ABDACE 是解本题的关键 24 （9 分）如图，在平面直角坐标系中，直线 ykx7 与 y 轴交于点 C，与 x 轴交于点 B， 抛物线 yax2+bx+14a 经过 B、C 两点，与 x 轴的正半轴交于另一点 A，且 OA：OC2： 7 （1）求抛物线的解析式； （2）点 D 在线段 CB 上，点 P 在对称轴的左侧抛物线上，PDPB，当 tanPDB
40、2， 求点 P 的坐标； （3）在（2）的条件下，点 Q（7，n）在第四象限，点 R 在对称轴的右侧抛物线上，若 以点 P、D、Q、R 为顶点的四边形为平行四边形，求点 Q、R 的坐标 【分析】 （1）由直线可求得 C 点坐标，代入抛物线可求得 a 的值，结合条件可求得 A 点 坐标，代入可求得 b 的值，可求得抛物线解析式； （2）可先求得 B 点坐标，过 P 作 PFx 轴于点 G，交 BC 于点 F，作 PEBC，结合条 件可找到 PG 与 GF 关系，再求得直线 BC 的解析式，设出 F 点的坐标，可表示出 P 点坐 标，代入抛物线可求得 P 点的坐标； （3）分两种情形 DPQR 和
41、 DRQP 求解，当 DPQR 时，过 P 作 PNBQ，过 D 作 DNBQ 交 PN 于点 N，过 R 作 RMBQ 于点 M设 PD 交 BQ 于点 T，DN 交 BM 于点 I，可求得 RMDN，MQPN，结合条件可求得 D 点坐标，设出 R 的坐标，可求得横坐 标，代入抛物线可求得 R 的坐标，再根据平行四边形的性质可求得 Q 的坐标；同理可求 得当 DRQP 时的 R、Q 的坐标 【解答】解： （1）直线 ykx7 与 y 轴的负半轴交于点 C C（0，7） ， OC7， 抛物线 yax2+bx+14a 经过点 C， 14a7， a， yx2+bx7， OA：OC2：7 OA2，
42、A（2，0） 抛物线 yx2+bx7 经过点 A， b 抛物线的解析式为 yx2+x7， （2）如图 1， 抛物线 yx2+x7 经过 B 点， 令 y0 解得 x7 或 x2（舍去） ， B（7，0） ， OB7， OCOB， OCBOBC45 过点 P 作 PFx 轴于点 G，交 CB 延长线于点 F，则 PFy 轴， CFGOCB45， BFGF， 过 P 作 PEBC 于点 E， PDPB， PBDPDB， tanPBDtanPDB2， PE2BE， EFPE， BFBE， PFPE2 BE2 BF4GF， PG3GF， 直线 ykx7 过 B 点， k1， yx7， 设 F（m，m7
43、） ，则 P（m，3（m7） ） ， 点 P 在抛物线 yx2+x7 上， 3（m7）m2+m7， 解得 m7（舍去）或 m8， P（8，3） ； （3）如图 2，当 DPQR 时，即四边形 DQRP 是平行四边形， B（7，0） ，Q（7，m） BQy 轴 过 P 作 PNBQ，过 D 作 DNBQ 交 PN 于点 N， 过 R 作 RMBQ 于点 M 设 PD 交 BQ 于点 T，DN 交 BM 于点 I， DTBDPN，PTQRQM， DTBPTQ， DPNRQM， 四边形 DPRQ 是平行四边形， DPRQ， 在RMQ 和DNP 中， ， RMQDNP（AAS） ， RMDN，MQPN
44、， 由（2）可求 F（8，1） ，GF1，BD2BE2BF2 GF2 ， QBC45，BIDI2， D（5，2） ， 设 R 点的横坐标为 t， RMDN， t785， 解得 t10， 点 R 在抛物线 yx2+x7 上， 当 t10 时，102+10712， R（10，12） ， MQPN， 3212n， n11， R（10，12） ，Q（7，11） ， 如图 3，当 DRQP 时，即四边形 DQPR 是平行四边形 同理可求得 R（6，2） ，Q（7，7） 【点评】本题考查二次函数综合题、一次函数的应用、待定系数法、全等三角形的判定 和性质、锐角三角函数、平行四边形的判定和性质等知识，解题的关键是灵活运用所学 知识解决问题，学会用分类讨论的思想思考问题，属于中考压轴题
