 湖北省武汉市江夏区2020年中考模拟数学试卷(一)含答案
湖北省武汉市江夏区2020年中考模拟数学试卷(一)含答案
《湖北省武汉市江夏区2020年中考模拟数学试卷(一)含答案》由会员分享,可在线阅读,更多相关《湖北省武汉市江夏区2020年中考模拟数学试卷(一)含答案(11页珍藏版)》请在七七文库上搜索。
1、江夏区 20192020 学年度九年级中考模拟测试(一) 数 学 试 卷 (考试时间: 120 分钟 试卷满分:120 分) 江夏区教研室 2020 届九年级数学中心组 一、选择题(每小题一、选择题(每小题 3 分,共分,共 30 分)分) 1.有理数3 的相反数是( ) A.3 B. 3 C. 1 3 D. 1 3 2.式子 x2在实数范围内有意义,则 x 的取值范腾是( ) A. x0 B. x2 C. x2 D. x2 3.不透明的袋子中装有形状、大小、质地完全相同的 5 个球,其中 3 个黑球、2 个白球, 从袋子中一次摸出 3 个球,下列事件是不可能事件的是( ) A.摸出的是 2
2、个白球、1 个黑球 B.摸出的是 3 个黑球 C.摸出的是 3 个白球 D.摸出的是 2 个黑球、1 个白球 4.下列图形中,既是中心对称图又是轴对称图形的是( ) A. B. C. D. 5.如图是由 5 个完全相同的小正方体搭成的儿何体,如果将小正方体 A 放到 小正方体 B 的正上方,则它的( ) A.主视图会发生改变 B.俯视图会发生改变 C.左视图会发生改变 D.三种视图都会发生改变 6.如图,矩形 ABCD 中,AB2,BC3,动点 P 沿折线 BCD 从点 B 开 始运动到点 D. 设运动的路程为 x,ADP 的面积为 y,那么 y 与 x 之 间的函数关系的图象大致是( ) A
3、. B. C. D. 7.投掷枚质地均匀的骰子两次,向上一面的点数依次记为 a、b. 那么方程 x2axb0 有解的概 率是( ) A.1 2 B. 1 3 C. 8 15 D. 19 36 8. 如图,平面直角坐标系中,点 B 在第一象限,BAx 轴于点 A,反比例 函数 yk x(x0)的图象经过线段 AB 的中点 C,点 C 关于直线 yx 的 对称点 C的坐标为(1,n),若OAB 的面积为 3,则 n 的值为( ) A. 1 3 B. 1 C. 2 D. 3 9. 有一列数:a1、a2,a3,an;其中 a10,a42,若 aiai1ai2 (i1,i 为正整数) , 则 a7( )
4、 A.5 B.8 C.10 D.13 10. 如图,四边形 ABCD 内接于O,AECB 交 CB 的延长线于点 E, 若 BA 平分DBE,AE3 5,CD8,sinADB3 4,则O 的 E CB O A D 半径为( ) A. 4.5 B.2 5 C. 5 D.4 5 二、填空题(每小题二、填空题(每小题 3 分,共分,共 18 分)分) 11.计算 12的结果是_. 12.有一组数:3,5,2,7,3,这组数的中位数为_. 13.计算: 4 x24x 1 x4_. 14.如图,在ABC 中,ABAC,点 D、E 分别在边 BC、AB 上, 且 ADAE,CAD32, 则BDE_. 15
5、.抛物线 yax2bxc (a、b、c 为常数)经过点 A (1,0)、B(m,0)、C(2,n)(1m3,n0, 下列结论:abc0;3ac0,若 P (n,t)为抛物线上任一点,则(m1 2 )a(m1 2 )ban2 bn,当 a1 时,则 b 的取值范围为 0b2. 其中正确结论的序号为_. 16. 如图,在ABC 中,AB5,D 为边 AB 上动点,以 CD 为一边作正方形 CDEF, 当点 D 从点 B 运动到点 A 时,点 E 运动的路径长为_. 三、解答题(共三、解答题(共 8 题,共题,共 72 分)分) 17.(8 分)计算:x3x3x5x(2x2)2. 18.(8 分)如
6、图,直线 EF 分别交 AB、CD 于 G、H,BGH、DHF 的 平分线分别为 GM、HN,且 GMHN. 求证:ABCD. 19.(8 分)某校为了解学生对垃圾分类知识的掌握情况, 在校园内随机抽取了部分学生进行问卷调查, 将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表 和条形统计图. 请根据图表信息, 解答下列问题: (1)本次调查随机抽取了_名学生, 表中,m_,n_; (2)补全条形统计图; (3)若全校有 2000 名学生,请估计该校 掌握垃圾分类知识达到“优秀”和 “良好”等级的学生共有多少人? 等级 频数 频率 优秀 21 42% 良好 m
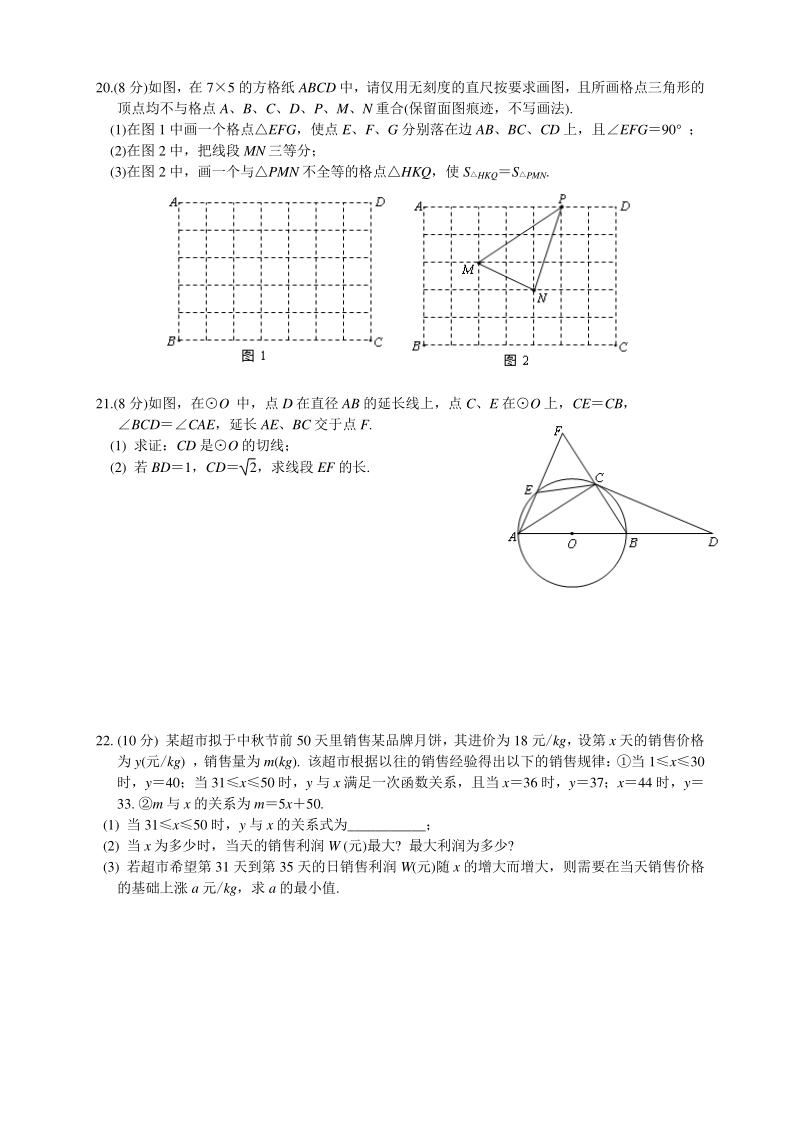
7、40% 合格 6 n% 不合格 3 6% 20.(8 分)如图,在 75 的方格纸 ABCD 中,请仅用无刻度的直尺按要求画图,且所画格点三角形的 顶点均不与格点 A、B、C、D、P、M、N 重合(保留面图痕迹,不写画法). (1)在图 1 中画一个格点EFG,使点 E、F、G 分别落在边 AB、BC、CD 上,且EFG90 ; (2)在图 2 中,把线段 MN 三等分; (3)在图 2 中,画一个与PMN 不全等的格点HKQ,使 SHKQSPMN. 21.(8 分)如图,在O 中,点 D 在直径 AB 的延长线上,点 C、E 在O 上,CECB, BCDCAE,延长 AE、BC 交于点 F.
8、 (1) 求证:CD 是O 的切线; (2) 若 BD1,CD 2,求线段 EF 的长. 22. (10 分) 某超市拟于中秋节前 50 天里销售某品牌月饼, 其进价为 18 元/kg, 设第 x 天的销售价格 为 y(元/kg) , 销售量为 m(kg). 该超市根据以往的销售经验得出以下的销售规律: 当 1x30 时,y40;当 31x50 时,y 与 x 满足一次函数关系,且当 x36 时,y37;x44 时,y 33. m 与 x 的关系为 m5x50. (1) 当 31x50 时,y 与 x 的关系式为_; (2) 当 x 为多少时,当天的销售利润 W (元)最大? 最大利润为多少?
9、 (3) 若超市希望第 31 天到第 35 天的日销售利润 W(元)随 x 的增大而增大,则需要在当天销售价格 的基础上涨 a 元/kg,求 a 的最小值. 23.(10 分)矩形 ABCD 中,动点 E、F 分别在边 AB、AD 上,FGDE 于 H 交直线 BC 于 G. (1) 如图 1,求证:FG DE AB AD; (2) 如图 2,若 AB6,AD9,点 E 为 AB 中点,当 tanHEGl 时,求 AF 的长; (3) 如图 3,若 AB4,AD6,AB4BE,当 tanHEG5 7 时,直接写出 AF 的长. 24. (12 分)已知抛物线 yax2bxc 的顶点为 D (6
10、 5, 14 5 ),经过点 C (0,1), 且与 x 轴交于 A、B 两点(A 在 B 的左侧). (1) 求抛物线的解析式: (2) P 为抛物线上一点,连 CP 交 OD 于点 Q,若 SCOQSPDQ,求 P 点的横坐标; (3)点 M 为直线 BC 下方抛物线上一点,过 M 的直线与 x 轴、y 轴分别交于 E、F, 且与抛物线有且只有一个公共点. 若FCMOEF,求点 M 的坐标. 江夏区 20192020 学年度九年级中考模拟测试(一) 数 学 试 卷 (考试时间: 120 分钟 试卷满分:120 分) 江夏区教研室 2020 届九年级数学中心组 一、选一、选择择题题(每小题每
11、小题 3 分,共分,共 30 分分) 1.有理数3 的相反数是( ) A.3 B. 3 C. 1 3 D. 1 3 【答案】A. 2.式子 x2在实数范围内有意义,则 x 的取值范腾是( ) A. x0 B. x2 C. x2 D. x2 【答案】B. 3.不透明的袋子中装有形状、大小、质地完全相同的 5 个球,其中 3 个黑球、2 个白球, 从袋子中一次摸出 3 个球,下列事件是不可能事件的是( ) A.摸出的是 2 个白球、1 个黑球 B.摸出的是 3 个黑球 C.摸出的是 3 个白球 D.摸出的是 2 个黑球、1 个白球 【答案】C. 4.下列图形中,既是中心对称图又是轴对称图形的是(
12、) A. B. C. D. 【答案】D. 5.如图是由 5 个完全相同的小正方体搭成的儿何体,如果将小正方体 A 放到 小正方体 B 的正上方,则它的( ) A.主视图会发生改变 B.俯视图会发生改变 C.左视图会发生改变 D.三种视图都会发生改变 【答案】A. 6.如图,矩形 ABCD 中,AB2,BC3,动点 P 沿折线 BCD 从点 B 开 始运动到点 D. 设运动的路程为 x,ADP 的面积为 y,那么 y 与 x 之 间的函数关系的图象大致是( ) A. B. C. D. 【答案】D. 7.投掷枚质地均匀的骰子两次,向上一面的点数依次记为 a、b. 那么方程 x2axb0 有解的概
13、率是( ) A.1 2 B. 1 3 C. 8 15 D. 19 36 【答案】D. 一次投掷骰子,向上的点数有 6 种,两次投掷则有 6636 种。 则 a1、2、3、5 或 6,b1、2、3. 4、5 或 6. 一元二次方程有解,则a24b0. 当 a1 时,有 0 种; 当 a2 时,b1,有 1 种;当 a3 时,b1 或 2,有 2 种; 当 a4 时,b1、 2、3 或 4 有 4 种;当 a5 时,b1、2、3、4、5 或 6 ,有 6 种; 当 a6 时, b1、2、3、4、5 或 6 也有 6 种。 共有 1246619 种。 故选 D. 8. 如图,平面直角坐标系中,点 B
14、 在第一象限,BAx 轴于点 A,反比例 函数 yk x(x0)的图象经过线段 AB 的中点 C,点 C 关于直线 yx 的 对称点 C的坐标为(1,n),若OAB 的面积为 3,则 n 的值为( ) A. 1 3 B. 1 C. 2 D. 3 【答案】D. 由 C (1,n)可知 C(n,1),A(n,0),B(n,2),SOAB1 2OAAB3, 得:OAAB6,2n6,n3. 9. 有一列数:a1、a2,a3,an;其中 a10,a42,若 aiai1ai2 (i1,i 为正整数) , 则 a7( ) A.5 B.8 C.10 D.13 【答案】B. aiai1ai2,a1a2a3,a1


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 湖北省 武汉市 江夏区 2020 年中 模拟 数学试卷 答案
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
文档标签
- 数学试卷
- 武汉市蔡甸区汉阳一中
- 武汉市江夏区第一中学
- 湖北省武汉市洪山区
- 武汉市梅学校20202021学年度上学期十二月八年级数学试卷
- 华东师大2021最新中考模拟示范卷数学三山西
- 武汉市江夏区求实中学
- 湖北省武汉市江夏区庙山小学
- 湖北省武汉市洪山区2020年中考模拟语文试卷一含答案
- 湖北省武汉市武昌区2019年中考数学训练试题一含答案
- 湖北省武汉市2020年中考模拟数学试卷三含答案
- 广西省苍梧县2019年中考模拟数学试卷一含答案
- 2021年5月湖北省武汉市江夏区中考数学模拟试卷含答案详解
- 湖北省武汉市江夏区2020年中考模拟数学试卷一含答案
- 湖北省武汉市2020年中考数学评价检测试卷三含答案
- 湖北省武汉市2020年中考道德与法治试卷含答案解析
- 2020年6月湖北省武汉市部分学校中考模拟数学试卷含答案
- 湖北省武汉市2020年中考数学逼真模拟试卷一含答案解析
- 湖北省荆州市2020年中考数学试卷含答案



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-147943.html