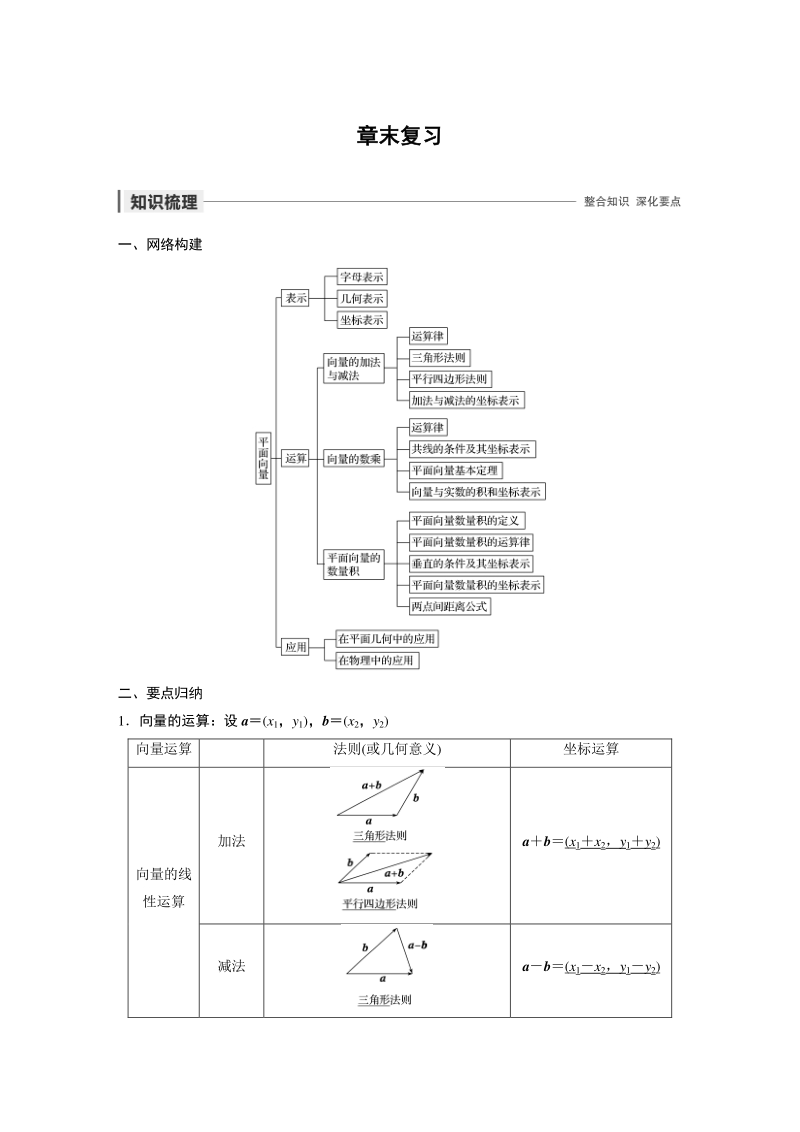
1、章末复习章末复习 一、网络构建 二、要点归纳 1向量的运算：设 a(x1，y1)，b(x2，y2) 向量运算 法则(或几何意义) 坐标运算 向量的线 性运算 加法 ab(x1x2，y1y2) 减法 ab(x1x2，y1y2) 数乘 (1)|a|a|； (2)当 0 时，a 的方向与 a 的方向相 同；当 0) (1)用 k 表示数量积 a b； (2)求 a b 的最小值，并求出此时 a 与 b 的夹角 的大小 考点 数形结合思想在向量问题中的应用 题点 数形结合思想在向量问题中的应用 解 (1)由|kab| 3|akb|， 得(kab)23(akb)2， k2a22ka bb23a26ka
2、b3k2b2. (k23)a28ka b(13k2)b20. |a|cos2sin21，|b| cos2sin21， k238ka b13k20， a b2k 22 8k k 21 4k (k0) (2)a bk 21 4k 1 4 k1 k . 由对勾函数的单调性可知，f(k)1 4 k1 k 在(0,1上单调递减，在1，)上单调递增， 当 k1 时，f(k)minf(1)1 4(11) 1 2， 此时 a 与 b 的夹角 的余弦值 cos a b |a|b| 1 2， 又0 180 ，60 . 反思感悟 数量积运算是向量运算的核心，利用向量数量积可以解决以下问题： (1)设 a(x1，y1
3、)，b(x2，y2)， abx1y2x2y10， abx1x2y1y20. (2)求向量的夹角和模的问题 设 a(x1，y1)，则|a| x21y21. 两向量夹角的余弦值(0，a，b 为非零向量) cos a b |a|b| x1x2y1y2 x21y21 x22y22 . 跟踪训练 2 已知ABC 是边长为 1 的等边三角形，点 D，E 分别是边 AB，BC 的中点，连 接 DE 并延长到点 F，使得 DE2EF，则AF BC的值为( ) A5 8 B. 1 8 C. 1 4 D. 11 8 考点 基底思想在解题中的应用 题点 基底思想在解题中的应用 答案 B 解析 BC ACAB，AFA
4、D DF 1 2AB 3 2DE 1 2AB 3 4AC ， BC AF(ACAB) 1 2AB 3 4AC 1 211 1 2 1 2 3 4 3 411 1 2 1 4 3 4 1 2 3 8 1 8. 题型三 向量坐标法在平面几何中的应用 例 3 在 RtABC 中，CACB2，M，N 是斜边 AB 上的两个动点，且 MN 2，则CM CN 的取值范围为_ 考点 向量坐标在解题中的应用 题点 向量坐标在解题中的应用 答案 3 2，2 解析 以 C 为坐标原点，CA 所在直线为 x 轴，CB 所在直线为 y 轴，建立平面直角坐标系(如 图所示)， 则 C(0,0)，A(2,0)，B(0,2
5、)，所以直线 AB 的方程为 xy20. 设 M(t，2t)，则 N(t1，1t)(0t1)， 所以CM CN t(t1)(2t)(1t)2t22t22 t1 2 23 2. 因为 0t1，所以CM CN 的取值范围为 3 2，2 . 反思感悟 把几何图形放到适当的坐标系中，就赋予了有关点与向量具体的坐标，这样就能 进行相应的代数运算和向量运算，从而解决问题这样的解题方法具有普遍性 跟踪训练 3 如图， 半径为 3的扇形 AOB 的圆心角为 120 ， 点 C 在AB上， 且COB30 ， 若OC OA OB ，则 等于( ) A. 3 B. 3 3 C.4 3 3 D2 3 考点 向量坐标在
6、解题中的应用 题点 向量坐标在解题中的应用 答案 A 解析 由题意，得AOC90 ，故以 O 为坐标原点，OC，OA 所在直线分别为 x 轴，y 轴建 立平面直角坐标系， 则 O(0,0)，A(0， 3)，C( 3，0)，B( 3cos 30 ， 3sin 30 )， 因为OC OA OB ， 所以( 3，0)(0， 3) 3 3 2 ， 31 2 ， 即 3 3 3 2 ， 0 3 31 2， 则 2 3 3 ， 3 3 ， 所以 3. 1在菱形 ABCD 中，若 AC2，则CA AB等于( ) A2 B2 C|AB |cos A D与菱形的边长有关 答案 B 解析 如图，设对角线 AC 与
7、 BD 交于点 O，AB AO OB . CA ABCA (AO OB ) 202. 2已知|a|1，a b1 2，|ab| 21，则 a 与 b 的夹角等于( ) A30 B45 C60 D120 考点 平面向量数量积的应用 题点 利用数量积求向量的夹角 答案 C 解析 设 a 与 b 的夹角为 ， 因为 a b|a|b| cos 1 2，且|a|1， 所以|b|cos 1 2. 又|ab|2|a|2|b|22a b1， 即 1|b|211， 故|b|1. 由得 cos 1 2. 又 0 180 ，所以 60 ，故选 C. 3已知向量 a(1， 3)，b(3，m)若向量 a，b 的夹角为 6
8、，则实数 m 等于( ) A2 3 B. 3 C0 D 3 答案 B 解析 a b(1， 3) (3，m)3 3m， a b12 32 32m2cos 6， 3 3m12 3232m2cos 6， m 3. 4已知向量 a(1,2)，b(2，3)若向量 c 满足(ca)b，c(ab)，则 c_. 考点 向量坐标在解题中的应用 题点 向量坐标在解题中的应用 答案 7 9， 7 3 解析 设 c(x，y)，则 ca(x1，y2) 又(ca)b，2(y2)3(x1)0. 又 c(ab)， (x，y) (3，1)3xy0. 联立解得 x7 9，y 7 3. 5 平面向量 a( 3， 1)， b 1 2， 3 2 ， 若存在不同时为 0 的实数 k 和 t， 使 xa(t23)b， ykatb，且 xy，试求函数关系式 kf(t) 考点 向量坐标在解题中的应用 题点 向量坐标在解题中的应用 解 由 a( 3，1)，b 1 2， 3 2 ， 得 a b0，|a|2，|b|1， 由 xy，得a(t23)b (katb)0， ka2ta bk(t23)a bt(t23)b20， 4kt33t0，k1 4(t 33t)，f(t)1 4(t 33t)， 所以函数关系式为 kf(t)1 4(t 33t)
