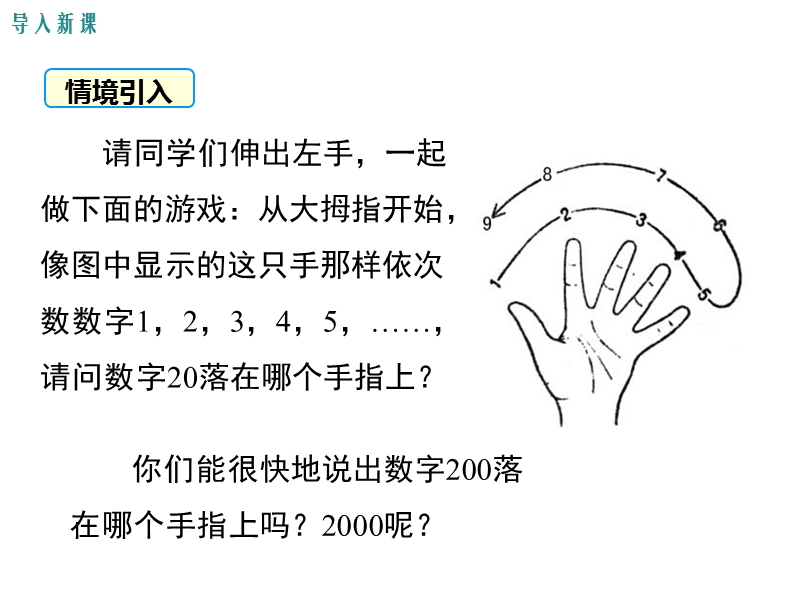
1、,导入新课,讲授新课,当堂练习,课堂小结,5 探索与表达规律,第三章 整式及其加减,学习目标,1.能用代数式表示数与图形的变化规律.(重点） 2.进一步培养学生观察、分析、抽象、概括等思维能力和应用意识.（难点）,导入新课,情境引入,请同学们伸出左手，一起做下面的游戏：从大拇指开始，像图中显示的这只手那样依次数数字1，2，3，4，5，请问数字20落在哪个手指上？,你们能很快地说出数字200落在哪个手指上吗？2000呢？,讲授新课,合作探究,请同学们认真观察日历表，回答下列问题：,(1)请找出同一横线上三个相邻数之间的关系： (2)请同学们找一找竖列三个相邻数的关系； (3)请同学们找一找左上右
2、下对角线上三个相邻数的关系； (4)请同学们找一找左下右上对角线上三个相邻数的关系.,绿色方框中的九个数之和与该方框正中间的数有什么关系？,绿色方框中九个数之和=9正中间的数,猜想:,a,a-7,a+8,a-8,a+6,a-6,a+7,a-1,a+1,(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)+(a+6)+(a+7) +(a+8) = _,9a,结论:绿色方框中九个数之和=9正中间的数,用代数式表示,做一做,十字形中的数字有何规律？你是如何验证的？,规律: 十字形中五数之和=5中间数,规律: “H”形中七数之和=7中间数,“H”形中的数字有何规律？你是如何验证的？,你还能设
3、计其他形状的包含数字规律的数框吗？,探索规律的一般步骤：,猜 想 规 律,表 示 规 律,验 证 规 律,具 体 问 题,观察、比较,成立,得出结论,归纳,议一议,观察下列等式，找出规律填空：,典例精析,方法归纳,用代数式表示数的变化的规律： （1）数字为整数，考虑相邻两数的和、差、积、商、符号等方面是否存在规律，也可以是奇、偶、平方等方面的规律; （2）数字为分数，可分别观察分子、分母的变化规律及它们之间的联系； （3）若表示数字变化规律的是等式（或表格），可将每个等式对应写好，然后比较每一行每一列数字之间的关系，从而找出规律.,练一练,正整数按下图的规律排列，则第20行，第21列的数字是_
4、.,380,49,练一练,观察下列图形，则第n个图形中三角形的个数是( ),A2n2 B4n4 C4n4 D4n,D,例3 将棱长为1的正方体层层叠放如图所示，问第(5)个、第(6)个图形各需多少个正方体？,解析 认真观察图形，注意分析看不到的地方，再从中找出规律,解：第(5)个图形需1(12)(123)(1234)(12345)35(个)正方体同理，第(6)个图形需56个正方体,练一练,如图，用灰、白两色正方形瓷砖铺设地面，第n个图案中白色瓷砖有_块,(3n2),解析 观察第1个图案中白色瓷砖的块数为1315，第2个图案中白色瓷砖的块数为2428，第3个图案中白色瓷砖的块数为35311，依此规律可以得到第n个图案中白色瓷砖的块数为n(n2)n3n2.,当堂练习,C,64x7,606,4.观察下列等式: 32-12=42； 42-22=43； 52-32=44； （ ）2 -（ ）2=（ ）（ ）； 填写第4个等式，第n个等式为_ .,6,4,4,5,课堂小结,探索与表达规律,
