1、2020 年湖南省常德市中考数学试卷年湖南省常德市中考数学试卷 一选择题（共一选择题（共 8 小题）小题） 14 的倒数为（ ） A B2 C1 D4 2下面几种中式窗户图形既是轴对称又是中心对称的是（ ） A B C D 3如图，已知 ABDE，130，235，则BCE 的度数为（ ） A70 B65 C35 D5 4下列计算正确的是（ ） Aa2+b2（a+b）2 Ba2+a4a6 Ca10a5a2 Da2a3a5 5下列说法正确的是（ ） A明天的降水概率为 80%，则明天 80%的时间下雨，20%的时间不下雨 B抛掷一枚质地均匀的硬币两次，必有一次正面朝上 C了解一批花炮的燃放质量，应
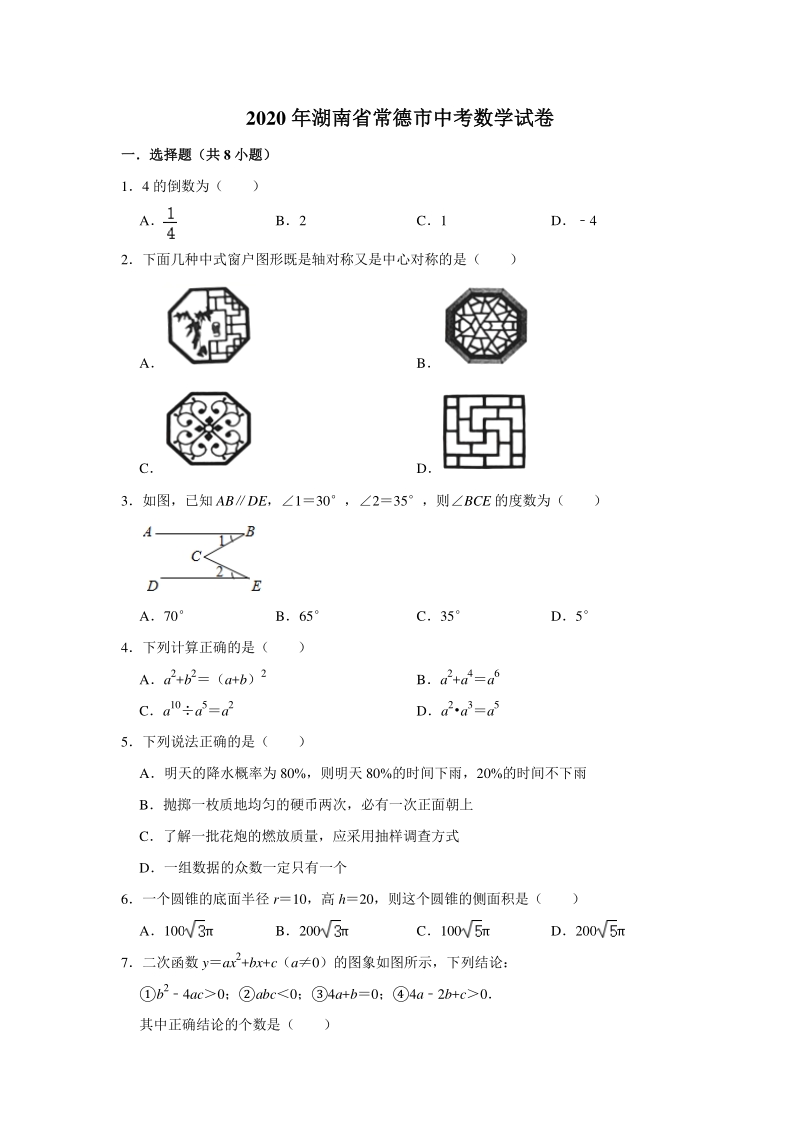
2、采用抽样调查方式 D一组数据的众数一定只有一个 6一个圆锥的底面半径 r10，高 h20，则这个圆锥的侧面积是（ ） A100 B200 C100 D200 7二次函数 yax2+bx+c（a0）的图象如图所示，下列结论： b24ac0；abc0；4a+b0；4a2b+c0 其中正确结论的个数是（ ） A4 B3 C2 D1 8如图，将一枚跳棋放在七边形 ABCDEFG 的顶点 A 处，按顺时针方向移动这枚跳棋 2020 次移动规则是：第 k 次移动 k 个顶点（如第一次移动 1 个顶点，跳棋停留在 B 处，第 二次移动 2 个顶点，跳棋停留在 D 处） ，按这样的规则，在这 2020 次移动
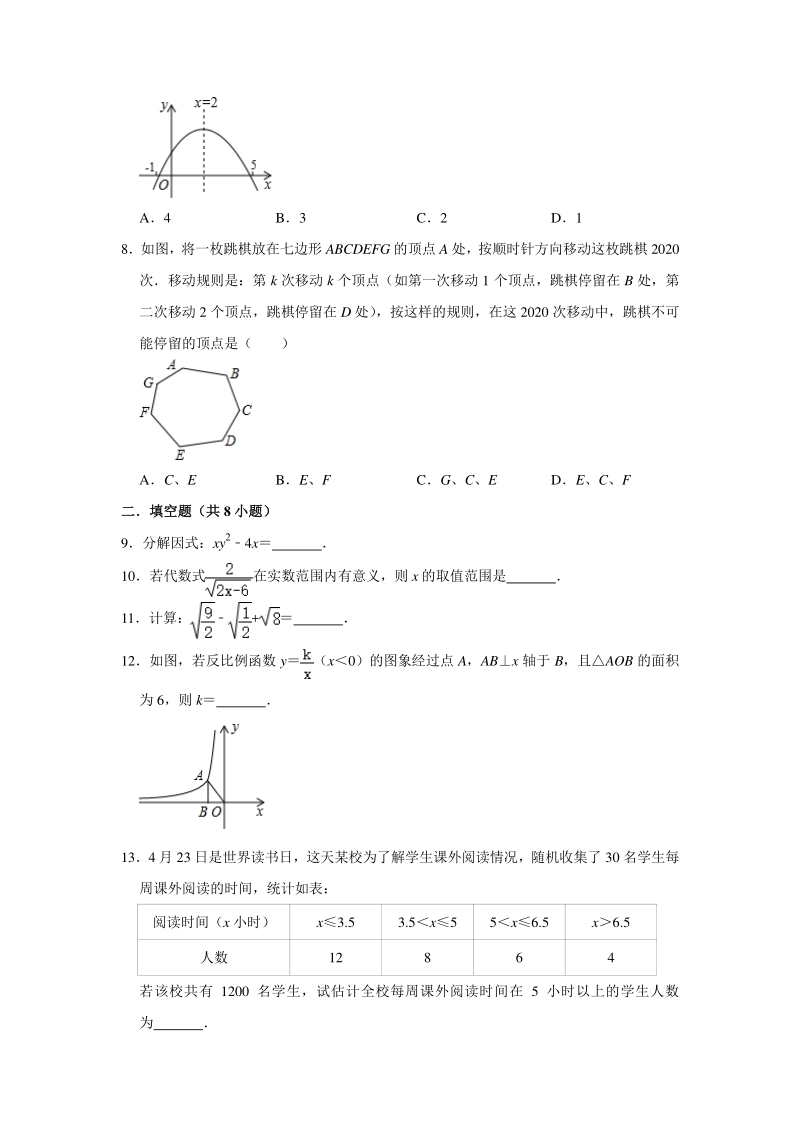
3、中，跳棋不可 能停留的顶点是（ ） AC、E BE、F CG、C、E DE、C、F 二填空题（共二填空题（共 8 小题）小题） 9分解因式：xy24x 10若代数式在实数范围内有意义，则 x 的取值范围是 11计算：+ 12如图，若反比例函数 y（x0）的图象经过点 A，ABx 轴于 B，且AOB 的面积 为 6，则 k 134 月 23 日是世界读书日，这天某校为了解学生课外阅读情况，随机收集了 30 名学生每 周课外阅读的时间，统计如表： 阅读时间（x 小时） x3.5 3.5x5 5x6.5 x6.5 人数 12 8 6 4 若该校共有 1200 名学生，试估计全校每周课外阅读时间在 5
4、 小时以上的学生人数 为 14今年新冠病毒疫情初期，口罩供应短缺，某地规定：每人每次限购 5 只李红出门买口 罩时，无论是否买到，都会消耗家里库存的口罩一只，如果有口罩买，他将买回 5 只已 知李红家原有库存 15 只，出门 10 次购买后，家里现有口罩 35 只请问李红出门没有买 到口罩的次数是 次 15如图 1，已知四边形 ABCD 是正方形，将DAE，DCF 分别沿 DE，DF 向内折叠得 到图2， 此时DA与DC重合 （A、 C都落在G点） ， 若GF4， EG6， 则DG的长为 16阅读理解：对于 x3（n2+1）x+n 这类特殊的代数式可以按下面的方法分解因式： x3（n2+1）x
5、+nx3n2xx+nx（x2n2）（xn）x（xn） （x+n）（xn） （xn） （x2+nx1） 理解运用：如果 x3（n2+1）x+n0，那么（xn） （x2+nx1）0，即有 xn0 或 x2+nx10， 因此，方程 xn0 和 x2+nx10 的所有解就是方程 x3（n2+1）x+n0 的解 解决问题：求方程 x35x+20 的解为 三解答题（共三解答题（共 10 小题）小题） 17计算：20+（） 1 4tan45 18解不等式组 19先化简，再选一个合适的数代入求值： （x+1） 20第 5 代移动通信技术简称 5G，某地已开通 5G 业务，经测试 5G 下载速度是 4G 下载速
6、 度的 15 倍，小明和小强分别用 5G 与 4G 下载一部 600 兆的公益片，小明比小强所用的 时间快 140 秒，求该地 4G 与 5G 的下载速度分别是每秒多少兆？ 21已知一次函数 ykx+b（k0）的图象经过 A（3，18）和 B（2，8）两点 （1）求一次函数的解析式； （2）若一次函数 ykx+b（k0）的图象与反比例函数 y（m0）的图象只有一个 交点，求交点坐标 22如图 1 是自动卸货汽车卸货时的状态图，图 2 是其示意图汽车的车厢采用液压机构、 车厢的支撑顶杆 BC 的底部支撑点 B 在水平线 AD 的下方，AB 与水平线 AD 之间的夹角 是 5，卸货时，车厢与水平线
7、 AD 成 60，此时 AB 与支撑顶杆 BC 的夹角为 45，若 AC 2米 ， 求BC的 长度 （ 结果 保 留一 位 小数 ） （参考数据：sin650.91，cos650.42，tan652.14，sin700.94，cos70 0.34，tan702.75，1.41） 23今年 24 月某市出现了 200 名新冠肺炎患者，市委根据党中央的决定，对患者进行了 免费治疗图 1 是该市轻症、重症、危重症三类患者的人数分布统计图（不完整） ，图 2 是这三类患者的人均治疗费用统计图请回答下列问题 （1）轻症患者的人数是多少？ （2）该市为治疗危重症患者共花费多少万元？ （3）所有患者的平均治
8、疗费用是多少万元？ （4）由于部分轻症患者康复出院，为减少病房拥挤，拟对某病房中的 A、B、C、D、E 五位患者任选两位转入另一病房，请用树状图法或列表法求出恰好选中 B、D 两位患者 的概率 24如图，已知 AB 是O 的直径，C 是O 上的一点，D 是 AB 上的一点，DEAB 于 D， DE 交 BC 于 F，且 EFEC （1）求证：EC 是O 的切线； （2）若 BD4，BC8，圆的半径 OB5，求切线 EC 的长 25如图，已知抛物线 yax2过点 A（3，） （1）求抛物线的解析式； （2）已知直线 l 过点 A，M（，0）且与抛物线交于另一点 B，与 y 轴交于点 C，求证：
9、MC2MAMB； （3）若点 P，D 分别是抛物线与直线 l 上的动点，以 OC 为一边且顶点为 O，C，P，D 的四边形是平行四边形，求所有符合条件的 P 点坐标 26 已知 D 是 RtABC 斜边 AB 的中点， ACB90， ABC30， 过点 D 作 RtDEF 使DEF90，DFE30，连接 CE 并延长 CE 到 P，使 EPCE，连接 BE，FP， BP，设 BC 与 DE 交于 M，PB 与 EF 交于 N （1）如图 1，当 D，B，F 共线时，求证： EBEP； EFP30； （2）如图 2，当 D，B，F 不共线时，连接 BF，求证：BFD+EFP30 2020 年湖南
10、省常德市中考数学试卷年湖南省常德市中考数学试卷 参考答案与试题解析参考答案与试题解析 一选择题（共一选择题（共 8 小题）小题） 14 的倒数为（ ） A B2 C1 D4 【分析】根据倒数的意义，乘积是 1 的两个数叫做互为倒数，求倒数的方法，是把一个 数的分子和分母互换位置即可，是带分数的化成假分数，再把分子分母互换位置，据此 解答 【解答】解：4 的倒数为 故选：A 2下面几种中式窗户图形既是轴对称又是中心对称的是（ ） A B C D 【分析】根据轴对称图形与中心对称图形的概念求解 【解答】解：A、不是轴对称图形，也不是中心对称图形，故本选项不合题意； B、不是轴对称图形，也不是中心对
11、称图形，故本选项不合题意； C、既是轴对称图形，又是中心对称图形，故此选项正确； D、不是轴对称图形，是中心对称图形，故本选项不合题意； 故选：C 3如图，已知 ABDE，130，235，则BCE 的度数为（ ） A70 B65 C35 D5 【分析】根据平行线的性质和130，235，可以得到BCE 的度数，本题得 以解决 【解答】解：作 CFAB， ABDE， CFDE， ABDEDE， 1BCF，FCE2， 130，235， BCF30，FCE35， BCE65， 故选：B 4下列计算正确的是（ ） Aa2+b2（a+b）2 Ba2+a4a6 Ca10a5a2 Da2a3a5 【分析】根据
12、完全平方公式、合并同类项法则、同底数幂的乘除法计算得到结果，即可 作出判断 【解答】解：A、a2+2ab+b2（a+b）2，原计算错误，故此选项不符合题意； B、a2与 a4不是同类项不能合并，原计算错误，故此选项不符合题意； C、a10a5a5，原计算错误，故此选项不符合题意； D、a2a3a5，原计算正确，故此选项符合题意； 故选：D 5下列说法正确的是（ ） A明天的降水概率为 80%，则明天 80%的时间下雨，20%的时间不下雨 B抛掷一枚质地均匀的硬币两次，必有一次正面朝上 C了解一批花炮的燃放质量，应采用抽样调查方式 D一组数据的众数一定只有一个 【分析】根据必然事件的概念、众数的
13、定义、随机事件的概率逐项分析即可得出答案 【解答】解：A、明天的降水概率为 80%，则明天下雨可能性较大，故本选项错误； B、抛掷一枚质地均匀的硬币两次，正面朝上的概率是，故本选项错误； C、了解一批花炮的燃放质量，应采用抽样调查方式，故本选项正确； D、一组数据的众数不一定只有一个，故本选项错误； 故选：C 6一个圆锥的底面半径 r10，高 h20，则这个圆锥的侧面积是（ ） A100 B200 C100 D200 【分析】先利用勾股定理计算出母线长，然后利用扇形的面积公式计算这个圆锥的侧面 积 【解答】解：这个圆锥的母线长10， 这个圆锥的侧面积21010100 故选：C 7二次函数 ya
14、x2+bx+c（a0）的图象如图所示，下列结论： b24ac0；abc0；4a+b0；4a2b+c0 其中正确结论的个数是（ ） A4 B3 C2 D1 【分析】先由抛物线与 x 周董交点个数判断出结论，利用抛物线的对称轴为 x2，判 断出结论，先由抛物线的开口方向判断出 a0，进而判断出 b0，再用抛物线与 y 轴的交点的位置判断出 c0，判断出结论，最后用 x2 时，抛物线在 x 轴下方， 判断出结论，即可得出结论 【解答】解：由图象知，抛物线与 x 轴有两个交点， 方程 ax2+bx+c0 有两个不相等的实数根， b24ac0，故正确， 由图象知，抛物线的对称轴直线为 x2， 2， 4a
15、+b0，故正确， 由图象知，抛物线开口方向向下， a0， 4a+b0， b0，而抛物线与 y 轴的交点在 y 轴的正半轴上， c0， abc0，故正确， 由图象知，当 x2 时，y0， 4a2b+c0，故错误， 即正确的结论有 3 个， 故选：B 8如图，将一枚跳棋放在七边形 ABCDEFG 的顶点 A 处，按顺时针方向移动这枚跳棋 2020 次移动规则是：第 k 次移动 k 个顶点（如第一次移动 1 个顶点，跳棋停留在 B 处，第 二次移动 2 个顶点，跳棋停留在 D 处） ，按这样的规则，在这 2020 次移动中，跳棋不可 能停留的顶点是（ ） AC、E BE、F CG、C、E DE、C、
16、F 【分析】设顶点 A，B，C，D，E，F，G 分别是第 0，1，2，3，4，5，6 格，因棋子移 动了 k 次后走过的总格数是 1+2+3+kk （k+1） ， 然后根据题目中所给的第 k 次依次 移动 k 个顶点的规则，可得到不等式最后求得解 【解答】解：经实验或按下方法可求得顶点 C，E 和 F 棋子不可能停到 设顶点 A，B，C，D，E，F，G 分别是第 0，1，2，3，4，5，6 格， 因棋子移动了 k 次后走过的总格数是 1+2+3+kk（k+1） ，应停在第k（k+1）7p 格， 这时 P 是整数，且使 0k（k+1）7p6，分别取 k1，2，3，4，5，6，7 时， k（k+1
17、）7p1，3，6，3，1，0，0，发现第 2，4，5 格没有停棋， 若 7k2020， 设 k7+t（t1，2，3）代入可得，k（k+1）7p7m+t（t+1） ， 由此可知，停棋的情形与 kt 时相同， 故第 2，4，5 格没有停棋，即顶点 C，E 和 F 棋子不可能停到 故选：D 二填空题（共二填空题（共 8 小题）小题） 9分解因式：xy24x x（y+2） （y2） 【分析】原式提取 x，再利用平方差公式分解即可 【解答】解：原式x（y24）x（y+2） （y2） ， 故答案为：x（y+2） （y2） 10若代数式在实数范围内有意义，则 x 的取值范围是 x3 【分析】根据二次根式有意
18、义的条件可得 2x60，再解即可 【解答】解：由题意得：2x60， 解得：x3， 故答案为：x3 11计算：+ 3 【分析】直接化简二次根式进而合并得出答案 【解答】解：原式+2 3 故答案为：3 12如图，若反比例函数 y（x0）的图象经过点 A，ABx 轴于 B，且AOB 的面积 为 6，则 k 12 【分析】根据反比例函数比例系数的几何意义即可解决问题 【解答】解：ABOB， SAOB6， k12， 反比例函数的图象在二四象限， k0， k12， 故答案为12 134 月 23 日是世界读书日，这天某校为了解学生课外阅读情况，随机收集了 30 名学生每 周课外阅读的时间，统计如表： 阅读
19、时间（x 小时） x3.5 3.5x5 5x6.5 x6.5 人数 12 8 6 4 若该校共有1200名学生， 试估计全校每周课外阅读时间在5小时以上的学生人数为 400 人 【分析】用总人数每周课外阅读时间在 5 小时以上的学生人数所占的百分比即可得到 结论 【解答】解：1200400（人） ， 答：估计全校每周课外阅读时间在 5 小时以上的学生人数为 400 人 14今年新冠病毒疫情初期，口罩供应短缺，某地规定：每人每次限购 5 只李红出门买口 罩时，无论是否买到，都会消耗家里库存的口罩一只，如果有口罩买，他将买回 5 只已 知李红家原有库存 15 只，出门 10 次购买后，家里现有口罩
20、 35 只请问李红出门没有买 到口罩的次数是 4 次 【分析】设李红出门没有买到口罩的次数是 x，买到口罩的次数是 y，根据买口罩的次数 是 10 次和家里现有口罩 35 只，可列出关于 x 和 y 的二元一次方程组，求解即可 【解答】解：设李红出门没有买到口罩的次数是 x，买到口罩的次数是 y，由题意得： ， 整理得：， 解得： 故答案为：4 15如图 1，已知四边形 ABCD 是正方形，将DAE，DCF 分别沿 DE，DF 向内折叠得 到图 2， 此时 DA 与 DC 重合 （A、 C 都落在 G 点） ， 若 GF4， EG6， 则 DG 的长为 12 【分析】设正方形 ABCD 的边长
21、为 x，由翻折及已知线段的长，可用含 x 的式子分别表示 出 BE、BF 及 EF 的长；在 RtBEF 中，由勾股定理得关于 x 的方程，解得 x 的值，即 为 DG 的长 【解答】解：设正方形 ABCD 的边长为 x，由翻折可得： DGDADCx， GF4，EG6， AEEG6，CFGF4， BEx6，BFx6，EF6+410，如图 1 所示： 在 RtBEF 中，由勾股定理得： BE2+BF2EF2， （x6）2+（x4）2102， x212x+36+x28x+16100， x210x240， （x+2） （x12）0， x12（舍） ，x212 DG12 故答案为：12 16阅读理解：
22、对于 x3（n2+1）x+n 这类特殊的代数式可以按下面的方法分解因式： x3（n2+1）x+nx3n2xx+nx（x2n2）（xn）x（xn） （x+n）（xn） （xn） （x2+nx1） 理解运用：如果 x3（n2+1）x+n0，那么（xn） （x2+nx1）0，即有 xn0 或 x2+nx10， 因此，方程 xn0 和 x2+nx10 的所有解就是方程 x3（n2+1）x+n0 的解 解决问题：求方程 x35x+20 的解为 x2 或 x1+或 x1 【分析】将原方程左边变形为 x34xx+20，再进一步因式分解得（x2）x（x+2） 10，据此得到两个关于 x 的方程求解可得 【解答
23、】解：x35x+20， x34xx+20， x（x24）（x2）0， x（x+2） （x2）（x2）0， 则（x2）x（x+2）10，即（x2） （x2+2x1）0， x20 或 x2+2x10， 解得 x2 或 x1， 故答案为：x2 或 x1+或 x1 三解答题（共三解答题（共 10 小题）小题） 17计算：20+（） 1 4tan45 【分析】先计算 20、 （） 1、tan45，再按运算顺序求值即可 【解答】解：原式1+3241 1+64 3 18解不等式组 【分析】首先分别解出两个不等式的解集，再根据解集的规律确定不等式组的解集 【解答】解：， 由得：x5， 由得：x1， 不等式组的
24、解集为：1x5 19先化简，再选一个合适的数代入求值： （x+1） 【分析】根据分式的减法和除法可以化简题目中的式子，然后选取一个使得原分式有意 义的值代入化简后的式子即可解答本题 【解答】解： （x+1） ， 当 x2 时，原式 20第 5 代移动通信技术简称 5G，某地已开通 5G 业务，经测试 5G 下载速度是 4G 下载速 度的 15 倍，小明和小强分别用 5G 与 4G 下载一部 600 兆的公益片，小明比小强所用的 时间快 140 秒，求该地 4G 与 5G 的下载速度分别是每秒多少兆？ 【分析】首先设该地 4G 的下载速度是每秒 x 兆，则该地 5G 的下载速度是每秒 15x 兆
25、， 根据题意可得等量关系： 4G 下载 600 兆所用时间5G 下载 600 兆所用时间140 秒 然 后根据等量关系，列出分式方程，再解即可 【解答】解：设该地 4G 的下载速度是每秒 x 兆，则该地 5G 的下载速度是每秒 15x 兆， 由题意得：140， 解得：x4， 经检验：x4 是原分式方程的解，且符合题意， 15460， 答：该地 4G 的下载速度是每秒 4 兆，则该地 5G 的下载速度是每秒 60 兆 21已知一次函数 ykx+b（k0）的图象经过 A（3，18）和 B（2，8）两点 （1）求一次函数的解析式； （2）若一次函数 ykx+b（k0）的图象与反比例函数 y（m0）的
26、图象只有一个 交点，求交点坐标 【分析】 （1）直接把（3，18） ， （2，8）代入一次函数 ykx+b 中可得关于 k、b 的方 程组，再解方程组可得 k、b 的值，进而求出一次函数的解析式； （2）联立一次函数解析式和反比例函数解析式，根据题意得到0，解方程即可得到 结论 【解答】解： （1）把（3，18） ， （2，8）代入一次函数 ykx+b（k0） ，得 ， 解得， 一次函数的解析式为 y2x+12； （2）一次函数 ykx+b（k0）的图象与反比例函数 y（m0）的图象只有一个 交点， 只有一组解， 即 2x2+12xm0 有两个相等的实数根， 12242（m）0， m18 把
27、m18 代入求得该方程的解为：x3， 把 x3 代入 y2x+12 得：y6， 即所求的交点坐标为（3，6） 22如图 1 是自动卸货汽车卸货时的状态图，图 2 是其示意图汽车的车厢采用液压机构、 车厢的支撑顶杆 BC 的底部支撑点 B 在水平线 AD 的下方，AB 与水平线 AD 之间的夹角 是 5，卸货时，车厢与水平线 AD 成 60，此时 AB 与支撑顶杆 BC 的夹角为 45，若 AC 2米 ， 求BC的 长度 （ 结果 保 留一 位 小数 ） （参考数据：sin650.91，cos650.42，tan652.14，sin700.94，cos70 0.34，tan702.75，1.41
28、） 【分析】直接过点 C 作 CFAB 于点 F，利用锐角三角函数关系得出 CF 的长，进而得 出 BC 的长 【解答】方法一：解：如图 1，过点 C 作 CFAB 于点 F， 在 RtACF 中， sinCABsin（60+5）sin65， CFACsin6520.911.82， 在 RtBCF 中， ABC45， CFBF， BCCF1.411.822.56622.6， 答：所求 BC 的长度约为 2.6 米 方法二：解：如图 2，过点 A 作 AEBC 于点 E， 在 RtACE 中，C180654570， cosCcos70， 即 CEACcos7020.340.68， sinCsin
29、70， 即 AEACsin7020.941.88， 又在 RtAEB 中，ABC45， AEBE， BCBE+CE0.68+1.882.562.6， 答：所求 BC 的长度约为 2.6 米 23今年 24 月某市出现了 200 名新冠肺炎患者，市委根据党中央的决定，对患者进行了 免费治疗图 1 是该市轻症、重症、危重症三类患者的人数分布统计图（不完整） ，图 2 是这三类患者的人均治疗费用统计图请回答下列问题 （1）轻症患者的人数是多少？ （2）该市为治疗危重症患者共花费多少万元？ （3）所有患者的平均治疗费用是多少万元？ （4）由于部分轻症患者康复出院，为减少病房拥挤，拟对某病房中的 A、B
30、、C、D、E 五位患者任选两位转入另一病房，请用树状图法或列表法求出恰好选中 B、D 两位患者 的概率 【分析】 （1）因为总人数已知，由轻症患者所占的百分比即可求出其的人数； （2）求出该市危重症患者所占的百分比，即可求出其共花费的钱数； （3）用加权平均数公式求出各种患者的平均费用即可； （4）首先根据题意列出表格，然后由表格求得所有等可能的结果与恰好选中 B、D 两位 同学的情况，再利用概率公式即可求得答案 【解答】解： （1）轻症患者的人数20080%160（人） ； （2）该市为治疗危重症患者共花费钱数200（180%15%）10100（万元） ； （3）所有患者的平均治疗费用2.1
31、5（万元） ； （4）列表得： A B C D E A （B，A） （C，A） （D，A） （E，A） B （A，B） （C，B） （D，B） （E，B） C （A，C） （B，C） （D，C） （E，C） D （A，D） （B，D） （C，D） （E，D） E （A，E） （B，E） （C，E） （D，E） 由列表格，可知：共有 20 种等可能的结果，恰好选中 B、D 两位同学的有 2 种情况， P（恰好选中 B、D） 24如图，已知 AB 是O 的直径，C 是O 上的一点，D 是 AB 上的一点，DEAB 于 D， DE 交 BC 于 F，且 EFEC （1）求证：EC 是O 的切线； （
32、2）若 BD4，BC8，圆的半径 OB5，求切线 EC 的长 【分析】 （1）连接 OC，由等腰三角形的性质和直角三角形的性质可得OCB+ECF 90，可证 EC 是O 的切线； （2） 由勾股定理可求 AC6， 由锐角三角函数可求 BF5， 可求 CF3， 通过证明OAC ECF，可得，可求解 【解答】解： （1）连接 OC， OCOB， OBCOCB， DEAB， OBC+DFB90， EFEC， ECFEFCDFB， OCB+ECF90， OCCE， EC 是O 的切线； （2）AB 是O 的直径， ACB90， OB5， AB10， AC6， cosABC， ， BF5， CFBCBF
33、3， ABC+A90，ABC+BFD90， BFDA， ABFDECFEFC， OAOC， OCAABFDECFEFC， OACECF， ， EC 25如图，已知抛物线 yax2过点 A（3，） （1）求抛物线的解析式； （2）已知直线 l 过点 A，M（，0）且与抛物线交于另一点 B，与 y 轴交于点 C，求证： MC2MAMB； （3）若点 P，D 分别是抛物线与直线 l 上的动点，以 OC 为一边且顶点为 O，C，P，D 的四边形是平行四边形，求所有符合条件的 P 点坐标 【分析】 （1）利用待定系数法即可解决问题 （2）构建方程组确定点 B 的坐标，再利用平行线分线段成比例定理解决问题
34、即可 （3）如图 2 中，设 P（t，t2） ，根据 PDCD 构建方程求出 t 即可解决问题 【解答】解： （1）把点 A（3，）代入 yax2， 得到9a， a， 抛物线的解析式为 yx2 （2）设直线 l 的解析式为 ykx+b，则有， 解得， 直线 l 的解析式为 yx+， 令 x0，得到 y， C（0，） ， 由，解得或， B（1，） ， 如图 1 中，过点 A 作 AA1x 轴于 A1，过 B 作 BB1x 轴于 B1，则 BB1OCAA1， ， ， 即 MC2MAMB （3）如图 2 中，设 P（t，t2） OC 为一边且顶点为 O，C，P，D 的四边形是平行四边形， PDOC，
35、PDOC， D（t，t+） ， |t2（t+）|， 整理得：t2+2t60 或 t2+2t0， 解得 t1或1或2 或 0（舍弃） ， P（1，2+）或（1+，2）或（2，1） 26 已知 D 是 RtABC 斜边 AB 的中点， ACB90， ABC30， 过点 D 作 RtDEF 使DEF90，DFE30，连接 CE 并延长 CE 到 P，使 EPCE，连接 BE，FP， BP，设 BC 与 DE 交于 M，PB 与 EF 交于 N （1）如图 1，当 D，B，F 共线时，求证： EBEP； EFP30； （2）如图 2，当 D，B，F 不共线时，连接 BF，求证：BFD+EFP30 【分
36、析】 （1）证明CBP 是直角三角形，根据直角三角形斜边中线可得结论； 根据同位角相等可得 BCEF，由平行线的性质得 BPEF，可得 EF 是线段 BP 的垂 直平分线，根据等腰三角形三线合一的性质可得PFEBFE30； （2） 如图 2， 延长 DE 到 Q， 使 EQDE， 连接 CD， PQ， FQ， 证明QEPDEC （SAS） ， 则 PQDCDB，由 QEDE，DEF90，知 EF 是 DQ 的垂直平分线，证明FQP FDB（SAS） ，再由 EF 是 DQ 的垂直平分线，可得结论 【解答】证明（1）ACB90，ABC30， A903060， 同理EDF60， AEDF60， A
37、CDE， DMBACB90， D 是 RtABC 斜边 AB 的中点，ACDM， ， 即 M 是 BC 的中点， EPCE，即 E 是 PC 的中点， EDBP， CBPDMB90， CBP 是直角三角形， BEPCEP； ABCDFE30， BCEF， 由知：CBP90， BPEF， EBEP， EF 是线段 BP 的垂直平分线， PFBF， PFEBFE30； （2）如图 2，延长 DE 到 Q，使 EQDE，连接 CD，PQ，FQ， ECEP，DECQEP， QEPDEC（SAS） ， 则 PQDCDB， QEDE，DEF90 EF 是 DQ 的垂直平分线， QFDF， CDAD， CDAA60， CDB120， FDB120FDC120（60+EDC）60EDC60EQP FQP， FQPFDB（SAS） ， QFPBFD， EF 是 DQ 的垂直平分线， QFEEFD30， QFP+EFP30， BFD+EFP30
