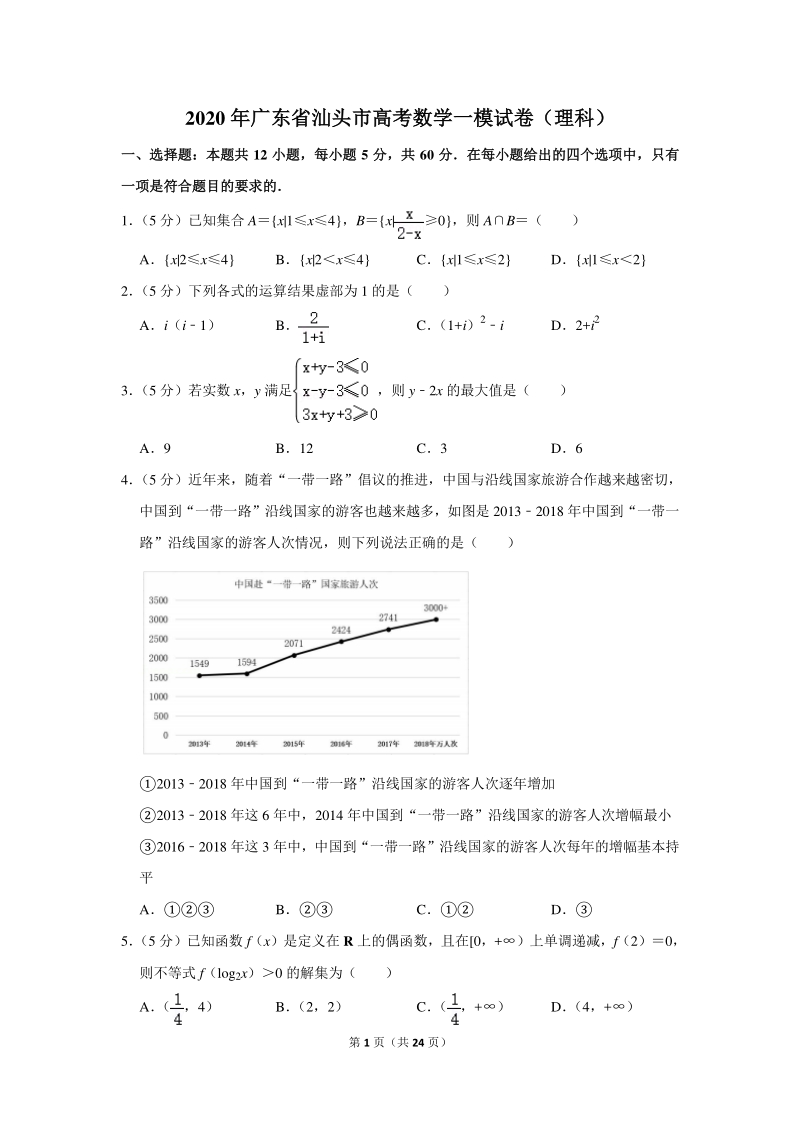
1、已知集合 Ax|1x4，Bx|0，则 AB（ ） Ax|2x4 Bx|2x4 Cx|1x2 Dx|1x2 2 （5 分）下列各式的运算结果虚部为 1 的是（ ） Ai（i1） B C （1+i）2i D2+i2 3 （5 分）若实数 x，y 满足，则 y2x 的最大值是（ ） A9 B12 C3 D6 4 （5 分）近年来，随着“一带一路”倡议的推进，中国与沿线国家旅游合作越来越密切， 中国到“一带一路”沿线国家的游客也越来越多，如图是 20132018 年中国到“一带一 路”沿线国家的游客人次情况，则下列说法正确的是（ ） 20132018 年中国到“一带一路”沿线国家的游客人次逐年增加 2
2、0132018 年这 6 年中，2014 年中国到“一带一路”沿线国家的游客人次增幅最小 20162018 年这 3 年中，中国到“一带一路”沿线国家的游客人次每年的增幅基本持 平 A B C D 5 （5 分）已知函数 f（x）是定义在 R 上的偶函数，且在0，+）上单调递减，f（2）0， 则不等式 f（log2x）0 的解集为（ ） A （，4） B （2，2） C （，+） D （4，+） 第 2 页（共 24 页） 6 （5 分）已知函数 f（x）Asin（x+） （A0，0，|）的图象与直线 ya（0 aA）的三个相邻交点的横坐标分别为 2、4、8，则 f（x）的单调递减区间为（ ）
3、 A6k，6k+3，kZ B6k3，6k，kZ C6k，6k+3，kZ D6k3，6k，kZ 7 （5 分） “今有城，下广四丈，上广二丈，高五丈，袤一百二十六丈五尺 ”这是我国古代 数学名著九章算术卷第五中“商功”中的问题意思为“现有城（如图，等腰梯形 的直棱柱体） ，下底长 4 丈，上底长 2 丈，高 5 丈，纵长 126 丈 5 尺（1 丈10 尺） ” ，则 该问题中“城”的体积等于（ ） A1.8975106立方尺 B3.7950106立方尺 C2.5300105立方尺 D1.8975105立方尺 8 （5 分）已知四边形 ABCD 为平行四边形，|，|，M 为 CD 中点， 2，则
4、（ ） A B C1 D 9 （5 分）ABC 中，角 A，B，C 所对应的分别为 a，b，c，且（a+b） （sinAsinB）（c b）sinC，若 a2，则ABC 的面积的最大值是（ ） A1 B C2 D2 10 （5 分）在（x2x2）5的展开式中，x3的系数为（ ） A40 B160 C120 D200 11 （5 分）体积为的三棱锥 ABCD 中，BCACBDAD3，CD2，AB 2，则该三棱锥外接球的表面积为（ ） A20 B C D 12 （5 分）若函数 f（x）在其图象上存在不同的两点 A（x1，y1） ，B（x2，y2） ，其坐标满足 条件： |x1x2+y1y2|的最
5、大值为 0， 则称 f （x） 为 “柯西函数” ， 第 3 页（共 24 页） 则下列函数： f（x）x+（x0） ； f（x）lnx（0x3） ； f（x）cosx； f（x）x21 其中为“柯西函数”的个数为（ ） A1 B2 C3 D4 二、填空题：本题共二、填空题：本题共 4 小题，每小题小题，每小题 5 分，共分，共 20 分分. 13 （5 分）曲线 f（x）x2e x 在点（1，f（1） ）处的切线方程为 14 （5 分）若双曲线 C：1（a0，b0）的两个顶点将焦距三等分，则双曲线 C 的渐近线方程为 15 （5 分） “新冠肺炎”爆发后，某医院由甲、乙、丙、丁、戊 5 位医
6、生组成的专家组到某 市参加抗击疫情五位医生去乘高铁，按规定每位乘客在进站前都需要安检，当时只有 3 个安检口开通，且没有其他旅客进行安检.5 位医生分别从 3 个安检口进行安检，每个安 检口都有医生去安检且不同的安检顺序视为不同的安检，则甲、乙 2 位医生不在同一个 安检口进行安检的概率为 16 （5 分）直线 l：xty+10（t0）和抛物线 C：y24x 相交于不同两点 A、B，设 AB 的中点为 M，抛物线 C 的焦点为 F，以 MF 为直径的圆与直线 l 相交另一点为 N，且满足 |MN|NF|，则直线 l 的方程为 三、解答题：共三、解答题：共 70 分，解答应写出文字说明、证明过程
7、或演算步骤第分，解答应写出文字说明、证明过程或演算步骤第 17-21 题为必考题，题为必考题， 每个试题考生都必须作答第每个试题考生都必须作答第 22、23 题为选考题，考生根据要求作答 （一）必考题：共题为选考题，考生根据要求作答 （一）必考题：共 60 分分. 17 （12 分）已知 Sn为数列an的前 n 项和，且 Sn+22an，nN* （1）求数列an的通项公式； （2）令 bn，设数列bn的前项和为 Tn，若 Tn，求 n 的最 小值 18 （12 分）在四棱锥 PABCD 中，平面 PAC平面 ABCD，且有 ABDC，ACCD 第 4 页（共 24 页） DAAB （1）证明：
8、BCPA； （2）若 PAPCAC，求平面 PAD 与平面 PBC 所成的锐二面角的余弦值 19 （12 分）为评估设备 M 生产某种零件的性能，从设备 M 生产零件的流水线上随机抽取 100 件零件作为样本，测量其直径后，整理得到如表： 直径 /mm 58 59 61 62 63 64 65 66 67 68 69 70 71 73 合计 件数 1 1 3 5 6 19 33 18 4 4 2 1 2 1 100 经计算，样本零件直径的平均值 65，标准差2.2，以频率值作为概率的估计值 （1）为评判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为 x，并 根据以下不等式进行评判
9、（P 表示相应时间的概率） ：P（X+）0.6826， P（2X+2）0.9544，P（3X+3）0.9974评判规则为： 若同时满足上述三个不等式，则设备等级为甲；仅满足其中两个，则等级为乙，若仅满 足其中一个，则等级为丙；若全部不满足，则等级为丁试判断设备 M 的性能等级 （2）将直径小于 2或直径大于 +2的零件认为是次品 从设备 M 的生产流水线上任意抽取 2 件零件，求其中次品个数的数学期望 E（Y） ； 从样本中任意抽取 2 件零件，求其中次品个数的数学期望 E（Z） 20 （12 分）已知椭圆 C 的中心在坐标原点 O，其右焦点为 F（1，0） ，以坐标原点 O 为圆 心，椭圆短
10、半轴长为半径的圆与直线 xy+0 的相切 （1）求椭圆 C 的方程； （2）经过点 F 的直线 l1，l2分别交椭圆 C 于 A、B 及 C、D 四点，且 l1l2，探究：是否 存在常数 ，使|AB|+|CD|AB|CD|恒成立 21 （12 分）已知函数 f（x）x2+ax+lnx（aR） 第 5 页（共 24 页） （1）讨论函数 f（x）的单调性； （2）若 f（x）存在两个极值点 x1，x2且|x1x2|，求|f（x1）f（x2）|的最大值 （二）选考题：共（二）选考题：共 10 分请考生在第分请考生在第 22、23 题中任选一题作答如果多做，则按所做的题中任选一题作答如果多做，则按所
11、做的 第一题记分第一题记分选修选修 4-4：坐标系与参数方程：坐标系与参数方程 22 （10 分）在平面直角坐标系 xOy 中，曲线 C 的参数方程为：（ 为参数） ， 已知直线 l1：xy0，直线 l2：xy0 以坐标原点为极点，x 轴正半轴为极轴， 建立极坐标系 （1）求曲线 C 以及直线 l1，l2的极坐标方程； （2）若直线 l1与曲线 C 分别交于 O、A 两点，直线 l2与曲线 C 分别交于 O、B 两点，求 AOB 的面积 选修选修 4-5：不等式选讲：不等式选讲（10 分）分） 23设函数 f（x）|x+a| （1）当 a2 时，求不等式f（x）的解集； （2）若 0，f（1）
12、，f（ba2），证明|2a+b4| 第 6 页（共 24 页） 2020 年广东省汕头市高考数学一模试卷（理科）年广东省汕头市高考数学一模试卷（理科） 参考答案与试题解析参考答案与试题解析 一、选择题：本题共一、选择题：本题共 12 小题，每小题小题，每小题 5 分，共分，共 60 分在每小题给出的四个选项中，只有分在每小题给出的四个选项中，只有 一项是符合题目的要求的一项是符合题目的要求的 1 （5 分）已知集合 Ax|1x4，Bx|0，则 AB（ ） Ax|2x4 Bx|2x4 Cx|1x2 Dx|1x2 【分析】求出集合 A，B，由此能求出 AB 【解答】解：集合 Ax|1x4， Bx|
13、0x|0x2， ABx|1x2 故选：D 【点评】本题考查交集的求法，考查交集定义等基础知识，考查运算求解能力，是基础 题 2 （5 分）下列各式的运算结果虚部为 1 的是（ ） Ai（i1） B C （1+i）2i D2+i2 【分析】分别利用复数代数形式的乘除运算化简四个选项得答案 【解答】解：i（i1）1i， ， （1+i）2ii， 2+i21 运算结果虚部为 1 的是（1+i）2i 故选：C 【点评】本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题 3 （5 分）若实数 x，y 满足，则 y2x 的最大值是（ ） A9 B12 C3 D6 第 7 页（共 24 页） 【分析
14、】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优 解，求得最优解的坐标，代入目标函数得答案 【解答】解：由实数 x，y 满足，作出可行域如图， 令 zy2x，化为 y2x+z， 联立，解得 A（3，6） 由图可知，当直线过 A 时，y2x 有最大值为 12 故选：B 【点评】本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题 4 （5 分）近年来，随着“一带一路”倡议的推进，中国与沿线国家旅游合作越来越密切， 中国到“一带一路”沿线国家的游客也越来越多，如图是 20132018 年中国到“一带一 路”沿线国家的游客人次情况，则下列说法正确的是（ ） 2013
15、2018 年中国到“一带一路”沿线国家的游客人次逐年增加 20132018 年这 6 年中，2014 年中国到“一带一路”沿线国家的游客人次增幅最小 第 8 页（共 24 页） 20162018 年这 3 年中，中国到“一带一路”沿线国家的游客人次每年的增幅基本持 平 A B C D 【分析】利用折线图的性质直接求解 【解答】解：由 20132018 年中国到“一带一路”沿线国家的游客人次情况和折线图， 得： 在中，20132018 年中国到“一带一路”沿线国家的游客人次逐年增加，故正确； 在中，20132018 年这 6 年中，2014 年中国到“一带一路”沿线国家的游客人次增幅 最小，故正
16、确； 在中，20162018 年这 3 年中，中国到“一带一路”沿线国家的游客人次每年的增幅 基本持平，故正确 故选：A 【点评】本题考查命题真假的判断，考查折线图的性质等基础知识，考查运算求解能力， 是基础题 5 （5 分）已知函数 f（x）是定义在 R 上的偶函数，且在0，+）上单调递减，f（2）0， 则不等式 f（log2x）0 的解集为（ ） A （，4） B （2，2） C （，+） D （4，+） 【分析】根据题意，由函数 f（x）的奇偶性与 f（2）0 可得 f（log2x）0f（|log2x|） f（2） ，结合函数 f（x）的单调性分析可原不等式等价于|log2x|2，解可得
17、 x 的取值范 围，即可得答案 【解答】解：根据题意，函数 f（x）是定义在 R 上的偶函数，且 f（2）0， 则 f（log2x）0f（|log2x|）f（2） ， 又由 f（x）在0，+）上单调递减，f（|log2x|）f（2）|log2x|2， 变形可得：2log2x2， 解可得：x4，不等式的解集为（，4） ； 故选：A 【点评】本题考查函数的奇偶性与单调性的综合应用，注意将原不等式转化为关于 x 的 不等式，属于基础题 第 9 页（共 24 页） 6 （5 分）已知函数 f（x）Asin（x+） （A0，0，|）的图象与直线 ya（0 aA）的三个相邻交点的横坐标分别为 2、4、8，
18、则 f（x）的单调递减区间为（ ） A6k，6k+3，kZ B6k3，6k，kZ C6k，6k+3，kZ D6k3，6k，kZ 【分析】由题意利用正弦函数的图象和性质，求出 f（x）的单调递减区间 【解答】解：函数 f（x）Asin（x+） （A0，0，|）的图象与直线 y a（0aA）的三个相邻交点的横坐标分别为 2、4、8， 3，6，633， T6，故函数的减区间为6k+3，6k+6，即6k3，6k，kZ， 故选：D 【点评】本题主要考查正弦函数的图象和性质，属于中档题 7 （5 分） “今有城，下广四丈，上广二丈，高五丈，袤一百二十六丈五尺 ”这是我国古代 数学名著九章算术卷第五中“商功
19、”中的问题意思为“现有城（如图，等腰梯形 的直棱柱体） ，下底长 4 丈，上底长 2 丈，高 5 丈，纵长 126 丈 5 尺（1 丈10 尺） ” ，则 该问题中“城”的体积等于（ ） A1.8975106立方尺 B3.7950106立方尺 C2.5300105立方尺 D1.8975105立方尺 【分析】由已知求出直四棱柱的底面积，再由棱柱的体积公式求解 【解答】解：由题意，直四棱柱的底面积 S平方尺； 又直四棱柱的高为 1265 尺， 该问题中“城”的体积等于 150012651.8975106立方尺 故选：A 【点评】本题考查直四棱柱体积的求法，是基础的计算题 8 （5 分）已知四边形
20、ABCD 为平行四边形，|，|，M 为 CD 中点， 第 10 页（共 24 页） 2，则（ ） A B C1 D 【分析】先根据已知条件可求得，而 ，然后将其展开，利用平面向量数量积进行运算求解即可 【解答】解：|，|，M 为 CD 中点，2， ， ， 故选：A 【点评】本题考查平面向量的混合运算，尤其是平面向量的数量积，考查学生的转化能 力和计算能力，属于基础题 9 （5 分）ABC 中，角 A，B，C 所对应的分别为 a，b，c，且（a+b） （sinAsinB）（c b）sinC，若 a2，则ABC 的面积的最大值是（ ） A1 B C2 D2 【分析】由已知利用正弦定理可得 a2b2
21、+c2bc，由余弦定理可得 cosA，结合范围 A（0，） ，可求 A 的值；再利用余弦定理，基本不等式可求 bc4，当且仅当 bc2 时，取等号，利用三角形的面积公式即可求解 【解答】解：由（a+b） （sinAsinB）（cb）sinC， 利用正弦定理可得： （a+b） （ab）（cb）c， 即 a2b2+c2bc， 所以由余弦定理可得：cosA， 而 A（0，） ， 所以 A； 因为 a2， 所以可得：4b2+c2bc2bcbcbc， 即 bc4，当且仅当 bc2 时，取等号， 第 11 页（共 24 页） 所以 SABCbcsinA4，即ABC 面积的最大值为 故选：B 【点评】本题主
22、要考查了正弦定理，余弦定理，基本不等式，三角形的面积公式在解三 角形中的综合应用，考查了计算能力和转化思想，属于基础题 10 （5 分）在（x2x2）5的展开式中，x3的系数为（ ） A40 B160 C120 D200 【分析】先把（x2x2）5变形为（x+1）5（x2）5，再利用二项式定理中的通项公式 求出结果 【解答】解：（x2x2）5（x+1）5（x2）5，x3的系数为 C C （2）5+C C （2）4+C C （2）3+C C （2）2120 故选：C 【点评】本题主要考查二项式定理的应用，属于基础题 11 （5 分）体积为的三棱锥 ABCD 中，BCACBDAD3，CD2，AB
23、2，则该三棱锥外接球的表面积为（ ） A20 B C D 【分析】由题意取 AB 的中点 E，连接 DE，CE，因为 BCACBDAD3，所以 CE AB，DEAB，DECEE， 所以 AB面 CDE，且 DECE，取 CD 的中点，连接 EP，则 EPCD，再由体积可得 AB 的值，进而求出底面外接圆的半径，及 D 到底面的高，由题意求出外接球的半径，进 而求出外接球的表面积 【解答】解：取 AB 的中点 E，连接 DE，CE，因为 BCACBDAD3，所以 CE AB，DEAB，DECEE， 所以 AB面 CDE，且 DECE，取 CD 的中点，连接 EP，则 EPCD， 所以 VABCD
24、ABSCDEABAB ABAB， 因为 VABCD， 第 12 页（共 24 页） 所以AB，因为 AB2， 所以解得 AB2；AE1，DECE2， 所以 sinACE，所以 sinACB2sinACEcosACE2， 由题意可得 D 在底面的投影在中线 CE 所在的直线上，设为 F，设 DFh， 设底面 ABC 的外接圆的半径为 r， 设圆心为 O， 2r， 所以 r， OECEr2， VABCDSABChAC2sinACBhh，解得 h， 所以 EF， 所以 OFEF+OE+， 过 O作 OO面 ABC 的垂线，作 OHDF 于 H，则四边形 HFOO 为矩形， 设外接球的半径为 R，取
25、OAOBODR， 在三角形 OHD 中，OD2OH2+（DFFH） 2，即 R2OF2+（ OO） 2（ ） 2+（ OO）2， 在三角形 OO中，OC2CO2+OO2r2+OO2即 R2（）2+OO2， 由可得 R2， 所以外接球的表面积 S4R24， 故选：B 【点评】本题考查三棱锥与外接球的半径之间的关系，及球的表面积公式，属于中档题 12 （5 分）若函数 f（x）在其图象上存在不同的两点 A（x1，y1） ，B（x2，y2） ，其坐标满足 条件： |x1x2+y1y2|的最大值为 0， 则称 f （x） 为 “柯西函数” ， 第 13 页（共 24 页） 则下列函数： f（x）x+（
26、x0） ； f（x）lnx（0x3） ； f（x）cosx； f（x）x21 其中为“柯西函数”的个数为（ ） A1 B2 C3 D4 【分析】由“柯西函数”得函数 f（x）在其图象上存在不同的两点 A（x1，y1） ，B（x2， y2由） ，使得、共线，即存在点 A、B 与点 O 共线，分别判断即可 【解答】解：对由柯西不等式得：对任意实数 x1，y1，x2，y2：|x1x2+y1y2| 0 恒成立（当且仅当存在实数 k，使得 x1kx2，y1ky2取 等号） ， 若函数 f （x） 在其图象上存在不同的两点 A （x1， y1） ， B （x2， y2） ， 其坐标满足条件： |x1x2+
27、y1y2| 的最大值为 0， 则函数 f（x）在其图象上存在不同的两点 A（x1，y1） ，B（x2，y2） ， 使得、共线，即存在点 A、B 与点 O 共线 设 AB 的方程为 ykx，由于 ykx（x0）与 f（x）x+只有一个交点，故不是柯 西函数， 对于，由于 y与 f（x）lnx（0x3）有两个交点，故是柯西函数； 对于，取 A（0，0） ，点 B 任意，均满足定义，故是柯西函数 对于取 A（1，0） ，B（1，0） ，均满足定义，故是柯西函数 故选：C 【点评】本题考查了新定义，关键是弄清新定义的含义，属于中档题 二、填空题：本题共二、填空题：本题共 4 小题，每小题小题，每小题
28、5 分，共分，共 20 分分. 13 （5 分）曲线 f（x）x2e x 在点（1，f（1） ）处的切线方程为 xey0 【分析】先求出函数的导数，然后再求出切点处函数值、导数值，最后代入点斜式得切 线方程 第 14 页（共 24 页） 【解答】解：f（x）2xe xx2ex， 故切线为：，即 xey0 故答案为：xey0 【点评】本题考查导数的几何意义和切线方程的求法属于基础题 14 （5 分）若双曲线 C：1（a0，b0）的两个顶点将焦距三等分，则双曲线 C 的渐近线方程为 y 【分析】由题意可得 2a，即 3ac，再由 a，b，c 之间的关系求出 a，b 的关系， 进而求出渐近线 yx，
29、即求出渐近线的方程 【解答】解：双曲线 C：1（a0，b0）的两个顶点将焦距三等分可得：2a ，即 3ac， 所以 9a2c2a2+b2，即 8a2b2， 所以渐近线的方程为：yxx， 故答案为：y 【点评】本题考查双曲线的性质，属于基础题 15 （5 分） “新冠肺炎”爆发后，某医院由甲、乙、丙、丁、戊 5 位医生组成的专家组到某 市参加抗击疫情五位医生去乘高铁，按规定每位乘客在进站前都需要安检，当时只有 3 个安检口开通，且没有其他旅客进行安检.5 位医生分别从 3 个安检口进行安检，每个安 检口都有医生去安检且不同的安检顺序视为不同的安检，则甲、乙 2 位医生不在同一个 安检口进行安检的
30、概率为 【分析】基本事件总数 n+720，甲、 乙 2 位医生在同一个安检口进行安检包含的基本事件个数 m+ 180，由此能求出甲、乙 2 位医生不在同一个安检口进行安检的概率 【解答】解：某医院由甲、乙、丙、丁、戊 5 位医生组成的专家组到某市参加抗击疫情 五位医生去乘高铁，按规定每位乘客在进站前都需要安检， 第 15 页（共 24 页） 当时只有 3 个安检口开通，且没有其他旅客进行安检.5 位医生分别从 3 个安检口进行安 检， 每个安检口都有医生去安检且不同的安检顺序视为不同的安检， 基本事件总数 n+720， 甲、 乙 2 位医生在同一个安检口进行安检包含的基本事件个数 m+ 180
31、， 则甲、乙 2 位医生不在同一个安检口进行安检的概率为 P11 故答案为： 【点评】本题考查概率的求法，考查古典概型、对立事件概率计算公式等基础知识，考 查运算求解能力，是基础题 16 （5 分）直线 l：xty+10（t0）和抛物线 C：y24x 相交于不同两点 A、B，设 AB 的中点为 M，抛物线 C 的焦点为 F，以 MF 为直径的圆与直线 l 相交另一点为 N，且满足 |MN|NF|，则直线 l 的方程为 xy+10 【分析】求得抛物线的焦点 F，联立直线 l 和抛物线的方程，运用韦达定理和中点坐标公 式可得 M 的坐标，设 N（ty01，y0） ，由 NFl，结合两直线垂直的条件
32、，可得 t，y0的 关系式，再由两点的距离公式，化简整理可得 t，可得所求直线方程 【解答】解：y24x 的焦点为 F（1，0） ，联立 xty+10 与 y24x，可得 y24ty+40， 设 A（x1，y1） ，B（x2，y2） ， 可得 y1+y24t，则中点 M（2t21，2t） ， 设 N（ty01，y0） ，由 NFl，可得t，即有 y0， 由|MN|NF|可得|MN|227NF|2， 即为（2t2ty0）2+（2ty0）227（ty02）2+y02， 注意结合 t2y02ty0， 化为 t4t22714ty02714t，即为 t627，解得 t， 可得直线 l 的方程为 xy+1
33、0 故答案为：xy+10 第 16 页（共 24 页） 【点评】本题考查直线和抛物线的综合，考查直线方程和抛物线方程联立，运用韦达定 理和中点坐标公式，考查两点的距离公式，以及圆的性质，以及化简运算求解能力，属 于中档题 三、解答题：共三、解答题：共 70 分，解答应写出文字说明、证明过程或演算步骤第分，解答应写出文字说明、证明过程或演算步骤第 17-21 题为必考题，题为必考题， 每个试题考生都必须作答第每个试题考生都必须作答第 22、23 题为选考题，考生根据要求作答 （一）必考题：共题为选考题，考生根据要求作答 （一）必考题：共 60 分分. 17 （12 分）已知 Sn为数列an的前
34、n 项和，且 Sn+22an，nN* （1）求数列an的通项公式； （2）令 bn，设数列bn的前项和为 Tn，若 Tn，求 n 的最 小值 【分析】 （1）由数列an的前 n 项和与项满足 Sn+22an，nN*消掉和 Sn可得数列an 是等比数列，进而求数列an的通项公式 （2） 由 （1） 得数列bn的通项公式， 列项求和算出 Tn1， 再由若 Tn， 解整数不等式可求 n 的最小值 【解答】解： （1）当 n1 时，S1+22a1，解得 a12， 当 n2 时，Sn1+22an1，Sn+2（Sn1+2）2an2an1，即 an2an1 2，则an是以 2 为首项，2 为公比的等比数列
35、故 an2n （2） ：由（1）可得 bn Tnb1+b2+bn（1）+（）+（）1 ， 又 Tn，即 1， 2n+12021，由于 nN，n10， 故 n 的最小值为 10 【点评】本题考查数列项与和的转化，等比数列的通项公式， “裂项求和” ，解整数不等 第 17 页（共 24 页） 式，考查了推理能力与计算能力，属于中档题 18 （12 分）在四棱锥 PABCD 中，平面 PAC平面 ABCD，且有 ABDC，ACCD DAAB （1）证明：BCPA； （2）若 PAPCAC，求平面 PAD 与平面 PBC 所成的锐二面角的余弦值 【分析】 （1）设 AB2a，则 ACCDDAa，推导出
36、，由余弦定理得 BC ，由勾股定理得 BCAC，从而 BC平面 PAC，由此能证明 BCPA （2） 设 AC2， 取 AC 中点 O， 连结 PO， 则 POAC， PO， 推导出 PO平面 ABCD， 以 C 为原点，CA 为 x 轴，CB 为 y 轴，过 C 作平面 ABCD 的垂线为 z 轴，建立空间直角 坐标系，利用向量法能求出平面 PAD 与平面 PBC 所成的锐二面角的余弦值 【解答】解： （1）证明：设 AB2a，则 ACCDDAa， ACD 是等边三角形， ABDC， 由余弦定理得： 3a2，BC， BC2+AC2AB2，BCAC， 平面 PAC平面 ABCDAC，BC平面
37、ABCD， BC平面 PAC， PA平面 PAC，BCPA （2）解：设 AC2，取 AC 中点 O，连结 PO，则 POAC，PO， 平面 PAC平面 ABCD，PO平面 ABCD， 以 C 为原点，CA 为 x 轴，CB 为 y 轴，过 C 作平面 ABCD 的垂线为 z 轴，建立空间直角 第 18 页（共 24 页） 坐标系， 则 C（0，0，0） ，B（0，2，0） ，P（1，0，） ，A（2，0，0） ，D（1，0） ， （1，0，） ，（1，0） ，（1，0，） ，（0，2，0） ， 设平面 PAD 的法向量 （x，y，z） ， 则，取 z1，得 （） ， 设平面 PBC 的法向量
38、 （a，b，c） ， 则，取 a，得 （） ， 设平面 PAD 与平面 PBC 所成的锐二面角为 则 cos 平面 PAD 与平面 PBC 所成的锐二面角的余弦值为 【点评】本题考查线线垂直的证明，考查二面角的余弦值的求法，考查空间中线线、线 面、面面间的位置关系等基础知识，考查运算求解能力，是中档题 19 （12 分）为评估设备 M 生产某种零件的性能，从设备 M 生产零件的流水线上随机抽取 100 件零件作为样本，测量其直径后，整理得到如表： 直径 /mm 58 59 61 62 63 64 65 66 67 68 69 70 71 73 合计 第 19 页（共 24 页） 件数 1 1
39、3 5 6 19 33 18 4 4 2 1 2 1 100 经计算，样本零件直径的平均值 65，标准差2.2，以频率值作为概率的估计值 （1）为评判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为 x，并 根据以下不等式进行评判（P 表示相应时间的概率） ：P（X+）0.6826， P（2X+2）0.9544，P（3X+3）0.9974评判规则为： 若同时满足上述三个不等式，则设备等级为甲；仅满足其中两个，则等级为乙，若仅满 足其中一个，则等级为丙；若全部不满足，则等级为丁试判断设备 M 的性能等级 （2）将直径小于 2或直径大于 +2的零件认为是次品 从设备 M 的生产流水线上
40、任意抽取 2 件零件，求其中次品个数的数学期望 E（Y） ； 从样本中任意抽取 2 件零件，求其中次品个数的数学期望 E（Z） 【分析】 （）利用条件，可得设备 M 的数据仅满足一个不等式，即可得出结论； （）易知样本中次品共 6 件，可估计设备 M 生产零件的次品率为 0.06 （）由题意可知 YB（2，） ，于是 E（Y）2； （）确定 Z 的取值，求出相应的概率，即可求出其中次品个数 Z 的数学期望 E（Z） 【解答】解： （）P（X+）P（62.8X67.2）0.80.6826，P（ 2X+2） P （60.6X69.4） 0.940.9544， P （3X+3） P （58.4 X7
41、1.6）0.980.9974， 因为设备 M 的数据仅满足一个不等式，故其性能等级为丙；（4 分） （）易知样本中次品共 6 件，可估计设备 M 生产零件的次品率为 0.06 （）由题意可知 YB（2，） ，于是 E（Y）2；（8 分） （）由题意可知 Z 的分布列为 Z 0 1 2 P 故 E（Z）0+1+2（12 分） 【点评】本题考查概率的计算，考查正态分布曲线的特点，考查数学期望，考查学生的 计算能力，属于中档题 第 20 页（共 24 页） 20 （12 分）已知椭圆 C 的中心在坐标原点 O，其右焦点为 F（1，0） ，以坐标原点 O 为圆 心，椭圆短半轴长为半径的圆与直线 xy+
42、0 的相切 （1）求椭圆 C 的方程； （2）经过点 F 的直线 l1，l2分别交椭圆 C 于 A、B 及 C、D 四点，且 l1l2，探究：是否 存在常数 ，使|AB|+|CD|AB|CD|恒成立 【分析】 （1）根据点到直线的距离可以求出短半轴长 b，因为焦点已知，所以 c1，根 据 a2b2+c2可以求得 a2，从而确定椭圆的方程； （2）分两类，l1，l2中一条斜率不存在，l1，l2的斜率存在且不为 0，分别来探索常 数 的值，其中在情形中，需要设 l1：xty+1（t0） ，然后联立 直线方程和椭圆的方程， 消去 x 得到关于 y 的方程， 再利用弦长公式分别求出|AB|和|CD|，
43、 并代入到化简即可得解 【解答】解： （1）设所求的椭圆方程为， 点 O 到直线 xy+0 的距离为， 又 c1，a2b2+c24， 故所求的椭圆 C 的方程为 （2）假设存在常数 ，使|AB|+|CD|AB|CD|恒成立，则， 当 l1， l2中一条斜率不存在时， 可知|AB|， |CD|其中一个长为 2a4， 另一个为， 此时， 当 l1，l2的斜率存在且不为 0 时，不妨设 l1：xty+1（t0） ， A（ty1+1，y1） ，B（ty2+1） ， 联立得（3t2+4）y2+6ty90， ，36t24（3t2+4） （9）144（t2+1） 0， 第 21 页（共 24 页） ， 用代
44、替上式中的 t 可得， ， 综上所述，存在常数使得|AB|+|CD|AB|CD|恒成立 【点评】本题考查直线与椭圆的位置关系，涉及点到直线的距离公式、曲直联立、弦长 公式，以及分类讨论的思想，考查学生的逻辑推理能力和运算能力，属于中档题 21 （12 分）已知函数 f（x）x2+ax+lnx（aR） （1）讨论函数 f（x）的单调性； （2）若 f（x）存在两个极值点 x1，x2且|x1x2|，求|f（x1）f（x2）|的最大值 【分析】 （1）求导可得，再分，讨论 f（x）与 0 的大小关系，进而得出单调性情况； （2）依题意，x1+x2a，x1x21，则，构 造函数，利用导数求其最大值即可 【解答】解： （1），设 （x）x2+ax+1，则 （0） 10，对称轴为， 当，即 a0 时，在（0，+）上，f（x）0，f（x）是增函数； 当，即 a0 时，a240 得 a2， （i）当2a0 时，在（0，+）上，f（x）0，f（x）是增函数； （ii）当 a2 时，令 f（x）0 得， 在上，f（x）0，f（x）是增函数；
