1、实数 2，0，2，中，为负数的是（ ） A2 B0 C2 D 2 （4 分）某自动控制器的芯片，可植入 2020000000 粒晶体管，这个数字 2020000000 用科 学记数法可表示为（ ） A0.2021010 B2.02109 C20.2108 D2.02108 3 （4 分）将如图的七巧板的其中几块，拼成一个多边形，为中心对称图形的是（ ） A B C D 4 （4 分）如图，点 A，B，C，D，E 均在O 上，BAC15，CED30，则BOD 的度数为（ ） A45 B60 C75 D90 5 （4 分）如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为 2：5，且三角
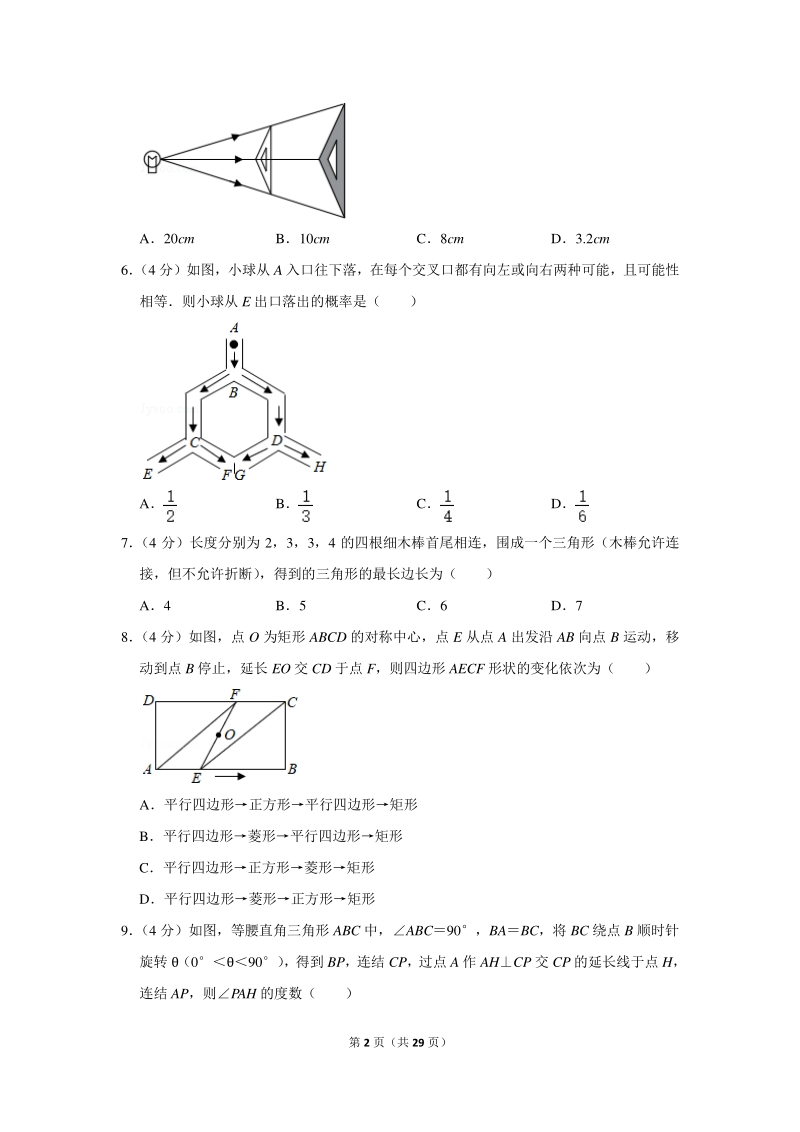
2、板的一边长为 8cm则投影三角板的对应边长为（ ） 第 2 页（共 29 页） A20cm B10cm C8cm D3.2cm 6 （4 分）如图，小球从 A 入口往下落，在每个交叉口都有向左或向右两种可能，且可能性 相等则小球从 E 出口落出的概率是（ ） A B C D 7 （4 分）长度分别为 2，3，3，4 的四根细木棒首尾相连，围成一个三角形（木棒允许连 接，但不允许折断） ，得到的三角形的最长边长为（ ） A4 B5 C6 D7 8 （4 分）如图，点 O 为矩形 ABCD 的对称中心，点 E 从点 A 出发沿 AB 向点 B 运动，移 动到点 B 停止，延长 EO 交 CD 于点
3、 F，则四边形 AECF 形状的变化依次为（ ） A平行四边形正方形平行四边形矩形 B平行四边形菱形平行四边形矩形 C平行四边形正方形菱形矩形 D平行四边形菱形正方形矩形 9 （4 分）如图，等腰直角三角形 ABC 中，ABC90，BABC，将 BC 绕点 B 顺时针 旋转 （090） ，得到 BP，连结 CP，过点 A 作 AHCP 交 CP 的延长线于点 H， 连结 AP，则PAH 的度数（ ） 第 3 页（共 29 页） A随着 的增大而增大 B随着 的增大而减小 C不变 D随着 的增大，先增大后减小 10 （4 分）同型号的甲、乙两辆车加满气体燃料后均可行驶 210km，它们各自单独行
4、驶并 返回的最远距离是 105km现在它们都从 A 地出发，行驶途中停下来从甲车的气体燃料 桶抽一些气体燃料注入乙车的气体燃料桶，然后甲车再行驶返回 A 地，而乙车继续行驶， 到 B 地后再行驶返回 A 地则 B 地最远可距离 A 地（ ） A120km B140km C160km D180km 二、填空题（本大题有二、填空题（本大题有 6 小题，每小题小题，每小题 5 分，共分，共 30 分）分） 11 （5 分）分解因式：1x2 12 （5 分）若关于 x，y 的二元一次方程组的解为则多项式 A 可以是 （写出一个即可） 13 （5 分）如图 1，直角三角形纸片的一条直角边长为 2，剪四块
5、这样的直角三角形纸片， 把它们按图 2 放入一个边长为 3 的正方形中（纸片在结合部分不重叠无缝隙） ，则图 2 中 阴影部分面积为 14 （5 分）如图，已知边长为 2 的等边三角形 ABC 中，分别以点 A，C 为圆心，m 为半径 作弧，两弧交于点 D，连结 BD若 BD 的长为 2，则 m 的值为 第 4 页（共 29 页） 15 （5 分）有两种消费券：A 券，满 60 元减 20 元，B 券，满 90 元减 30 元，即一次购物大 于等于 60 元、90 元，付款时分别减 20 元、30 元小敏有一张 A 券，小聪有一张 B 券， 他们都购了一件标价相同的商品，各自付款，若能用券时用
6、券，这样两人共付款 150 元， 则所购商品的标价是 元 16 （5 分）将两条邻边长分别为，1 的矩形纸片剪成四个等腰三角形纸片（无余纸片） ， 各种剪法剪出的等腰三角形中，其中一个等腰三角形的腰长可以是下列数中的 （填序号） ，1，1， 三、解答题（本大题有三、解答题（本大题有 8 小题，第小题，第 1720 小题每小题小题每小题 8 分，第分，第 21 小题小题 10 分，第分，第 22，23 小题每小题小题每小题 8 分，第分，第 24 小题小题 14 分，共分，共 80 分解答需写出必要的文字说明、演算步骤或证分解答需写出必要的文字说明、演算步骤或证 明过程）明过程） 17 （8 分
7、） （1）计算：4cos45+（1）2020 （2）化简： （x+y）2x（x+2y） 18 （8 分） 如图， 点 E 是ABCD 的边 CD 的中点， 连结 AE 并延长， 交 BC 的延长线于点 F （1）若 AD 的长为 2，求 CF 的长 （2）若BAF90，试添加一个条件，并写出F 的度数 19 （8 分）一只羽毛球的重量合格标准是 5.0 克5.2 克（含 5.0 克，不含 5.2 克） ，某厂对 4 月份生产的羽毛球重量进行抽样检验，并将所得数据绘制成如图统计图表 4 月份生产的羽毛球重量统计表 组别 重量 x（克） 数量（只） A x5.0 m 第 5 页（共 29 页） B
8、 5.0x5.1 400 C 5.1x5.2 550 D x5.2 30 （1）求表中 m 的值及图中 B 组扇形的圆心角的度数 （2）问这些抽样检验的羽毛球中，合格率是多少？如果购得 4 月份生产的羽毛球 10 筒 （每筒 12 只） ，估计所购得的羽毛球中，非合格品的羽毛球有多少只？ 20 （8 分）我国传统的计重工具秤的应用，方便了人们的生活如图 1，可以用秤砣到 秤纽的水平距离，来得出秤钩上所挂物体的重量称重时，若秤杆上秤砣到秤纽的水平 距离为 x（厘米）时，秤钩所挂物重为 y（斤） ，则 y 是 x 的一次函数下表中为若干次 称重时所记录的一些数据 x（厘米） 1 2 4 7 11
9、12 y（斤） 0.75 1.00 1.50 2.75 3.25 3.50 （1）在上表 x，y 的数据中，发现有一对数据记录错误在图 2 中，通过描点的方法， 观察判断哪一对是错误的？ （2）根据（1）的发现，问秤杆上秤砣到秤纽的水平距离为 16 厘米时，秤钩所挂物重是 多少？ 21 （10 分）如图 1 为搭建在地面上的遮阳棚，图 2、图 3 是遮阳棚支架的示意图遮阳棚 支架由相同的菱形和相同的等腰三角形构成，滑块 E，H 可分别沿等长的立柱 AB，DC 第 6 页（共 29 页） 上下移动，AFEFFG1m （1）若移动滑块使 AEEF，求AFE 的度数和棚宽 BC 的长 （2）当AFE
10、 由 60变为 74时，问棚宽 BC 是增加还是减少？增加或减少了多少？ （结果精确到 0.1m， 参考数据：1.73， sin370.60， cos370.80， tan370.75） 22 （12 分）问题：如图，在ABD 中，BABD在 BD 的延长线上取点 E，C，作AEC， 使 EAEC若BAE90，B45，求DAC 的度数 答案：DAC45 思考： （1）如果把以上“问题”中的条件“B45”去掉，其余条件不变，那么 DAC 的度数会改变吗？说明理由 （2）如果把以上“问题”中的条件“B45”去掉，再将“BAE90”改为“ BAEn” ，其余条件不变，求DAC 的度数 23 （12
11、分）如图 1，排球场长为 18m，宽为 9m，网高为 2.24m，队员站在底线 O 点处发球， 球从点 O 的正上方 1.9m 的 C 点发出， 运动路线是抛物线的一部分， 当球运动到最高点 A 时，高度为 2.88m，即 BA2.88m，这时水平距离 OB7m，以直线 OB 为 x 轴，直线 OC 为 y 轴，建立平面直角坐标系，如图 2 （1）若球向正前方运动（即 x 轴垂直于底线） ，求球运动的高度 y（m）与水平距离 x（m） 之间的函数关系式（不必写出 x 取值范围） 并判断这次发球能否过网？是否出界？说明 理由 （2） 若球过网后的落点是对方场地号位内的点 P （如图 1， 点 P
12、 距底线 1m， 边线 0.5m） ， 问发球点 O 在底线上的哪个位置？（参考数据：取 1.4） 第 7 页（共 29 页） 24 （14 分）如图 1，矩形 DEFG 中，DG2，DE3，RtABC 中，ACB90，CA CB2，FG，BC 的延长线相交于点 O，且 FGBC，OG2，OC4将ABC 绕点 O 逆时针旋转 （0180）得到ABC （1）当 30时，求点 C到直线 OF 的距离 （2）在图 1 中，取 AB的中点 P，连结 CP，如图 2 当 CP 与矩形 DEFG 的一条边平行时，求点 C到直线 DE 的距离 当线段 AP 与矩形 DEFG 的边有且只有一个交点时，求该交点
13、到直线 DG 的距离的 取值范围 第 8 页（共 29 页） 2020 年浙江省绍兴市中考数学试卷年浙江省绍兴市中考数学试卷 参考答案与试题解析参考答案与试题解析 一、选择题（本大题有一、选择题（本大题有 10 小题，每小题小题，每小题 4 分，共分，共 40 分请选出每小题中一个最符合题意分请选出每小题中一个最符合题意 的选项，不选、多选、错选，均不给分）的选项，不选、多选、错选，均不给分） 1 （4 分）实数 2，0，2，中，为负数的是（ ） A2 B0 C2 D 【分析】根据负数定义可得答案 【解答】解：实数 2，0，2，中，为负数的是2， 故选：C 【点评】此题主要考查了实数，关键是掌
14、握负数定义 2 （4 分）某自动控制器的芯片，可植入 2020000000 粒晶体管，这个数字 2020000000 用科 学记数法可表示为（ ） A0.2021010 B2.02109 C20.2108 D2.02108 【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相 同 【解答】解：20200000002.02109， 故选：B 【点评】此题考查科学记数法的表示方法，表示时关键要正确确定 a 的值以及 n 的值 3 （4 分）将如图的七巧板的其中几块，拼成一个多边形
15、，为中心对称图形的是（ ） A B C D 第 9 页（共 29 页） 【分析】根据中心对称的定义，结合所给图形即可作出判断 【解答】解：A、不是中心对称图形，故本选项不符合题意； B、不是中心对称图形，故本选项不符合题意； C、不是中心对称图形，故本选项不符合题意； D、是中心对称图形，故本选项符合题意 故选：D 【点评】本题考查了中心对称图形的特点，属于基础题，判断中心对称图形的关键是旋 转 180后能够重合 4 （4 分）如图，点 A，B，C，D，E 均在O 上，BAC15，CED30，则BOD 的度数为（ ） A45 B60 C75 D90 【分析】首先连接 BE，由圆周角定理即可得B
16、EC 的度数，继而求得BED 的度数， 然后由圆周角定理，求得BOD 的度数 【解答】解：连接 BE， BECBAC15，CED30， BEDBEC+CED45， BOD2BED90 故选：D 【点评】此题考查了圆周角定理注意准确作出辅助线是解此题的关键 5 （4 分）如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为 2：5，且三角 板的一边长为 8cm则投影三角板的对应边长为（ ） 第 10 页（共 29 页） A20cm B10cm C8cm D3.2cm 【分析】根据对应边的比等于相似比列式进行计算即可得解 【解答】解：设投影三角尺的对应边长为 xcm， 三角尺与投影三角尺相似
17、， 8：x2：5， 解得 x20 故选：A 【点评】本题主要考查相似三角形的应用利用数学知识解决实际问题是中学数学的重 要内容解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化 为数学问题 6 （4 分）如图，小球从 A 入口往下落，在每个交叉口都有向左或向右两种可能，且可能性 相等则小球从 E 出口落出的概率是（ ） A B C D 【分析】根据“在每个交叉口都有向左或向右两种可能，且可能性相等”可知在点 B、C、 D 处都是等可能情况，从而得到在四个出口 E、F、G、H 也都是等可能情况，然后概率 的意义列式即可得解 【解答】解：由图可知，在每个交叉口都有向左或向右两种可
18、能，且可能性相等， 小球最终落出的点共有 E、F、G、H 四个， 所以小球从 E 出口落出的概率是：； 故选：C 第 11 页（共 29 页） 【点评】本题考查了概率的求法，读懂题目信息，得出所给的图形的对称性以及可能性 相等是解题的关键，用到的知识点为：概率所求情况数与总情况数之比 7 （4 分）长度分别为 2，3，3，4 的四根细木棒首尾相连，围成一个三角形（木棒允许连 接，但不允许折断） ，得到的三角形的最长边长为（ ） A4 B5 C6 D7 【分析】利用三角形的三边关系列举出所围成三角形的不同情况，通过比较得到结论 【解答】解：长度分别为 5、3、4，能构成三角形，且最长边为 5；
19、长度分别为 2、6、4，不能构成三角形； 长度分别为 2、7、3，不能构成三角形； 综上所述，得到三角形的最长边长为 5 故选：B 【点评】本题考查了三角形的三边关系，利用了三角形中三边的关系求解注意分类讨 论，不重不漏 8 （4 分）如图，点 O 为矩形 ABCD 的对称中心，点 E 从点 A 出发沿 AB 向点 B 运动，移 动到点 B 停止，延长 EO 交 CD 于点 F，则四边形 AECF 形状的变化依次为（ ） A平行四边形正方形平行四边形矩形 B平行四边形菱形平行四边形矩形 C平行四边形正方形菱形矩形 D平行四边形菱形正方形矩形 【分析】根据对称中心的定义，根据矩形的性质，可得四边
20、形 AECF 形状的变化情况 【解答】解：观察图形可知，四边形 AECF 形状的变化依次为平行四边形菱形平行 四边形矩形 故选：B 【点评】考查了中心对称，矩形的性质，平行四边形的判定与性质，菱形的性质，根据 EF 与 AC 的位置关系即可求解 9 （4 分）如图，等腰直角三角形 ABC 中，ABC90，BABC，将 BC 绕点 B 顺时针 第 12 页（共 29 页） 旋转 （090） ，得到 BP，连结 CP，过点 A 作 AHCP 交 CP 的延长线于点 H， 连结 AP，则PAH 的度数（ ） A随着 的增大而增大 B随着 的增大而减小 C不变 D随着 的增大，先增大后减小 【分析】由
21、旋转的性质可得 BCBPBA，由等腰三角形的性质和三角形内接和定理可 求BPC+BPA135CPA， 由外角的性质可求PAH1359045， 即可 求解 【解答】解：将 BC 绕点 B 顺时针旋转 （090） ，得到 BP， BCBPBA， BCPBPC，BPABAP， CBP+BCP+BPC180， ABP+BAP+BPA180， ABP+CBP90， BPC+BPA135CPA， CPAAHC+PAH135， PAH1359045， PAH 的度数是定值， 故选：C 【点评】本题考查了旋转的性质，等腰三角形的性质，三角形的外角性质，灵活运用这 些性质解决问题是本题的关键 10 （4 分）同
22、型号的甲、乙两辆车加满气体燃料后均可行驶 210km，它们各自单独行驶并 返回的最远距离是 105km现在它们都从 A 地出发，行驶途中停下来从甲车的气体燃料 桶抽一些气体燃料注入乙车的气体燃料桶，然后甲车再行驶返回 A 地，而乙车继续行驶， 到 B 地后再行驶返回 A 地则 B 地最远可距离 A 地（ ） A120km B140km C160km D180km 【分析】设甲行驶到 C 地时返回，到达 A 地燃料用完，乙行驶到 B 地再返回 A 地时燃料 第 13 页（共 29 页） 用完，根据题意得关于 x 和 y 的二元一次方程组，求解即可 【解答】解：设甲行驶到 C 地时返回，到达 A
23、地燃料用完，乙行驶到 B 地再返回 A 地时 燃料用完，如图： 设 ABxkm，ACykm，根据题意得： ， 解得： 乙在 C 地时加注行驶 70km 的燃料，则 AB 的最大长度是 140km 故选：B 【点评】本题考查了二元一次方程组在行程问题中的应用，理清题中的数量关系正确列 出方程组是解题的关键 二、填空题（本大题有二、填空题（本大题有 6 小题，每小题小题，每小题 5 分，共分，共 30 分）分） 11 （5 分）分解因式：1x2 （1+x） （1x） 【分析】分解因式 1x2中，可知是 2 项式，没有公因式，用平方差公式分解即可 【解答】解：1x2（1+x） （1x） 故答案为：
24、（1+x） （1x） 【点评】本题考查了因式分解运用公式法，熟练掌握平方差公式的结构特点是解题的 关键 12 （5 分） 若关于 x， y 的二元一次方程组的解为则多项式 A 可以是 答 案不唯一，如 xy （写出一个即可） 【分析】根据方程组的解的定义，为应该满足所写方程组的每一个方程因此，可 以围绕为列一组算式，然后用 x，y 代换即可 【解答】解：关于 x，y 的二元一次方程组的解为， 而 110， 多项式 A 可以是答案不唯一，如 xy 故答案为：答案不唯一，如 xy 【点评】考查了二元一次方程组的解，本题是开放题，注意方程组的解的定义 第 14 页（共 29 页） 13 （5 分）如
25、图 1，直角三角形纸片的一条直角边长为 2，剪四块这样的直角三角形纸片， 把它们按图 2 放入一个边长为 3 的正方形中（纸片在结合部分不重叠无缝隙） ，则图 2 中 阴影部分面积为 4 【分析】根据题意和图形，可以得到直角三角形的一条直角边的长和斜边的长，从而可 以得到直角三角形的另一条直角边长，再根据图形，可知阴影部分的面积是四个直角三 角形的面积，然后代入数据计算即可 【解答】解：由题意可得， 直角三角形的斜边长为 3，一条直角边长为 2， 故直角三角形的另一条直角边长为：， 故阴影部分的面积是：4， 故答案为：4 【点评】本题考查正方形的性质、勾股定理、三角形的面积，解答本题的关键是明
26、确题 意，利用数形结合的思想解答 14 （5 分）如图，已知边长为 2 的等边三角形 ABC 中，分别以点 A，C 为圆心，m 为半径 作弧，两弧交于点 D，连结 BD若 BD 的长为 2，则 m 的值为 2 或 2 【分析】由作图知，点 D 在 AC 的垂直平分线上，得到点 B 在 AC 的垂直平分线上，求 得 BD 垂直平分 AC，设垂足为 E，得到 BE，当点 D、B 在 AC 的两侧时，如图，当 点 D、B 在 AC 的同侧时，如图，解直角三角形即可得到结论 【解答】解：由作图知，点 D 在 AC 的垂直平分线上， ABC 是等边三角形， 第 15 页（共 29 页） 点 B 在 AC
27、 的垂直平分线上， BD 垂直平分 AC， 设垂足为 E， ACAB2， BE， 当点 D、B 在 AC 的两侧时，如图， BD2， BEDE， ADAB2， m2； 当点 D、B 在 AC 的同侧时，如图， BD2， DE3， AD2， m2， 综上所述，m 的值为 2 或 2， 故答案为：2 或 2 【点评】本题考查了勾股定理，等边三角形的性质，线段垂直平分线的性质正确的作 出图形是解题的关键 15 （5 分）有两种消费券：A 券，满 60 元减 20 元，B 券，满 90 元减 30 元，即一次购物大 于等于 60 元、90 元，付款时分别减 20 元、30 元小敏有一张 A 券，小聪有
28、一张 B 券， 他们都购了一件标价相同的商品，各自付款，若能用券时用券，这样两人共付款 150 元， 则所购商品的标价是 100 或 85 元 第 16 页（共 29 页） 【分析】可设所购商品的标价是 x 元，根据小敏有一张 A 券，小聪有一张 B 券，他们都 购了一件标价相同的商品，各自付款，若能用券时用券，这样两人共付款 150 元，分 所购商品的标价小于 90 元；所购商品的标价大于 90 元；列出方程即可求解 【解答】解：设所购商品的标价是 x 元，则 所购商品的标价小于 90 元， x20+x150， 解得 x85； 所购商品的标价大于 90 元， x20+x30150， 解得 x
29、100 故所购商品的标价是 100 或 85 元 故答案为：100 或 85 【点评】考查了一元一次方程的应用，属于商品销售问题，注意分两种情况进行讨论求 解 16 （5 分）将两条邻边长分别为，1 的矩形纸片剪成四个等腰三角形纸片（无余纸片） ， 各种剪法剪出的等腰三角形中，其中一个等腰三角形的腰长可以是下列数中的 （填序号） ，1，1， 【分析】首先作出图形，再根据矩形的性质和等腰三角形的判定即可求解 【解答】解：如图所示： 第 17 页（共 29 页） 则其中一个等腰三角形的腰长可以是，1，1，不可以是 故答案为： 【点评】考查了矩形的性质，等腰三角形的判定与性质，根据题意作出图形是解题
30、的关 键 三、解答题（本大题有三、解答题（本大题有 8 小题，第小题，第 1720 小题每小题小题每小题 8 分，第分，第 21 小题小题 10 分，第分，第 22，23 小题每小题小题每小题 8 分，第分，第 24 小题小题 14 分，共分，共 80 分解答需写出必要的文字说明、演算步骤或证分解答需写出必要的文字说明、演算步骤或证 明过程）明过程） 17 （8 分） （1）计算：4cos45+（1）2020 （2）化简： （x+y）2x（x+2y） 【分析】 （1）直接利用特殊角的三角函数值以及二次根式的性质分别化简得出答案； （2）直接利用完全平方公式以及单项式乘以多项式运算法则计算得出答
31、案 【解答】解： （1）原式24+1 22+1 1； （2） （x+y）2x（x+2y） x2+2xy+y2x22xy y2 【点评】此题主要考查了实数运算以及完全平方公式以及单项式乘以多项式运算，正确 掌握相关运算法则是解题关键 18 （8 分） 如图， 点 E 是ABCD 的边 CD 的中点， 连结 AE 并延长， 交 BC 的延长线于点 F （1）若 AD 的长为 2，求 CF 的长 （2）若BAF90，试添加一个条件，并写出F 的度数 【分析】 （1）由平行四边形的性质得出 ADCF，则DAECFE，ADEFCE， 由点 E 是 CD 的中点，得出 DECE，由 AAS 证得ADEFC
32、E，即可得出结果； （2）添加一个条件当B60时，由直角三角形的性质即可得出结果（答案不唯一） 第 18 页（共 29 页） 【解答】解： （1）四边形 ABCD 是平行四边形， ADCF， DAECFE，ADEFCE， 点 E 是 CD 的中点， DECE， 在ADE 和FCE 中， ADEFCE（AAS） ， CFAD2； （2）BAF90， 添加一个条件：当B60时，F906030（答案不唯一） 【点评】本题考查了平行四边形的性质、全等三角形的判定与性质、平行线的性质、三 角形内角和定理等知识，熟练掌握全等三角形的判定与性质是解题的关键 19 （8 分）一只羽毛球的重量合格标准是 5.0
33、 克5.2 克（含 5.0 克，不含 5.2 克） ，某厂对 4 月份生产的羽毛球重量进行抽样检验，并将所得数据绘制成如图统计图表 4 月份生产的羽毛球重量统计表 组别 重量 x（克） 数量（只） A x5.0 m B 5.0x5.1 400 C 5.1x5.2 550 D x5.2 30 （1）求表中 m 的值及图中 B 组扇形的圆心角的度数 （2）问这些抽样检验的羽毛球中，合格率是多少？如果购得 4 月份生产的羽毛球 10 筒 （每筒 12 只） ，估计所购得的羽毛球中，非合格品的羽毛球有多少只？ 第 19 页（共 29 页） 【分析】 （1）图表中“C 组”的频数为 550 只，占抽查总
34、数的 55%，可求出抽查总数， 进而求出“A 组”的频数，即 m 的值；求出“B 组”所占总数的百分比，即可求出相应 的圆心角的度数； （2）计算“B 组” “C 组”的频率的和即为合格率，求出“不合格”所占的百分比，即 可求出不合格的数量 【解答】解： （1）55055%1000（只） ，10004005503020（只） 即：m20， 360144， 答：表中 m 的值为 20，图中 B 组扇形的圆心角的度数为 144； （2）+95%， 1210（195%）1205%6（只） ， 答：这次抽样检验的合格率是 95%，所购得的羽毛球中，非合格品的羽毛球有 6 只 【点评】考查统计表、扇形统
35、计图的意义和制作方法，理解图表中的数量和数量之间的 关系，是正确计算的前提 20 （8 分）我国传统的计重工具秤的应用，方便了人们的生活如图 1，可以用秤砣到 秤纽的水平距离，来得出秤钩上所挂物体的重量称重时，若秤杆上秤砣到秤纽的水平 距离为 x（厘米）时，秤钩所挂物重为 y（斤） ，则 y 是 x 的一次函数下表中为若干次 称重时所记录的一些数据 x（厘米） 1 2 4 7 11 12 y（斤） 0.75 1.00 1.50 2.75 3.25 3.50 （1）在上表 x，y 的数据中，发现有一对数据记录错误在图 2 中，通过描点的方法， 观察判断哪一对是错误的？ （2）根据（1）的发现，问
36、秤杆上秤砣到秤纽的水平距离为 16 厘米时，秤钩所挂物重是 多少？ 第 20 页（共 29 页） 【分析】 （1）利用描点法画出图形即可判断 （2）设函数关系式为 ykx+b，利用待定系数法解决问题即可 【解答】解： （1）观察图象可知：x7，y2.75 这组数据错误 （2）设 ykx+b，把 x1，y0.75，x2，y1 代入可得， 解得， yx+， 当 x16 时，y4.5， 答：秤杆上秤砣到秤纽的水平距离为 16 厘米时，秤钩所挂物重是 4.5 斤 【点评】本题考查一次函数的应用，待定系数法等知识，解题的关键是理解题意，灵活 运用所学知识解决问题 21 （10 分）如图 1 为搭建在地面
37、上的遮阳棚，图 2、图 3 是遮阳棚支架的示意图遮阳棚 支架由相同的菱形和相同的等腰三角形构成，滑块 E，H 可分别沿等长的立柱 AB，DC 上下移动，AFEFFG1m （1）若移动滑块使 AEEF，求AFE 的度数和棚宽 BC 的长 第 21 页（共 29 页） （2）当AFE 由 60变为 74时，问棚宽 BC 是增加还是减少？增加或减少了多少？ （结果精确到 0.1m， 参考数据：1.73， sin370.60， cos370.80， tan370.75） 【分析】 （1）根据等边三角形的性质得到AFE60，连接 MF 并延长交 AE 于 K，则 FM2FK，求得 FK，于是得到结论；
38、（2）解直角三角形即可得到结论 【解答】解： （1）AEEFAF1， AEF 是等边三角形， AFE60， 连接 MF 并延长交 AE 于 K，则 FM2FK， AEF 是等边三角形， AK， FK， FM2FK， BC4FM46.926.9（m） ； （2）AFE74， AFK37， KFAFcos370.80， FM2FK1.60， BC4FM6.406.92， 6.926.400.5， 答：当AFE 由 60变为 74时，棚宽 BC 是减少了，减少了 0.5m 第 22 页（共 29 页） 【点评】本题考查了解直角三角形的应用，菱形的性质，等边三角形的性质，正确的理 解题意是解题的关键
39、22 （12 分）问题：如图，在ABD 中，BABD在 BD 的延长线上取点 E，C，作AEC， 使 EAEC若BAE90，B45，求DAC 的度数 答案：DAC45 思考： （1）如果把以上“问题”中的条件“B45”去掉，其余条件不变，那么 DAC 的度数会改变吗？说明理由 （2）如果把以上“问题”中的条件“B45”去掉，再将“BAE90”改为“ BAEn” ，其余条件不变，求DAC 的度数 【分析】 （1）根据等腰三角形的性质得到AED2C，求得DAE90BAD 90（45+C）45C，由，即可得到结论； （2）设ABCm，根据三角形的内角和定理和等腰三角形的性质即可得到结论 【解答】解：
40、 （1）DAC 的度数不会改变； EAEC， AED2C， BAE90， BAD180（902C）45+C， DAE90BAD90（45+C）45C， 由，得，DACDAE+CAE45； （2）设ABCm， 则BAD（180m）90m，AEB180nm， 第 23 页（共 29 页） DAEnBADn90+m， EAEC， CAEAEB90nm， DACDAE+CAEn90+m+90nmn 【点评】本题考查了等腰三角形的性质，三角形的内角和定理，正确的识别图形是解题 的关键 23 （12 分）如图 1，排球场长为 18m，宽为 9m，网高为 2.24m，队员站在底线 O 点处发球， 球从点 O
41、 的正上方 1.9m 的 C 点发出， 运动路线是抛物线的一部分， 当球运动到最高点 A 时，高度为 2.88m，即 BA2.88m，这时水平距离 OB7m，以直线 OB 为 x 轴，直线 OC 为 y 轴，建立平面直角坐标系，如图 2 （1）若球向正前方运动（即 x 轴垂直于底线） ，求球运动的高度 y（m）与水平距离 x（m） 之间的函数关系式（不必写出 x 取值范围） 并判断这次发球能否过网？是否出界？说明 理由 （2） 若球过网后的落点是对方场地号位内的点 P （如图 1， 点 P 距底线 1m， 边线 0.5m） ， 问发球点 O 在底线上的哪个位置？（参考数据：取 1.4） 【分析
42、】 （1）求出抛物线表达式；再确定 x9 和 x18 时，对应函数的值即可求解； （2）当 y0 时，y（x7）2+2.880，解得：x19 或5（舍去5） ，求出 PQ 68.4，即可求解 【解答】解： （1）设抛物线的表达式为：ya（x7）2+2.88， 将 x0，y1.9 代入上式并解得：a， 故抛物线的表达式为：y（x7）2+2.88； 当 x9 时，y（x7）2+2.882.82.24， 第 24 页（共 29 页） 当 x18 时，y（x7）2+2.880.640， 故这次发球过网，但是出界了； （2）如图，分别过点作底线、边线的平行线 PQ、OQ 交于点 Q， 在 RtOPQ 中
43、，OQ18117， 当 y0 时，y（x7）2+2.880，解得：x19 或5（舍去5） ， OP19，而 OQ17， 故 PQ68.4， 98.40.50.1， 发球点 O 在底线上且距右边线 0.1 米处 【点评】本题考查的是二次函数综合运用，关键是弄清楚题意，明确变量的代表的实际 意义 24 （14 分）如图 1，矩形 DEFG 中，DG2，DE3，RtABC 中，ACB90，CA CB2，FG，BC 的延长线相交于点 O，且 FGBC，OG2，OC4将ABC 绕点 O 逆时针旋转 （0180）得到ABC （1）当 30时，求点 C到直线 OF 的距离 （2）在图 1 中，取 AB的中点
44、 P，连结 CP，如图 2 当 CP 与矩形 DEFG 的一条边平行时，求点 C到直线 DE 的距离 当线段 AP 与矩形 DEFG 的边有且只有一个交点时，求该交点到直线 DG 的距离的 取值范围 第 25 页（共 29 页） 【分析】 （1）如图 1 中，过点 C作 CHOF 于 H解直角三角形求出 CH 即可 （2）分两种情形：如图 2 中，当 CPOF 时，过点 C作 CMOF 于 M如图 3 中，当 CPDG 时，过点 C作 CNFG 于 N分别求出 CM，CN 即可 设 d 为所求的距离第一种情形：如图 4 中，当点 A落在 DE 上时，连接 OA，延 长 ED 交 OC 于 M如
45、图 5 中，当点 P 落在 DE 上时，连接 OP，过点 P 作 PQCB 于 Q结合图象可得结论 第二种情形： 当 AP 与 FG 相交， 不与 EF 相交时， 当点 A在 FG 上时， AG2 2，即 d22，如图 6 中，当点 P 落在 EF 上时，设 OF 交 AB于 Q，过点 P 作 PTBC于 T，过点 P 作 PROQ 交 OB于 R，连接 OP求出 QG 可得结论 第三种情形：当 AP 经过点 F 时，如图 7 中，显然 d3综上所述可得结论 【解答】解： （1）如图 1 中， 过点 C作 CHOF 于 H HCO30， CHCOcos302， 点 C到直线 OF 的距离为 2 第 26 页（共 29 页） （2）如图 2 中，当 CPOF 时，过点 C作 CMOF 于
