1、2020 年辽宁省沈阳市和平区中考数学二模试卷年辽宁省沈阳市和平区中考数学二模试卷 一选择题（共一选择题（共 10 小题）小题） 1地球平均半径约等于 6 400 000 米，6 400 000 用科学记数法表示为（ ） A64105 B6.4105 C6.4106 D6.4107 2估算面积为 3 的正方形的边长 b 的值（ ） A在 0 和 1 之间 B在 1 和 2 之间 C在 2 和 3 之间 D在 3 和 4 之间 3某几何体的三视图如图所示，该几何体是（ ） A圆锥 B圆柱 C三棱锥 D球 4不等式x+30 的正整数解有（ ） A1 个 B2 个 C3 个 D4 个 5一次函数 y
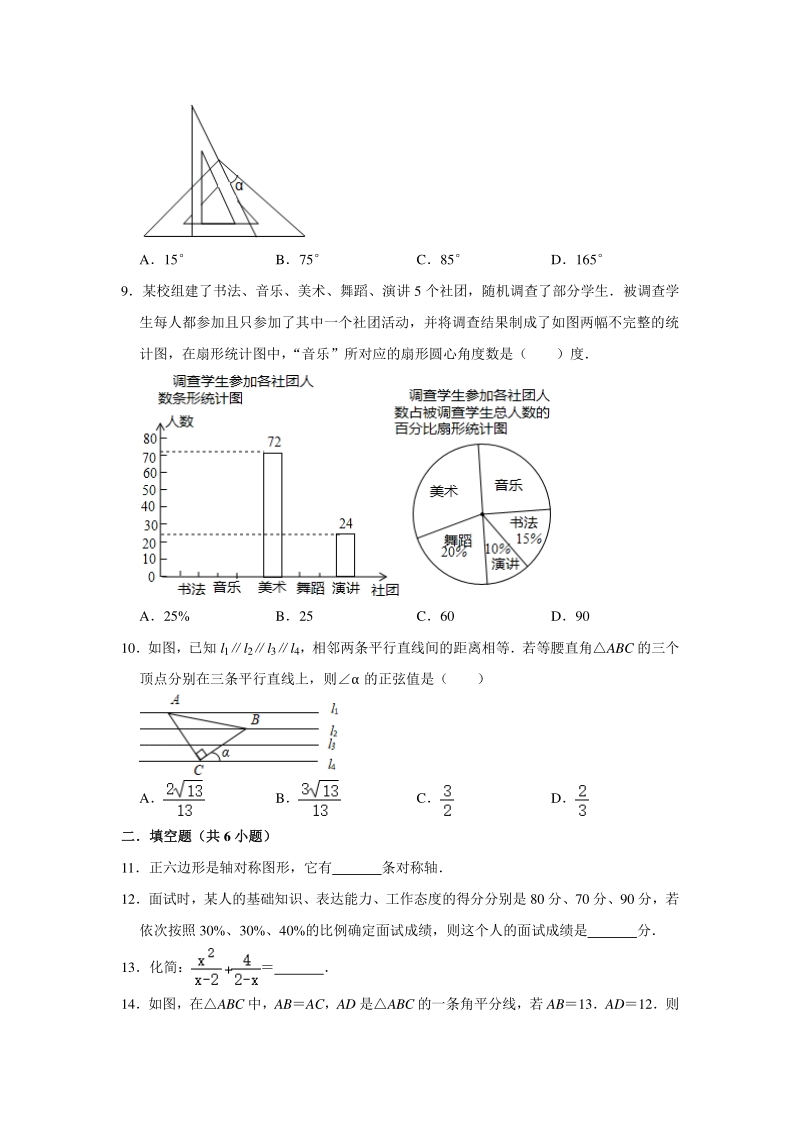
2、x2 的图象经过（ ） A第一、二、三象限 B第一、二、四象限 C第一、三、四象限 D第二、三、四象限 6下列运算正确的是（ ） Am2+m22m2 B （mn） （nm）n2m2 C （2mn）24m2n2 D （2m）3m32 7下列四种基本尺规作图分别表示：作一个角等于已知角；作一个角的平分线；过 直线外一点作已知直线的垂线； 作一条线段的垂直平分线， 则对应作法错误的是 （ ） A B C D 8将一副三角板如图叠放，则图中 余角的度数为（ ） A15 B75 C85 D165 9某校组建了书法、音乐、美术、舞蹈、演讲 5 个社团，随机调查了部分学生被调查学 生每人都参加且只参加了其中
3、一个社团活动，并将调查结果制成了如图两幅不完整的统 计图，在扇形统计图中， “音乐”所对应的扇形圆心角度数是（ ）度 A25% B25 C60 D90 10如图，已知 l1l2l3l4，相邻两条平行直线间的距离相等若等腰直角ABC 的三个 顶点分别在三条平行直线上，则 的正弦值是（ ） A B C D 二填空题（共二填空题（共 6 小题）小题） 11正六边形是轴对称图形，它有 条对称轴 12面试时，某人的基础知识、表达能力、工作态度的得分分别是 80 分、70 分、90 分，若 依次按照 30%、30%、40%的比例确定面试成绩，则这个人的面试成绩是 分 13化简： 14如图，在ABC 中，A
4、BAC，AD 是ABC 的一条角平分线，若 AB13AD12则 BC 的长为 15如图，在菱形 ABCD 中，对角线 AC 与 BD 相交于 O，且 AC8cm，BD6cm，则菱形 ABCD 的高 DE cm 16如图，在正方形 ABCD 中，AB16连接 AC，点 P 在线段 AC 上，PAAC，作射线 PM 与边 AB 相交于点 E将射线 PM 绕点 P 逆时针旋转 90得到射线 PN，射线 PN 与 边 BC 相交于点 F当AEP 的面积为时在边 CD 上取一点 G则AFG 周长的最 小值是 三解答题（共三解答题（共 9 小题）小题） 17计算：|16cos30|+（） 2（3）0 18
5、一个不透明的盒子中装有两个红球和一个蓝球这些球除颜色外都相同 （1）从中随机摸出一个球记下颜色后放回再从中随机摸出一个球 请用列表法或树状图法，求第一次摸到蓝球，第二次摸到红球的概率； 请直接写出两次摸到的球的颜色能配成紫色的概率 （2）从中随机摸出一个球，记下颜色后不放回再从中随机摸出一个球，请直接写出两 次摸到的球的颜色能配成紫色的概率 19如图，ABCD 中，A45，连接 BD，且 BDAD，点 E、点 F 分别是 AB、CD 上 的点，连接 EF 交 BD 于点 O，且 EFCD，BEDF1 （1）求 EF 的长； （2）直接写出ABCD 的面积 20 某校组织了一次比赛， 甲、 乙两
6、队各有 5 人参加比赛， 两队每人的比赛成绩 （单位： 分） 如下： 甲队：7，8，9，6，10 乙队：10，9，5，8，8 （1）甲队成绩的中位数是 分，乙队成绩的众数是 分； （2）计算乙队的平均成绩和方差； （3）已知甲队成绩的方差为 S2甲2，则成绩波动较大的是 队 21如图，AB 是O 的弦，直线 BC 与O 相切于点 B，ADBC，垂足为 D，连接 OA， OB （1）求证：AB 平分OAD； （2）当AOB100，O 的半径为 6cm 时 直接写出扇形 AOB 的面积约为 cm2（结果精确到 1cm2） ； 点 E 是O 上一动点（点 E 不与点 A、点 B 重合） ，连接 AE
7、，BE，请直接写出AEB 22某商店购进一批成本为每件 40 元的商品，若商店按单价不低于成本价，且不高于 70 元销售，且销售单价为正整数，经调查发现，该商品每天的销售量 y（件）与销售单价 x （元）之间的关系如表： 销售单价 x/元 40 50 60 70 每天的销售量y/件 140 120 100 80 （1）请你认真分析表中所给的数据，用你学过的一次函数、反比例函数和二次函数中的 一种来表示 y 与 x 之间的变化规律，说明选择这种函数的理由，并求出它的函数表达式 和自变量的取值范圈 （2）销售单价定为多少元时，才能使销售该商品每天获得的利润最大？最大利润是多少 元？ 23如图，在平
8、面立角坐标系中，反比例函数 y（k0，x0）与一次函数 yax+b 的 图象交于点 A（3，1） 、B（m，3） 点 C 的坐标为（1，0） ，连接 AC，BC （1）求反比例函数和一次函数的表达式； （2）当 x0 时，直接写出不等式ax+b 的解集 ； （3）若点 M 为 y 轴的正半轴上的动点，当ACM 是直角三角形时，直接写出点 M 的坐 标 24 （1）问题探究： 如图 1 所示，有公共顶点 A 的两个正方形 ABCD 和正方形 AEFGAEAB，连接 BE 与 DG，请判断线段 BE 与线段 DG 之间有怎样的数量关系和位置关系并请说明理由 （2）理解应用 如图 2 所示，有公共顶
9、点 A 的两个正方形 ABCD 和正方形 AEFG，AEAB，AB10，将 正方形 AEFG 绕点 A 在平面内任意旋转，当ABE15，且点 D、E、G 三点在同一条 直线上时，请直接写出 AE 的长 ； （3）拓展应用 如图 3 所示，有公共顶点 A 的两个矩形 ABCD 和矩形 AEFG，AD4，AB4， AG4，AE4，将矩形 AEFG 绕点 A 在平面内任意旋转，连接 BD，DE，点 M，N 分别是 BD，DE 的中点，连接 MN，当点 D、E、G 三点在同一条直线上时，请直接写出 MN 的长 25如图，在平面直角坐标系中，矩形 AOBC 的边 AO 在 x 轴的负半轴上，边 OB 在
10、 y 轴的 负半轴上且 AO12，OB9抛物线 yx2+bx+c 经过点 A 和点 B （1）求抛物线的表达式； （2）在第二象限的抛物线上找一点 M，连接 AM，BM，AB，当ABM 面积最大时，求 点 M 的坐标； （3）点 D 是线段 AO 上的动点，点 E 是线段 BO 上的动点，点 F 是射线 AC 上的动点， 连接 EF，DF，DE，BD，且 EF 是线段 BD 的垂直平分线当 CF1 时 直接写出点 D 的坐标 ； 若DEF 的面积为 30，当抛物线 yx2+bx+c 经过平移同时过点 D 和点 E 时，请直 接写出此时的抛物线的表达式 参考答案与试题解析参考答案与试题解析 一选
11、择题（共一选择题（共 10 小题）小题） 1地球平均半径约等于 6 400 000 米，6 400 000 用科学记数法表示为（ ） A64105 B6.4105 C6.4106 D6.4107 【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相 同当原数绝对值1 时，n 是正数；当原数的绝对值1 时，n 是负数 【解答】解：6 400 0006.4106， 故选：C 2估算面积为 3 的正方形的边长 b 的值（ ） A在 0 和 1 之间 B在 1 和 2 之间 C在 2
12、 和 3 之间 D在 3 和 4 之间 【分析】根据正方形的面积公式可得面积为 3 的正方形的边长 b 的值为，因为 1 2，由此可以得到 b 的值的范围 【解答】解：面积为 3 的正方形的边长 b 的值为， 12， 实数的值在整数 1 和 2 之间 故选：B 3某几何体的三视图如图所示，该几何体是（ ） A圆锥 B圆柱 C三棱锥 D球 【分析】由已知三视图得到几何体是圆锥 【解答】解：由已知三视图得到几何体是以圆锥； 故选：A 4不等式x+30 的正整数解有（ ） A1 个 B2 个 C3 个 D4 个 【分析】先求出不等式的解集，然后根据不等式的解集求其整数解 【解答】解：不等式x+30
13、的解集是 x3， 不等式的正整数解是 1，2，3， 故选：C 5一次函数 yx2 的图象经过（ ） A第一、二、三象限 B第一、二、四象限 C第一、三、四象限 D第二、三、四象限 【分析】根据一次函数 ykx+b（k0）中的 k、b 判定该函数图象所经过的象限 【解答】解：10， 一次函数 yx2 的图象一定经过第二、四象限； 又20， 一次函数 yx2 的图象与 y 轴交于负半轴， 一次函数 yx2 的图象经过第二、三、四象限； 故选：D 6下列运算正确的是（ ） Am2+m22m2 B （mn） （nm）n2m2 C （2mn）24m2n2 D （2m）3m32 【分析】根据合并同类项、平
14、方差公式、积的乘方、同底数幂的除法分别计算即可 【解答】解：A、m2+m22m2，原计算正确，故此选项符合题意； B、 （mn） （nm）（n2mn+m2） ，原计算错误，故此选项不符合题意； C、 （2mn）24m2n2，原计算错误，故此选项不符合题意； D、 （2m）3m38m3m38，原计算错误，故此选项不符合题意 故选：A 7下列四种基本尺规作图分别表示：作一个角等于已知角；作一个角的平分线；过 直线外一点作已知直线的垂线； 作一条线段的垂直平分线， 则对应作法错误的是 （ ） A B C D 【分析】根据作一个角等于已知角；作一个角的平分线；作一条线段的垂直平分线；过 直线外一点 P
15、 作已知直线的垂线的作法，即可判断得出答案 【解答】解：作一个角等于已知角的方法正确； 作一个角的平分线的作法正确； 过直线外一点 P 作已知直线的垂线的作法正确； 作一条线段的垂直平分线，两弧缺少另一个交点，作法错误； 故选：D 8将一副三角板如图叠放，则图中 余角的度数为（ ） A15 B75 C85 D165 【分析】根据三角形的外角的性质计算即可 【解答】解：由三角形的外角的性质可知，604515， 所以 的余角为 75， 故选：B 9某校组建了书法、音乐、美术、舞蹈、演讲 5 个社团，随机调查了部分学生被调查学 生每人都参加且只参加了其中一个社团活动，并将调查结果制成了如图两幅不完整
16、的统 计图，在扇形统计图中， “音乐”所对应的扇形圆心角度数是（ ）度 A25% B25 C60 D90 【分析】根据演讲的人数和所占的百分比求出调查的总人数，再求出美术、音乐所占的 百分比，然后用 360乘以音乐所占的百分比即可得出答案 【解答】解：调查的总人数有：2410%240（人） ， 美术所占的百分比是：100%30%， 则音乐所占的百分比是：115%10%20%30%25%， 则， “音乐”所对应的扇形圆心角度数是 36025%90； 故选：D 10如图，已知 l1l2l3l4，相邻两条平行直线间的距离相等若等腰直角ABC 的三个 顶点分别在三条平行直线上，则 的正弦值是（ ） A
17、 B C D 【分析】过点 A 作 ADl4于 D，过点 B 作 BEl4于 E，根据同角的余角相等求出CAD BCE，然后利用“角角边”证明ACD 和CBE 全等，根据全等三角形对应边相等 可得 CEAD，然后利用勾股定理列式求出 BC，然后利用锐角的正弦等于对边比斜边列 式计算即可得解 【解答】解：如图，过点 A 作 ADl4于 D，过点 B 作 BEl4于 E，设 l1，l2，l3，l4间 的距离为 1， CAD+ACD90， BCE+ACD90， CADBCE， 在等腰直角ABC 中，ACBC， 在ACD 和CBE 中， ， ACDCBE（AAS） ， CEAD3， 在 RtBCE 中
18、，BC， sin 故选：A 二填空题（共二填空题（共 6 小题）小题） 11正六边形是轴对称图形，它有 6 条对称轴 【分析】根据轴对称图形的特点可直接求解 【解答】解：正六边形有 6 条对称轴，分别是 3 条对角线和三组对边的垂直平分线 正六边形是轴对称图形，它有 6 条对称轴 12面试时，某人的基础知识、表达能力、工作态度的得分分别是 80 分、70 分、90 分，若 依次按照 30%、30%、40%的比例确定面试成绩，则这个人的面试成绩是 81 分 【分析】根据加权平均数定义可得 【解答】解：这个人的面试成绩是 8030%+7030%+9040%81（分） 故答案为：81 13化简： x
19、+2 【分析】先转化为同分母（x2）的分式相加减，然后约分即可得解 【解答】解：+ x+2 故答案为：x+2 14如图，在ABC 中，ABAC，AD 是ABC 的一条角平分线，若 AB13AD12则 BC 的长为 10 【分析】先根据等腰三角形的性质得出 BC2BD，再由勾股定理求出 BD 的长，进而可 得出结论 【解答】解：在ABC 中，ABAC13，AD 是角平分线，AD12， BC2BD，ADBC 在 RtABD 中，BD2+AD2AB2， 即 BD2+122132， 解得 BD5， BC10 故答案为：10 15如图，在菱形 ABCD 中，对角线 AC 与 BD 相交于 O，且 AC8
20、cm，BD6cm，则菱形 ABCD 的高 DE 4.8 cm 【分析】根据菱形的面积公式得出其面积，再利用勾股定理得出 AB 的长，进而得出 DE 即可 【解答】解：在菱形 ABCD 中，对角线 AC 与 BD 相交于 O，且 AC8cm，BD6cm， 菱形的面积24cm2， 四边形 ABCD 是菱形， ACBD，OA4cm，OD3cm， AD， AB5cm， 菱形的面积ABDE24cm2， DEcm， 故答案为：4.8 16如图，在正方形 ABCD 中，AB16连接 AC，点 P 在线段 AC 上，PAAC，作射线 PM 与边 AB 相交于点 E将射线 PM 绕点 P 逆时针旋转 90得到射
21、线 PN，射线 PN 与 边 BC 相交于点 F当AEP 的面积为时在边 CD 上取一点 G则AFG 周长的最 小值是 + 【分析】如图，作点 G 关于点 C 的对称点 H，连接 AH，GH，过点 P 作 PKBC 于 K， PJAB 于 J利用三角形的面积公式求出 AE，再利用相似三角形的性质求出 KF，利用 勾股定理求出 AF，AH，QCAG+GF 的最小值即可解决问题 【解答】解：如图，作点 G 关于点 C 的对称点 H，连接 AH，GH，过点 P 作 PKBC 于 K，PJAB 于 J 四边形 ABCD 是正方形，AB16， ACAB16， PAAC， PA4， PJAJ，PAJ45，
22、 PJAJ4，BJ16412， PKBC， BPJBPKB90， 四边形 PJBK 是矩形， PKBJ12， SPAEAEPJ， AE，EJ4， JPKMPN90， JPEFPK， PJEPKF90， PJEPKF， ， ， FK，CF12+，BF， BH+16， AF，AH ， GFGH， AG+FGAG+GH， AG+GHAH， AG+GH， GA+FG 的最小值为， AFG 的周长的最小值为+ 故答案为+ 三解答题（共三解答题（共 9 小题）小题） 17计算：|16cos30|+（） 2（3）0 【分析】直接利用特殊角的三角函数值以及负整数指数幂的性质、零指数幂的性质分别 化简得出答案
23、【解答】解：原式|16|3+41 313+41 2 18一个不透明的盒子中装有两个红球和一个蓝球这些球除颜色外都相同 （1）从中随机摸出一个球记下颜色后放回再从中随机摸出一个球 请用列表法或树状图法，求第一次摸到蓝球，第二次摸到红球的概率； 请直接写出两次摸到的球的颜色能配成紫色的概率 （2）从中随机摸出一个球，记下颜色后不放回再从中随机摸出一个球，请直接写出两 次摸到的球的颜色能配成紫色的概率 【分析】 （1）根据题意画出树状图得出所有等情况数，找出第一次摸到蓝球，第二次 摸到红球的情况数，然后根据概率公式即可得出答案； 找出两次摸到的球的颜色能配成紫色的情况数，再根据概率公式即可得出答案；
24、 （2） 根据题意画出树状图得出所有等情况数和两次摸到的球的颜色能配成紫色的情况数， 然后根据概率公式即可得出答案 【解答】解： （1）根据题意画图如下： 共有 9 种等情况数，其中第一次摸到蓝球，第二次摸到红球的有 2 种， 则第一次摸到蓝球，第二次摸到红球的概率是； 两次摸到的球的颜色能配成紫色的有 4 种情况， 则两次摸到的球的颜色能配成紫色的概率是； 故答案为：； （2）根据题意画图如下： 共有 6 种等情况数，其中两次摸到的球的颜色能配成紫色的有 4 种， 则两次摸到的球的颜色能配成紫色的概率； 故答案为： 19如图，ABCD 中，A45，连接 BD，且 BDAD，点 E、点 F 分
25、别是 AB、CD 上 的点，连接 EF 交 BD 于点 O，且 EFCD，BEDF1 （1）求 EF 的长； （2）直接写出ABCD 的面积 8 【分析】 （1）根据平行四边形的性质和等腰直角三角形的性质解答即可； （2）根据等腰直角三角形的性质和平行四边形的面积公式解答即可 【解答】解： （1）A45，BDAD， ABD 是等腰直角三角形， DBA45，ADDB， 四边形 ABCD 是平行四边形， CDAB， EFCD， EFAB， OEB 是等腰直角三角形，DFO 是等腰直角三角形， DFBE1， OEBE1，OFDF1， EF2； （2）OEB 和DFO 是等腰直角三角形， OEEBOF
26、DF1， ODOB， DB2， ADB 是等腰直角三角形， AB， ABCD 的面积ABEF428 故答案为：8 20 某校组织了一次比赛， 甲、 乙两队各有 5 人参加比赛， 两队每人的比赛成绩 （单位： 分） 如下： 甲队：7，8，9，6，10 乙队：10，9，5，8，8 （1）甲队成绩的中位数是 8 分，乙队成绩的众数是 8 分； （2）计算乙队的平均成绩和方差； （3）已知甲队成绩的方差为 S2甲2，则成绩波动较大的是 乙 队 【分析】 （1）根据中位数、众数的定义直接求解即可； （2）根据平均数、方差的计算方法，先计算乙队的平均数，再求乙队的方差； （3）根据两队方差的大小，判断两队
27、成绩波动的大小 【解答】解： （1）甲队比赛成绩按从小到大顺序排列为 6，7，8，9，10，其中位数为 8； 乙队成绩中 8 出现了 2 次，故乙队的众数是 8 故答案为：8，8； （2）乙队的平均成绩为（10+9+5+8+8）8， 其方差 S2乙（108）2+（98）2+（58）2+（88）2+（88）2 142.8 答：乙队成绩的平均成绩为 8 分，乙队成绩的方差为 2.5； （3）22.8，即 S2甲S2乙， 乙队成绩波动较大 故答案为：乙 21如图，AB 是O 的弦，直线 BC 与O 相切于点 B，ADBC，垂足为 D，连接 OA， OB （1）求证：AB 平分OAD； （2）当AOB
28、100，O 的半径为 6cm 时 直接写出扇形 AOB 的面积约为 31 cm2（结果精确到 1cm2） ； 点 E 是O 上一动点（点 E 不与点 A、点 B 重合） ，连接 AE，BE，请直接写出AEB 50 或 130 【分析】 （1）根据 OAOB，可以得到OBAOAB，再根据平行线的性质可以得到 OBADAB，然后即可得到结论成立； （2）根据扇形面积的计算公式，可以求得扇形 AOB 的面积； 根据圆周角定理，利用分类讨论的方法，可以得到AEB 的度数 【解答】 （1）证明：OAOB， OBAOAB， OBCB，ADBC， OBAD， OBADAB， OABDAB， AB 平分OAD
29、； （2）AOB100，O 的半径为 6cm， 扇形 AOB 的面积为：31（cm2） ， 故答案为：31； 当点 E 在优弧 AB 上时， AOB100， AEB50， 当点 E 在劣弧 AB 上室， AEB18050130， 故答案为：50 或 130 22某商店购进一批成本为每件 40 元的商品，若商店按单价不低于成本价，且不高于 70 元销售，且销售单价为正整数，经调查发现，该商品每天的销售量 y（件）与销售单价 x （元）之间的关系如表： 销售单价 x/元 40 50 60 70 每天的销售量y/件 140 120 100 80 （1）请你认真分析表中所给的数据，用你学过的一次函数、
30、反比例函数和二次函数中的 一种来表示 y 与 x 之间的变化规律，说明选择这种函数的理由，并求出它的函数表达式 和自变量的取值范圈 （2）销售单价定为多少元时，才能使销售该商品每天获得的利润最大？最大利润是多少 元？ 【分析】 （1）表格数据符合一次函数的规律，故设函数的表达式为：ykx+b，将（40， 140） 、 （50，120）代入上式，即可求解； （2）设该商品每天获得的利润为 w，则 wy（x40） ，即可求解 【解答】解： （1）表格数据符合一次函数的规律，故设函数的表达式为：ykx+b， 将（40，140） 、 （50，120）代入上式得：，解得：， 故函数的表达式为：y2x+2
31、20（40x70） ； （2）设该商品每天获得的利润为 w，则 wy（x40）（2x+200） （x40）2 （x100） （x40） （40x70） ； 20，故 w 有最大值， 当 x（100+40）70 时，w 最大值，最大值为 1800， 故销售单价定为 70 元时，销售该商品每天获得的利润最大，最大利润是 1800 元 23如图，在平面立角坐标系中，反比例函数 y（k0，x0）与一次函数 yax+b 的 图象交于点 A（3，1） 、B（m，3） 点 C 的坐标为（1，0） ，连接 AC，BC （1）求反比例函数和一次函数的表达式； （2）当 x0 时，直接写出不等式ax+b 的解集
32、1x0 或 x3 ； （3）若点 M 为 y 轴的正半轴上的动点，当ACM 是直角三角形时，直接写出点 M 的坐 标 （0，13）或（0，） 【分析】 （1）用待定系数法即可求解； （2）观察函数图象即可求解； （3）分 MC 是斜边、CA 是斜边、AM 是斜边三种情况，分别求解即可 【解答】解： （1）将点 A 的坐标代入反比例函数表达式得：1，解得：k3， 将点 B 的坐标代入反比例函数表达式并解得：m1，故点 B（1，3） ， 将点 A、B 的坐标代入一次函数表达式得：，解得， 故反比例函数和一次函数的表达式分别为：y，yx+4； （2）观察函数图象得，当 x0 时，x1 或 x3 时，
33、不等式ax+b 成立， 即不等式的解集为：1x0 或 x3， 故答案为：1x0 或 x3； （3）设点 M（0，m） （m0） ，点 C（1，0） 、A（3，1） ， 则 MC21+m2，CA2（1+3）2+117，AM29+（m1）2， 当 MC 是斜边时，则 1+m217+9+（m1）2，解得：m13； 当 CA 是斜边时，同理可得：m（负值已舍去） ； 当 AM 是斜边时，同理可得：m4（舍去） ； 故答案为（0，13）或（0，） 24 （1）问题探究： 如图 1 所示，有公共顶点 A 的两个正方形 ABCD 和正方形 AEFGAEAB，连接 BE 与 DG，请判断线段 BE 与线段 D
34、G 之间有怎样的数量关系和位置关系并请说明理由 （2）理解应用 如图 2 所示，有公共顶点 A 的两个正方形 ABCD 和正方形 AEFG，AEAB，AB10，将 正方形 AEFG 绕点 A 在平面内任意旋转，当ABE15，且点 D、E、G 三点在同一条 直线上时，请直接写出 AE 的长 55 ； （3）拓展应用 如图 3 所示，有公共顶点 A 的两个矩形 ABCD 和矩形 AEFG，AD4，AB4， AG4，AE4，将矩形 AEFG 绕点 A 在平面内任意旋转，连接 BD，DE，点 M，N 分别是 BD，DE 的中点，连接 MN，当点 D、E、G 三点在同一条直线上时，请直接写出 MN 的长
35、 6或 8 【分析】 （1）由“SAS”可证GADEAB，可得 BEDG，ADGABE，由直角 三角形的性质可得 BEDG； （2）由“SAS”可证GADEAB，可得 BEDG，ADGABE15，可得 DEB90，由直角三角形的性质可求解； （3） 分两种情况讨论， 通过证明AGDAEB， 可得， DGAAEB， 由勾股定理和三角形中位线定理可求解 【解答】解： （1）BEDG，BEDG， 理由如下：如图 1：延长 BE 交 AD 于 N，交 DG 于 H， 四边形 ABCD 是正方形，四边形 AEFG 是正方形， AGAE，ABAD，GAEDAB90， GADEAB， GADEAB（SAS）
36、 ， BEDG，ADGABE， ABE+ANB90， ADG+DNH90， DHN90， BEDG； （2）如图，当点 G 在线段 DE 上时，连接 BD， 四边形 ABCD 是正方形，四边形 AEFG 是正方形， AGAE，ABAD10，GAEDAB90，ADB45ABD，BDAB 10，GEAE， GADEAB， GADEAB（SAS） ， BEDG，ADGABE15， BDE451530，DBE45+1560， DEB90， BEBD5DG，DEBE5， GE55， AE55， 当点 E 在线段 DG 上时， 同理可求 AE55， 故答案为：55； （3）如图，若点 G 在线段 DE 上
37、时， AD4，AB4，AG4，AE4， DB8，GE8， DABGAE90， DAGBAE， 又， AGDAEB， ，DGAAEB， BEDG， DGAGAE+DEA，AEBDEB+AED， GAEDEB90， DB2DE2+BE2， 6413（DG+8）2+3DG2， DG12 或 DG16（舍去） ， BE12， 点 M，N 分别是 BD，DE 的中点， MNBE6； 如图，当点 E 在线段 DG 上时， 同理可求：BE16， 点 M，N 分别是 BD，DE 的中点， MNBE8， 综上所述：MN 为 6或 8， 故答案为：6或 8 25如图，在平面直角坐标系中，矩形 AOBC 的边 AO
38、 在 x 轴的负半轴上，边 OB 在 y 轴的 负半轴上且 AO12，OB9抛物线 yx2+bx+c 经过点 A 和点 B （1）求抛物线的表达式； （2）在第二象限的抛物线上找一点 M，连接 AM，BM，AB，当ABM 面积最大时，求 点 M 的坐标； （3）点 D 是线段 AO 上的动点，点 E 是线段 BO 上的动点，点 F 是射线 AC 上的动点， 连接 EF，DF，DE，BD，且 EF 是线段 BD 的垂直平分线当 CF1 时 直接写出点 D 的坐标 （12+3，0）或（3，0） ； 若DEF 的面积为 30，当抛物线 yx2+bx+c 经过平移同时过点 D 和点 E 时，请直 接写
39、出此时的抛物线的表达式 yx2x4 【分析】 （1）利用待定系数法把问题转化为解方程组即可解决问题 （2）如图 1 中，设 M（m，m2m9） ，根据 SABMSACM+SMBCSACB构建 二次函数，利用二次函数的性质解决问题即可 （3）分两种情形：如图 2 中，当点 F 在 AC 的延长线设时，连接 DF，FB设 D（m， 0） 根据 FDFB，构建方程求解当点 F 在线段 AC 上时，同法可得 根据三角形的面积求出 D，E 的坐标，再利用待定系数法解决问题即可 【解答】解： （1）由题意 A（12，0） ，B（0，9） ， 把 A，B 的坐标代入 yx2+bx+c 得到， 解得， 抛物线
40、的解析式为 yx2x9 （2）如图 1 中，设 M（m，m2m9） ， SABMSACM+SMBCSACB9 （m+12） +12 （m2m9+9） 1296m272m6（m+6）2+216， 60， m6 时，ABM 的面积最大，此时 M（6，31.5） （3）如图 2 中，当点 F 在 AC 的延长线设时，连接 DF，FB设 D（m，0） EF 垂直平分线段 BD， FDFB， F（12，10） ，B（0，9） ， 102+（m+12）2122+12， m123（舍弃）或12+3， D（12+3，0） 当点 F 在线段 AC 上时，同法可得 D（3，0） ， 综上所述，满足条件的点 D 的坐标为（12+3，0）或（3，0） 故答案为（12+3，0）或（3，0） 由可知EF 的面积为 30， D（3，0） ，E（0，4） ， 把 D，E 代入 yx2+bx+c，可得， 解得， 抛物线的解析式为 yx2x4 故答案为 yx2x4
