1、书书书 届普通高中名校联考信息卷（ 压轴卷一） （ 高考研究卷） 文科数学 考生注意： 本试卷共 分， 考试时间 分钟 请将答案填在答题卡上 一、 选择题： 本大题共 小题， 每小题分， 共 分 在每小题给出的四个选项中， 只有一项是 符合题目要求的 设函数狔 狓 槡 的定义域为犃， 函数狔 （ 狓） 的定义域为犅 ， 则 犃犅 （ ） （，）（，） ，） 若复数狕满足（ ）狕 ， 则 珔狕 （ ） 槡 槡 等于 （ ） 槡 槡 聊斋志异 中有： “ 挑水砍柴不堪苦， 请归但求穿墙术”在数学中， 我们称形如以下形式的等 式具有“ 穿墙术” ： 槡 槡 ， 槡 槡 ， 槡 槡 ， 则按照以上规律
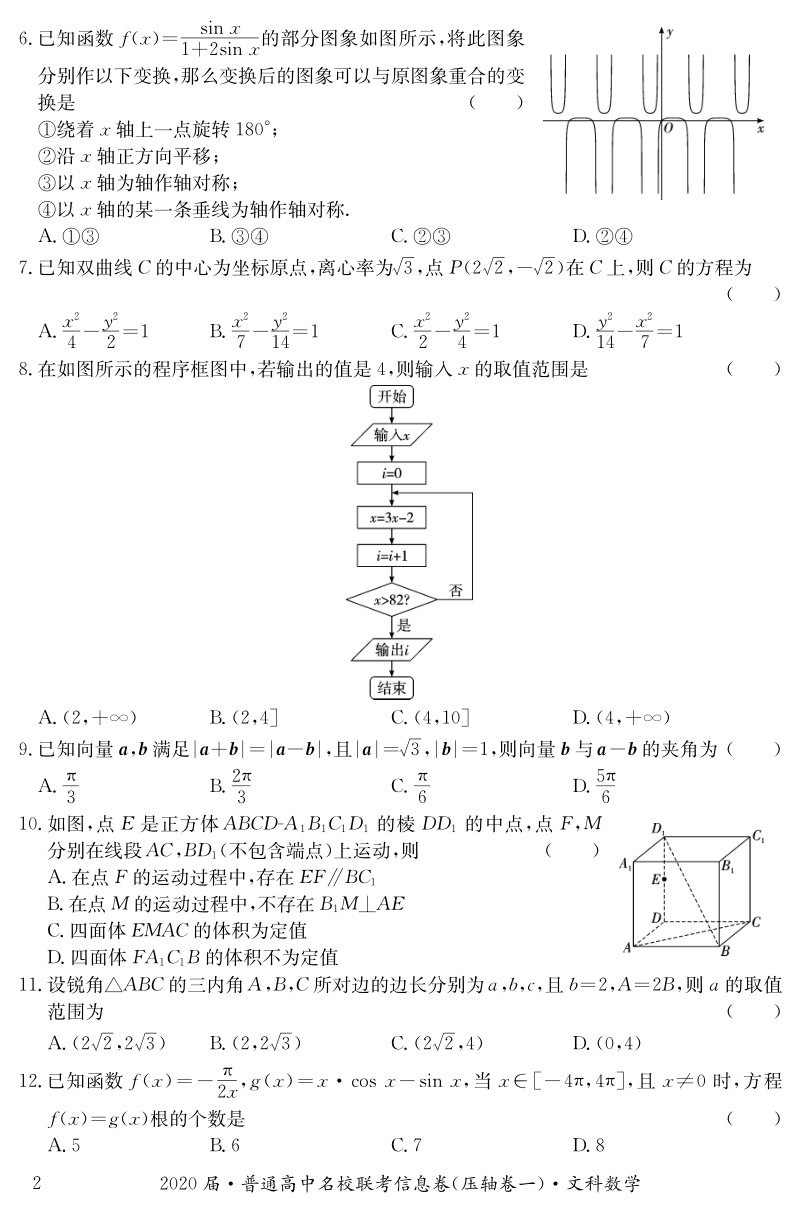
2、， 若 犿槡 犿 狀 犿 槡 犿 狀 具有“ 穿墙术” ， 则犿，狀满足的关系式为（ ） 狀 犿 狀 （犿 ）狀（犿 ） 狀犿 某四棱锥的三视图如图所示， 记犛为此棱锥所有棱的长度的集合， 则 （ ） 槡犛， 且槡犛 槡犛， 且槡犛 槡犛， 且槡犛 槡犛， 且槡犛 届普通高中名校联考信息卷（ 压轴卷一） 文科数学 已知函数犳（ 狓） 狓 狓的部分图象如图所示， 将此图象 分别作以下变换， 那么变换后的图象可以与原图象重合的变 换是（ ） 绕着狓轴上一点旋转 ； 沿狓轴正方向平移； 以狓轴为轴作轴对称； 以狓轴的某一条垂线为轴作轴对称 已知双曲线犆的中心为坐标原点， 离心率为槡 ， 点 犘（槡，
3、槡 ） 在 犆上， 则犆的方程为 （ ） 狓 狔 狓 狔 狓 狔 狔 狓 在如图所示的程序框图中， 若输出的值是， 则输入狓的取值范围是 （ ） （，）（，（， （，） 已知向量犪， 犫满足犪犫 犪犫 ， 且 犪 槡 ，犫 ， 则向量犫与犪犫的夹角为 （ ） 如图， 点犈是正方体犃 犅 犆 犇 犃犅 犆犇的棱犇 犇的中点， 点犉，犕 分别在线段犃 犆，犅 犇（ 不包含端点） 上运动， 则（ ） 在点犉的运动过程中， 存在犈 犉犅 犆 在点犕的运动过程中， 不存在犅犕犃 犈 四面体犈犕犃 犆的体积为定值 四面体犉 犃犆 犅的体积不为定值 设锐角犃 犅 犆的三内角犃， 犅，犆所对边的边长分别为犪，
4、犫，犮 ， 且 犫 ，犃 犅 ， 则 犪的取值 范围为（ ） （槡，槡）（，槡）（槡，）（，） 已知函数犳（狓） 狓， 犵（狓）狓 狓 狓， 当狓 ， ， 且 狓时， 方程 犳（狓）犵（狓） 根的个数是 （ ） 届普通高中名校联考信息卷（ 压轴卷一） 文科数学 二、 填空题： 本大题共小题， 每小题分， 共 分 把答案填在答题卡相应位置上 若函数犳（狓） 狓，狓 ， 犪 狓 犫，狓 烅 烄 烆 ， 且犳（） ， 犳（ ） ， 则 犳（犳（ ） ） 将一颗骰子先后投掷两次分别得到点数犪，犫， 则直线犪 狓 犫 狔 与圆（ 狓 ） 狔 有公 共点的概率为 圆锥底面半径为， 高为槡 ， 点 犘是底面
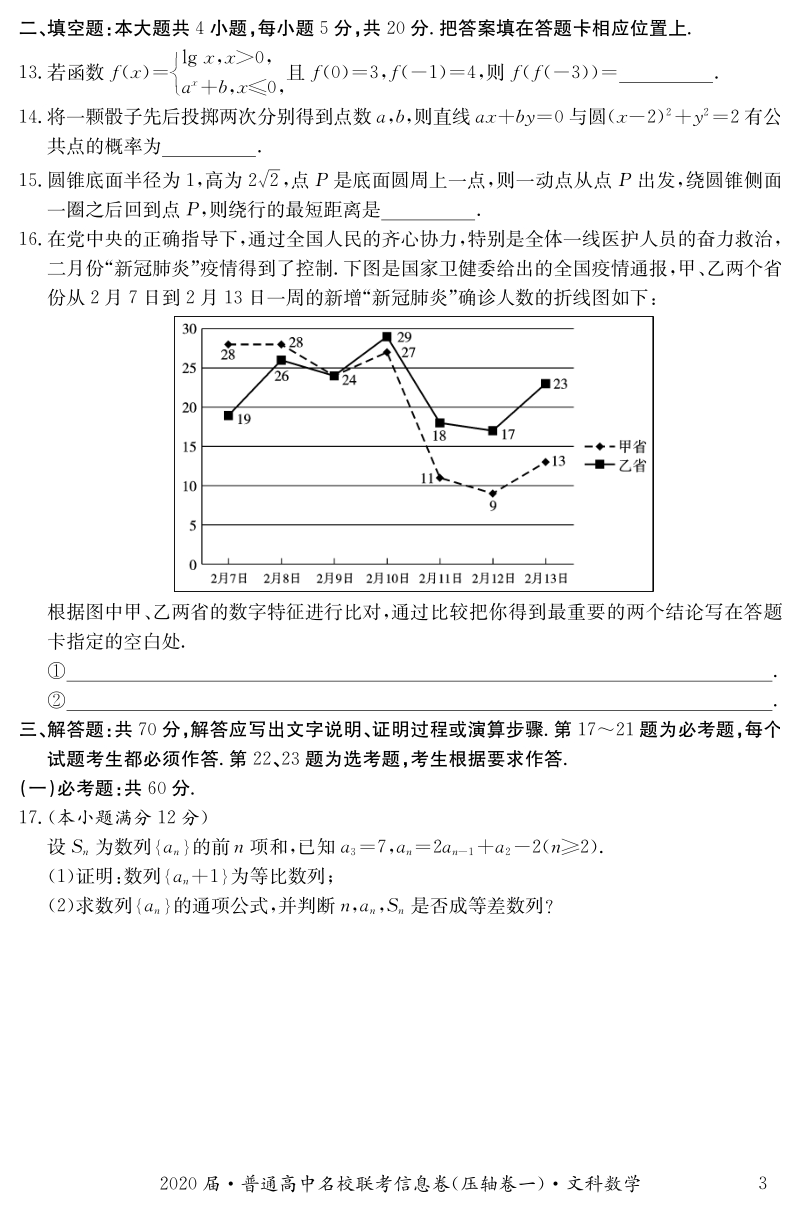
5、圆周上一点， 则一动点从点犘出发， 绕圆锥侧面 一圈之后回到点犘， 则绕行的最短距离是 在党中央的正确指导下， 通过全国人民的齐心协力， 特别是全体一线医护人员的奋力救治， 二月份“ 新冠肺炎” 疫情得到了控制 下图是国家卫健委给出的全国疫情通报， 甲、 乙两个省 份从 月日到月 日一周的新增“ 新冠肺炎” 确诊人数的折线图如下： 根据图中甲、 乙两省的数字特征进行比对， 通过比较把你得到最重要的两个结论写在答题 卡指定的空白处 三、 解答题： 共 分， 解答应写出文字说明、 证明过程或演算步骤第 题为必考题， 每个 试题考生都必须作答 第 、 题为选考题， 考生根据要求作答 （ 一） 必考题
6、： 共 分 （ 本小题满分 分） 设犛 狀为数列犪 狀 的前狀项和， 已知犪 ，犪狀 犪狀 犪 （狀 ） （ ） 证明： 数列犪狀 为等比数列； （ ） 求数列犪 狀 的通项公式， 并判断狀，犪 狀，犛狀是否成等差数列？ 届普通高中名校联考信息卷（ 压轴卷一） 文科数学 （ 本小题满分 分） 由于受到网络电商的冲击， 某品牌的高压锅在线下的销售受到影响， 承受了一定的经济损 失， 现将犃地区 家实体店该品牌高压锅的月经济损失统计如图所示 （ ） 求 犪的值； （ ） 求 犃地区 家实体店该品牌高压锅的月经济损失的众数以及中位数； （ ） 不经过计算， 直接给出犃地区 家实体店经济损失的平均数珚
7、狓与 的大小关系 （ 本小题满分 分） 如图， 在多面体犃 犅 犆 犇 犈 犉中， 底面犃 犅 犆 犇是正方形， 梯形 犃 犇 犈 犉底面犃 犅 犆 犇 ， 且 犃 犉犈 犉犇 犈 犃 犇 （ ） 证明平面犃 犅 犉平面犆 犇 犉； （ ） 平面犆 犇 犉将多面体犃 犅 犆 犇 犈 犉分成两部分， 求两部分的体 积比 届普通高中名校联考信息卷（ 压轴卷一） 文科数学 （ 本小题满分 分） 已知椭圆犆： 狓 犪 狔 犫 （ 犪犫 ） 的短轴长为槡， 离心率为槡 （ ） 求椭圆犆的标准方程； （ ） 直线犾平行于直线狔犫 犪 狓， 且与椭圆犆交于犃，犅两个不同的点， 若?犃 犗 犅为钝角， 求 直
8、线犾在狓轴上的截距犿的取值范围 （ 本小题满分 分） 已知函数犳（狓） 狓犪 狓 （ 犪犚） （ ） 讨论函数犳（狓） 的单调性； （ ） 令 犵（犪） 犪（犽 ） 犪 ， 若对任意的狓 ，犪 ， 恒有犳（狓）犵（犪） 成立， 求实数犽的最 大整数 届普通高中名校联考信息卷（ 压轴卷一） 文科数学 （ 二） 选考题： 共 分 请考生在第 、 题中任选一题作答 如果多做， 则按所做的第一题计 分 （ 本小题满分 分） 选修 ： 坐标系与参数方程 在直角坐标系狓 犗 狔中， 曲线犆的参数方程为 狓 ， 狔 （ 为参数） ， 曲线犆： 狓 狔 （ ） 在以犗为极点，狓轴的正半轴为极轴的极坐标系中，
9、求犆，犆的极坐标方程； （ ） 射线 （ ） 与 犆的异于极点的交点为犃 ， 与 犆的交点为犅 ， 求 犃 犅 （ 本小题满分 分） 选修 ： 不等式选讲 已知函数犳（狓） 狓犪（犪犚） （ ） 当 犪 时， 解不等式狓 犳（狓） ； （ ） 设不等式狓 犳（狓）狓的解集为犕， 若 ， 犕， 求实数犪的取值范围 届普通高中名校联考信息卷（ 压轴卷一） 文科数学 书书书 届普通高中名校联考信息卷（ 压轴卷一） 文科数学 参考答案 题号 答案 槡 甲省比乙省新增人数的平均数低 甲省比乙省的方差要大 解： （） 证明： 因为犪 ，犪 犪 ， 所以犪 ， （ 分） 所以犪 狀 犪狀 ， （ 分） 所以
10、犪 ， （ 分） 犪狀 犪狀 犪狀 犪狀 （ 狀 ） ， （ 分） 所以数列犪 狀 是首项为犪 ， 公比为的等比数列 （ 分） （ ） 由（） 知，犪狀 狀， （ 分） 所以犪 狀 狀 （ 分） 所以犛 狀 （ 狀） 狀 狀 狀 ， （ 分） 所以狀犛 狀 犪狀狀（ 狀 狀 ） （ 狀 ） ， （ 分） 所以狀犛 狀 犪狀 （ 分） 即狀，犪 狀，犛狀成等差数列 （ 分） 解： （ ） 依题意有（ 犪 ） ， 解得犪 （ 分） （ ） 由图可知，犃地区 家实体店该品牌高压锅的月经济损失的众数为 ， 第一块小矩形的面积犛 ， 第二块小矩形的面积犛 ， 故所求中位数在 ， ） 之间， 故所求中位数
11、为 （ 分） （ ） 由频率分布直方图得珚狓 （ 分） 届普通高中名校联考信息卷（ 压轴卷一） 文科数学参考答案 （） 证明： 因为底面犃 犅 犆 犇是正方形， 所以犃 犅犃 犇， 因为梯形犃 犇 犈 犉底面犃 犅 犆 犇， 所以犃 犅平面犃 犇 犈 犉， 因为犇 犉平面犃 犇 犈 犉， 所以犃 犅犇 犉 因为梯形犃 犇 犈 犉中，犃 犉犈 犉犇 犈 犃 犇， 取 犃 犇的中点 犌， 连接犉 犌， 所以犉 犌 犃 犇， 所以犇 犉犃 犉 因为犃 犉犃 犅犃， 所以犇 犉平面犃 犅 犉， 因为犇 犉平面犆 犇 犉， 所以平面犃 犅 犉平面犆 犇 犉（ 分） （ ） 如图， 过 犉作犉犕犃 犇于犕
12、 ， 过 犈作犈 犖犃 犇于犖 ， 作 犕犌犃 犅交犅 犆于犌，犖犎犆 犇交犅 犆于犎 因为梯形犃 犇 犈 犉底面犃 犅 犆 犇 ， 且 犃 犉犈 犉犇 犈 犃 犇 所以犉犕平面犃 犅 犆 犇，犈 犖平面犃 犅 犆 犇 在 犃 犉 犇中， 由犃 犇 犃 犉可得犉 犃 犇 令犃 犉犈 犉犇 犈 犃 犇 ， 则犉犕犈 犖 槡 ，犃犕犖犇 ， 多面体犃 犅 犆 犇 犈 犉的体积犞犞犉 犃 犅 犌 犕犞犈 犆 犇 犖犎犞犉 犕 犌 犈 犖犎 槡 槡 槡 由（ ） 及对称性可得犃 犈平面犆 犇 犈， 因为犃 犇 犈 犉，犈 犉犃 犇， 所以犉到平面犆 犇 犈的距离等于犃到平面犆 犇 犈的距离的一半， 即
13、犉到平面犆 犇 犈的距离等于犱 犃 犈槡 ， 故犞犉 犆 犇 犈 犛犆 犇 犈犱 槡 槡 所以平面犆 犇 犉将多面体犃 犅 犆 犇 犈 犉分成两部分， 两部分的体积比为 （ 分） 解： （ ） 由题意可得犫槡 ， 所以犫槡 ， （ 分） 犲犮 犪 犫 犪槡 槡 ， 解得犪槡 ， （ 分） 所以椭圆犆的标准方程为 狓 狔 （ 分） （ ） 由于直线犾平行于直线狔犫 犪 狓 ， 即 狔 狓， 设直线犾在狔轴上的截距为狀， 届普通高中名校联考信息卷（ 压轴卷一） 文科数学参考答案 所以犾的方程为狔 狓狀（狀 ） （ 分） 由 狔 狓狀， 狓 狔 烅 烄 烆 ， 得狓 狀 狓 狀 ， 因为直线犾与椭圆
14、犆交于犃，犅两个不同的点， 所以（狀） （ 狀 ） ， 解得 狀 （ 分） 设犃（狓， 狔） ，犅（狓，狔） ， 则狓狓 狀，狓狓 狀 犃 犗 犅为钝角等价于 犗 犃 犗 犅 ， 且 狀 ， （ 分） 由 犗 犃 犗 犅狓狓狔狔狓狓（ 狓狀） （ 狓狀） 狓狓狀 （ 狓狓）狀 （ 狀 ） 狀 （ 狀）狀 ， 即狀 ， 且 狀 ， 直线犾在狔轴上的截距狀的取值范围是（槡 ，）（，槡 ） 所以直线犾在狓轴上的截距犿的取值范围是（ 槡 ，）（，槡） （ 分） 解： （） 此函数的定义域为（，） ， 犳 （ 狓） 狓 犪 狓 狓犪 狓 ， 当犪 时， 犳 （ 狓） ， 所以犳（狓） 在（，） 上单调递
15、增； （ 分） 当犪 时， 狓（，犪） ， 犳 （ 狓） ，犳（狓） 单调递减， 狓（犪，） ， 犳 （ 狓） ，犳（狓） 单调递增 综上所述， 当犪 时， 犳（狓） 在（，） 上单调递增； 当犪 时， 犳（狓） 在（，犪） 上单调递减， 在（犪，） 上单调递增 （ 分） （ ） 由（） 知，犳（狓） 犳（犪） 犪 ， 所以犳（狓）犵（犪） 恒成立， 则只需 犪 犵（犪） 恒成立，（ 分） 则 犪 犪（犽 ） 犪 犽 犪， 即 犪 犪 犽 （ 分） 令犺（犪） 犪 犪， 则只需犺 （ 犪） 犽 ， 因为犺 （犪） 犪 犪 犪 犪 ，（ 分） 所以犪（，） 时，犺 （犪） ，犺（犪） 单调递减，
16、 犪（，） 时，犺 （犪） ，犺（犪） 单调递增， 届普通高中名校联考信息卷（ 压轴卷一） 文科数学参考答案 所以犺（犪） 犺（） ， （ 分） 即 犽 ， 所以犽 ， 所以实数犽的最大整数为 （ 分） （） 曲线犆： 狓 ， 狔 烅 烄 烆 （ 为参数） 可化为普通方程为（狓 ） 狔 （ 分） 由 狓 ， 狔 烅 烄 烆 可得曲线犆的极坐标方程为 ， 曲线犆的极坐标方程为 （ ） （ 分） （ ） 射线 （ ） 与曲线犆的交点犃的极径为 槡 ， 射线 （ ） 与曲线犆的交点犅的极径满足 （ ） ， 解得 槡 ， 所以犃 犅 槡 槡 （ 分） 解： （ ） 当 犪 时， 原不等式可化为 狓 狓 （ 分） 当狓 时， 狓 狓 ， 解得狓 ， 所以狓 ； （ 分） 当 狓 时， 狓 狓 ， 解得狓 ， 所以 狓 ； （ 分） 当狓 时， 狓 狓 ， 解得狓 ， 所以狓 （ 分） 综上所述， 当犪 时， 不等式的解集为狓狓 或狓 （ 分） （ ） 不等式狓 犳（狓）狓可化为 狓 狓犪 狓， 依题意不等式 狓 狓犪 狓在狓 ， 上恒成立， （ 分） 所以 狓 狓犪 狓 ， 即 狓犪 ， 即 犪 狓犪 ， （ 分） 所以 犪 ， 犪 烅 烄 烆 ， 解得 犪 ， 故所求实数犪的取值范围是 ， （ 分） 届普通高中名校联考信息卷（ 压轴卷一） 文科数学参考答案
