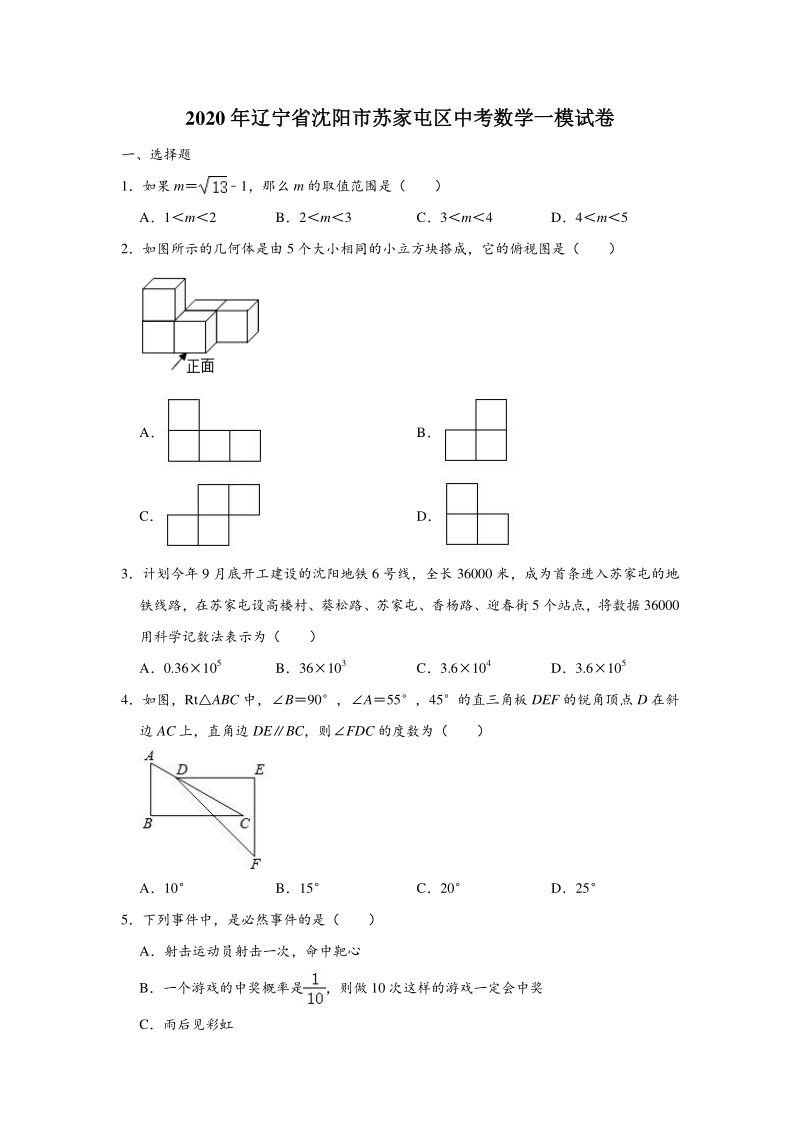
1、2020 年辽宁省沈阳市苏家屯区中考数学一模试卷年辽宁省沈阳市苏家屯区中考数学一模试卷 一、选择题 1如果 m1，那么 m 的取值范围是（ ） A1m2 B2m3 C3m4 D4m5 2如图所示的几何体是由 5 个大小相同的小立方块搭成，它的俯视图是（ ） A B C D 3计划今年 9 月底开工建设的沈阳地铁 6 号线，全长 36000 米，成为首条进入苏家屯的地 铁线路，在苏家屯设高楼村、葵松路、苏家屯、香杨路、迎春街 5 个站点，将数据 36000 用科学记数法表示为（ ） A0.36105 B36103 C3.6104 D3.6105 4如图，RtABC 中，B90，A55，45的直三
2、角板 DEF 的锐角顶点 D 在斜 边 AC 上，直角边 DEBC，则FDC 的度数为（ ） A10 B15 C20 D25 5下列事件中，是必然事件的是（ ） A射击运动员射击一次，命中靶心 B一个游戏的中奖概率是，则做 10 次这样的游戏一定会中奖 C雨后见彩虹 D任意画一个三角形，其外角和是 360 6下列计算正确的是（ ） Aa3+a32a6 Ba4 （a3）2a10 Ca6a2a3 D（ab）2a2b2 7如图，A，B 两景点相距 20km，C 景点位于 A 景点北偏东 60方向上，位于 B 景点北偏 西 30方向上，则 A，C 两景点相距（ ） A10km B10km C10km
3、Dkm 8新型冠状病毒疫情期间，根据某地 2 月 1 日至 5 日这 5 天确诊病例增加数目得到一组数 据：3，5，3，0，7，下列说法正确的是（ ） A众数是 2 B平均数是 3.5 C中位数是 3 D方差是 13 9如图，O 是四边形 ABCD 的外接圆，连接 OB、OD，若四边形 ABOD 是平行四边形， 则ABO 的度数是（ ） A50 B55 C60 D65 10已知二次函数 yax2+bx+c（a0）的图象如图所示，对称轴为直线 x2，与 x 轴的一 个交点（1，0），则下列结论正确的个数是（ ） 当 x1 或 x5 时，y0； a+b+c0； 当 x2 时，y 随 x 的增大而增
4、大； abc0 A3 B2 C1 D0 二.填空题（请将正确答案写在答题卡上，每小题 3 分，共 18 分） 11分解因式：a32a2+a 12关于 x 的一元二次方程（a2）x22x4+a20 有一个根是 0，则 a 的值为 13如图，ABC 与DEF 位似，位似中心为点 O，且 BC：EF3：2，则 SABC：SDEF 14将抛物线 y3（x2）2+1 向左平移 2 个单位，再向下平移 1 个单位，则所得抛物线的 表达式为 15在平面直角坐标系中，点 A 的坐标为（2，1），点 B 的坐标为（2，9），点 C 到直线 AB 的距离为 4，且ABC 是直角三角形，则满足条件的点 C 有 个
5、16如图，正方形 ABCD 中，点 E、F 分别在边 BC、CD 上，连接 AE、EF、AF，且EAF 45，下列结论： ABEADF； AEBAEF； 正方形 ABCD 的周长2CEF 的周长； SABE+SADFSCEF，其中正确的是 （只填写序号） 三、解答题（第 17 题 6 分，第 18、19 小题各 8 分，共 22 分） 17先化简，再求值：，其中 xtan60+（） 2 18 为了庆祝防控新冠肺炎疫情的胜利， 某校举行班级抗击疫情优秀歌曲歌咏比赛， 歌曲有： 逆行英雄，中国一定强，爱的承诺（分别用字母 A，B，C，依次表示这三 首歌曲），比赛时，将 A，B，C，这三个字母分别写
6、在 3 张无差别不透明的卡片正面上， 洗匀后正面向下放在桌面上，九年一班班长先从中随机抽取一张卡片，放回后洗匀，再 由九年二班班长从中随机抽取一张卡片，进行歌咏比赛 （1）九年一班抽中歌曲中国一定强的概率是 ； （2）试用画树状图或列表的方法表示所有可能的结果，并求出九年一班和九年二班抽中 相同歌曲的概率 19如图，四边形 ABCD 中，ADBC，A90，CDCB，过点 C 作DCB 的平分线 CE 交 AB 于点 E，连接 DE，过点 D 作 DFAB，且交 CE 于 F 点，连接 BF （1）求证：四边形 DEBF 是菱形； （2）若 AB5，BC13，求 tanAED 的值 四、（每小题
7、 8 分，共 16 分） 20 为丰富学生的文体生活， 某校计划开设五门选修课程： 声乐、 足球、 舞蹈、 书法、 演讲 要 求每名学生必须选修且只能选修一门课程，为保证计划的有效实施，学校随机对部分学 生进行了一次调查，并将调查结果绘制成如图不完整的统计图请根据统计图解答下列 问题 （1）本次接受问卷调查的学生有 名； （2）补全条形统计图； （3）扇形统计图中选修“演讲”课程所对应扇形的圆心角的度数为 ； （4）该校有 800 名学生，请你估计选修“足球”课程的学生有多少名 21某物业公司计划对所管理的小区 3000m2区域进行绿化，经投标由甲、乙两个工程队来 完成，甲、乙两个工程队每天共
8、完成绿化面积 150m2，甲队完成 600m2区域的绿化面积 与乙队完成 300m2区域的绿化面积所用的天数相同 （1）求甲、乙两个工程队每天各能完成多少面积的绿化？ （2）若甲队每天绿化费用是 0.6 万元，乙队每天绿化费用是 0.2 万元，该物业公司要使 这次绿化总费用不超过 17 万元，则至少安排乙工程队绿化多少天？ 五、（本题 10 分) 22如图，在O 中，AB 为O 的直径，过 O 点作 OCAB 且交O 于 C 点，延长 AB 到 D，过点 D 作O 的切线 DE，切点为 E，连接 CE 交 AB 于 F 点 （1）求证：DEDF； （2）若O 的半径为 2，求 CFCE 的值；
9、 （3）若O 的半径为 2，D30，则阴影部分的面积 六、（本题 10 分） 23如图，过原点的直线 y1mx（m0）与反比例函数 y2（k0）的图象交于 A、B 两点，点 A 在第二象限，且点 A 的横坐标为1，点 D 在 x 轴负半轴上，连接 AD 交反比 例函数图象于另一点 E，AC 为BAD 的平分线，过点 B 作 AC 的垂线，垂足为 C，连接 CE，若 AD2DE，AEC 的面积为 （1）根据图象回答：当 x 取何值时，y1y2； （2）求AOD 的面积； （3）若点 P 的坐标为（m，k），在 y 轴的轴上是否存在一点 M，使得OMP 是直角三 角形，若存在，请直接写出点 M 的
10、坐标；若不存在，请说明理由 七、（本题 12 分） 24已知，把 45的直三角板的直角顶点 E 放在边长为 6 的正方形 ABCD 的一边 BC 上， 直三角板的一条直角边经过点 D， 以 DE 为一边作矩形 DEFG， 且 GF 过点 A， 得到图 1 （1）求矩形 DEFG 的面积； （2）若把正方形 ABCD 沿着对角线 AC 剪掉一半得到等腰直角三角形 ABC，把 45的 直三角板的一个 45角的顶点与等腰直角三角形 ABC 的直角顶点 B 重合， 直三角板夹这 个 45角的两边分别交 CA 和 CA 的延长线于点 H、P，得到图 2猜想：CH、PA、HP 之间的数量关系，并说明理由；
11、 （3）若把边长为 6 的正方形 ABCD 沿着对角线 AC 剪掉一半得到等腰直角三角形 ABC， 点 M 是 RtABC 内一个动点，连接 MA、MB、MC，设 MA+MB+MCy，直接写出 y2 的最小值 八、（本题 12 分） 25 如图， 在平面直角坐标系中， 抛物线 yax2+2x+c 与 y 轴交于点 A， 与 x 轴交于点 B （3， 0）、C（1，0）两点 （1）求直线 AB 和抛物线的表达式； （2）当点 F 为直线 AB 上方抛物线上一动点（不与 A、B 重合），过点 F 作 FPx 轴交 直线 AB 于点 P；过点 F 作 FRy 轴交直线 AB 于点 R，求 PR 的最
12、大值； （3）把射线 BA 绕着点 B 逆时针旋转 90得到射线 BM，点 E 在射线 BM 运动（不与点 B 重合），以 BC、BE 为邻边作平行四边形 BCDE，点 H 为 DE 边上动点，连接 CH，请 直接写出 CH+HE 的最小值 参考答案参考答案 一、选择题（下列各题的四个选项中，只有一个是正确的，请将正确答案涂在答题卡上，每 小题 2 分，共 20 分） 1如果 m1，那么 m 的取值范围是（ ） A1m2 B2m3 C3m4 D4m5 【分析】首先确定的取值范围，然后可得1 的取值范围 解：34， 213， m1， 2m3， 故选：B 2如图所示的几何体是由 5 个大小相同的小
13、立方块搭成，它的俯视图是（ ） A B C D 【分析】找到从上面看所得到的图形即可，注意所有的看到的棱都应表现在俯视图中 解： 从上面看共有 3 列两层， 从左到右第一列底层是一个正方形， 第二列是两个正方形， 第三列上层是一个正方形 故选：C 3计划今年 9 月底开工建设的沈阳地铁 6 号线，全长 36000 米，成为首条进入苏家屯的地 铁线路，在苏家屯设高楼村、葵松路、苏家屯、香杨路、迎春街 5 个站点，将数据 36000 用科学记数法表示为（ ） A0.36105 B36103 C3.6104 D3.6105 【分析】科学记数法的表示形式为 a10n的形式，其中 1|a|10，n 为整
14、数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相 同当原数绝对值10 时，n 是正数；当原数的绝对值1 时，n 是负数 解：360003.6104， 故选：C 4如图，RtABC 中，B90，A55，45的直三角板 DEF 的锐角顶点 D 在斜 边 AC 上，直角边 DEBC，则FDC 的度数为（ ） A10 B15 C20 D25 【分析】根据CDFEDFEDC，求出EDC 即可解决问题 解：B90，A55， C35， DEBC， CEDC35， EDF45， CDFEDFEDC453510， 故选：A 5下列事件中，是必然事件的是（ ） A射
15、击运动员射击一次，命中靶心 B一个游戏的中奖概率是，则做 10 次这样的游戏一定会中奖 C雨后见彩虹 D任意画一个三角形，其外角和是 360 【分析】根据事件发生的可能性大小判断 解：A、射击运动员射击一次，命中靶心是随机事件，不符合题意； B、一个游戏的中奖概率是，则做 10 次这样的游戏不一定会中奖是随机事件，不符合 题意； C、雨后见彩虹是随机事件，不符合题意； D、任意画一个三角形，其外角和是 360是必然事件，符合题意； 故选：D 6下列计算正确的是（ ） Aa3+a32a6 Ba4 （a3）2a10 Ca6a2a3 D（ab）2a2b2 【分析】各项计算得到结果，即可作出判断 解：
16、A、原式2a3，不符合题意； B、原式a4 a6a10，符合题意； C、原式a4，不符合题意； D、原式a22ab+b2，不符合题意 故选：B 7如图，A，B 两景点相距 20km，C 景点位于 A 景点北偏东 60方向上，位于 B 景点北偏 西 30方向上，则 A，C 两景点相距（ ） A10km B10km C10km Dkm 【分析】根据题意可得，CAB30，CBA60，所以ACB90，根据 AB 20km，和特殊角三角函数即可求出 A，C 两景点距离 解：根据题意可知： CAB30，CBA60， ACB60+3090，AB20km， ACABcos302010（km） A，C 两景点相
17、距 10km 故选：B 8新型冠状病毒疫情期间，根据某地 2 月 1 日至 5 日这 5 天确诊病例增加数目得到一组数 据：3，5，3，0，7，下列说法正确的是（ ） A众数是 2 B平均数是 3.5 C中位数是 3 D方差是 13 【分析】将数据重新排列，再根据众数、平均数、中位数及方差的定义求解可得 解：将数据重新排列为 0、3、3、5、7， 则这组数据的众数是 3， 平均数为3.6， 中位数为 3， 方差为 （03.6） 2+2（33.6）2+（53.6）2+（73.6）25.44， 故选：C 9如图，O 是四边形 ABCD 的外接圆，连接 OB、OD，若四边形 ABOD 是平行四边形，
18、 则ABO 的度数是（ ） A50 B55 C60 D65 【分析】由四边形 ABOD 是平行四边形，推出ABOD，由BOD2C，A+ C180，推出C60，ABOD120即可解决问题 解：四边形 ABOD 是平行四边形， ABOD， BOD2C，A+C180， C60，ABOD120， ADOB， ABO+DAB180， ABO60， 故选：C 10已知二次函数 yax2+bx+c（a0）的图象如图所示，对称轴为直线 x2，与 x 轴的一 个交点（1，0），则下列结论正确的个数是（ ） 当 x1 或 x5 时，y0； a+b+c0； 当 x2 时，y 随 x 的增大而增大； abc0 A3
19、B2 C1 D0 【分析】由抛物线的对称轴结合抛物线与 x 轴的一个交点坐标，可求出另一交点坐标， 结进而结合图形分析得出答案 解：根据函数的对称性，抛物线与 x 轴的另外一个交点的坐标为（5，0）， 从图象上看，x1 或 x5 时，y0，故正确，符合题意； 从图象看，当 x1 时，ya+b+c0，故错误，不符合题意； 从图象看 x2 时，y 随 x 的增大而增大，故正确，符合题意； 从图象看，a0，b0，c0，故 abc0，故正确，符合题意； 故选：A 二.填空题（请将正确答案写在答题卡上，每小题 3 分，共 18 分） 11分解因式：a32a2+a a（a1）2 【分析】此多项式有公因式，
20、应先提取公因式 a，再对余下的多项式进行观察，有 3 项， 可利用完全平方公式继续分解 解：a32a2+a a（a22a+1） a（a1）2 故答案为：a（a1）2 12关于 x 的一元二次方程（a2）x22x4+a20 有一个根是 0，则 a 的值为 2 【分析】把 x0 代入方程（a2）x22x4+a20 得4+a20，再解关于 a 的方程， 然后利用一元二次方程的定义得到 a20，从而确定 a 的值 解：把 x0 代入方程（a2）x22x4+a20 得4+a20，解得 a2 或 a2， 因为 a20， 所以 a 的值为2 故答案为2 13如图，ABC 与DEF 位似，位似中心为点 O，且
21、 BC：EF3：2，则 SABC：SDEF 9：4 【分析】根据位似图形的概念得到ABCDEF，根据相似三角形的性质计算即可 解：ABC 与DEF 位似， ABCDEF， BC：EF3：2， （）2， 故答案为：9：4 14将抛物线 y3（x2）2+1 向左平移 2 个单位，再向下平移 1 个单位，则所得抛物线的 表达式为 y3x2 【分析】直接利用抛物线平移规律：上加下减，左加右减进而得出平移后的解析式 解：将抛物线 y3（x2）2+1 向左平移 2 个单位，再向下平移 1 个单位， 平移后的抛物线的解析式为：y3（x2+2）2+11，即 y3x2 故答案为 y3x2 15在平面直角坐标系中
22、，点 A 的坐标为（2，1），点 B 的坐标为（2，9），点 C 到直线 AB 的距离为 4，且ABC 是直角三角形，则满足条件的点 C 有 6 个 【分析】 当A90时， 满足条件的 C 点 2 个； 当B90时， 满足条件的 C 点 2 个； 当C90时，满足条件的 C 点 2 个所以共有 6 个 解：点 A，B 的横坐标坐标相等， ABy 轴， 点 C 到直线 AB 的距离为 4， 点 C 在平行于 AB 的两条直线上 过点 A 的垂线与那两条直线有 2 个交点，过点 B 的垂线与那两条直线有 2 个交点，以 AB 为直径的圆与那两条直线有 2 个交点 满足条件的 C 点共 6 个 故答
23、案为：6 16如图，正方形 ABCD 中，点 E、F 分别在边 BC、CD 上，连接 AE、EF、AF，且EAF 45，下列结论： ABEADF； AEBAEF； 正方形 ABCD 的周长2CEF 的周长； SABE+SADFSCEF，其中正确的是 （只填写序号） 【分析】E、F 不分别是 BC 和 CD 的中点时，BEDF，则ABE 和ADF 的三边全 部对应相等，由此得出判断； 延长 CD 至 G，使得 DGBE，证明ABEADG 和AEFAGF，便可判断正 误； 通过周长公式计算，再由 BE+DFEF，得出判断； 证明 SABE+SADFSAGF， 再由三角形的底与高的数量关系得 SAG
24、FSCEF， 进而得出 判断 解：当 E、F 不分别是 BC 和 CD 的中点时，BEDF，则ABEADF 不成立，故 错误； 延长 CD 至 G，使得 DGBE，如图 1， ABAD，ABEADG90， ABEADG（SAS）， BAEDAG，AEBG，AEAG， BAD90，EAF45， BAE+DAF45， GAFDAG+DAF45， EAFFAG， AFAF， AEFAGF（SAS）， AEFG， AEBAEF， 故正确； AEFAGF， EFGFDG+DFBE+DF， CEF 的周长CE+CF+EFCE+CF+BE+DFBC+CD2BC， 正方形 ABCD 的周长4BC， 正方形 A
25、BCD 的周长2CEF 的周长， 故正确； ABEADG， SABESADG， SABE+SADFSAGF， GFEFCF，ADCE， ，即 SAGFSCEF， SABE+SADFSCEF， 故错误； 故答案为： 三、解答题（第 17 题 6 分，第 18、19 小题各 8 分，共 22 分） 17先化简，再求值：，其中 xtan60+（） 2 【分析】先把除法变成乘法，算乘法，算减法，最后代入求出即可 解： ， 当 xtan60+（） 2 +4 时，原式 18 为了庆祝防控新冠肺炎疫情的胜利， 某校举行班级抗击疫情优秀歌曲歌咏比赛， 歌曲有： 逆行英雄，中国一定强，爱的承诺（分别用字母 A，
26、B，C，依次表示这三 首歌曲），比赛时，将 A，B，C，这三个字母分别写在 3 张无差别不透明的卡片正面上， 洗匀后正面向下放在桌面上，九年一班班长先从中随机抽取一张卡片，放回后洗匀，再 由九年二班班长从中随机抽取一张卡片，进行歌咏比赛 （1）九年一班抽中歌曲中国一定强的概率是 ； （2）试用画树状图或列表的方法表示所有可能的结果，并求出九年一班和九年二班抽中 相同歌曲的概率 【分析】（1）直接根据概率公式计算可得； （2）画树状图得出所有等可能结果，再从中找到符合条件的结果数，利用概率公式计算 可得 解：（1）因为有 A，B，C3 种等可能结果， 所以九年一班抽中歌曲中国一定强的概率； 故答
27、案为：； （2）画树状图如图所示： 共有 9 种可能，其中九年一班和九年二班抽中相同歌曲有 3 种（A，A）， （B，B）， （C， C）， 九年一班和九年二班抽中相同歌曲的概率 19如图，四边形 ABCD 中，ADBC，A90，CDCB，过点 C 作DCB 的平分线 CE 交 AB 于点 E，连接 DE，过点 D 作 DFAB，且交 CE 于 F 点，连接 BF （1）求证：四边形 DEBF 是菱形； （2）若 AB5，BC13，求 tanAED 的值 【分析】（1）证明CDECBE，根据全等三角形的性质得到 EDEB，DEC BEC，根据平行线的性质、等腰三角形的判定定理得到 DEDF，根
28、据菱形的判定定理 证明； （2）根据矩形的性质得到BGD90，DGAB5，ADBG，根据勾股定理求出 GC，求出 AD，根据勾股定理列方程求出 AE，根据正切的定义计算，得到答案 【解答】（1）证明：CE 平分DCB， DCEBCE， 在CDE 和CBE 中， ， CDECBE（SAS）， EDEB，DECBEC， DFAB， DFEBEC， DFEDEC， DEDF， DFBE，又 DFAB，DEDF， 四边形 DEBF 为菱形； （2）解：ADBC，ABDF， 四边形 ABGD 为平行四边形， A90， 四边形 ABGD 为矩形， BGD90，DGAB5，ADBG， 在 RtDGC 中，G
29、C12， ADBGBCGC13121， 设 AEx，则 DEBE5x， 在 RtADE 中，DE2AE2+AD2，即（5x）2x2+12， 解得，x， tanAED 四、（每小题 8 分，共 16 分） 20 为丰富学生的文体生活， 某校计划开设五门选修课程： 声乐、 足球、 舞蹈、 书法、 演讲 要 求每名学生必须选修且只能选修一门课程，为保证计划的有效实施，学校随机对部分学 生进行了一次调查，并将调查结果绘制成如图不完整的统计图请根据统计图解答下列 问题 （1）本次接受问卷调查的学生有 100 名； （2）补全条形统计图； （3）扇形统计图中选修“演讲”课程所对应扇形的圆心角的度数为 18
30、 ； （4）该校有 800 名学生，请你估计选修“足球”课程的学生有多少名 【分析】（1）根据舞蹈的人数和所占的百分比即可求出本次接受问卷调查的学生数； （2）用总人数减去其它课程的人数，求出喜欢书法的人数，从而补全统计图； （3）用 360乘以选修“演讲”的人数所占的百分比即可； （4）用该校的总人数乘以选修“足球”人数所占的百分比即可得出答案 解：（1）本次接受问卷调查的学生有：3535%100（名）； 故答案为：100； （2）喜欢书法的人数有：10092135530（人）， 补全统计图如下： （3） 扇形统计图中选修 “演讲” 课程所对应扇形的圆心角的度数为： 36018； 故答案为：
31、18； （4）根据题意得： 800168（名）， 答：估计选修“足球”课程的学生有 168 名 21某物业公司计划对所管理的小区 3000m2区域进行绿化，经投标由甲、乙两个工程队来 完成，甲、乙两个工程队每天共完成绿化面积 150m2，甲队完成 600m2区域的绿化面积 与乙队完成 300m2区域的绿化面积所用的天数相同 （1）求甲、乙两个工程队每天各能完成多少面积的绿化？ （2）若甲队每天绿化费用是 0.6 万元，乙队每天绿化费用是 0.2 万元，该物业公司要使 这次绿化总费用不超过 17 万元，则至少安排乙工程队绿化多少天？ 【分析】（1）根据题意结合甲队完成 600m2与乙队完成 30
32、0m2区域的绿化面积所用的天 数相同，得出等式即可； （2）根据要使这次绿化总费用不超过 17 万元，得出不等式进而求出答案 解：（1）设乙工程队每天能完成 xm2的绿化的面积，则甲工程队每天能完成（150x） m2的绿化的面积， 根据题意可得：， 解得：x50， 经检验得：x50 是所列方程的解， 150x15050100， 答： 乙工程队每天能完成50m2的绿化的面积， 甲工程队每天能完成100m2的绿化的面积； （2）设安排乙工程队绿化 y 天， 根据题意可得：0.6+0.2y17， 解得：y10， 答：至少安排乙工程队绿化 10 天 五、（本题 10 分) 22如图，在O 中，AB 为
33、O 的直径，过 O 点作 OCAB 且交O 于 C 点，延长 AB 到 D，过点 D 作O 的切线 DE，切点为 E，连接 CE 交 AB 于 F 点 （1）求证：DEDF； （2）若O 的半径为 2，求 CFCE 的值； （3）若O 的半径为 2，D30，则阴影部分的面积 2 【分析】（1）欲证明 DEDF，只要证明DEFEFD 即可 （2）延长 CO 交O 于 H，连接 EH证明COFCEH，推出，可得 CE CFCO CH 解决问题 （3）根据 S阴SEDOS扇形OEB，只要求出 DE，EOB 即可解决问题 【解答】（1）证明：连接 OE DE 是O 的切线， DEOE， OED90，
34、DEF+OEC90， OCAB， COB90， C+OFC90， OEOC， OECC， OFCDFE， DEFEFD， DEDF （2）解：延长 CO 交O 于 H，连接 EH CH 为直径， CEH90， OCAB， COF90， COFCEH， CC， COFCEH， ， CE CFCO CH248 （3）解：OED90，D30，OE3， OD2OE4，EOB60，DE2， S阴SEDOS 扇形OEB OE DE222 故答案为 2 六、（本题 10 分） 23如图，过原点的直线 y1mx（m0）与反比例函数 y2（k0）的图象交于 A、B 两点，点 A 在第二象限，且点 A 的横坐标为
35、1，点 D 在 x 轴负半轴上，连接 AD 交反比 例函数图象于另一点 E，AC 为BAD 的平分线，过点 B 作 AC 的垂线，垂足为 C，连接 CE，若 AD2DE，AEC 的面积为 （1）根据图象回答：当 x 取何值时，y1y2； （2）求AOD 的面积； （3）若点 P 的坐标为（m，k），在 y 轴的轴上是否存在一点 M，使得OMP 是直角三 角形，若存在，请直接写出点 M 的坐标；若不存在，请说明理由 【分析】（1）根据题意得到点 A，点 B 关于原点对称，求得点 B 的横坐标为 1，于是得 到当 x 取1x0 或 x1 时，y1y2； （2）连接 OC，OE，求得 OAOB，得到
36、OACOCA，根据角平分线的定义得到 OACDAC，推出 ADOC，求得 SAEOSACE，于是得到结论； （3）作 EFx 轴于 F，作 AHx 轴于 H，则 EFAH，求得 DFFH，根据三角形中位 线定理得到 EFAH，求得 y，得到 A（1，2），于是得到 P（2，2）， 根据直角三角形的性质即可得到结论 解：（1）直线 y1mx（m0）与反比例函数 y2（k0）的图象交于 A、B 两点， 且点 A 的横坐标为1， 点 A，点 B 关于原点对称， 点 B 的横坐标为 1， 当 x 取1x0 或 x1 时，y1y2； （2）连接 OC，OE， 由图象知，点 A，点 B 关于原点对称， O
37、AOB， ACCB， ACB90， OCABAO， OACOCA， AC 为BAD 的平分线， OACDAC， OCADAC， ADOC， SAEOSACE ， AD2DE， AEDE， SAOD2SAOE3； （3）作 EFx 轴于 F，作 AHx 轴于 H， 则 EFAH， AD2DE， DEEA， EFAH， 1， DFFH， EF 是DHA 的中位线， EFAH， SOEFSOAH ， OF EFOH HA， OHOF， OHHF， DFFHHODO， SOAHSADO 31， 1， k2， y， 点 A 在 y的图象上， 把 x1 代入得，y2， A（1，2）， 点 A 在直线 ym
38、x 上， m2， P（2，2）， 在 y 轴上找到一点 M，使得OMP 是直角三角形， 当OMP90时，PMy 轴， 则 OM2， 点 M 的坐标为（02）； 当OPM90时，过 P 作 PGy 轴于 G，则OPM 是等腰直角三角形， OM2PG4， 点 M 的坐标为（04）； 综上所述，点 M 的坐标为（02）或（0，4） 七、（本题 12 分） 24已知，把 45的直三角板的直角顶点 E 放在边长为 6 的正方形 ABCD 的一边 BC 上， 直三角板的一条直角边经过点 D， 以 DE 为一边作矩形 DEFG， 且 GF 过点 A， 得到图 1 （1）求矩形 DEFG 的面积； （2）若把
39、正方形 ABCD 沿着对角线 AC 剪掉一半得到等腰直角三角形 ABC，把 45的 直三角板的一个 45角的顶点与等腰直角三角形 ABC 的直角顶点 B 重合， 直三角板夹这 个 45角的两边分别交 CA 和 CA 的延长线于点 H、P，得到图 2猜想：CH、PA、HP 之间的数量关系，并说明理由； （3）若把边长为 6 的正方形 ABCD 沿着对角线 AC 剪掉一半得到等腰直角三角形 ABC， 点 M 是 RtABC 内一个动点，连接 MA、MB、MC，设 MA+MB+MCy，直接写出 y2 的最小值 【分析】 （1） 根据正方形的性质得到ADCDCE90， 根据矩形的性质得到AGD GDE
40、90，根据相似三角形的性质和矩形的面积公式即可得到结论； （2）根据旋转的性质得到 BKBP，PBAKBC，BCKBAP18045 135，由勾股定理得到 CH2+PA2KH2，求得PBA+ABE45，等量代换得到 KBC+ABE45， 根据全等三角形的性质得到HKHP， 根据勾股定理即可得到结论； （3）根据旋转的性质得到 MCKN，BMBK，根据等边三角形的性质得到 MKBM， 于是得到 MA+MB+MCAM+MK+KN，当 A，M，K，N 四点共线时，AN 就是所求的 MA+MB+MC的最小值， 过N作NQAB交AB的延长线于Q， 求得AQAB+BQ6+3， 根据勾股定理即可得到结论 解
41、：（1）四边形 ABCD 是正方形， ADCDCE90， 四边形 DEFG 是矩形， AGDGDE90， DCEAGD90，ADCGDE90， ADCADEGDEADE， EDCADG， EDCADG，DCEAGD90， ECDAGD， ， DG DEDC DA6636， 矩形 DEFG 的面积DG DE36； （2）CH2+PA2HP2， 证明：把BAP 绕着点 B 顺时针旋转 90得到BCK，连接 KH， 由旋转得BAPBCK， BKBP，PBAKBC，BCKBAP18045135， HCKBCKBCA1354590， 由勾股定理得，CH2+PA2KH2， PBE45， PBA+ABE45
42、， PBAKBC， KBC+ABE45， ABC90， HBK45， PBE45， HBKPBE45， BKBP，HBKPBE，BHBH， BHPBHK（SAS）， HKHP， CH2+PA2HK2， CH2+PA2HP2； （3）把BMC 绕着点 B 顺时针旋转 60得到BKN，连接 MK，BN，NC， 由旋转得，BMCBKN， MCKN，BMBK， BMBK，MBK60， BKM 是等边三角形， MKBM， MA+MB+MCAM+MK+KN， 当 A，M，K，N 四点共线时，AN 就是所求的 MA+MB+MC 的最小值， 过 N 作 NQAB 交 AB 的延长线于 Q， NBQ180906
43、030，BQN90， QNBN sin3063，BQBN cos3063， AQAB+BQ6+3， 在 RtAQN 中，由勾股定理得，AN2AQ2+QN2（6+3）2+3272+36， y2的最小值为 72+36 八、（本题 12 分） 25 如图， 在平面直角坐标系中， 抛物线 yax2+2x+c 与 y 轴交于点 A， 与 x 轴交于点 B （3， 0）、C（1，0）两点 （1）求直线 AB 和抛物线的表达式； （2）当点 F 为直线 AB 上方抛物线上一动点（不与 A、B 重合），过点 F 作 FPx 轴交 直线 AB 于点 P；过点 F 作 FRy 轴交直线 AB 于点 R，求 PR
44、的最大值； （3）把射线 BA 绕着点 B 逆时针旋转 90得到射线 BM，点 E 在射线 BM 运动（不与点 B 重合），以 BC、BE 为邻边作平行四边形 BCDE，点 H 为 DE 边上动点，连接 CH，请 直接写出 CH+HE 的最小值 【分析】（1）将点 B，C 坐标代入抛物线解析式中，即可求出 a，c，进而求出点 A 的坐 标，再用待定系数法求出直线 AB 的解析式； （2）先判断出OBAOAB45，进而判断出FPRFRP45，得出PFR 90， PFFR， 进而得出 PRFR， 再设点 R （t， t+3） ， 得出点 F （t， t2+2t+3） ， 进而得出 PRFR（t）2+，即可得出结论； （3）先判断出DEGCBE45，进而判断出 HGHE，即可得出结论 解：（1）抛物线 yax2+2x+c 经过点 B（3，0）、C（1，0）， ， ，
