1、九年级数学测试题九年级数学测试题（2020.05） 第卷第卷（选择选择题题 共共36 分分） 一、选择题一、选择题（本大题共本大题共 12 小题小题，在每个小题给出的四个选项中在每个小题给出的四个选项中，只有一项是正确的只有一项是正确的，请把正请把正 确的选项选出来确的选项选出来，每小题选对得每小题选对得 3 分分，错选、不选或选出的答案超过一个均记错选、不选或选出的答案超过一个均记 0 分分.） 1.下列图形中，既是轴对称图形，又是中心对称图形的是（ ） A. B. C. D. 2.下列各式计算正确的是（ ） A. 339 236xxx B. 4222 ()()ababa b C. 222
2、347xxx D. 222 ()abab 3.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划， “一带一路”地区覆盖总人 口约为 4 800 000 000，将 4 800 000 000 用科学记数法表示为（ ） A. 8 48 10 B. 9 4.8 10 C. 8 4.8 10 D. 10 4.8 10 4.某学校组织学生进行社会主义核心价值观的知识竞赛，进入决赛的共有 20 名学生，他们的决赛成绩如下 表所示： 决赛成绩/分 95 90 85 80 人数 4 6 8 2 那么 20 名学生决赛成绩的平均数和中位数分别是（ ） A.88，87.5 B.87.5，87.
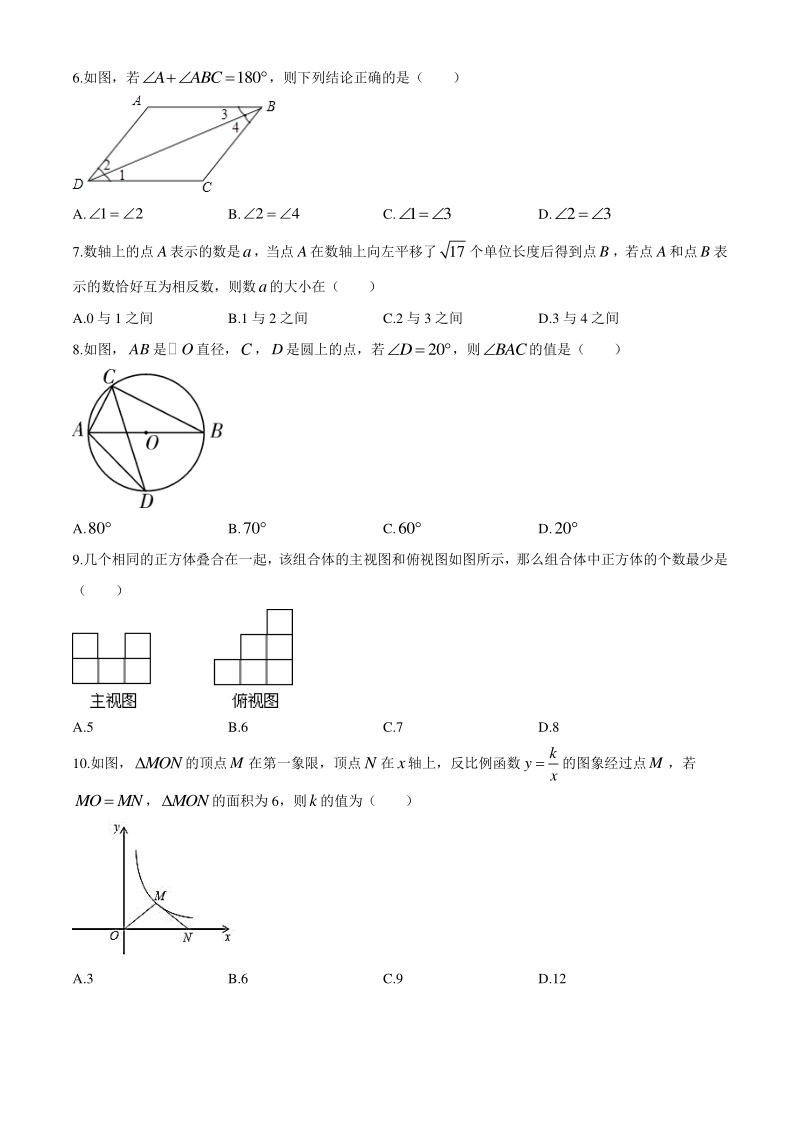
3、5 C.88，90 D.87.5，85 5.如图，在地面上的点A处测得树顶B的仰角75，若6AC 米，则树高BC为（ ） A.6sin75米 B.6cos75米 C. 6 tan75 米 D.6tan75米 6.如图，若180AABC ，则下列结论正确的是（ ） A.12 B.24 C.13 D.23 7.数轴上的点A表示的数是a，当点A在数轴上向左平移了17个单位长度后得到点B，若点A和点B表 示的数恰好互为相反数，则数a的大小在（ ） A.0 与 1 之间 B.1 与 2 之间 C.2 与 3 之间 D.3 与 4 之间 8.如图，AB是O直径，C，D是圆上的点，若20D，则BAC的值是（
4、 ） A.80 B.70 C.60 D.20 9.几个相同的正方体叠合在一起，该组合体的主视图和俯视图如图所示，那么组合体中正方体的个数最少是 （ ） A.5 B.6 C.7 D.8 10.如图，MON的顶点M在第一象限，顶点N在x轴上，反比例函数 k y x 的图象经过点M，若 MOMN，MON的面积为 6，则k的值为（ ） A.3 B.6 C.9 D.12 11.关于x的不等式组 321 2 xx xa ，有四个整数解，则a的取值范围是（ ） A.43a B.32a C.21a D.10a 12.如图，四边形ABCD是正方形，8AB，AC、BD交于点O，点P、Q分别是AB、BD上的动点，
5、点P的运动路径是ABC， 点Q的运动路径是BD， 两点的运动速度相同并且同时结束.若点P的 行程为x，PBQ的面积为y，则y关于x的函数图象大致为（ ） A. B. C. D. 第卷第卷（非选择非选择题题 共共84 分分） 二、填空题二、填空题（本大题共本大题共 6 小题小题，共共 18 分分.只要求填写最后结果只要求填写最后结果，每小题填对得每小题填对得 3 分分.） 13.如图，点D、E分别在线段AB、AC上，且ADAE，若由SAS判定ABEACD，则需要添加 的一个条件是_. 14.分解因式： 32 43m nm nmn_. 15.函数 2 21 4 x y x 的自变量x的取值范围是_
6、. 16.如图，EF是一面足够长的墙，用总长为 30 米的木栅栏（图中的虚线）围一个矩形场地ABCD，中间 用栅栏隔成同样三块.若要围成的矩形面积为 60 平方米，设垂直于墙的边长为x则可列方程为_. 17.如图， 在平面直角坐标系中， 点A、B的坐标分别为(1,4)和(3,0)， 点C是y轴上的一个动点， 连接AC、 BC，当ABC的周长最小值时，ABC的面积为_. 18.如图，在直角坐标系中，抛物线 2 48 4 279 yxx与x轴交于点A、B，与y轴交于点C，点D的坐 标为( 3,0).C的半径为 2，E是C上的一动点，点F是AE的中点，则DF最小值为_. 三、解答题三、解答题（共共
7、7 小题小题；满分满分 66 分分） 19.已知关于x的一元二次方程： 2 (6)50xkxk （1）求证：无论k为何值，方程总有实数根； （2）如果方程的两个实数根为 1 x， 2 x，且 1212 21x xxx，求k的取值范围. 20.2020 年春的新冠肺炎疫情暴发，造成很多不便，为了提高学生对病毒的认知，某校在学生中做了一次抽 样调查，调查结果共分为四个等级：A.非常了解；B.比较了解；C.基本了解；D.不了解，根据调查统计 结果，绘制了不完整的三种统计图表. 对病毒的了解程度的统计表： 对病毒的了解程度 百分比 A.非常了解 5% B.比较了解 m C.基本了解 45% D.不了解
8、 n 请结合统计图表，回答下列问题. （1）本次参与调查的学生共有_人，m_，n_； （2）图 2 所示的扇形统计图中D部分扇形所对应的圆心角是_度； （3）请补全图 1 示数的条形统计图； （4）根据调查结果，学校准备开展关于病毒知识竞赛，某班要从“非常了解”态度的小明和小刚中选一人 参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球标上数字 1，2，3，4，然后放到 一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球.若摸出 的两个球上的数字和为奇数，则小明去；否则小刚去.请用树状图或列表法说明这个游戏规则是否公平. 21.如图，在大楼AB
9、的正前方有一斜坡CD，13CD米，坡比:5:12DE EC ，高为DE，在斜坡下的 点C处测得楼顶B的仰角为58，在斜坡上的点D处测得楼顶B的仰角为31，其中A、C、E在同一 直线上. （1）求斜坡CD的高度DE； （2）求大楼AB的高度； （参考数据sin580.84，cos580.53，tan581.6，sin310.52，cos310.86， tan310.60.） 22.已知，点P为O外一点，直线PA交O于A、B两点，PC切O于点C，ODAB于点H，交 O于D，连接CD交PB于点E. （1）如图 1，求证：PCPE； （2）如图 2，连接BC、BD，点F为CD上一点，且DFBD.求证：
10、BF平分CBP； 23.某农业种植基地种植和销售一种水果，已知该水果的成本是 12 元/千克，规定销售价格不低于成本，又 不高于成本的两倍.经过市场调查发现，某天该水果的销售量y（千克）与销售价格x（元/千克）的函数关 系如下图所示： （1）求y与x之间的函数解析式； （2）求这一天销售这种水果获得的利润W的最大值； （3）若该公司按每销售一千克提取 1 元用于捐资助学，且保证每天的销售利润不低于 3600 元，问该种销 售价格该如何确定. 24.在ABC中，ABAC，90BAC，点D在射线BC上（不与点B、点C重合） ，将线段AD绕A 逆时针旋转90得到线段AE，作射线BA与射线CE，两射线
11、交于点F. （1）若点D在线段BC上，如图 1，请直接写出CD与EF的关系. （2）若点D在线段BC的延长线上，如图 2， （1）中的结论还成立吗？请说明理由. （3）在（2）的条件下，连接DE，G为DE的中点，连接GF，若 1 tan 2 AEC，2AB ，求GF 的长. 25.如图，抛物线 2 4 3 yxbxc 过点(3,0)A，(0,2)B，( ,0)M m为线段OA上一个动点 （点M与点A 不重合） ，过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N. （1）求直线AB的解析式和抛物线的解析式； （2）如果点P是MN的中点，那么求此时点N的坐标； （3）如果以B，P，N为顶
12、点的三角形与APM相似，求点M的坐标. 九年级数学测试题九年级数学测试题（2020.05）答案答案 第卷第卷（选择选择题题 共共36 分分） 一、选择题一、选择题（本大题共本大题共 12 小题小题，在每个小题给出的四个选项中在每个小题给出的四个选项中，只有一项是正确的只有一项是正确的，请把正请把正 确的选项选出来确的选项选出来，每小题选对得每小题选对得 3 分分，错选、不选或选出的答案超过一个均记错选、不选或选出的答案超过一个均记 0 分分.） ACBAD CCBDB AC 第卷第卷（非选择非选择题题 共共84 分分） 二、填空题二、填空题（本大题共本大题共 6 小题小题，共共 18 分分.只
13、要求填写最后结果只要求填写最后结果，每小题填对得每小题填对得 3 分分.） 13.ABAC或BDCE 14.(3)(1)mn mm 15. 1 2 x 且2x 16.(304 )60xx 17.3 18. 3 2 三、解答题三、解答题（共共 7 小题小题；满分满分 66 分分） 19.解： （1）证明： 2 (6)4(5)kk 2 816kk 2 (4)k， 2 (4)0k ， 即0 ， 无论k取何值，该方程总有实数根； （2）解：根据题意得 12 6xxk， 12 5x xk 1212 21x xxx 2(5)61kk 解得5k . 20.解： （1）利用条形图和扇形图可得出：本次参与调查的
14、学生共有：180 45%400； 60 100%15% 400 m ，1 5% 15% 45%35%n ； （2）图 2 所示的扇形统计图中D部分扇形所对应的圆心角是：36035% 126； （3）D等级的人数为：400 35% 140； 如图所示： ； （4）列树状图得： 所以从树状图可以看出所有可能的结果有 12 种，数字之和为奇数的有 8 种， 则小明参加的概率为： 82 123 P ， 小刚参加的概率为： 41 123 P ， 故游戏规则不公平. 21.解： （1）在大楼AB的正前方有一斜坡CD，13CD米，坡度为5:12， 5 12 DE EC ， 设5DEx米，则12ECx米， 2
15、22 (5 )(12 )13xx， 解得，1x ， 55x ，1212x， 即5DE 米，12EC 米， 故斜坡CD的高度DE是 5 米； （2）tan58 AB AC ，tan31 ABDE ECAC ，5DE 米，12CE 米， 1.6 AB AC ， 5 0.6 12 AB AC ， 解得，19.52AB米， 即大楼AB的高度是 19.52 米. 22.（1）证明：如图 1，连接OC， PC切O于C， 90PCDOCD， ODAB， 90DHEDDCEP ， OCOD， OCDD， PCDCEP， PCPE； （2）如图 2， ODAB， ADBD， BCDABD， DFBD， DFBD
16、BF ， DCBCBFFBPABD， CBFPBF， BF平分CBP； 23.解： （1）当1220x时，设ykxb.代(12,2000)，(20,400)， 图图1 O EPH D C B A 图图 2 EA B C D H P F O 得 200012 40020 kb kb 解得 200 4400 k b 2004400yx 当2024x时，400y . 综上， 2004400(1220) 400(2024) xx y x （2）当1220x时， (12)Wxy (12)( 2004400)xx 2 200(17)5000x 当17x 时，W的最大值为 5000； 当2024x时， (1
17、2)Wxy 4004800x. 当24x时，W的最大值为 4800. 最大利润为 5000 元. （3）当1220x时， (12 1)Wxy (13)( 20004400)xx 2 200(17.5)4050x 令 2 200(17.5)40503600x 1 16x ， 2 19x 定价为1619x 当2024x时， 400(13)40052003600Wxx 2224x. 综上，销售价格确定为1619x或2224x. 24.解： （1）CDEF，CDEF， 理由如下：ABAC，90BAC， 45ABCACB， 将线段AD绕A逆时针旋转90得到线段AE， ADAE，90DAEBAC， BAD
18、CAE，且ABAC，ADAE， ABDACE SAS BDCE，45ABDACE， 90BCFACBACE， CDEF， 又45ABC， BFCABC， BCCF， CDEF； （2）结论仍然成立， 理由如下：ABAC，90BAC， 45ABCACB， 将线段AD绕A逆时针旋转90得到线段AE， ADAE，90DAEBAC， BADCAE，且ABAC，ADAE， ABDACE SAS BDCE，45ABDACE， 90BCFACBACE， CDEF， 又45ABC， BFCABC， BCCF， CDEF； （3）如图，过点A作ANCE于点N，过点G作GHCE于H， 2ABAC， 2BCCF，
19、ANCE，45ACF， 1ANCN， 1 tan 2 AN AEC EN ， 2EN ， 3ECCNEN， 1EFECCFCD ， GHCE，90ECD， /HG CD， EGHGEH EDCDEC ，且EGDG， 1 2 HG ， 3 2 EH ， 1 2 FHEHEF 22 112 442 GFHGFH 25.解： （1）设直线AB的解析式为ypxq， 把(3,0)A，(0,2)B代入得 30 2 pq q ，解得 2 3 2 p q ， 直线AB的解析式为 2 2 3 yx ； 把(3,0)A，(0,2)B代入 2 4 3 yxbxc 得 2 4 330 3 2 bc c ，解得 10
20、3 2 b c ， 抛物线解析式为 2 410 2 33 yxx ； （2）( ,0)M m，MNx轴， 2 410 ,2 33 N mmm ， 2 ,2 3 P mm ， 2 4 4 3 NPmm ， 2 2 3 PMm ， 而NPPM， 2 42 42 33 mmm ，解得 1 3m （舍去） ， 2 1 2 m ， N点坐标为 1 10 , 23 ； （3）(3,0)A，(0,2)B， 2 ,2 3 P mm ， 22 3213AB， 2 2 213 22 33 BPmmm ， 而 2 4 4 3 NPmm ， /MN OB， BPNABO， 当 PBPN OBBA 时，BPNOBA，则BPNMPA，即 2 134 :24: 13 33 mmm ， 整理得 2 8110mm，解得 1 0m （舍去） ， 2 11 8 m ， 此时M点的坐标为 11,0 8 ； 当 PBPN BAOB 时，BPNABO，则BPNAPM，即 2 134 : 134:2 33 mmm ， 整理得 2 250mm，解得 1 0m （舍去） ， 2 5 2 m ， 此时M点的坐标为 5 ,0 2 ； 综上所述，点M的坐标为 11,0 8 或 5 ,0 2 .
