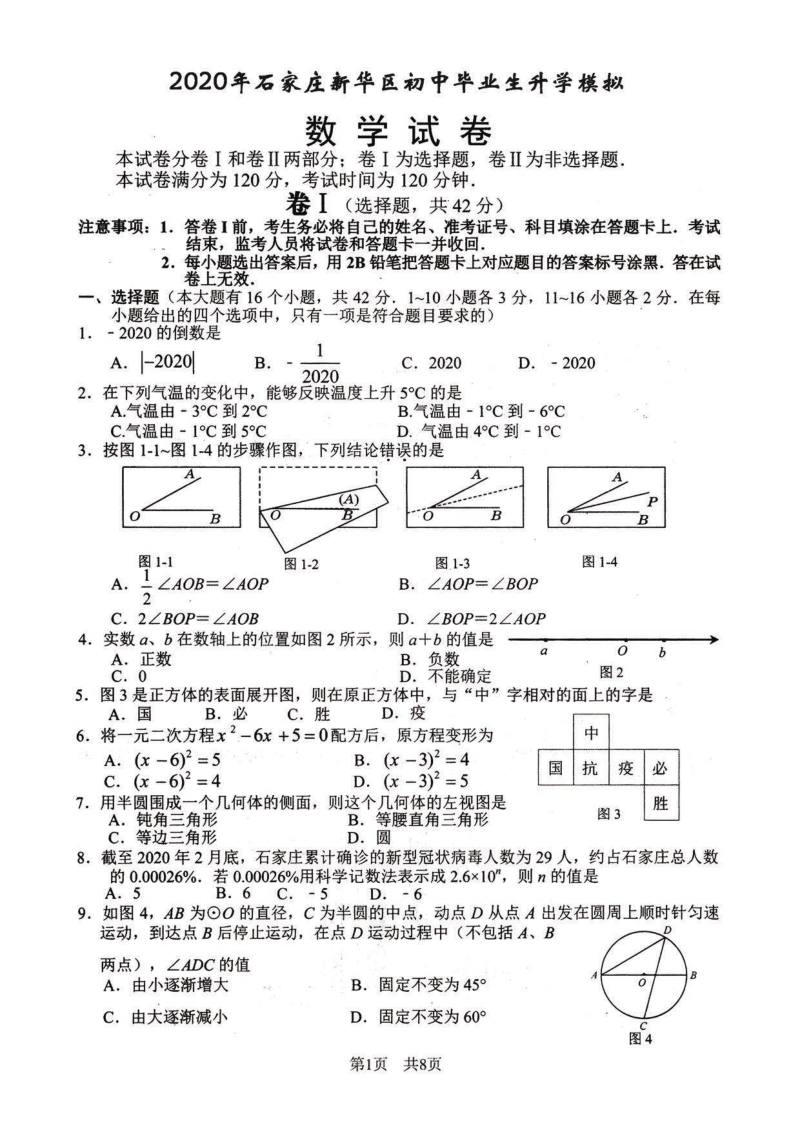
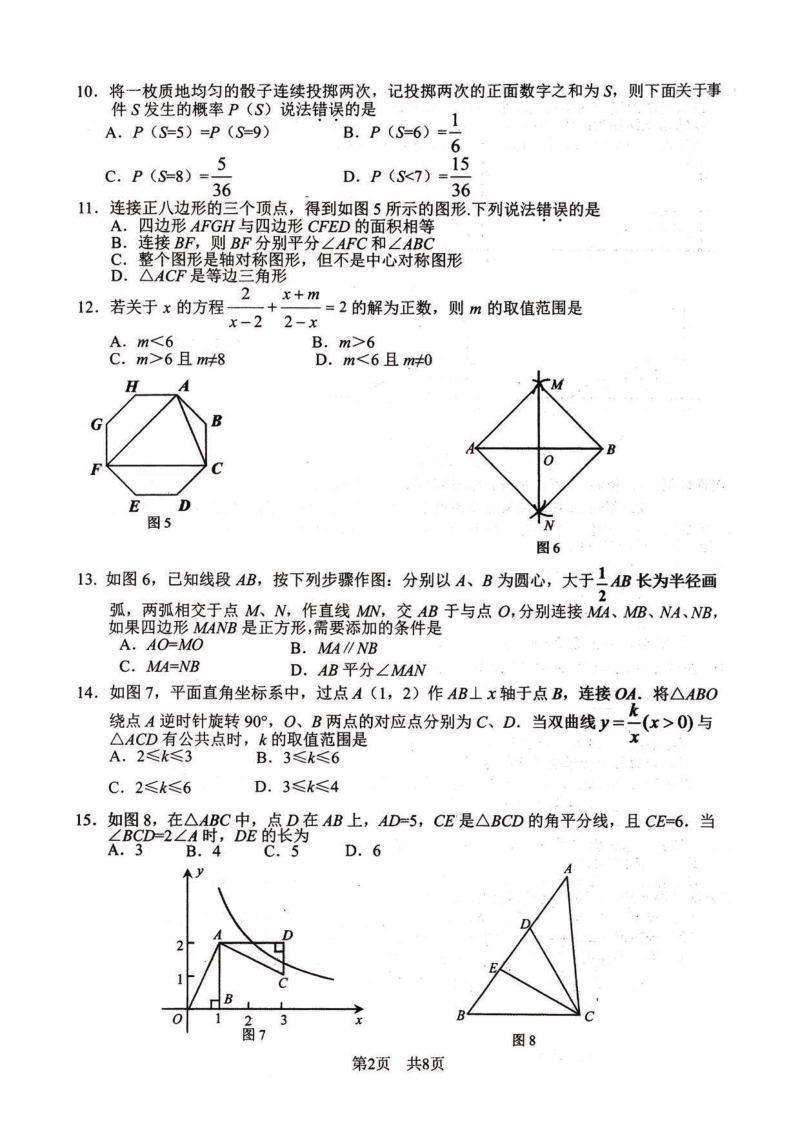
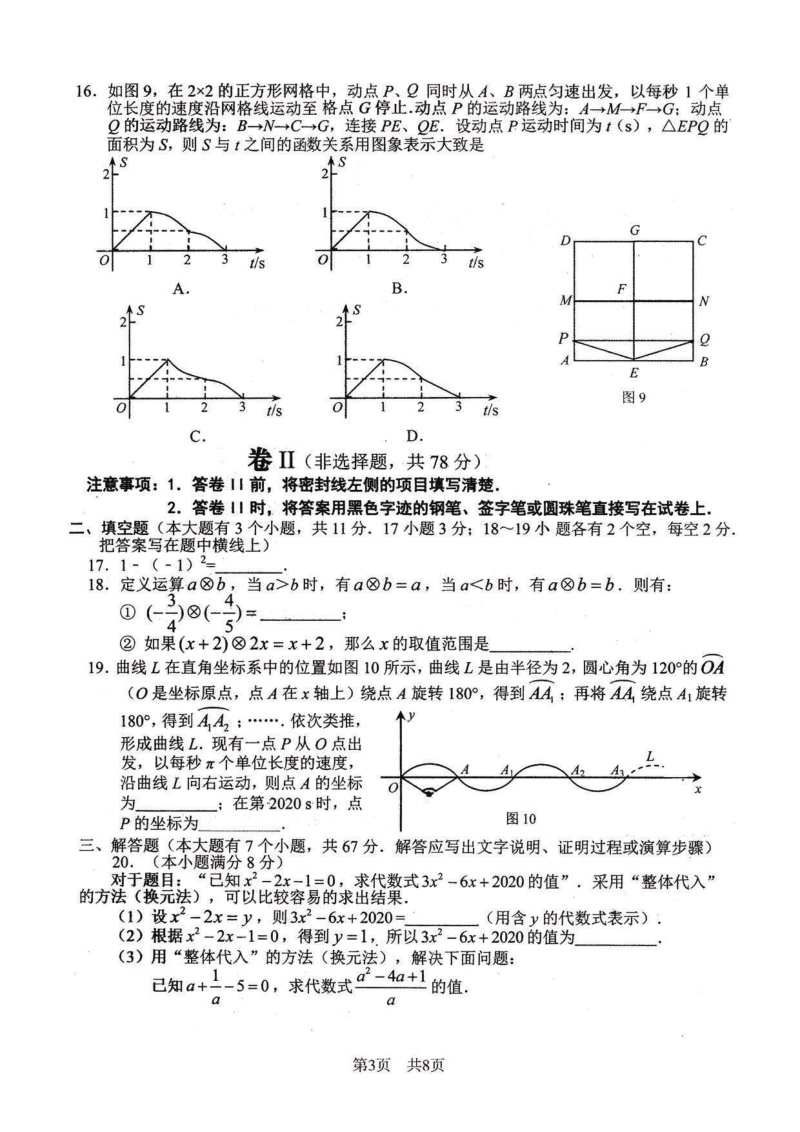
1、 数学模拟试题参考答案及评分标准第 1页（共 4 页） 2020 年新华区初中毕业生升学模拟 数学试题参考答案及评分标准 说明： 1在阅卷过程中，如考生还有其它正确解法，可参照评分标准按步骤酌情给分 2坚持每题评阅到底的原则，当考生的解答在某一步出现错误，影响了后继部分时， 如果该步以后的解答未改变这一题的内容和难度，可视影响的程度决定后面部分的 给分，但不得超过后继部分应给分数的一半；如果这一步后面的解答有较严重的错 误，就不给分 3解答右端所注分数，表示正确做到这一步应得的累加分数只给整数分数 一、选择题（本大题有 16 个小题，共 42 分110 小题各 3 分，1116 小题各 2 分
2、） 题号12345678 答案BADBCBCD 题号910111213141516 答案BBDDACBA 二、填空题（本大题有 3 个小题，共 11 分17 小题 3 分；1819 小题各有 2 个空，每空 2 分） 170；18 3 4 ，x2；19 （2 3，0） ，（3030 3，0） 三、解答题（本大题共 7 个小题；共 67 分） 20 （1）答：32020y ； 2 分 （2）2023； 2 分 （3）解：设 1 ab a ，则 2 411 44 aa ab aa 6 分 1 50a a ， 50b，解得：b=5 2 41 4541 aa b a 8 分 21解： （1）35342
3、34； 2 分 （2）猜想：第 n 个等式为：3n+13n23n3 分 理由如下： 3n+13n33n3n（31）3n23n， 3n+13n23n；6 分 （3）根据发现的规律，有：3113102310， 数学模拟试题参考答案及评分标准第 2页（共 4 页） （3231）+（3332）+（3433）+（311310）2（31+32+33+310） ， 311312（31+32+33+310） ， 即 31+32+33+310 2 1 (3113） 8 分 311177147， 31+32+33+310 2 1 (1771473）88572 9 分 22解： （1）填表（自左向右，从上到下的顺序
4、）：8.5，8.5，8，1.64 分 （2）小明在初中队5 分 理由：根据（1）可知，初中、高中队的中位数分别为 8.5 分和 8 分， 88.5，小明在初中队7 分 （3）初中队的成绩好些因为两个队的平均数相同，初中队的中位数高，而且初中队的 方差小于高中队的方差，所以在平均数相同的情况下中位数高、方差小的初中队成 绩较好9 分 23（1）证明：根据旋转的性质，知：EAC2， BAC， BAEEACBAC2， BAEBAC2 分 AEAC，ABAB， ABEABC 3 分 BEBC4 分 （2）答：四边形 ABED 是菱形5 分 理由如下： 根据旋转的性质，知：AD=AB，DEBC， AB=
5、BC，BEBC， AD=AB=BEDE 四边形 ABED 是菱形 7 分 （3） 30 609 分 24解： （1）甲车的速度为 100 km/h， S甲与 t 之间的函数关系式为 S甲=100t1 分 两车匀速行驶，设 S乙与 t 之间的函数关系式为 S乙= kt+b， 又当 t=2 h 时，S乙=560 km；当 t=5 h 时，S乙=320 km， 5602, 3205. kb kb 解得 80, 720. k b 数学模拟试题参考答案及评分标准第 3页（共 4 页） S乙与 t 之间的函数关系式为 S乙=80t+720 3 分 （3）当两车相遇时，有 S甲=S乙， 即 100t =80
6、t+720， 解得 t =45 分 （2） 在两车相遇之前，即当 t4 时， 有 S乙S甲，S乙S甲180 即（80t+720）100t180，180t540解得 t3 3t47 分 在两车相遇之后，即当 t4 时， 有 S甲S乙，S甲S乙180 即 100t（80t+720）180解得 t5 4t59 分 综上可知：当两车距离小于 180 km 时，3ht5h10 分 25. 解： （1）在RtABC中，AB=10，BC=6， 2222 1068ACABBC， 点O为AC边的中点， 11 84 22 AOAC 2 分 ODAB，ACB=90，ADO=ACB， 又A=A，AODABC ODAO
7、 BCAB ，即 4 610 x ， 12 5 x 4 分 （2） 点O与点C重合，ODAB=ACBC，即 10x=86， 24 5 x 5 分 过点D作DHAC，垂足为H，则有DHO=ACB=90 易得：DOH=ABC，DOHABC DHOHDO ACBCAB ，即 24 5 8610 DHOH ， 96 25 DH ， 72 25 OH 7 分 数学模拟试题参考答案及评分标准第 4页（共 4 页） OF=OD= 24 5 ，FH=OH+OF=192 25 在RtDFH中，根据勾股定理，得： 2222 9619296 ()()5 252525 DFDHFH8 分 （3）0x3 或 x12 1
8、0 分 26解： （1）b=c1（或是这个等式的其他变形） 2 分 （2）OB=OC3 分 理由如下： 抛物线 L： 2 yxbxc 过点 B（m，0） （m0） ，点 C， OB=m，OC=c，且 2 0mbmc ，即 2 0mbmc 由（1）知：b=c1，代入上式，得： 2 (1)0mcmc ，即 2 (1)mcmm m0，c=m OB=OC5 分 （3） 当 m3 时，得： 930, 1. bc cb 解得： 2, 3. b c 2 23yxx 6 分 OB=OC=3，A（1，0） ，AB=4 11 4 36 22 ABC SAB OC 连接 OP（如图 1 所示） ，则有： 1113 333 3(3) 2222 PBCPOCPOBOBC SSSSxyxy 点 P（x，y）在抛物线 L 上， 2 23yxx 2 3 (3 ) 2 PBC Sxx ， SPBC 1 2 SABC， A x L B 图 1 O C 1 y P 数学模拟试题参考答案及评分标准第 5页（共 4 页） 2 31 (3 )6 22 xx， 即 2 320xx，8 分 解得：x1=1，x2=2 当 x=1 时， 2 12 134y ；当 x=2 时， 2 22233y 点 P 的坐标为（1，4）或（2，3）10 分 15 或3 12 分
