 七年级下册数学期末培优题汇总
七年级下册数学期末培优题汇总
《七年级下册数学期末培优题汇总》由会员分享,可在线阅读,更多相关《七年级下册数学期末培优题汇总(42页珍藏版)》请在七七文库上搜索。
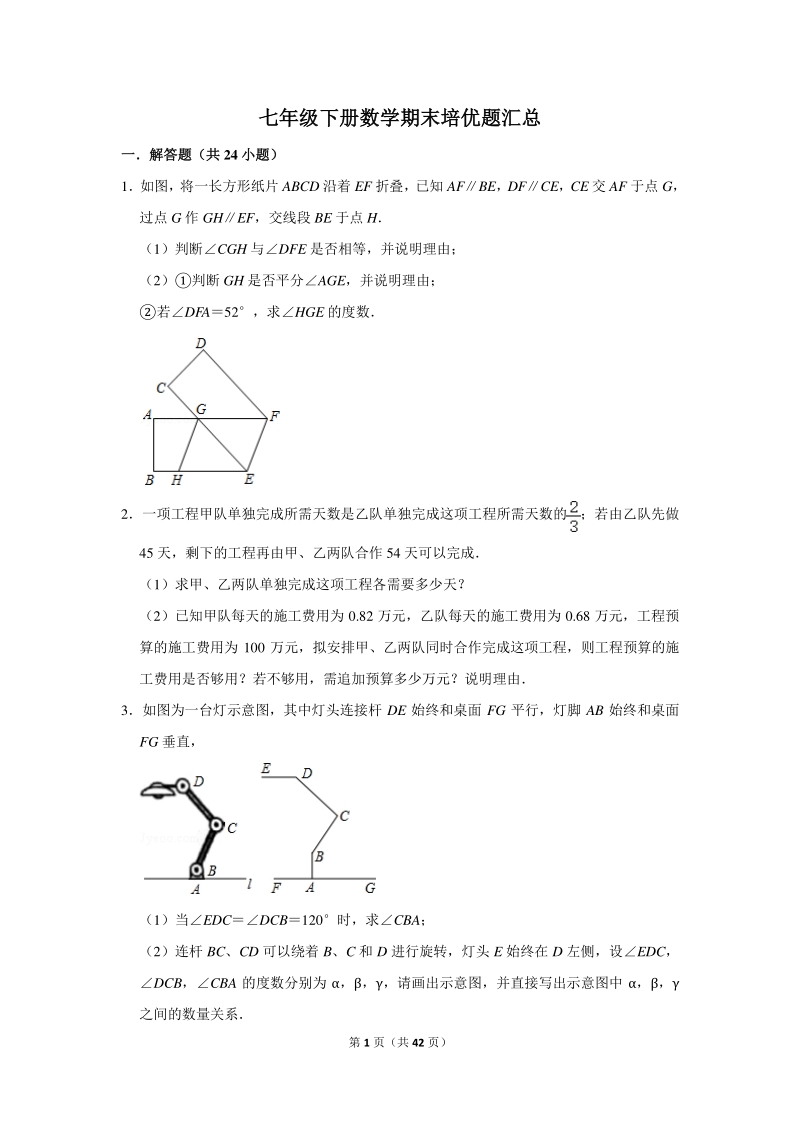
1、 第 1 页(共 42 页) 七年级下册数学期末培优题汇总七年级下册数学期末培优题汇总 一解答题(共一解答题(共 24 小题)小题) 1如图,将一长方形纸片 ABCD 沿着 EF 折叠,已知 AFBE,DFCE,CE 交 AF 于点 G, 过点 G 作 GHEF,交线段 BE 于点 H (1)判断CGH 与DFE 是否相等,并说明理由; (2)判断 GH 是否平分AGE,并说明理由; 若DFA52,求HGE 的度数 2一项工程甲队单独完成所需天数是乙队单独完成这项工程所需天数的;若由乙队先做 45 天,剩下的工程再由甲、乙两队合作 54 天可以完成 (1)求甲、乙两队单独完成这项工程各需要多少
2、天? (2)已知甲队每天的施工费用为 0.82 万元,乙队每天的施工费用为 0.68 万元,工程预 算的施工费用为 100 万元,拟安排甲、乙两队同时合作完成这项工程,则工程预算的施 工费用是否够用?若不够用,需追加预算多少万元?说明理由 3如图为一台灯示意图,其中灯头连接杆 DE 始终和桌面 FG 平行,灯脚 AB 始终和桌面 FG 垂直, (1)当EDCDCB120时,求CBA; (2)连杆 BC、CD 可以绕着 B、C 和 D 进行旋转,灯头 E 始终在 D 左侧,设EDC, DCB,CBA 的度数分别为 ,请画出示意图,并直接写出示意图中 , 之间的数量关系 第 2 页(共 42 页)
3、 4如图,将几个小正方形与小长方形拼成一个边长为(a+b+c)的正方形 (1)若用不同的方法计算这个边长为(a+b+c)的正方形面积,就可以得到一个等式, 这个等式可以为 (只要写出一个即可) ; (2)请利用(1)中的等式解答下列问题: 若三个实数 a,b,c 满足 a+b+c11,ab+bc+ac38,求 a2+b2+c2的值; 若三个实数 x,y,z 满足 2x4y8z,x2+4y2+9z244,求 2xy3xz6yz 的值 5阅读下列材料: 对于多项式 x2+x2,如果我们把 x1 代入此多项式,发现 x2+x2 的值为 0,这时可以 确定多项式中有因式(x1) ;同理,可以确定多项式
4、中有另一个因式(x+2) ,于是我们 可以得到:x2+x2(x1) (x+2) 又如:对于多项式 2x23x2,发现当 x2 时,2x23x2 的值为 0,则多项式 2x2 3x2 有一个因式(x2) ,我们可以设 2x23x2(x2) (mx+n) ,解得 m2,n 1,于是我们可以得到:2x23x2(x2) (2x+1) 请你根据以上材料,解答以下问题: (1) 当 x 时, 多项式 6x2x5 的值为 0, 所以多项式 6x2x5 有因式 , 从而因式分解 6x2x5 ; (2)以上这种因式分解的方法叫试根法,常用来分解一些比较复杂的多项式,请你尝试 用试根法分解多项式: 2x2+5x+
5、3; x37x+6; (3)小聪用试根法成功解决了以上多项式的因式分解,于是他猜想: 代数式(x2)3(y2)3(xy)3有因式 , , , 所以分解因式(x2)3(y2)3(xy)3 6对于一个图形,通过两种不同的方法计算它们的面积,可以得到一个数学等式,例如图 第 3 页(共 42 页) 1 可以得到(a+b)2a2+2ab+b2,请解答下列问题: (1)类似图 1 的数学等式,写出图 2 表示的数学等式; (2)若 a+b+c10,ab+ac+bc35,用上面得到的数学等式乘 a2+b2+c2的值; (3) 小明同学用图 3 中的 x 张边长为 a 的正方形, y 张边长为 b 的正方形
6、, z 张边长为 a、 b 的长方形拼出一个面积为(a+7b) (9a+4b)的长方形,求(x+y+z)的值 7如图,ADEC (1)若C40,AB 平分DAC,求DAB 的度数 (2)若 AE 平分DAB,BF 平分ABC,试说明 AEBF 的理由 8已知关于 x,y 的二元一次方(a 为实数) (1)若方程组的解始终满足 ya+1,求 a 的值; (2)已知方程组的解也是方程 bx+3y1(b 为实数,b0 且 b6)的解 探究实数 a,b 满足的关系式; 若 a,b 都是整数,求 b 的最大值和最小值 9李师傅要给一块长 9 米,宽 7 米的长方形地面铺瓷砖,如图,现有 A 和 B 两种
7、款式的瓷 砖,且 A 款正方形瓷砖的边长与 B 款长方形瓷砖的长相等,B 款瓷砖的长大于宽,已知 一块 A 款瓷砖和一块 B 款瓷砖的价格和为 140 元;3 块 A 款瓷砖价格和 4 块 B 款瓷砖价 格相等请回答以下问题: (1)分别求出每款瓷砖的单价; (2)若李师傅买两种瓷砖共花了 1000 元,且 A 款瓷砖的数量比 B 款多,则两种瓷砖各 买了多少? (3)李师傅打算按如下设计图的规律进行铺瓷砖,若 A 款瓷砖的用量比 B 款瓷砖的 2 倍少 14 块, 且恰好铺满地面, 则 B 款瓷砖的长和宽分别为 米 (直接写出答案) ? 第 4 页(共 42 页) 10已知,直线 ABDC,
8、点 P 为平面上一点,连接 AP 与 CP (1)如图 1,点 P 在直线 AB、CD 之间,当BAP60,DCP20时,求APC (2)如图 2,点 P 在直线 AB、CD 之间,BAP 与DCP 的角平分线相交于点 K,写出 AKC 与APC 之间的数量关系,并说明理由 (3)如图 3,点 P 落在 CD 外,BAP 与DCP 的角平分线相交于点 K,AKC 与 APC 有何数量关系?并说明理由 11某校七年级为了表彰“数学素养水平测试”中表现优秀的同学,准备用 480 元钱购进笔 记本作为奖品若 A 种笔记本买 20 本,B 本笔记本买 30 本,则钱还缺 40 元;若 A 种笔 记本买
9、 30 本,B 种笔记本买 20 本,则钱恰好用完 (1)求 A,B 两种笔记本的单价; (2)由于实际需要,需要增加购买单价为 6 元的 C 种笔记本若干本若购买 A,B,C 三种笔记本共 60 本,钱恰好全部用完,任意两种笔记本之间的数量相差小于 15 本,则 C 种笔记本购买了 本 (直接写出答案) 12如图 1,ABCD,定点 E,F 分别在定直线 AB,CD 上,点 A 在点 B 左侧,点 C 在点 D 左侧,动点 P 不在直线 AB,CD,EF 上 (1) 【初步探究】试问当动点 P 位于两平行线 AB,CD 之间时,如图 2,图 3,AEP, 第 5 页(共 42 页) EPF,
10、PFC 满足怎样的数量关系?并说明相应理由 (2) 【深入探究】当点 P 在不同的位置时,请画出AEP,EPF,PFC 三个角中其 中个角度数等于另两个角的度数之和时的所有示意图,并直接写出相应关系式,第(1) 小题的关系式除外 13通过对某校营养午餐的检测,得到如下信息:每份营养午餐的总质量 400g;午餐的成 分为蛋白质、碳水化合物、脂肪和矿物质,其组成成分所占比例如图 1 所示;其中矿物 质的含量是脂肪含量的 1.5 倍,蛋白质和碳水化合物含量占 80% 某校营养午餐组成成分统计图某校营养午餐组成统计图 (1)设其中蛋白质含量是 x(g) 脂肪含量是 y(g) ,请用含 x 或 y 的代
11、数式分别表示 碳水化合物和矿物 质的质量 (2)求每份营养午餐中蛋白质、碳水化合物、脂肪和矿物质的质量 (3)参考图 1,请在图 2 中完成这四种不同成分所占百分比的扇形统计图 14某校举办“迎亚运“学生书画展览,现要在长方形展厅中划出 3 个形状、大小完全一样 的小长方形(图中阴影部分)区域摆放作品 (1)如图 1,若大长方形的长和宽分别为 45 米和 30 米,求小长方形的长和宽 (2)如图 2,若大长方形的长和宽分别为 a 和 b 直接写出 1 个小长方形周长与大长方形周长之比; 若作品展览区域(阴影部分)面积占展厅面积的,试求的值 15 (1)已知ABC,射线 EDAB,如图 1,过点
12、 E 作DEFABC,说明 BCEF 的 第 6 页(共 42 页) 理由 (2)如图 2,已知ABC,射线 EDAB,ABC+DEF180判断直线 BC 与直线 EF 的位置关系,并说明理由 (3)根据以上探究,你发现了一个什么结论?请你写出来 (4)如图 3,已知 ACBC,CDAB,DEAC,HFAB,若148,试求2 的 度数 16教科书中这样写道: “我们把多项式 a2+2ab+b2及 a22ab+b2叫做完全平方式” ,如果 一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现 完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法配方法是一 种重
13、要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能 解决一些与非负数有关的问题或求代数式最大值,最小值等 例如:分解因式 x2+2x3(x2+2x+1)4(x+1) 24(x+1+2) (x+12)(x+3) (x1) ; 例如求代数式 2x2+4x6 的最小值.2x2+4x62 (x2+2x3) 2 (x+1) 28 可 知当 x1 时,2x2+4x6 有最小值,最小值是8,根据阅读材料用配方法解决下列问 题: (1)分解因式:m24m5 (2)当 a,b 为何值时,多项式 a2+b24a+6b+18 有最小值,并求出这个最小值 (3)当 a,b 为何值时,多项式 a2
14、2ab+2b22a4b+27 有最小值,并求出这个最小值 17商家常将两种糖混合成“什锦糖”出售对“什锦糖”的定价用以下方法确定: 若 A 种糖的单价为 a 元/千克,B 种糖的单价为 b 元/千克(ab) ,则 m 千克的 A 种糖与 n 千克的 B 种糖混合而成的“什锦糖”单价为元 (1)当 a20,b30 时, 将 10 千克的 A 种糖与 15 千克的 B 种糖混合而成的“什锦糖”单价为多少? 第 7 页(共 42 页) 在的基础上,若要将“什锦糖”单价提高 2 元,则需增加 B 种糖多少千克? (2)若现有两种“什锦糖” :一种是由 10 千克的 A 种糖和 10 千克的 B 种糖混
15、合而成, 另一种是由 100 元价值的 A 种糖和 100 元价值的 B 种糖混合而成,则这两种“什锦糖” 的单价哪一种更大? 18如图,在长方形 ABCD 中,在边 AB,BC 上分别取点 E,F,使得 BE3AE,CF2BF, CE 与 DF 交于点 O,设 ABa,BCb,三角形 FOC 的面积为 x (1)请用含 a,b,x 的代数式表示三角形 COD 的面积; (2)连结 OA,OB,若三角形 AOB 的面积为 10,三角形 COD 的面积为 8 时,求长方形 ABCD 的面积; (3)当 AB4,BC9 时,求 x 的值 19如图 1,已知两条直线 AB,CD 被直线 EF 所截,
16、分别交于点 E,点 F,EM 平分AEF 交 CD 于点 M,且FEMFME (1)判断直线 AB 与直线 CD 是否平行,并说明理由; (2)如图 2,点 G 是射线 MD 上一动点(不与点 M,F 重合) ,EH 平分FEG 交 CD 于 点 H,过点 H 作 HNEM 于点 N,设EHN,EGF 当点 G 在点 F 的右侧时,若 50,求 的度数; 当点 G 在运动过程中, 和 之间有怎样的数量关系?请写出你的猜想, 并加以证明 20某市为创建生态文明建设城市,对公路旁的绿化带进行全面改造现有甲、乙两个工程 队,甲队单独完成这项工程,刚好如期完成,每施工一天,需付工程款 1.5 万元;乙
17、工程 队单独完成这项工程要比规定工期多用 a 天, 乙工程队每施工一天需付工程款 1 万元 若 第 8 页(共 42 页) 先由甲、乙两队一起合作 b 天,剩下的工程由乙队单独做,也正好如期完工 (1)当 a6,b4 时,求工程预定工期的天数 (2)若 ab2a 是偶数 求甲队、乙队单独完成工期的天数(用含 a 的代数式表示) 工程领导小组有三种施工方案: 方案一:甲队单独完成这项工程; 方案二:乙队单独完成这项工程; 方案三:先由甲、乙两队一起合作 b 天,剩下的工程由乙队单独做 为了节省工程款,同时又能如期完工,请你选择一种方案,并说明理由 21 为节约用水, 某市居民生活用水按阶梯式计算
18、, 水价分为三个阶梯, 价格表如下表所示: (注:居民生活用水水价供水价格+污水处理费)某市自来水销售价格表 类别 月用水量(立方米) 供水价格 污水处理 费(元/立 方米) 备注 居民生活 用水 阶梯一 018(含 18) 1.90 1.00 每户产生的污水量等 于该户用水量 阶梯二 1825 (含 25) a 阶梯三 25 以上 b (1)当居民月用水量在 18 立方米及以下时,水价是 元/立方米; (2)小明家 2 月份用水量为 20 立方米,付水费 59.90 元.4 月份用水量为 33 立方米,付 水费 132.75 元求 a,b 的值; (3)小明家 5 月份交水费 112.65
19、元,试求小明家该月的用水量 22我们发现:, (1)利用上述发现计算:+ (2)现有咸度较低的盐水 a 克,其中含盐 b 克,若再往该盐水中加 m 克盐(加入的盐均 能溶解) ,生活经验告诉我们盐水会更咸 请你用两个代数式的大小关系来表达这一现象,并通过分式运算说明结论的正确性; 第 9 页(共 42 页) 应用上述原理说明对于任意正整数 n,算式+ +的值都小于 23已知:ABC 和同一平面内的点 P (1)如图 1,若点 P 在 BC 边上过点 P 作 PEAB 交 AC 于点 E,作 PFAC 交 AB 于点 F根据题意,请在图 1 中补全图形,并直接写出A 与EPF 的数量关系; (2
20、)如图 2,若点 P 在 CB 的延长线上,且 PFAC,AEPF请判断 AB 与 PE 的位置关系并说明理由; (3)如图 3,点 P 是ABC 外部的一点,过点 P 作 PEAB 交直线 AC 于点 E,作 PF AC 交直线 AB 于点 F,请直接写出A 与EPF 的数量关系,并图 3 中补全图形 24 某工程队用甲、 乙两台隧道挖掘机从两个方向挖掘同一条隧道, 因为地质条件不同, 甲、 乙的挖掘速度不同,已知甲、乙同时挖掘 3 天,可以挖 216 米,若甲挖 2 天,乙挖 5 天 可以挖掘 270 米 (1)请问甲、乙挖掘机每天可以挖掘多少米? (2)若乙挖掘机比甲挖掘每小时多挖掘 1
21、 米,甲、乙每天挖掘的时间相同,求甲每小时 挖掘多少米? (3)若隧道的总长为 a 米,甲、乙挖掘机工作 b 天后,因为甲挖掘机进行设备更新,乙 挖掘机设备老化,甲比原来每天多挖 m 米,同时乙比原来少挖 m 米(m10) 最终,甲、 乙两台挖掘机在相同时间里各完成隧道总长的一半,请用含 m,b 的代数式表示 a 第 10 页(共 42 页) 七年级下册数学期末培优题汇总七年级下册数学期末培优题汇总 参考答案与试题解析参考答案与试题解析 一解答题(共一解答题(共 24 小题)小题) 1如图,将一长方形纸片 ABCD 沿着 EF 折叠,已知 AFBE,DFCE,CE 交 AF 于点 G, 过点
22、G 作 GHEF,交线段 BE 于点 H (1)判断CGH 与DFE 是否相等,并说明理由; (2)判断 GH 是否平分AGE,并说明理由; 若DFA52,求HGE 的度数 【分析】 (1)由四边形 ABCD 是矩形,得到 ADBC,得到 CGDF 根据平行线的性质 得到AGCAFD,AGHAFE,于是得到CGHDFE; (2)根据平行线的性质得到AGHGHE,且GHEHGE,求得AGH HGE,根据角平分线的定义即可得到结论; 由折叠的性质得到EFG1,根据平行线的性质和平角的定义即可得到结论 【解答】解: (1)CGHDFE, 理由:四边形 ABCD 是矩形, ADBC, CGDF,GHE


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 全册
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-140756.html